Проникновение внутренних гравитационных волноводных мод в верхнюю атмосферу

Настоящая работа посвящена исследованию свойств захваченных атмосферных мод, простирающихся на большие высоты. Описание таких мод может быть получено с помощью диссипативного решения над источником (ДРНИ) [Руденко, Дмитриенко, 2015]. Действительно, ДРНИ удовлетворяет верхнему граничному условию для захваченных мод — непоступлению энергии сверху, а так как источник в задаче о захваченных модах отсутствует, ДРНИ справедливо во всей атмосфере. ДРНИ может принимать на поверхности Земли, вообще говоря, произвольные значения. Таким образом, задача поиска решений для захваченных мод сводится к задаче выбора ДРНИ, удовлетворяющих нижнему граничному условию для захваченных мод — нулевой вертикальной скорости на поверхности Земли; это граничное условие определяет дисперсионное уравнение для захваченных мод.

Мы рассматриваем ВГВ-моды волновода, создаваемого температурной стратификацией нижней атмосферы. Такие моды даже без учета атмосферной диссипации не могут описываться решениями с действительными собственными значениями вследствие подбарьерного просачивания из волновода.

Так что, строго говоря, рассматриваемые захваченные моды являются не отдельными дискретными модами, а коллективными. Однако с точки зрения нашей задачи это обстоятельство существенно только тем, что мы должны строить решение над источником с комплексными частотой или волновым числом — в отличие от [Руденко, Дмитриенко, 2015], где для расчетов использовались действительные параметры частоты и волнового числа. Мы в настоящей работе полагаем заданной действительную частоту и находим соответствующее ей комплексное горизонтальное волновое число, при котором ДРНИ удовлетворяет нижнему граничному условию. Такое ДРНИ и представляет собой волноводную моду. Согласно [Руденко, Дмитриенко, 2015], ДРНИ образуется посредством соединения трех решений: аналитического решения для верхней части атмосферы ( R ^I ), рассматриваемой в рамках изотермического приближения и численных решений для реальной неизотермической диссипативной атмосферы в средней части ( R ^II ) и для реальной неизотермической в рамках приближения малой диссипации в нижней части ( R ^III ). Таким образом, получаемые для волноводных мод решения дают связь их амплитуды и других параметров в нижней атмосфере с их параметрами в верхней изотермической атмосфере.

Возможность описания амплитудных характеристик волноводных мод на больших высотах является крайне важной, прежде всего с точки зрения их экспериментального обнаружения. Несмотря на то что энергия волноводных мод в основном сосредоточена на низких высотах в области их захвата, в силу экспоненциального роста относительных величин возмущений, связанного с падением атмосферной плотности, мы имеем лишь опосредованную возможность их наблюдения преимущественно в верхней части атмосферы. В этой области относительные значения возмущенных величин велики по сравнению с их значениями в нижней части атмосферы и на тех высотах, где возмущения еще не совсем подавлены диссипацией, они могут приводить к значительным возмущениям заряженной компоненты ионосферы. Именно благодаря «невидимому» распространению ВГВ внизу мы наблюдаем весьма распространенное явление перемещающихся ионосферных возмущений (ПИВ).

Работа организована следующим образом. В секции 1 описана применяемая для расчетов модель атмосферы. Секция 2 посвящена построению и анализу волноводных мод спектрального диапазона ВГВ. Мы сравниваем решения волноводной задачи, построенные с помощью ДРНИ, с решениями для бездиссипативного приближения, полученными как ВKБ-методом, так и численными методами. Такие сравнения преследуют сразу две цели. Во-первых, они позволяют достичь ясности в понимании влияния диссипации на основные характеристики волноводного распространения: дисперсионные соотношения, волноводное просачивание и горизонтальное затухание волноводных мод. Во-вторых, они являются дополнительными тестами к тестам [Руденко, Дмитриенко, 2015] как метода получения ДРНИ, так и соответствующих кодов. Мы получаем дисперсионные свойства и полное описание высотной структуры всех компонент возмущения. В полученном волноводном решении присутствуют все характерные особенности захваченных ВГВ в реальной атмосфере: локализация вследствие температурной стратификации; просачивание через область непрозрачности; качественные изменения волновой структуры, связанные с диссипативным характером распространения возмущения в верхней атмосфере. Мы получаем полную информацию о всей высотной структуре волноводных мод, которая непосредственно может быть использована для установления количественного соответствия ВГВ-мод с ПИВ. Мы показываем, что наши волноводные решения хорошо согласуются с основными характеристиками ПИВ, следующими из наблюдений: соотношениями периодов с пространственными масштабами, горизонтальным затуханием, величинами полной фазовой скорости распространения, наклонами фазовых фронтов.

Следует отметить, что волноводные моды исследовались в давних работах [Francis, 1973a, b] и их результаты широко используются и в теоретических работах, и в интерпретации наблюдений различных возмущений, в том числе и в верхней атмосфере [Shibata, Okuzawa, 1983; Afraimovich et al., 2001;

Vadas, Liu, 2009; Vadas, Nicolls, 2012; Idrus et al., 2013; Heale et al., 2014; Hedlin, Drob, 2014 и др.]. В работах [Francis, 1973a, b] были получены дисперсионные характеристики и вертикальные структуры волноводных мод. В работе [Francis, 1973b] было показано, что одна или две нижние ВГВ-моды способны за счет волноводного просачивания присутствовать на ионосферных высотах. Метод Фрэнсиса может рассчитывать достаточно хорошо структуру волновых возмущений в нижней части атмосферы и дисперсионные характеристики захваченных неоднородностями нижней атмосферы мод. Детально метод Фрэнсиса с точки зрения его применимости в верхней атмосфере обсужден в [Руденко, Дмитриенко, 2015]. Здесь мы отметим только то обстоятельство, что особенности метода Фрэнсиса, состоящие в использовании всюду понижения порядка дифференциальных уравнений, допустимого только при слабой диссипации, в действительности не позволяют получить правильного описания возмущений в верхней атмосфере. В отличие от метода Фрэнсиса в нашем методе построения ДРНИ мы используем понижение порядка волновых уравнений до второго (в собственном варианте) только для области высот малой диссипации, где это вполне оправданно. Поэтому наш метод, в отличие от метода Фрэнсиса, позволяет адекватно описывать верхнеатмосферные возмущения.

1.    МОДЕЛЬ АТМОСФЕРЫ

Наши вычисления мы проводим на модели атмосферы, задаваемой высотным профилем невозмущенной температуры Т ₀( z ) согласно распределению NRLMSISE-2000 с географическими координатами Иркутска для местного полудня зимнего солнцестояния:

gz 1 -----dz po(z) = po(O)e Rj0 T0(z') , po(O) = 1.01 Па;

- g J z —1— dz'

P o ( z ) = P o (0) e R ⁰ T ⁰⁽ z )   , P o (O) = 287.0 г/м ³ .

Здесь p 0 , ρ 0 — невозмущенные величины давления и плотности; z — вертикальная координата, отсчитываемая от поверхности Земли; g =9.807 м/с ² — ускорение свободного падения, R =287 Дж/(кг ·K ) — универсальная газовая постоянная. Мы учитываем, что атмосфера обладает теплопроводностью, полагая ее динамический коэффициент постоянным.

Поскольку для нашего метода построения волновых решений кроме распределения невозмущенной температуры необходимы также ее первая, вторая и третья производные (см. [Руденко, Дмитриенко, 2015]), мы используем в качестве модели для расчетов аппроксимацию модели NRMSIS, обладающую гладкостью вплоть до третьей производной:

T ( z >  430) = 944.4,

(v

T (95.3 <  z <  430) =

f n ( 430 — z Y)1 ³

cos I “  ------------ I

2 ( 430 — 95.3 J

—

1 X

x (944.4 — 185.4) + 944.4,

Лг

T (46 <  z <  95.3) = —

x (257 — 185.4) + 185.4,

T (20 <  z <  46) =

| п | 95.3 — z Y cos I — ---------

2 ( 95.3 — 46 )

—

1 X

Мы используем в настоящей работе те же обозна-

чения, что и в работе [Руденко, Дмитриенко, 2015].

Обсудим приведенный на рис. 2 профиль функции U для произвольно выбранных волновых парамет-

I п [ z — 20 cos I — -------

2 ( 46 — 20

—

1 X

ров ω и

KT

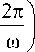
= 90 мин,

'

2 п k _x

= 1390 км.

x (215.1 — 257) = 215.1,

T (0 <  z <  20) =

cos

— 1 X

Хорошо видно, что волноводная локализация возможна в области распространения ниже высоты z 1 за счет верхней запирающей стенки, создаваемой отрицательными значениями U в области z 1 < z < z 2 . Выше z ₂ начинается область свободного распро-

x (215.1 — 270.1) + 215.1.

Исходная зависимость Т 0 ( z ) и ее аппроксимация представлены на рис. 1.

При выборе модели для зимнего периода мы ориентировались на то, что наши результаты в наибольшей степени можно сравнить с имеющимися конкретными наблюдениями для нашего региона во время наиболее уверенного приема ПИВ. В летний период у нас они практически не наблюдаются. Этому могут быть две причины: либо источники возмущений себя не проявляют, либо для этого периода нарушаются условия волноводного запирания по предполагаемым трассам распространения. Для предметного обсуждения таких факторов необходим отдельный анализ возможных трасс волноводного распространения при различных положениях источников и пунктов приема.

• 2.    ВГВ-ВОЛНОВОД

  В данной секции мы рассмотрим низкочастотные ВГВ-возмущения, проявляющиеся на ионосферных высотах вдали от порождающих их источников. Поскольку такие волны не могут захватываться в верхней атмосфере (приближенно изотермической), остается только возможность их интерпретации как возмущений, просачивающихся из ВГВ-волновода, имеющего место на более низких высотах [Hines, 1960].

• 3.1.    Уравнения для волноводной задачи

Мы далее сравниваем три способа решения волноводной задачи: 1) ВКБ-описание без учета диссипации; 2) численное решение краевой задачи без учета диссипации; 3) решение волноводной задачи с использованием ДРНИ [Руденко, Дмитриенко, 2015]. Сначала приведем необходимые формулы для каждого из методов.

• 1. ВКБ-приближение без учета диссипации

  Из системы уравнений (7) [Руденко, Дмитриенко, 2015] в главном порядке ВКБ-приближения нетрудно получить квадрат волнового числа в виде

(kzW™ )2 = u (z), где странения в вертикальном направлении, в которую может просачиваться часть энергии волноводной моды. Заметим, что характерной особенностью рассматриваемой задачи является сильная вариация формы и значений U в зависимости от волновых параметров ω и kx. Претерпевают изменения также и значения высот z1 и z2.

Можно показать, что в случае подбарьерного просачивания условие волноводного запирания с просачиванием в ВКБ-приближении может быть представлено модифицированным условием квантования Бора–Зоммерфельда (MBSCQ) с комплексными точками поворота

J^ Uddz

= п

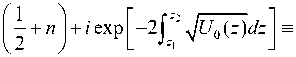
^ п| — + n 1 + iQ , n = 0,1,....

Условие (3) дает дисперсионные соотношения между действительными частотами ω и комплексными волновыми числами kx c малой мнимой частью, отражающей степень горизонтального затухания волноводной моды с номером n. Контур интегрирования C интеграла левой части равенства (3) начинается с нулевой высоты z0 и заканчивается в комплексной точке поворота zc1, близкой к действительной точке поворота z1(U(z1, ω, Rekx)). Кроме того, если существуют внутренние (комплексные) точки поворота, мы полагаем, что контур C также проходит через эти точки (в наших расчетах для простоты участки контура C с ReU(z)<0 не учитываются). Интеграл в аргументе экспоненты в правой части (3) полагаем действительным; индекс 0 функции U в подынтегральном выражении означает, что она является функцией действительной части kx и действительного z: U0(z)=U(z, ω, Rekx). Уравнение (3) решаем методом возмущений. Из уравнения z                (1    ^

Jo Vl ^U 0 ⁽ z )l ^{dz — n}I 2+ n 1 = ^{0                     (4)}

для выбранной действительной ω находим действительный корень k 0 x уравнения (4). Далее вводим обозначения

J_c Uddz

« п

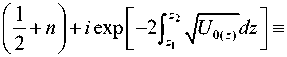
= п|-^ + n 1 + iQ , n = 0,1,...,

U ( z ) = — ¹       + (y — 1) ^k g + ® 2 — k '.

4 cS          cS®   cS kx = k0 x (1 + i 5), U (z) = U0 (z) + k0 xi 5 — U0.     (5)

d k _x

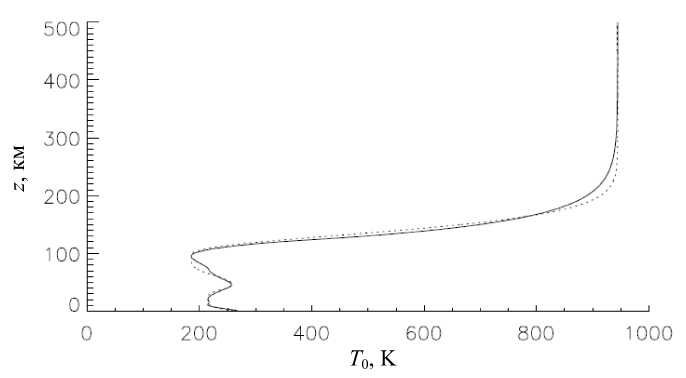
Рис. 1 . Исходное распределение температуры — сплошная линия; аппроксимация — точечная линия

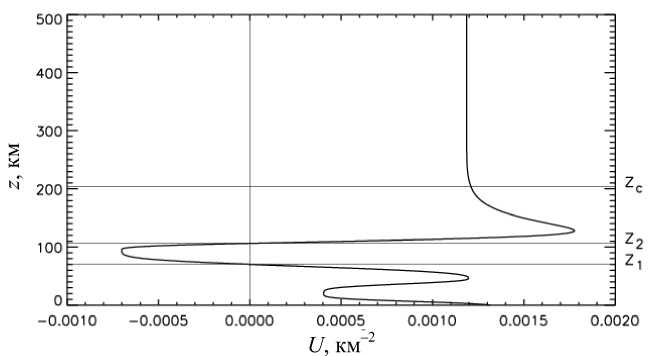
Рис. 2. Характерное высотное распределение функции U

Подставляя (5) в (3) и учитывая комплексность

где

точек поворота z_Cj контура интегрирования интеграла левой части равенства (3), получаем уравнение на комплексную добавку горизонтального вол-

нового вектора:

dz +

q 3/2 ²  3 i п /4/ 3/2V¹

⁵ e^e   k 0 x L j

( d и о / dk x ) ^3/2 |d U _o / dz|

= Q.

-j

p 0                  to N ail =      ; a12 = itop0 I 12

Yp 0

z®rp kk^ \ a21                     +   7 I; a22

P o VY p o g  to JY

Дифференцируем 2-е уравнение из (7):

V ‘= а 21 p' + a 22 -uZ + a2i p + a 22 ^ .

Уравнение (6) на 5 ^1/2 имеет три корня, из которых мы выбираем один, соответствующий затуханию волноводной моды.

2. Краевая задача (BVP, Boundary Value Problem) без учета диссипации

Краевую задачу удобнее всего сформулировать на основе дифференциального уравнения второго

Затем, используя для p ' 1-е уравнение из (7) и выражая p из 2-го уравнения из (7): p = — (ц‘ - a ₂2^z) , получаем уравнение на v_z :

a 21

^ ‘‘+ р^ 2+ в = 0,

^P = ^аи

— ац

- ( ln ^а 21 ) ' =

Т'

T ₀

Y g

порядка на возмущенную вертикальную скорость v_z . Такое уравнение нетрудно получить, используя систему уравнений (2), (9), (10) из работы [Руденко, Дмитриенко, 2015]:

T 0

Г to ²

V к ² c S

—

c s ²

B = — a₂₁a ₁₂ + a_na₂^ + a ₂2 ( ln a^ 1 ) - a 22 =

p ’ = ti_n p + a i^^ ₂ , и ‘ = a_TXp + a ₂₂ u_z,

—

g

c s ²

g

V c s

t ²! g

T 0 J C s

^g c s ²

to

V c S

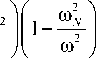
Краевую задачу для уравнения (9) удобно решать с использованием соответствующего нелинейного уравнения Риккати:

G'-PG - BG ² - 1 = 0,                      (10)

где G связана с v_z соотношением

G^ ’z=^ z-                                          (H)

Функция G волноводного решения должна удовлетворять верхнему и нижнему краевым условиям. Вверху ( z = z _∞→+∞) функция G должна соответствовать убегающей вверх волне:

f i / i y1

G⁽z " ) = "[ 2 P ”⁺ V" " 4 ^P " ) '           (12)

В численной реализации высота z _∞ выбиралась равной 430 км, выше которой в нашей модели функция U постоянна. Внизу ( z =0) мы полагаем

G (0)=0.                                     (13)

Это условие, согласно (11), эквивалентно условию равенства нулю функции v_z .

Решая начальную задачу Коши (10), (12) на функцию G, мы определяем значения дисперсионной функции, которая должна удовлетворять условию

D (ω, k x )= G (0, ω, k x )=0.                      (14)

Формально уравнение (14) мы можем решать, полагая действительным либо первый, либо второй аргумент дисперсионной функции D . В первом случае мы будем иметь моды, затухающие (в силу не-эрмитовости задачи) в горизонтальном направлении распространения, во втором — моды, затухающие во времени. В данной работе мы ограничиваемся анализом мод с действительными значениями частоты ω. Вертикальная пространственная структура моды для пары дисперсионных значений ω и k_x , удовлетворяющих уравнению (14), может быть получена путем численного решения задачи Коши на уравнения (9) с начальным условием v z (0)=0, u‘ (0) = 1, соответствующим выбору граничного условия (13) для функции G .

3. Решение волноводной задачи с использованием ДРНИ (BVPD, boundary value problem with dissipation)

Поскольку граничные условия на верхней границе для волноводных мод те же, что и для ДРНИ [Руденко, Дмитриенко, 2015], для решения волноводной задачи достаточно выбрать ДРНИ, удовлетворяющие условию равенства нулю вертикальной скорости на поверхности Земли. Таким образом, соответствующее дисперсионное уравнение принимает вид

D (_to, k x ) = ₄ (0, to , k x ) = 0.                       (15)

Оно является комплексным вследствие просачивания через барьер и наличия диссипации.

3.2.    Численные расчеты характеристик внутренних гравитационных волноводных мод

Прежде всего при расчетах волноводных мод был установлен тот факт, что для частотного диапазона, соответствующего ПИВ на выбранной модели атмосферы, существует только одна безузловая волноводная мода с n=0. Это показали все алгоритмы, описанные в 3.1. Для возможности общего анализа характеристик распространения полученной волноводной моды на одном рис. 3 приводятся:

• •    дисперсионная зависимость горизонтальной длины волны от периода колебаний (сплошная кривая — одинаковая для задач BVPD и BVP; точечная — MBSCQ);

• •    характеристики волны просачивания, формально отнесенные к z = z_c : полная фазовая скорость (штриховая кривая); вертикальная групповая скорость (штрихпунктир); вертикальная длина волны (штрих с тремя точками).

Рисунок 4 представляет характеристики горизонтального затухания 0-моды: BVPD — сплошная кривая; BVP — штриховая кривая; MBSCQ — пунктир.

Отметим наиболее важные моменты:

• •    Рассмотренный случай модельной атмосферы показал существование только одной моды. Поскольку

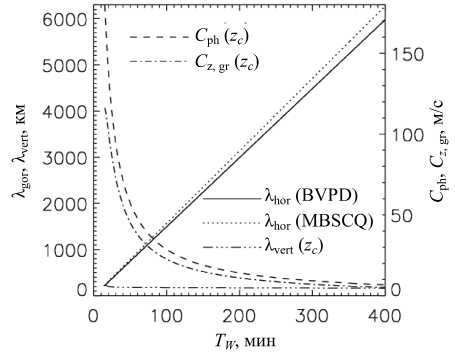
Рис. 3 . Волноводные характеристики 0-моды: горизонтальная длина волны, BVPD=BVP (сплошная кривая); горизонтальная длина волны, MBSCQ (точечная кривая); полная фазовая скорость убегающей волны (штриховая кривая); вертикальная групповая скорость убегающей волны (штрихпунктир); вертикальная длина убегающей волны (штрих с тремя точками)

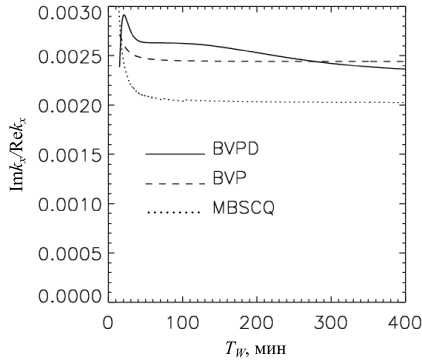
Рис. 4. Горизонтальное затухание 0-моды: BVPD — сплошная кривая; BVP — штриховая кривая; MBSCQ — пунктир

Сравнение теоретических и экспериментальных результатов

	Elevation ( TW =82 мин)	Elevation ( TW =182 мин)	Velocity ( TW =82 мин)	Velocity ( TW =182 мин)
P2	[–78°, –71°]	[–86°, –731°]	[18, 28](м/с)	[19.5, 32](м/с)
Наша	–82°	–86°	35 (м/с)	15.6 (м/с)

выбранное время модели для рассмотренной географической локализации отвечает наиболее частым фактам обнаружения ионосферных возмущений, можно предположить, что реализация условий (где-либо) для двух или более мод, скорее всего, или крайне редка, или отсутствует вовсе.

• •    Три метода (BVPD, BVP и MBSCQ) показали близкие значения как горизонтальной скорости распространения волноводной моды, так и горизонтального затухания. Горизонтальное затухание достаточно мало для сверхдальнего распространения волноводных возмущений. Хорошее совпадение результатов точных методов с результатом формально не применимого для нулевой моды ква-зиклассического описания является достаточно интересным фактом с методологической точки зрения.

• •    Интересно отметить свойство, которое, по-видимому, специфично только для ВГВ-мод с просачиванием. Зависимости на рис. 4 показывают высокую добротность волноводных колебаний при достаточно небольшом уменьшении амплитуды волноводного решения после прохождения барьера непрозрачности [ z 1 , z 2 ]. Параметр Q , определенный в уравнении (3), имеет значение 0.41. В случае обычной акустической волноводной моды такое значение параметра Q привело бы к достаточно сильному горизонтальному затуханию порядка 0.41 ² . Для ВГВ множитель первого члена в уравнении (6) принимает значения порядка 30 (для звука — ~1), обеспечивая высокую добротность мод данного типа. С физической точки зрения этот эффект обеспечивается малостью вертикальной групповой скорости просачивающейся волны.

Важно также отметить, что полученная дисперсионная зависимость нулевой моды очень хорошо воспроизводит характерное соотношение горизонтальных масштабов и периодов наблюдаемых ПИВ. Кроме того, мы имеем хорошее совпадение полученных нами величин полной фазовой скорости в верхней атмосфере с наблюдаемыми фазовыми скоростями ПИВ [Ratovsky et al., 2008; Medvedev et al., 2009]. Эти результаты вполне соответствуют волноводной концепции природы ПИВ. Были проведены более детальные сопоставления свойств волноводных возмущений с наблюдаемыми свойствами ПИВ, описанными в работе [Medvedev et al., 2013]. В этой работе было проведено исследование пространственно-временной структуры на основе анализа данных профилей электронной плотности двух лучей Иркутского радара некогерентного рассеяния и дигизонда.

Прежде всего сравним полученные на основе 12-часового оконного спектрального анализа величины Elevation и Velocity (приведенные на рис. 1,

[Medvedev et al., 2013]) c эквивалентными им по смыслу величинами угловой характеристики Atan ^{vert zc} и скорости с ( z ) соответственно.

k hor ( z c ) ^{p c}

Величины, приведенные в таблице, носят оценочный характер, поскольку они содержат k _vert, условия применения которой на высотах порядка z c не выполняются. Кроме того, наличие на рассматриваемых высотах не учитываемого в теории реального ветра может приводить к существенным смещениям наблюдаемых характеристик относительно теоретических. Для нас достаточно того, что предсказываемые теорией характеристики по своим величинам соответствуют наблюдаемым диапазонам этих характеристик. Представляет также интерес сравнение с наиболее вероятными значениями Elevation, Velocity и Wavelength (≈λ_vert), приведенными на рис. 4–6 из [Medvedev et al., 2013]. Для нас представляют интерес левые части этих рисунков для дневных регистраций в соответствии с используемой нами дневной моделью атмосферы. Отметим, что в дневных регистрациях временной спектр сигналов отвечает ограниченному интервалу периодов приблизительно от ~1 до ~3 ч с двумя локальными максимумами вероятности появления в окрестностях периодов 3 и 1.5 ч (рис. 2, [Medvedev et al., 2013]). Первый максимум — наибольший с малой шириной, второй — более размытый с меньшим значением. Наилучшее соответствие наблюдениям демонстрируют наши величины Elevation и Wavelength. Наиболее вероятное значение Elevation (рис. 4, [Medvedev et al., 2013]), равное –75°, близко нашим значениям (см. таблицу). Наиболее вероятное значение Wavelength 175 км (рис. 6, [Medvedev et al., 2013]) очень близко нашему значению λ_vert=192 км (см. рис. 3). Наиболее вероятное значение Velocity (рис. 5, [Medvedev et al., 2013]), равное 35 м/c, соответствует на нашем

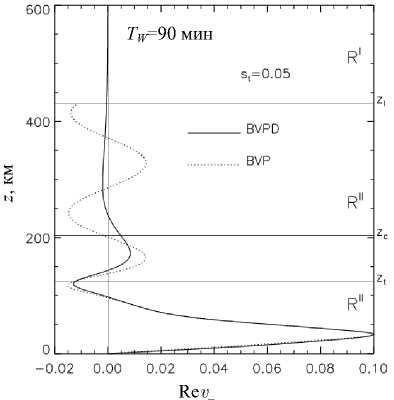
Рис. 5. Пример сравнения ДРНИ с волноводным решением без учета диссипации

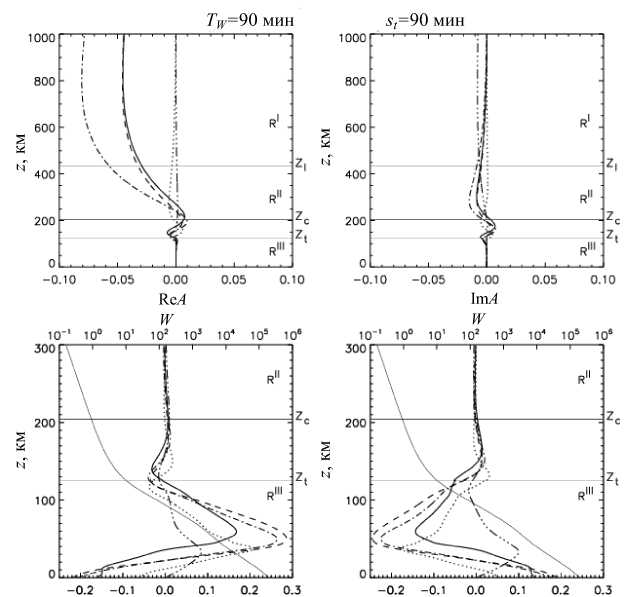
Рис. 6. Полная структура волноводного решения для периода T_W =90 мин. Соответствие линий волновым величинам такое же, как на рис. 6 из [Руденко, Дмитриенко, 2015] (пунктир — Θ; штрих с тремя точками — v ; сплошная — n ; штриховая — f ; штрихпунктир — u ).Тонкая сплошная линия описывает высотное распределение функции W ( z )

графике рис. 3 значению периода T_W =1.4 ч. Это значение T_W соответствует одному из максимумов спектрального распределения (рис. 2, [Medvedev et al., 2013]). Таким образом, мы видим хорошее подтверждение нашего теоретического описания наблюдательными фактами.

3.3.    Высотная структура внутренней гравитационной волноводной моды

После того как волноводные дисперсионные соотношения найдены, для получения высотной структуры волноводного решения нужно рассчитать ДРНИ для двух связанных дисперсионной зависимостью волновых параметров ω и k_x . В схеме решения задачи BVPD эта процедура уже заложена. В схеме BVP мы можем получить зависимость v_z ( z ), используя найденную из BVP-процедуры функцию G ( z , ω, k_x ). Для этого нам достаточно численно проинтегрировать дифференциальное уравнение первого порядка и ‘ = и _ZG G с начальным значением d_z( z^ ) = 1. Мы воспользуемся результатом BVPдля волноводного решения только для его сравнения с решением по нашей основной схеме BVPD. Для сравнения мы используем высотные распределения величины 1/2

и_ ( z ) = Р0—   —. На рис. 5 сравниваются между

• -       lP o (O) J    c z

  собой величины Re решений BVPD и BVP при волновом периоде T_W =90 мин, которому соответствуют собственные значения горизонтального волнового числа k_x =(4.66233·10 ^–3 + i 1.22515·10 ^–5 ) км ^–1 для

  случая BVP и k x =(4.66215·10 ^–3 + i 1.14273·10 ^–5 ) км ^–1 для случая BVP. Мы видим, что оба решения очень близки друг другу в области R ^III , где диссипация мала. Выше них графики, естественно, cущественно различаются. Решение BVP выходит на асимптотику волны в однородной среде, а ДРНИ (BVPD) затухает под воздействием волновой диссипации.

Таким образом, рис. 5 ясно показывает, что волновое описание без учета диссипации справедливо только для ограниченного высотного диапазона, в котором выполняется условие малости параметра s .

Для удобства графического представления ДРНИ мы будем использовать два набора величин. Для отображения верхней части волноводного решения используем 0, n, f, v , u , определенные равенствами (17) из [Руденко, Дмитриенко, 2015]. Для отображения нижней части используем следующие их модификации:

Θ–=WΘ, n–=Wn, f–=Wf, v–=10 Wv u–=Wu.                                    (16)

1/2

Здесь W ( z ) =    —⁰         . Во всех следую-

(р0 (200 км) J щих представлениях волновых решений мы исполь- зуем нормировку max

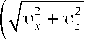
) = 50 м/с.

Обсудим первый пример волноводной структуры на рис. 6. На этом рисунке представлены зависимости от z действительных и мнимых частей всех компонент

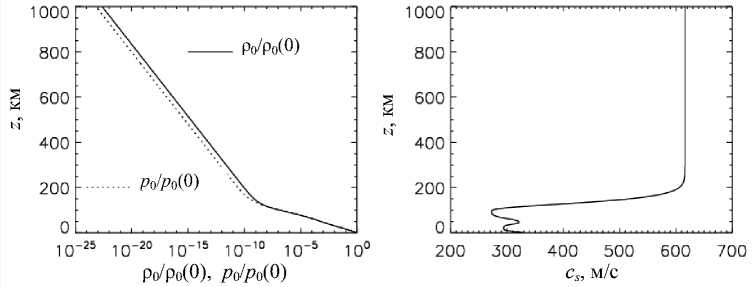
Рис. 7 . Зависимости от высоты невозмущенных величин давления, плотности и скорости звука

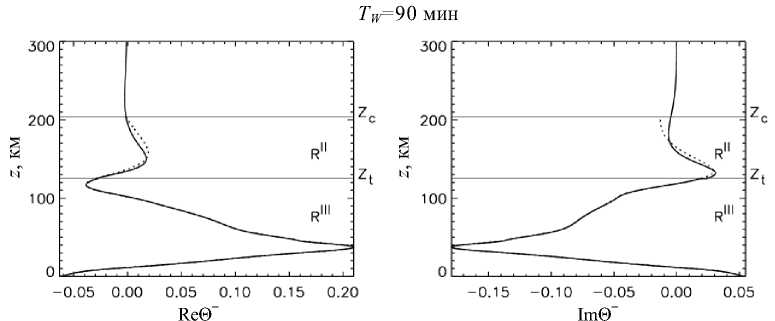
Рис. 8 . Модуль возмущения температуры волноводных решений с диссипацией и без диссипации (сплошная и точечная кривые соответственно)

возмущения ((17) из [Руденко, Дмитриенко, 2015] и (16)). Верхние графики показывают зависимость относительных величин компонент возмущения. Нижние графики описывают детали вертикальной структуры, которые не проявляются на верхних из-за экспоненциального фактора. Мы видим, что относительные величины принимают наибольшие значения в верхней части атмосферы, а абсолютные — в нижней. Достигая некоего максимума, относительные величины начинают уменьшаться вследствие воздействия диссипации. В представленном масштабе все величины выглядят непрерывными на высоте z_s . Показатели разрывности решения для данного случая достаточно малы:

δ [ _Θ ] =δ [ _T ] =δ [ _Θ –] =0.134,

δ [ n ] =δ [ Q ] =δ [n–] =0.095. (17)

Таким образом, мы получили решение, близкое по качеству решениям изотермической модели атмосферы (секция 5, [Руденко, Дмитриенко, 2015]). Отметим, что согласно расчетам показатели разрывности одинаковы по порядку для всех точек дисперсионной кривой.

Отображенные на нижних панелях рис. 6 W ( z ) (тонкая сплошная линия) невозмущенные температура (рис. 1), давление, плотность и скорость звука (рис. 7) дают возможность расчета абсолютных величин возмущений на любой высоте.

Для косвенного теста можно использовать расчет численного параметра, аналогичного параметру показателя суммарного вертикального поглощения η из [Руденко, Дмитриенко, 2015] ((43), [Руденко, Дмитриенко, 2015]) для изотермической модели атмосферы. В изотермическом случае η равен отношению модуля амплитуды T на высоте zc к модулю амплитуды падающей снизу волны без диссипации на этой же высоте. Если, как в нашем случае, доля отраженной волны на высоте zc невелика, то вместо падающей волны без диссипации мы можем использовать полную комбинацию падающей волны с отраженной. Исходя из этого мы выбираем аналогичную η характеристику ηcalc для случая с неоднородной атмосферой. Для вычисления этой величины решаем снизу вверх до высоты zc задачу Коши для системы уравнений (2), (9), (10) из [Руденко, Дмитриенко, 2015], используя в качестве граничных значений значения p и v из ДРНИ на поверхности Земли. Величину ηcalc мы вычисляем как отношение модуля T на высоте zc к модулю T полученного на этой высоте волнового решения без диссипации. Пример такого расчета показан на рис. 8. Этот рисунок еще раз подтверждает, что заметные различия между решениями с диссипацией и без нее начинаются с высоты zs. Видно, что на высоте zc эти решения различаются существенно.

Величину η_calc мы сравниваем с величиной η, рассчитываемой для изотермической модели, в которой температура среды выбирается равной T ₀ неизотермической модели на высоте z_c . Результат сравнения этих величин по всему спектру 0-моды представлен на рис. 9.

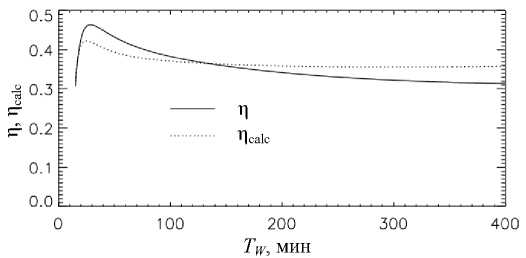
Рис. 9. Сравнение величин η_calc и η

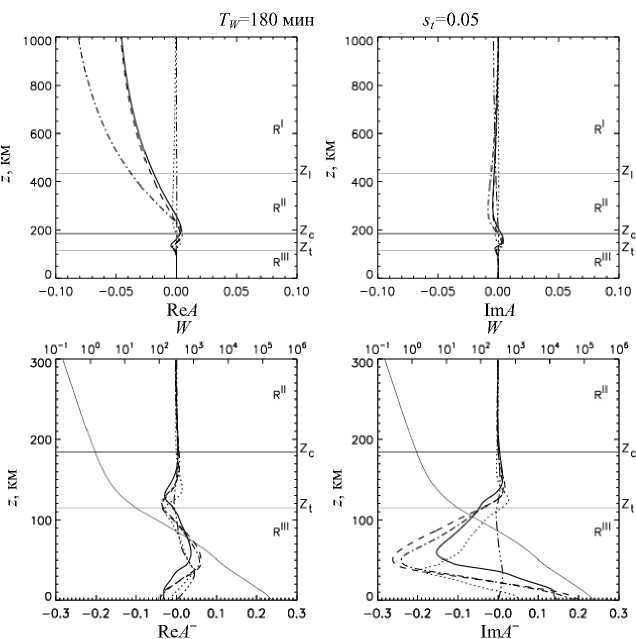
Рис. 10. Полная структура волноводного решения для периода T_W =1 80 мин

Последний рисунок показывает, что порядок величины показателя суммарного вертикального поглощения волнового решения на интервале z =[–∞, z_c ] η=(–∞, z_c )≈η( z_s , z_c ). Близость η_calc изотермическому η является качественным подтверждением правильности ДРНИ. Заметим, что если величины η_calc, η определить через комплексные значения определяющих их величин, то в этом случае комплексные η calc , η совпадают примерно с такой же точностью. Результаты расчетов для комплексных η calc , η мы не приводим.

Для более полного представления волноводной моды мы представляем еще рис. 10–12 для T_W =180 мин и для крайних точек спектрального диапазона T_W =15 мин и T_W =400 мин.

Заметим, что в длинноволновой части спектра (рис. 10, 12) мы не видим прекращения роста некоторых относительных величин в расчетном интервале высот, однако ясно, что они затухают вне его, так как продолжениями численных решений являются затухающие аналитические решения.

ЗАКЛЮЧЕНИЕ

Изучены волноводные моды ВГВ-типа, для которых характерно подбарьерное просачивание в верхнюю атмосферу, обеспечивающее их проникновение на ионосферные высоты. Из-за экспоненциального падения атмосферной плотности убегающее вверх возмущение экспоненциально растет в своих относительных величинах. Это приводит к тому, что наиболее сильное проявление захваченных волн имеет место на больших высотах, вызывая «видимые» перемещения ионосферных возмущений на большие расстояния. Для выбранной нами модели атмосферы мы получили, что при заданной частоте имеет место только одна основная (безузловая) мода. Мы рассчитали дисперсионную кривую для волноводной моды — комплексное горизонтальное число

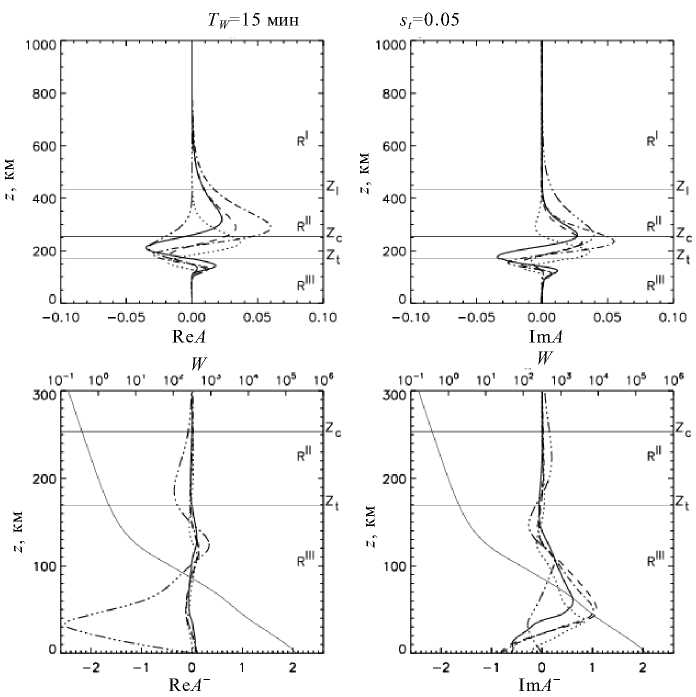
Рис. 11. Полная структура волноводного решения для периода T_W =15 мин

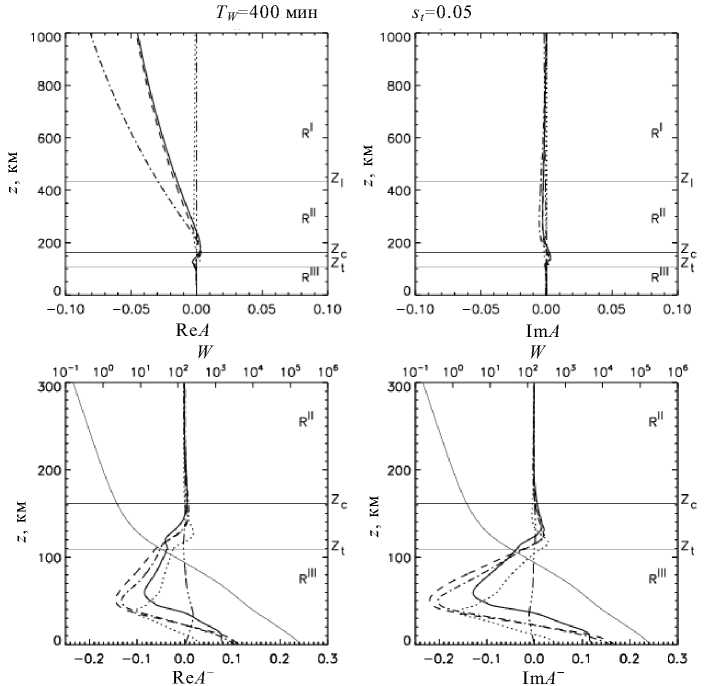
Рис. 12. Полная структура волноводного решения для периода TW=400 мин как функцию действительной частоты. Мы впервые представили во всей полноте на всех высотах вертикальную структуру ВГВ-моды вместе с ее убегающей из волновода частью при полноценном учете диссипации. Такую возможность мы получили благодаря использованию метода построения диссипативного решения над источником, изложенного в [Руденко, Дмитриенко, 2015].

В настоящей работе, кроме диссипативного решения, исследованы также возможности описания без учета диссипации. Показано, что, несмотря на неприменимость в верхней атмосфере, бездиссипа-тивное описание оказывается достаточно полезным в нижней атмосфере. Оно позволяет оценить число мод и получить пристрелочные значения для численного расчета собственных значений; наиболее удобен для этих целей метод ВКБ. Интересно отметить, что ВКБ-описание дает корректные результаты, несмотря на его формальную неприменимость, причем имеет место хорошее совпадение дисперсионных ВКБ-характеристик с точными.

Мы продемонстрировали, что предложенная нами методика не дает каких-либо существенных погрешностей, способных сравниться с погрешностями в наблюдательных данных. В проведенных конкретных расчетах существует не подконтрольная нам погрешность, связанная со статистическим характером модели NRLMSISE. Это самый существенный фактор возможных отличий, получаемых нами в рамках применения этой модели, от наблюдаемых. В силу этого мы должны, вообще говоря, соотносить свои результаты со статистическими наблюдаемыми характеристиками. Поэтому проведенные нами сравнения с экспериментальными данными выглядят достаточно убедительно. Используя полученные дисперсионные соотношения и характеристики волнового распространения просачивающегося возмущения, мы получили очень хорошее соответствие с основными характеристиками наблюдаемых ПИВ: отношение между горизонтальными масштабами и волновыми периодами, способность распространения на многие тысячи километров без существенного затухания; обратное направление вертикальной фазовой скорости; малые значения вертикальной фазовой скорости, специфичный наклон фазового фронта.

Мы благодарны Медведеву А.В. и Ратовскому К.Г. за полезное сотрудничество в процессе написания нашей работы.