Простая имитационная модель экономических кризисов перепроизводства в MATLAB Simulink

Мировая практика показывает, что рыночная экономическая система закономерно развивается, переходя от равновесного состояния к неравновесному и т.д. Но макроэкономическое равновесие на практике – скорее случайность, исключение, подтверждающее правило: рыночная экономика нестабильна [1]. Экономическая история последних двух столетий и начала XXI века дает множество примеров этой нестабильности. За периодами успешного промышленного развития и экономического процветания всегда наступали периоды спадов, сопровождающиеся падением производства и безработицей.

Со времен глобальных экономических кризисов XIX века ученые-экономисты (по крайней мере, большинство из них) пытаются найти причины, вследствие которых экономика выводится из равновесия, и объяснить, почему это происходит через определенные промежутки времени с завидным постоянством.

В литературе [2 - 4] можно найти около десятка различных определений экономического цикла. Но во всех определениях есть и общие положения: экономический (деловой) цикл – это периодические колебания уровня деловой активности, представленного реальным ВВП.

Цикличность [2, c. 442] выступает всеобщей формой движения природы и общества, но в отличие от природных циклов, цикличность в социально – экономическом развитии носит менее выраженный и более противоречивый характер в более короткие по сравнению с историей человечества сроки.

Особенности такого развития экономики связаны с действиями людей со своими целями и изменяющимися средствами их реализации. Все это определяет неоднозначность в трактовке и даже в непризнании самого фактора цикличности [5].

В самом цикле (классический вариант) выделяют четыре фазы: кризис, депрессия, оживление и подъем, причем, главной его фазой является кризис.

Он открывает промышленный цикл и завершает его. Кризис [2, с. 425] – это насильственный взрыв, неожиданный спад в обращении, нарушение равновесия во всей экономике. Он дает толчок развитию экономики, но само развитие идет таким образом, что в конечном итоге подготавливает новый кризис.

Приведенный абзац – концепция детерминистов, которые утверждают, что экономические циклы проявляются с достаточной регулярностью [3].

Представители неоклассической и монетарной школы считают, что циклы – следствие случайных воздействий (импульсов или шоков) на экономическую систему, что и вызывает циклическую модель отклика.

В [3, с. 467] подчеркнуто, что кризис проявляется, прежде всего, в перепроизводстве товаров, сокращении кредитов и повышении ссудного процента. Это ведет к понижению прибылей и падению производства, росту банковских задолженностей, банковским крахам и банкротству предприятий в других сферах экономики.

Однако среди экономистов, которые признают цикличность, нет единства относительно природы этого явления. В [3] выделяются три похода к объяснению цикличности: экзогенный, эндогенный и эклектичный, связывая природу цикла с исключительно внешними, внутренними причинами. Эклектики пытаются найти и объединить рациональные начала первых двух течений. Там же дан, пожалуй, наиболее полный перечень теорий цикличности.

Отметим наиболее адекватную, на наш взгляд, теорию неоклассиков и неокейнсианцев, которые солидарны в том, что одной из основных причин механизма цикличности является процесс приспособления запасов капитала к условиям воспроизводства, которые сами, в свою очередь, меняются под воздействием этого приспособления. Предполагается, что между объемом ежегодно воспроизводимой стоимости - "потоком", с одной стороны, и ее накоплением к данному моменту - "запасом" – с другой, существует "равновесная" пропорция. Пока она не нарушена, циклических колебаний быть не может. И наоборот, коль скоро колебания есть, то это означает, что фактическая пропорция поток/запас отклоняется то в одну, то в другую сторону от равновесной величины. При этом происходят колебания как производства, так и капитала. Например, в [4, с. 255] изображены темпы прироста ВВП в четырех наиболее успешно развивающихся во второй половине XX века странах, которые имеют явно выраженную циклическую зависимость от времени.

Уместно отметить, что некоторые экономисты (австрийская экономическая школа) считают, что экономический цикл не является частью рыночной экономики, а порождается в стране центральным банком и усугубляется всевозможными разновидностями государственного вмешательства [5].

Математическая модель экономических циклов

Кратко опишем, опираясь на [4], модель П. Сэмуэльсона – Дж. Хикса, которая включает в себя только рынок благ, поэтому уровень цен и ставка процента предполагаются неизменными; объем предложений благ совершенно эластичен.

Объем потребления домашних хозяйств C в текущем периоде t зависит от величины их дохода в предшествующем периоде t - 1

Ct = Ca,t + Cy * yt—1, где Ca - автономное потребление; C - предельная склонность к потреблению          по доходу; y - величина реального национального дохода.

Предприниматели (поставщики) осуществляют автономные инвестиции I , объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции I , зависящие от прироста совокупного спроса в предшествующем периоде, равны

It = Ia ,t + n'( yt—i — yt—2>- где n = ^K / Ау  - коэффициент, показывающий, сколько единиц дополнительного капитала требуется для производства дополнительной единицы продукции (коэффициент приростной капиталоемкости – акселератор). При данном n для увеличения производства от у0 до у^ необходимы индуцированные инвестиции в размере

Iin = П *( У1 ^- У ₀).

На рынке благ установится динамическое равновесие, если yt = C + C * у ,+1 + n*( у - у ) = (C + n )* у - n* у + A ,            (1)

yt a , t ^{у  y}t - 1    a , t    '   ^ t - 1   ^у1 - 2’  ^v у ⁿ -^t - 1    '   ^у1 - 2    t^{,                (} )

где At = Cat + 1^ + Gt ; Gt - реальный объем государственных расходов.

Уравнение (1) является неоднородным конечно – разностным уравнением второго порядка, характеризующим динамику национального дохода y во времени.

При фиксированной величине автономных расходов ( A = A = const ) в экономике достигается динамическое равновесие, когда объем национального дохода стабилизируется на определенном уровне y , т.е. у _— = у^ ₁ = у ^_2 = ... = у _— - _n = у , где n - число периодов с неизменной величиной автономных расходов A .

Из (1) следует, что у = A /(1 - Cy). Проанализируем, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса Ca. Запишем однородное уравнение, приняв в (1) A = 0, и обозначив Ayt = yt - y:

^A yt = ⁽ Cy + n )* ^A yt - 1 ^- n * ^A yt _{- 2}.                        (2)

Соотношение (2) являет собой однородное конечно – разностное уравнение второй степени с постоянными коэффициентами. Т.к. y_t = y + A y_t , то направление изменения y определяется направлением изменения приращения A y_t .

Из теории дифференциальных и конечно – разностных уравнений [6] следует, что характер изменения Ayt зависит от дискриминанта характеристического уравнения, получаемого из (2). Поскольку (2) можно преобразовать к виду y"t-(Cy + n )* y‘-n* y = 0,                  (3)

то характеристическое алгебраическое уравнение будет:

Я ² - ( Cy + n )* X-n = 0.                     (4)

Дискриминант уравнения (4) равен D = ( Cy + n )² - 4* n . Тогда динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора ( Cy +n ) и акселератора n . Если D >  0, то изменение y происходит монотонно; при D <  0 оно будет колебательным.

Устремляется ли значение y к некоторой конечной величине или y ^да , зависит от последнего слагаемого n в (4). Если n <  1, то равновесие установится на определенном уровне. При n >  1 нарушенное один раз равновесие больше не восстанавливается. Когда n = 1, значение yt будет колебаться с конечной амплитудой.

Как замечено в [4], в описанной модели не были учтены следующие обстоятельства:

• 1.    Произведенный национальный доход не может существенно превысить национальный доход полной занятости; этим будет ограничиваться амплитуда колебаний y сверху.

• 2.    Объем отрицательных индуцированных инвестиций не может превысить сумму амортизации; это ограничивает амплитуду y снизу.

Имитационная лабораторная модель в MATLAB Simulink

Последние 75 лет кризисы перепроизводства, как правило, начинались в автомобильной промышленности и через 5 – 10 лет после окончания глобальных войн. Поэтому предположим, что в нашей модели промышленность выпускает автомобили [7].

Структурная схема имитационной модели циклов и кризисов в Simulink представлена на рис. 1.

Моделирование потребности в парке автомобилей ( y в математической модели) на схеме задано блоками константы и интегратора непрерывного времени, расположенными слева вверху. На выходе интегратора формируется линейный во времени поток потребности населения в парке автомобилей с именем NeedPark (необходимый парк). Ниже блоков потребности расположены четыре блока, отражающие движение парка автомобилей: поступление автомобилей в эксплуатацию от производителей -переменная Prdct (продукт), накопление их в парке (на рынке) интегратором 1 с выходной переменной Inpark (в парке). Блоки Srok slughbi и Vibitie, представляющие собой стандартные блоки временной задержки сигналов и интегратор непрерывного времени, соответственно, задают переменную OutPark (поток выбытия автомобилей по ветхости, износу в результате эксплуатации или моральному старению).

Нижний блок (круглый) сумматора вычитает из поступившего на его левый вход в парк оборудования (InPark) выбывшее (по стоимости), создавая переменную RealPark (реальное количество по стоимости автомобилей, находящихся в эксплуатации). Верхний блок сумматора вычитает из необходимого наличный парк, создавая переменную текущего спроса CurDmd. Блоком Saturatuon (ограничитель) она «обрезается» снизу, реализуя традиционную для экономических задач не отрицательность переменных: CurDmd ≥ 0. Блок производства (поставщики товара) с его системой управления задаем в виде упрощенной модели.

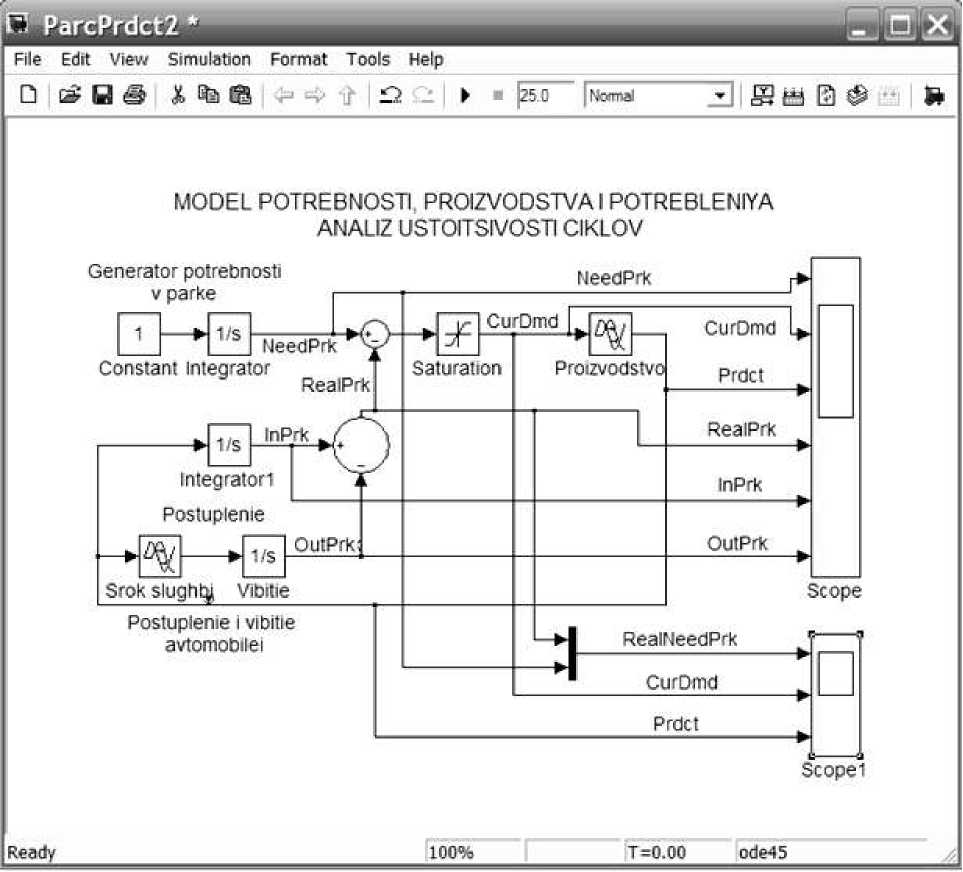
Рис.1. Simulink модель анализа циклов и кризисов

Производство выполняет заказ полностью, но с фиксированным сроком выполнения, задаваемым блоком задержки (лаг исполнения заказа).

Для анализа результатов моделирования и управления экспериментами в модель добавляются блоки Scope (виртуальный осциллограф) отображения информации и линии связи между блоками, по которым идут финансовые потоки.

В окнах блоков Scope наблюдаются графики изменения показателей экономической динамики во времени, рис.2.

Для рис. 2 общее время моделирования выбрано равным 25 лет. Параметры блоков Scope и Scope1 установлены так, чтобы обеспечить удобное восприятие и последующий анализ результатов моделирования. Приведем установленные параметры основных блоков модели.

Блок интегратора в Generator potrebnosti v parke имеет начальное условие, равное 100 (допустим, миллиардов $). Решатель модели использует метод численного интегрирования ode-45 – метод Дормана – Принса с переменным шагом. Блок Saturation имеет параметры: нижнее ограничение 0, верхнее – 2000 млрд. $. Лаг производства установлен равным 3 года.

Интегратор1 блоков Postuplenie i vibitie avtomobilei а также интегратор блока vibitie имеют одинаковые нулевые начальные условия (отсутствие дефицита). Параметр задержки блока Srok slughbi равен 3 года.

На экранах виртуальных осциллографов наблюдаются явно выраженные колебания исследуемых экономических переменных, что свидетельствует о цикличности и кризисах в модели производства – потребления автомобилей.

Разработанная модель позволяет исследовать зависимость устойчивости экономической системы при различных лагах производства. Экспериментатор может изменять параметр задержки (например, в годах) в блоке Proizvodstvo (см. рис.1) стандартного блока временной задержки сигнала. С увеличением задержки, т.е. отставания реакции производства на спрос (неэластичность), возрастает амплитуда и период колебаний системы, т.е. снижается ее устойчивость, возрастает возможность возникновения кризисов. Экспериментатор также может изменять параметр задержки в блоке Srok slughbi. С увеличением задержки возрастает амплитуда и период колебаний экономической системы, появляется возможность наступления кризиса перепроизводства, т.к. потребитель «неохотно» расстается со своим старым автомобилем и не спешит посетить автосалон, чтобы подобрать себе подходящий по большинству предпочтительных параметров новый автомобиль. Это характерно для отраслей производства, производящих товары долгосрочного пользования или длительного хранения. Для товаров разового потребления при нулевых задержках производства колебания спроса – предложения не возникают, т.к. предложение всегда равно спросу. Система устойчива. Но такая система должна иметь другую модель.

У автора имеются ряд наработок использования программы MATLAB с блоком Simulink, в которых разработаны, отлажены имитационные модели динамики экономических процессов. Полученные при их использовании результаты позволяют наглядно осмыслить динамику явлений во времени. Проведенное моделирование показывает адекватность созданных структур, не противоречащих здравому смыслу, экономической теории и практике [9,10].

Естественно, имитационное моделирование не является панацеей при преодолении кризисных явлений, но во многом способствует пониманию их возникновения и даже может в какой-то мере может помочь преодолеть сбои. Кроме того, экспериментатор может исследовать влияние начального дефицита на устойчивость производства в модели. Под начальным дефицитом понимается в нашем случае разница между

а)

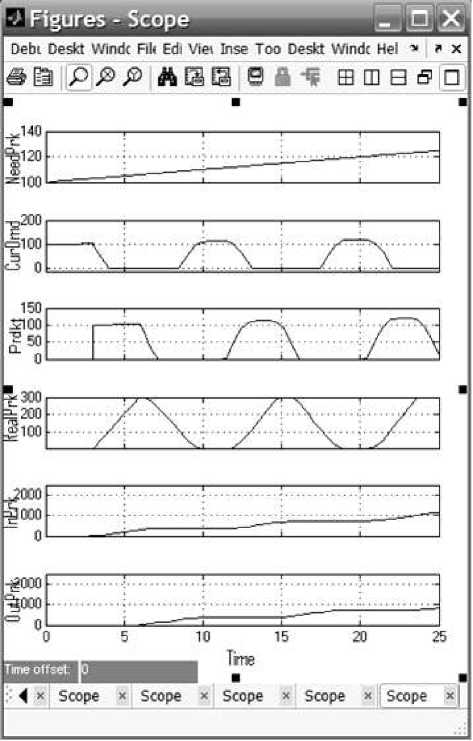
Рис.2. Графики экономической динамики производства, спроса, потребления Scope - а); производства, спроса и потребления Scope1 - б)

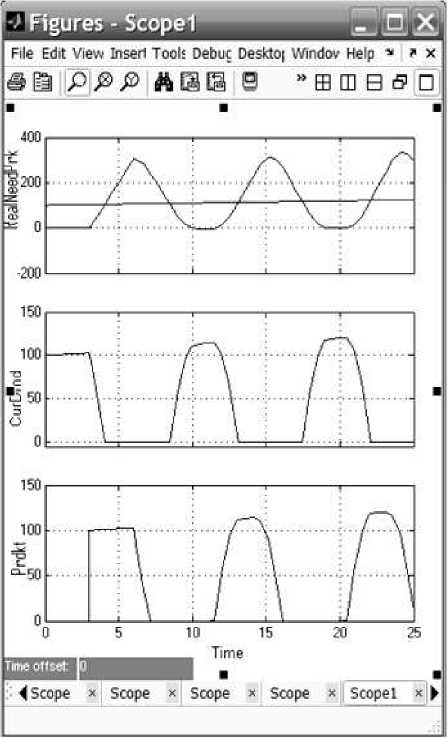
б)

необходимым и реальным парком автомобилей на момент начала моделирования. При этом он изменяет величину начальных условий в интеграторе (блок Postuplenie), варьируя величиной начального реального парка автомобилей. С увеличением дефицита возрастает амплитуда колебаний спроса – предложения, снижается устойчивость системы, возрастает возможность начала кризиса.

Приведенные рассуждения и выводы теоретически обосновываются следующим положением. В теории автоматического управления (ТАУ) утверждается, что в системах с обратной связью (ОС) и запаздыванием из – за наличия в системе колебательного звена второго порядка при подаче на вход системы испытательного «ступенчатого» сигнала внутри системы и на ее выходе возможны колебания и неустойчивость, которая усиливается астатизмом, т.е. накоплениями [6]. В нашей модели (рис.1) существуют, по крайней мере, две «отрицательные» ОС, т.е. модель реализует колебательное звено второго порядка, реакция которого на входной «сигнал» описана в теоретическом исследовании характеристического уравнения второго порядка с постоянными коэффициентами при анализе математической модели экономических циклов Сэмуэльсона – Хикса.

Проведем исследование устойчивости системы в зависимости от:

• а)    производственного лага в блоке Proizvodstvo модели рис.1. В этом случае установим параметр Time Delay (время задержки) равный 3 года;

• б)    срока службы автомобилей. Установим в блоке Srok slughbi время задержки равным 2 года;

• в)    начального дефицита. Установим параметр Initial condition (начальные условия) в интеграторе блока Postuplenie равным 0 (нет дефицита).

Результаты моделирования изображены на рис. 2. Из осциллограмм блока Scope (рис.2 а)) видно, что колебания переменной CurDmd (текущий спрос) находятся «в противофазе» относительно переменной Prdkt (продукт, производство), что способствует кризису из-за влияния лага производства. В идеальном равновесии спрос должен определять предложение (колебания этих переменных должны иметь одинаковую фазу (быть синфазными)). Заметим также, что общее время моделирования равно ~ 25 годам. Амплитуды колебаний переменных имеют слабую тенденцию к росту, который задается глобальной переменной NeedPark.

Оставим неизменным значение лага производства, величину дефицита, но изменим величину срока службы автомобилей, задав ее равной 5 годам. Результаты моделирования при таких параметрах приведены на рис. 3.

Из рис. 3 видно, что по сравнению с рис. 2 период колебаний всех переменных увеличился до ~ 10 лет, т.е. вырос в два раза; амплитуда переменных RealPark и RealNeedPark выросла до ~ 400 единиц, что свидетельствует об усилении кризиса.

Результаты моделирования в зависимости от дефицита в работе не приведены вследствие ограниченного объема.

Автор проделал эксперименты по исследованию влияния дефицита на параметры цикличности экономических процессов. При значении начального условия Integrator1 блока Postuplenie, равного ~ 30 млрд. $, все циклические колебания имеют амплитуды, ~ на 30% меньшие, чем для параметров модели, реализованных на рис.2, примерно с теми же периодичностью и несинфазностью, т.е. имеет место положительное влияние явного уменьшения дефицита. При начальном условии, равном 100 млрд. $ колебания практически затухают. Циклов и кризисов нет, т.е. запас автомобилей в таком объеме "гарантирует" стабильность, по крайней мере, на 25 лет.

Результаты моделирования показаны на рис. 4.

Покажем, как можно изменить параметры блока Scope, чтобы виртуальные осциллограммы изображались не на черном фоне, как это запрограммировано изначально, а имели стандартный вид черно – белых графиков, что гораздо удобнее для восприятия. Для этого после отладки из запуска модели рис.1 в командном окне программы MATLAB вводим команды [8]:

set(0,'ShowHiddenHandles','On')

set(gcf,'menubar','figure') и запускаем их на выполнение. В результате стандартное окно блока Scope приобретает вид рис.2, где появляется командная строка с меню Edit, позволяющее пользователю изменить по своему усмотрению параметры фигуры, осей и т.п.

Таким образом, созданная модель позволяет в рамках упомянутых ограничений исследовать и прогнозировать динамику циклов и кризисов в зависимости от основных экономических параметров блоков имитационной модели.

С более полной тематически похожей имитационной моделью автора можно познакомиться в работе [11].

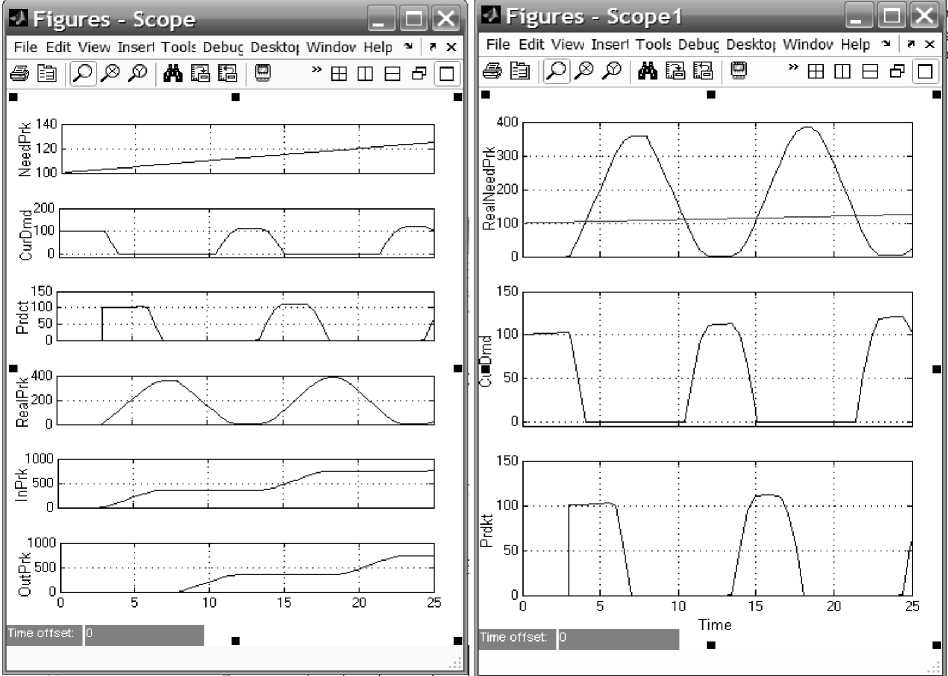
Рис.3. Графики экономической динамики при сроке службы автомобилей 5 лет

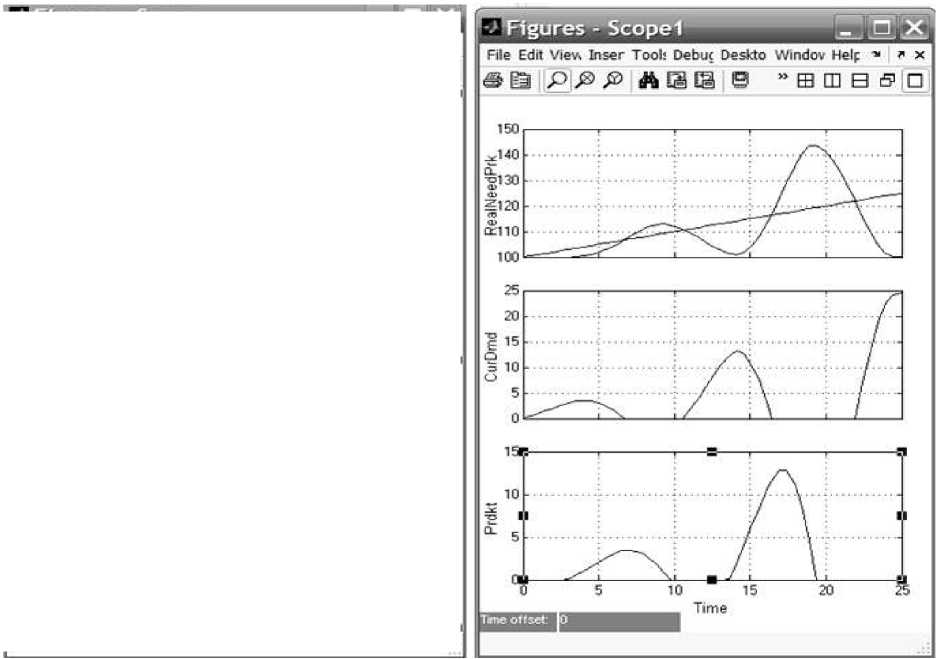
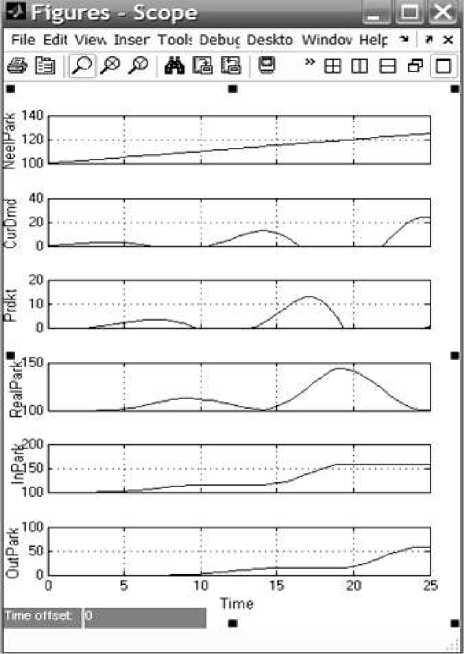
Рис. 4. Динамика экономических процессов при начальном значении блока Postuplenie, равном 30 млрд. $