Простая конечно-элементная модель удлинения образца тканого полотна

Механические свойства текстильных тканых полотен зависят от двух групп факторов. Первая группа ‒ это механические характеристики и свойства нитей основы и утка, из которых сформировано полотно. Вторая группа факторов определяет особенности переплетения нитей, которые зависят от геометрии раппорта и фазы строения. Как известно, фаза строения определяется по величине изгиба нитей основы и утка в областях их перекрытия и их окрестностях (проф. Н. Г. Новиков, [1, 2, 3]).

Текстильные полотна, выработанные из пряжи или/и нитей, являются уникальными искусственными материалами, созданными человеком и не имеющими аналогов в природе. Изделия из полотен представляют собой плоские или искривленные поверхности, площадь которых обычно составляет десятки квадратных дециметров или метров. Размеры раппорта переплетения двух систем нитей ‒ основы и утка ‒ ничтожно малы по сравнению с этими площадями. Однако при этом все основные свойства полотен определяются именно особенностями переплетения [7, 8, 9].

Можно построить аналогию с полимерными материалами, свойства которых зависят от свойств, расположения и взаимодействия огромных молекул полимера, которые, однако, несмотря на огромные для микромира размеры, несоизмеримо меньше размеров изделий из этих полимерных материалов. Но есть и важнейшие отличия между текстильными полотнами и, например, полимерными пленками [6, 8, 10].

Взаимодействие молекул полимера подчиняется законам квантовой механики, статистической физики и термодинамики. Взаимодействие нитей и волокнистых продуктов (например, пряжи) подчиняется законам классической механики. При этом специфика структуры и взаимодействия этих механических конструкций в ткани требует адаптации общих законов классической механики к этим объектам, чтобы получить возможность решать необходимые прикладные задачи. Огромное количество точек взаимодействия, распределённых по поверхности полотна, и безусловное наличие статистического разброса значений переменных и параметров, хотя бы в малых пределах, между точками взаимодействия, означает, что наиболее естественным было бы включить в список используемых методов классическую статистическую механику [9, 10].

Взаимодействие элементов волокон и нитей в ткани происходит в результате их точечных или поверхностных контактов. Оно приводит либо к деформациям самих элементов, либо к их смещениям. Эти изменения можно разделить на консервативные и диссипативные. Первые не приводят к потерям механической энергии, вторые необратимым образом переводят механическую энергию деформации и перемещения элементов волокон и нитей в тепловую энергию. Именно благодаря диссипативным свойствам тканый материал, принимая на себя внешние механические воздействия, «гасит» их энергию, распределяя ее по своей поверхности и переводя ее в тепло. Для прогнозирования механических свойств полотна на основе свойств нитей и переплетений разработано большое число различных геометрических, математических и компьютерных моделей. Некоторые из них рассмотрены, например, в [3, 4, 5, 6, 9, 10]. Однако проблема моделирования продолжает оставаться актуальной и привлекать внимание многих исследователей. Здесь приводится двумерная модель тканого полотна в пределах линейно-упругой составляющей деформации. Она основана на методе конечных элементов и позволяет учесть структурные особенности ткани.

Рассмотрим прямоугольный образец тканого полотна. Его проекция на плоскость, параллельную плоскости образца, состоит из участков трех типов. Первый тип ‒ это «поры» ‒ участки полотна, не заполненные нитями. После формирования ткани и ее последующей обработки нити частично расплющиваются в плоскости полотна и могут полностью или частично закрыть эти участки. В некоторых видах полотен, например, марли или сети, поры создают специально. Важно, чтобы размеры этих пор не слишком сильно отличались от проектных значений.

Второй тип участков ‒ это перекрытия основы и утка. На эти участки попадают проекции, как минимум, одной нити основы и одной ‒ утка. В многослойных тканях на эти участки могут проектироваться и больше двух нитей. Перекрытия и тесный контакт между нитями, усиленный трением и сцеплением между нитями и волокнами внутри нитей на этих участках, являются главными факторами, от которых зависят механические свойства и целостность данного участка полотна.

Третий тип участков ‒ это проекции участков нитей одной из систем ‒ основы или утка ‒ между участками перекрытий. В однослойных полотнах эти участки образуются проекциями одной из нитей. В многослойных тканях на эти участки могут попадать участники нескольких нитей, которые, однако, в отличие от участков второго типа, непосредственно не контактируют, лишь их проекции попадают на один и тот же участок плоскости. На таких участках механические свойства полотен определяются свойствами только этих нитей.

Простейшим видом механического воздействия на прямоугольный образец полотна является его удлинение вдоль одной из его сторон (и одной из систем нитей ‒ основы или утка) с сохранением плоской формы образца. Стандартные размеры образца для такого воздействия в лабораторных условиях равны 0,20 м вдоль удлинения и 0,10 м в поперечном направлении. Для определенности будем считать, что удлинение образца происходит вдоль нитей основы. При плотности ткани по утку 4000 нитей/м получим, что на нагружаемой части образца находится порядка 800 нитей утка.

Модель удлинения образца основана на замене ткани сплошной деформируемой средой в двумерном пространстве. При быстром монотонном удлинении образца эффектами релаксации и пластической составляющей деформации можно пренебречь. В линейной упругой модели материал описывается двумя параметрами: модулем упругости E и коэффициентом Пуассона ν. Чтобы учесть особенности периодической структуры ткани, обусловленные раппортом переплетения и параллельными нитями основы и утка, значения E и µ будем описывать периодическими функциями координат. В качестве простейшего примера таких функций выберем следующие зависимости, приближенно отвечающие однослойной ткани полотняного переплетения:

E(x,y) = 2e9 ( 1 + 0.6sin ( 2 n x/0.0005 ) cos ( 2 n y /0.0005 )) , Pa; v (x,y) = 0.2 (( 1 + 0.6 sin ( 2 n x / 0.0005 ) cos ( 2 n y / 0.0005 ))).

Значения E и ν меняются синхронно по обеим осям с периодом T = 0,0005 м. При удлинении образца на 10 % (0.02 м) в образце возникают механические напряжения и пропорциональные им деформации в плоскости образца. Используем для моделирования этих напряжений и деформаций метод конечных элементов, построив в пределах геометрической модели образца сетку конечных элементов прямоугольной формы. Число элементов 5000, число степеней свободы 40602, моделирование выполнено в системе Comsol 4.

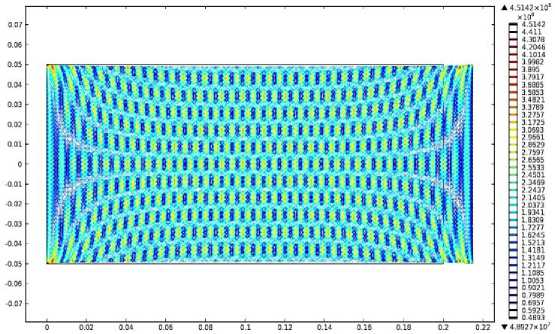
В качестве интегрального показателя напряженного состояния деформируемой сплошной среды, использованной в качестве модели образца, принято использовать так называемое эквивалентное «напряжение по фон Мизесу». Распределение этого напряжения по плоскости удлиненного образца показано цветной контурной диаграммой на рисунке 1. Видно, что наиболее напряженными и деформированными являются участки по углам образца.

(«1 a V? и i и ш«ш m i ш и имМЛIi у b 1 Ш M i в И i Ш И Ш Ш i 6 Ш ||ШШ1!1!ШИИШИ<НШИИ

АPV/й Ш । н m ш ш ш I ш ДУ tJ к

Third principal strain (1)                  First principal strain (1)                  Von Mises stress (N/m2)

Рисунок 1 ‒ Контуры равных механических напряжений по фон Мизесу

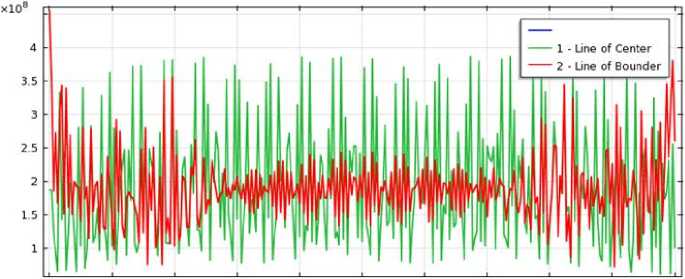
Line Graph: von Mises stress (N/m2)

O 0.02      004      0.06      0.08       0.1       0.12      0.14      0.16      018      0.2

Arc length

Line Graph: First principal strain (1)

0.3 0 28 0 26 0 24 022

0.2 0.18 016 0 14 0 12

0.1

0 08 0 06 0.04 002

----1 - Une of Center ----2 • Une of Bounder

l^ll^^

0       002      004     006     008      0.1      0.12      014      0.16      018      0.2

Arc length

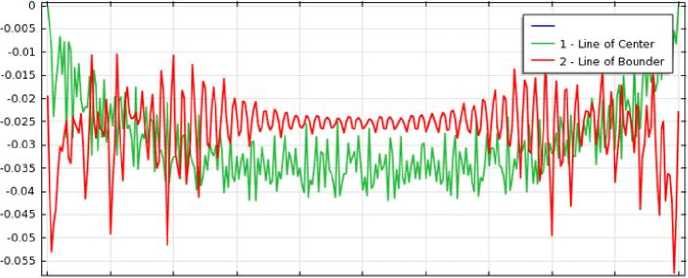
Line Graph: Third principal strain (1)

0       002      0.04      0.06      008       0.1       0.12      0.14      0.16      018      0.2

Arc length

Рисунок 2 ‒ Напряжения и относительные продольные и поперечные деформации по длине образца

в его середине и по краю