Простая расчетная модель определения температурных напряжений в цилиндрической оболочке от градиента температуры по толщине ее стенки

Температурные воздействия относятся к дилатационным воздействиям, они являются распределенными во всем объеме и в случае препятствия тепловой деформации возникающие температурные напряжения могут быть весьма существенными. Для дымовых труб с газоотводящим каналом, совмещенным с основными несущими конструкциями, температурные напряжения, вызванные перепадом температур по толщине стенки, могут быть больше, чем от всех других нагрузок и воздействий. Простые расчетные модели особенно востребованы для выбора конструктивного решения при вариантном проектировании.

Исходными данными для определения температурных напряжений являются вычисления температурных полей. Традиционно задача определения температурных напряжений решается через определение реактивных усилий, препятствующих температурной деформации единичных элементов конструкции [1, 2], при этом величина усилий зависит от изгибной жесткости, то есть толщины стенки. Отметим,что толщина стенки входит и в расчет ее фиктивной кривизны от перепада температур.

В отличие от пластинки, которая коробится от разницы температур на поверхностях, при осесимметричном изменении температур на поверхностях цилиндрической оболочки, вследствие ее замкнутости, она изменяет свои линейные размеры, но не меняет формы. Это позволяет упростить расчетную модель определения температурных напряжений.

Рассмотрим полоску, вырезанную из цилиндрической или слабо конической оболочки, например ствола дымовой трубы (см. рисунок). При относительно тонкостенной оболочке нет существенной разницы направления вырезки (кольцевое или продольное). От внутреннего нагрева возникает разность температур на внутренней и наружной поверхностях и полоска стремится изогнуться, но этому мешают соседние участки оболочки. То есть реактивные силы от них выгибают полоску в об-

Серия «Строительство и архитектура», выпуск 14

Научно-методический раздел

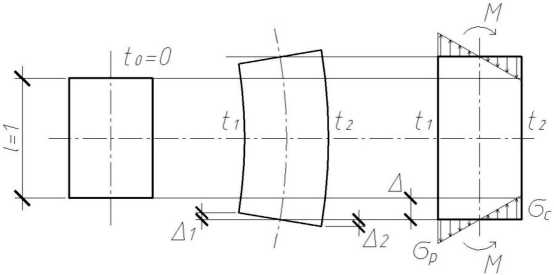
Схема к определению температурных напряжений

ратном направлении. Для сохранения формы полоски этот обратный выгиб должен быть равен температурному искривлению свободной полоски. На основе этих вычислений и определяют температурные напряжения [1, 2]. Обратим внимание на то, что при сохранении формы оболочки, деформации на ее наружной и внутренней поверхностях уравниваются между собой и равны температурной деформации оболочки в целом (или ее расчетного элемента). Отсюда можно определить долю силовой деформации как разницу температурных деформаций поверхностей и оболочки в целом. По величине этой силовой деформации определяются температурные напряжения, при этом исключаются промежуточные операции определения реактивного момента, кривизны, вызванной этим моментом, и фиктивной кривизны от перепада температуры.

Для рассматриваемого элемента единичной длины (см. рисунок) составляющие его относительной деформации численно будут равны составляющим его абсолютной деформации.

Исходя из схемы, показанной на рисунке, при коэффициенте линейного температурного расширения (КЛТР) а и повышении температуры от исходной равномерной 1 ₀ (для простоты примем равной 0) на 1 ₂(внутренняя нагретая поверхность) и на 1 1 (наружная поверхность):

Д= 0,5 “^(tl+t2) ;

Д1= Д — ~~ = 0,25a(t2 — ti);

д2=^2-д= Q,25a(t2 -11).

При постоянном значении модуля упругости материала Е (что может быть без большой погрешности принято для труб кирпичных, железобетонных и металлических) величина температурных напряжений составляет:

ар = д1Е = 0,25Ea(t2 - tj;

^с = д2е = 0,25Ea(t2 - t1).

Как видим, величина температурных напряжений непосредственно зависит только от модуля упругости материала Е, его КЛТР а и от перепада температур внутренней и наружной поверхности оболочки (t2 — t1). Толщина стенки ствола оказывает влияние на температурные напряжения через изменение с толщиной термического сопротивления стенки, которое влияет на разность температур внутренней и наружной поверхностей оболочки.

При линейной зависимости модуля упругости от температуры (при 1 1 - Е 1 , при 1 ₂ - Е ₂)

| ° />| = 1° J = 0,25 Е1 " Е2 «(12 - 11 ).

Реактивный момент М от теплового воздействия (на единицу ширины) (например, для подбора сечения арматуры в железобетонной трубе и стяжных колец в кирпичной дымовой трубе) может быть определен как произведение вычисленных температурных напряжений ° на момент сопротивления W стенки толщиной h :

M = ° W = ° h ²/б .

Сравнивались результаты расчета температурных напряжений по предлагаемой модели и через определение фиктивной кривизны от перепада температуры и реактивного момента для ликвидации этой кривизны по [2] для стенки железобетонной дымовой трубы и по [1] для стенки стеклопластикового газохода. В обоих случаях расчет по предлагаемой модели и по существующей более сложной методике дал одинаковый результат.

Таким образом, с применением предлагаемой расчетной модели задача определения температурных напряжений и реактивных моментов в замкнутой цилиндрической и близкой к ней по форме оболочке может быть упрощена.