Простейшие формулы естественного отбора

Для гаплоидной панмиктической популяции найдены следующие     зависимости:     времени отбора фенотипически полезной аллели от численности популяции и относительной приспособленности аллели; частоты отбираемой аллели от времени; скорости отбора от времени; скорости отбора от частоты аллели. Показано, что время, за которое частота отбираемой аллели изменяется от а до b, не зависит от численности популяции.

Можно сказать, что частота отбираемой (фенотипически полезной) аллели на всем возможном диапазоне (от нуля до единицы) закономерно увеличивается. Что значит закономерно? Это значит, что время, за которое частота отбираемой аллели изменится от а до b ( а меньше b ), является не случайной величиной, а функцией каких-то переменных. Т.е., если в какой-то популяции частота какой-то фенотипически полезной аллели равна а ; и если известны значения всех переменных, функцией которых является время отбора; и если известно, какие математические операции надо произвести с этими значениями — то можно с хорошей точностью рассчитать время, через которое частота рассматриваемой аллели примет значение b .

Конечно, Дарвин сформулировал другими словами, но смысл его открытия именно такой: существуют аллели, время изменения частоты которых - функция каких-то переменных . Для гаплоидных панмиктических популяций можно записать эту функцию в общем виде.

Пусть в какой-то гаплоидной панмиктической популяции со стабильной численностью (численность популяции равна A особей) идет замещение одной аллели другой (фенотипически более полезной) аллелью. В начальный момент времени число замещаемых аллелей практически равно A , в конечный момент времени число замещающих (отбираемых) аллелей практически равно A. Надо найти время, за которое частота замещающей аллели изменится от нуля до единицы. (Ясно, что за это же время частота замещаемой аллели изменится от единицы до нуля.) Пусть в какой-то момент времени число замещаемых аллелей равно a, число замещающих аллелей равно b. Пусть через единицу времени число замещаемых аллелей становится равно c, число замещающих аллелей становится равно d. Тогда потомство одной особи с замещаемой аллелью в среднем за единицу времени равно c/a. Соответственно, потомство одной особи с замещающей аллелью в среднем за единицу времени равно d/b. Надо сказать, что в популяционной генетике принято пользоваться относительной приспособленностью замещаемой аллели. Для того, чтобы найти относительную приспособленность замещаемой аллели в рассматриваемом случае, надо c/a разделить на d/b. Относительная приспособленность замещаемой аллели в рассматриваемом случае будет показывать, какую часть составляет полноценное потомство одной особи с замещаемой аллелью от полноценного потомства одной особи с замещающей аллелью в среднем за единицу времени. Но ведь можно сделать и наоборот: найти относительную приспособленность замещающей аллели, т.е. разделить d/b на c/a. Относительная приспособленность замещающей аллели в рассматриваемом случае будет показывать во сколько раз полноценное потомство одной особи с замещающей аллелью больше полноценного потомства одной особи с замещаемой аллелью в среднем за единицу времени. Далее «относительная приспособленность» - w – это относительная приспособленность замещающей (отбираемой) аллели dc db

Итак, w = V ■ —, откуда w = •_, где b/a — это отношение ba ca числа замещающих аллелей к числу замещаемых аллелей, d/c – также отношение числа замещающих аллелей к числу замещаемых аллелей, но через единицу времени. Значит, относительная приспособленность замещающей аллели показывает, во сколько раз увеличится отношение числа замещающих аллелей к числу замещаемых аллелей за единицу времени.

Пусть в начальный момент времени отношение числа замещающих аллелей к числу замещаемых аллелей было равно 1/А (т.е. была одна особь с замещающей аллелью и А-1 особей с замещаемой аллелью, а т.к. A большое число, то 6

А ~А-1).   Тогда в момент времени t отношение числа wt

A ^.

замещающих аллелей к числу замещаемых аллелей равно

В конечный момент времени T , когда останется одна особь с замещаемой аллелью, отношение числа замещающих аллелей к

T wT числу замещаемых аллелей равно A. Т.е. A — —^, откуда

2ln A ln w ^.

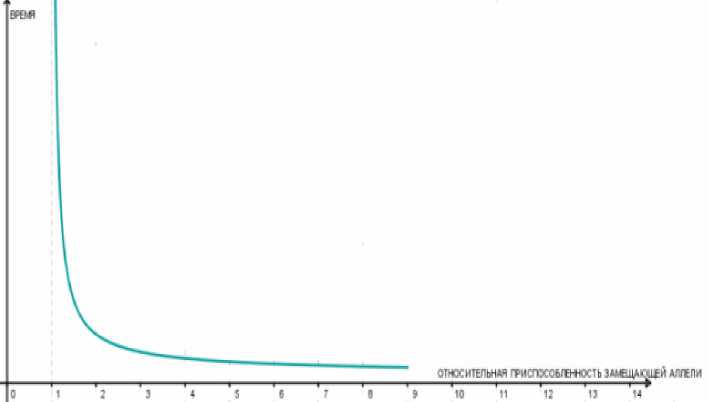
Рис. 1 – зависимость времени полного замещения одной аллели другой аллелью от относительной приспособленности замещающей аллели.

Из графика на одной аллели другой

рис 1 видно, что время полного замещения аллелью (время отбора) очень чувствительно к малейшим изменениям относительной приспособленности замещающей аллели, если эти изменения происходят рядом с единицей. Кроме того, очевидно, что расчетное время отбора может быть как угодно велико.

Можно также найти зависимость частоты замещающей аллели от времени. В момент времени t отношение числа замещающих wt аллелей к числу замещаемых аллелей равно A . Пусть в этот же момент времени частота замещающей аллели равна p. Тогда

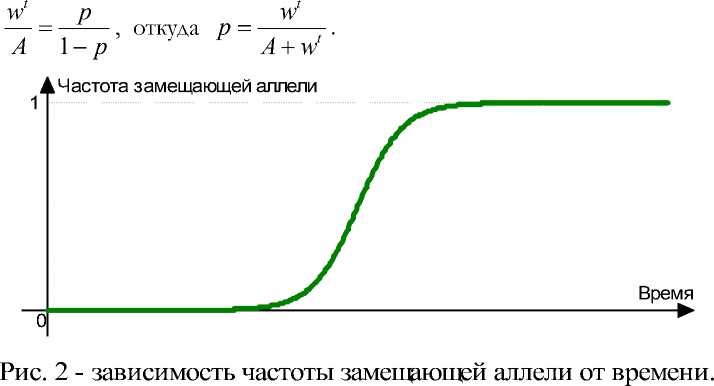
Из графика на рис 2 видно, что б о льшую часть времени Т , в течение которого в генофонде популяции есть и замещаемые, и замещающие аллели, частоты аллелей почти не изменяются.

Пусть в момент времени tI частота замещающей аллели равна а, пусть в момент

w^{t 1}

Тогда ----- = a

A + w^{t |}

1 2 частота принимает значение b ( а меньше b ).

, b(I - a) ln w2                                  a (I - b)

и ------ — = b , откуда A t = t₉ - t =----------

A + wt 2                21 In w

- т.е. время, за которое частота замещающей (отбираемой) аллели изменится от а до b , от численности популяции не зависит.

T 2ln A

Отношение же — = —77;---7 , показывающее, во сколько

A t ln b ^{(| -} a )

a (I - b )

раз время, за которое частота замещающей аллели изменится от a до b , меньше времени, в течение которого в генофонде популяции будут встречаться и замещаемые, и замещающие аллели, не зависит от относительной приспособленности. Т.е., например, если численность какой-то панмиктической гаплоидной популяции составляет миллион особей, то время, за которое частота любой фенотипически полезной аллели изменится, скажем, от 0,05 до 0,95 , будет

2ln1000000

в —   ,—   . «4,7 раза меньше, чем время, за которое l 0,95(1 — 0,05)

n 0,05(1 - 0,95)

частота этой же аллели изменится от нуля до единицы.

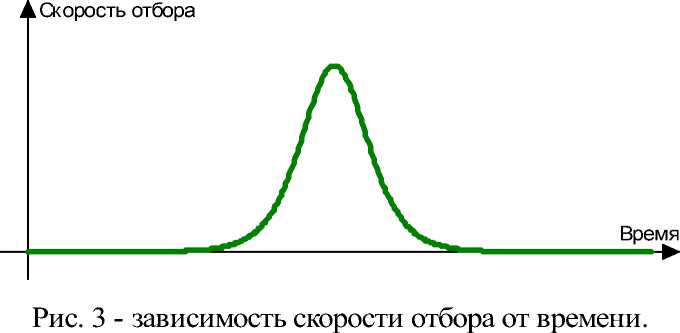
Очевидно, производная по времени от p – это скорость отбора:

v = p =

w^t ln w   w ^{2 t} ln w

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^  ^^^^H ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^~

A + W (A + W )2 '

Из графика на рис 3 видно, что б о льшую часть времени Т , за которое одна аллель полностью замещает другую, скорость отбора почти нулевая.

wt

Учитывая, что p =----- , можно найти зависимость скорости

A + W отбора от частоты замещающей аллели:

v = p In w — p ² In w

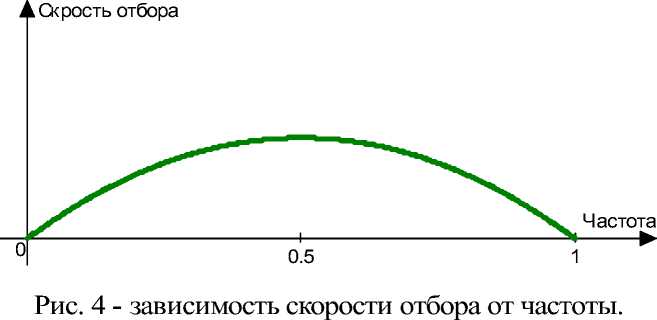
Из графика на рис 4 видно, что скорость отбора минимальна, когда частота находится возле нуля или единицы, и максимальна, когда частота равна 0,5 – что, впрочем, давно известно.