Простой способ генерации поляризационно-неоднородного лазерного излучения, основанный на применении ДОЭ

Большинство современных лазеров производят поляризационно-однородное излучение, т.е. поляризационные параметры во всех точках поперечного сечения лазерного пучка одинаковы. Однако с помощью дополнительных внутри- или внерезонатор-ных устройств возможно формирование множества различных типов векторных поляризационнонеоднородных мод с уникальными свойствами.

Наибольший практический интерес представляют пучки, имеющие аксиальную симметрию всех параметров лазерного излучения, включая поляризацию, например, пучки с радиальным и азимутальным направлением поляризации.

Цилиндрические (с аксиальной симметрией) векторные пучки имеют множество приложений, включая микроскопию, литографию, ускорение электронов, обработку материалов, высокоразрешаю щую метрологию, микроэллипсометрию и спектроскопию. Подробный обзор приведён в работе [1].

При острой фокусировке радиально-поляризованного пучка в фокусе возникает мощная продольная компонента электрического поля, а вклад поперечных компонент на оптической оси нивелируется. Данный эффект используется для уменьшения размеров фокального пятна [2-7], для оптического захвата и трёхмерного ориентирования молекул [8-11], а также для ускорения электронов [12, 13].

По сравнению с обычной (линейной или круговой) поляризацией радиально-поляризованный пучок имеет удвоенную эффективность при резке металлов [14], также высокий уровень поглощения, характерный для этого типа поляризации, используется при взаимодействии лазерного излучения с плазмой [15]. C другой стороны, при прохождении через полые металлические волноводы радиально-поляризованные пучки демонстрируют большие потери энергии на стенках волновода, а азимутально-поляризованные пучки, соответственно, минимальные [16].

Известны схемы генерации аксиально-поляризованных пучков с использованием конической приз- мы Брюстера [17], сегментированных волновых пластинок [4, 18], дифракционных зеркал с высокой локальной поляризационной селективностью [19], субволновых диэлектрических решёток [20]. Также можно использовать свойства двулучепреломления внутренних лазерных кристаллов [21, 22] или применить в качестве выходного зеркала резонатора специальное фотонно-кристаллическое зеркало [23]. Перечисленные схемы можно условно отнести к внутрирезонаторным.

Главным преимуществом внерезонаторных методов для формирования поляризационно-неоднородных мод является универсализм. Внерезонаторные методы, как правило, основаны на когерентной суперпозиции пары обычных мод, например, с помощью интерферометра. Таким способом можно формировать любые типы векторных пучков, и, в принципе, такой метод применим для любой длины волны. Кроме интерференционных методов [24-27] известны схемы с использованием маломодовых оптических волокон [28, 29] и нематических жидкокристаллических пространственных модуляторов света [30-32].

Интерференционные методы основаны на использовании в качестве входного излучения одной моды, полученной, как правило, внутрирезонатор-ным способом. Схема получения второй моды, взаимно когерентной с исходной, но с другой поляризацией, довольно сложна в настройке, т.к. необходимо точное совмещение полей мод и создание необходимых фазовых сдвигов между модами. Также в этом случае используется большое количество сложных элементов типа призмы Дове, поляризационных разделительных призм, 90-градусного перископа и др. [24-27].

При использовании оптических волокон обычн о возбуждается целая группа мод и, чтобы выделить какую-то одну из них, необходимо подавать на вход волокна излучение с определённой поляризацией, специальным образом сдавливать волокно или изменять его длину с высокой точностью [28, 29]. Всё это не лучшим образом сказывается на эффективно- сти и «чистоте» поляризационного состояния выходного п учка.

Применение же жидкокристаллических дисплеев при всей универсальности [30-32] характеризуется локально-матричной структурой с довольно грубым разрешением и низкой энергетической эффективностью. Кроме того, для жидкокристаллических пространственных модуляторов света имеется взаимосвязь фазовых и поляризационных изменений, что требует дополнительного оптимизационного кодирования.

Применение дифракционных оптических элементов (ДОЭ) даёт возможность избежать этих сложностей, поскольку методы дифракционной оптики позволяют получать из основной моды лазера любые другие моды в разных плечах оптической схемы с высокой эффективностью.

В работах [33, 34] предложена и экспериментально апробирована новая оптическая схема для суммирования двух световых полей с произвольными комплексными коэффициентами при помощи дифракционной решётки, используемой в качестве фильтра в двухкаскадной системе с одновременным Фурье-преобразованием исходных полей. Модовые пучки формируются с помощью ДОЭ, аналогичных рассмотренным в [35, 36].

Использование ДОЭ для формирования лаз ер-ных полей обеспечивает простоту и универсальность конвертации. Универсальность со стоит в возможности мет одам и дифракционной оптик и производить п ракти чески любые зад а ваем ые распределения полей из фундаментального лаз ерно го излучения, т.е. в суперпозиции могут участ в о ват ь любые лазерные п учки . Такж е использование фазовой диф ракци онной решётки в ка чест ве с вето-делительного элемента позволяет мен ят ь межмо-до вый фазовый сдвиг без применения доп олни-тельн ых элементов.

Однако предложенное в [33, 34] устройство имеет большие габариты и вес за счёт наличия двух оптических Фурье-каскадов, причём фокусные расстояния линз, расстояние между суммируемыми модами и период дифракционной решётки должны быть точно согласованы между собой. Наличие двух линз приводит к дополнительным потерям световой энергии. Кроме того, во избежание искажений суммируемых мод апертуры этих линзы должны быть существенно боль ше размеров мод. Это связано с тем, что моды изначально децентрированы по отношению к линзам, что является неустранимой особенностью данной схемы.

В данной работе рассмотрено устранение указанных недостатков при сохранении достоинств данной оптической схемы, которое осуществлялось за счёт использования таких возможностей ДОЭ, как формирование заданного распределения в нескольких дифракционных порядка х за счёт кодирования ДОЭ с несущей частотой [37]. В этом случае комплексные распределения в симметричных порядка х дифракции складываются на некотором расстоянии от плоскости ДОЭ, позволяя исключить из оптической схемы линзы.

1. Описание упрощённой схемы поляризационного конвертора на основе ДОЭ

Уменьшение габаритов и веса оптической системы, а также снижение потерь световой энергии возможно за счёт исключения из оптической схемы линз. Также это даст уменьшение числа согласуе-мых параметров, а значит, и упрощение настройки. Функции линз должны взять на себя сами ДОЭ. Линзы могут быть исключены из оптической схемы, если формирующие моды ДОЭ выполнены в виде цифровых голограмм с несущей частотой. Такие голограммы дают полезное распределение комплексной амплитуды в первом порядке дифракции и обеспечивают наложение мод, формируемых в +1ом и -1-ом порядках дифракции на некотором расстоянии от плоскости голограммы, то есть выполняют в данном случае одну из функций линзы. Оптическая система суммирования мод выполнена в виде дифракционной решётки с таким же углом дифракции первого порядка, как и у п учков сформированных мод. Оптическая схема экспериментальной установки показана на рис. 1.

Рис. 1. Схема упрощённого когерентного суммирования двух световых полей с произвольными комплексными коэффициентами при помощи дифракционной решётки

Лазерный источник оптического излучения с линейной поляризацией Л освещает цифровые голограммы Г1 и Г2, причём плоскости поляризации излучения формируемых мод получаются взаимно ортогональными за счёт пластинки в полволны П, расположенной перед одной из голограмм. Каждая из голограмм формирует моду в +1-ом и -1-ом порядках дифракции, которые распространяются под углами ±θ , определяемыми несущей частотой голограммы. Моды, сформированные в +1-ом порядке дифракции одной голограммой и в -1-ом порядке дифракции другой голограммой, распространяются в сходя щих-ся направлениях и попадают на дифракционную решётку Р, как показано на рис.1. Решётка Р должна быть расположена в плоскости, проходящей через точку пересечения оптических осей мод, сформированных в +1-ом порядке дифракции одной голограммой и в -1-ом порядке дифракции другой голограммой, для обеспечения совпадения оптических осей суммируемых мод. Излучение каждой из данных мод, прошедшее дифракционную решётку, в свою очередь, разделяется на дифракционные порядки, причём если период дифракционной решётки сделать равным периодам несущих частот голограмм, то +1-й дифракционный порядок решётки для одной моды и -

1-й порядок решётки для другой моды будут распространяться по нормали к плоскости решётки. Таким образом обеспечивается точное совмещение мод как по пространственному положению за счёт помещения решётки в плоскость, проходящую через точку пересечения оптических осей мод, так и по углу. Изменение межмодового фазового сдвига в оптической системе осуществляется за счёт сдвига дифракционной решётки поперёк оптической оси.

2. Описание алгоритма действия упрощённой схемы когерентного суммирования

Рассмотрим входное поле в виде двух модо вы х распределений T 1 ( x , y ) и T ₂( x , y ), симметрично сдвинутых от центра на расстояние a вдоль Каждое из распределений промодулировано кочастотной функцией:

, У) =

= [ T 1 ( x - a , y ) + T ₂( x + a , y ) ][ 1 + cos( в x ) ]

где k = 2л/ % - волновое число, % - длина волны лазерного излучения.

Интеграл (2) можно вычислить методом стационарной фазы с достаточно хорошей точностью [38]. Стационарная точка в (2) определяется из выражения:

। ^z а x, = u x, = u ± —в , ¹ . s k

в зависимости от порядка дифракции.

На некотором расстоянии z ₀ поле будет содержать 6 слагаемых:

S₁₂ = T 1 I u ± —- в- a , v I exp ^, к      2 n           )

- -k Iu ±%« в 122z I    2n )

оси х . высо-

Распространение поля (1) в свободном пространстве на расстояние z в плоскости y =0 можно описать с помощью 1D преобразования Френеля:

F (u , v , z ) =

^

J f ( x , y )exp

—^

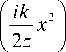
I ik   L , exp Ixu I dx

I z    )

F ( u , v , z _o ) = { T 1 ( u , v ) exp ( - i в u ) + T ₂ ( u , v ) exp ( i в u ) } exp

+{T1 (u - a, v) + T2 (u + a, v)} exp

+ {T 1 ( u - 2 a , v ) exp

-

S 3 = T 1 ( u - a, v ) exp

ik ₂ u

2 z

S45 = T 2I u ± —0 в + a, v I exp , к 2n )

S 6 = T ₂ ( u + a , v ) exp

ik ₂ u

2 z

ik ₂

--u

2 z 0

+

-^- (u + a )2 + T2( u + 2 a, v) exp 2 z'

-

- iL Iu ±%o в) 2z к     2n )

%z

При a = —⁰ в на этом расстоянии в нулевом по-2 п

рядке произойдёт сложение S ₁ и S ₅ :

-

ik 2 z 0

u

+ a2)

ik 2

--- u - a

2z v 7

2 z ₀

+

Если установить в плоскости z ₀ 1D дифракционную ре шётку, имеющую точно такую же частот у, как модулирую щая функция на входе:

t( u ) = [ 1 + cos ( в u + b ) ] ,                          (5)

где b – смещение решётки вдоль оси u , то после прохождения пучком (4) такой решётки нулевой порядок разделится ещё на три:

G ( u , v , z o ) ~ { T i ( u , v ) exp ( ib ) +

+T ₂ ( u , v ) exp ( - ib ) }

+{T1 (u, v) exp (- i в u ) + T 2 (u, v) exp (i в u)} +

+{T1 (u, v) exp (- i 2в u) exp (-ib) +

+T ₂ ( u , v ) exp ( i 2 в u ) exp ( ib ) } .

Таким образом, в нулевом порядке будет формироваться суперпозиция двух модо вых распределений:

G o ( u , v , z o ) ~ c T i ( u , v ) + ^ 2 ( u , v ) ,                 (6)

где c = exp ( i 2 b ) - комплексная константа, пропорциональная сдвигу ре шётки в плоскости z ₀ .

Установка полуволновой пластинки на пути формирования одного из модовых п учков, например, как показано на рис. 1, позволяет выполнить сложение пучков с ортогональными поляризациями:

G o ( ^u , ^v , ^z o ) ~ c ^T 1 ( ^u , ^v ) e x + ^T 2 ( ^u , ^v ) e y .           (7)

При различных значениях коэффициента и участвую щи х в с уперпозициях мода х формируются различные типы поляризаций, в основном смешан- ные, но можно получить радиальную и азимутальную [33, 34].

Таким образом, модулирующая функция в (1) и дифракционная решётка (5) должны быть согласованы по частоте в (в обратных единицах длины). Период решётки определяется по формуле: d = 2л/ в .

Расстояние установки дифракционной решётки определяется периодом решётки и расстоянием между ДОЭ, формирующими модовые пучки:

ad

z» =

o %

.

Аккуратно выполнить размещение ДОЭ на входе можно при записи их на одной подложке. В этом случае совмещение пучков в плоскости (8) осуществляет- ся с высокой точностью без кропотливой юстировки. Остаётся лишь точно выставить подложку с ДОЭ так, чтобы прямая, соединяющая их центры, была перпендикулярна штрихам дифракционной решётки. Это также не вызывает трудностей, поскольку осуществляется вращением всей подложки с ДОЭ в целом, с контролем совмещения полей лишь по одной координате. Подбор необходимых фазовых сдвигов между световыми полями также существенно упрощается, поскольку используются дифракционные решётки, период которых на один – два порядка больше λ, и соответственно, на порядок снижаются требования к точности юстировки соответствующего элемента.

• 3.    Синтез ДОЭ и результаты моделирования

Для расчёта фазовых ДОЭ, формирующих модовые пучки Гаусса-Эрмита (ГЭ), модулированные высокочастотной функцией, был использован метод частичного кодирования [39, 40].

На рис. 2 а показана фаза ДОЭ, предназначенного формировать пару мод ГЭ с индексами (0,9), распространяющихся под углами к оптической оси. На рис. 2 б показано рассчитанное распределение интенсивности, формируемое этим ДОЭ на расстоянии z=500 мм от плоскости ДОЭ.

Моделирование когерентного сложения двух модовых пучков, распространяющихся под углами к оптической оси, показано на рис. 3. На рис. 3 а приведён вид подложки, на которой располагаются два фазовых ДОЭ, формирующих моды Г Э с индексами (0,9) и (9,0), соответст венно. На рис. 3 б показано рассчитанное расп ределение интенси вно-сти, формируемое на расстоянии z=250 мм от плоскости ДОЭ. Как видно из рисунка , симметричные ди фракционные порядки с различными мо да-ми накладываются друг на др уга в плоскости, находящейся на расстоянии (8) от ДОЭ, в соот ветст-вии с выражением (4).

б)

Рис. 2. Формирование мод ГЭ (0,9), распространяющихся под углами к оптической оси: (а) фаза частично кодированного

ДОЭ, (б) распределение интенсивности (негатив), рассчитанное на расстоянии z=500 мм от плоскости ДОЭ

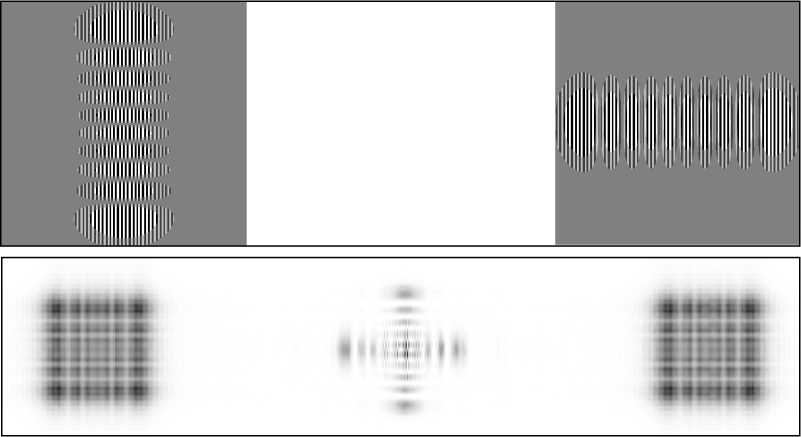
Рис. 3. Моделирование схемы когерентного сложения двух мод ГЭ (0,9) и (9,0): (а) вид фазы двух ДОЭ, расположенных на одной подложке, (б) распределение интенсивности (негатив), рассчитанное на расстоянии z=250 мм от плоскости ДОЭ

• 4.    Экспериментальное формирование поляризационно-неоднородных пучков

Точное соответствие частоты дифракционной решётки несущим частотам цифровых голограмм достигается за счёт того, что как цифровые голограммы, так и дифракционная решётка изготовляются, как правило, в одном технологическом цикле и достижение точного соответствия их параметров не представляет сложности.

На одну подложку были записаны три пары бинарно-амплитудных ДОЭ, формирующих моды ГЭ с индексами (0,n) и (n,0) при n=1, 4, 9 (см. рис. 4).

Запись выполнялась при помощи кругового лазерного записывающего устройства CLVS-200. Каждый ДОЭ имел размер 2 x 2 мм с несущей частотой около 30 лин/мм, расстояние между парными ДОЭ составляло 12 мм. По той же технологии, но на другой подложке была изготовлена соответствующая дифракционная решётка.

моды ГЭ с индексами (0,n) и (n,0) при n=1, 4, 9

В оптической схеме, представленной на рис.1, в качестве лазера Л использовался гелий-неоновый лазер ЛГН-215. Расширитель пучка включал 8Х микрообъектив, диафрагму 50 мкм и коллимирующий объектив с фокусным расстоянием 300 мм. Параметры собранной оптической схемы были выбраны близкими к соответствующим параметрам оптической схемы, описанной в [33, 34], для получения сравнимых результатов.

На рис. 5 показаны результаты экспериментального когерентного сложения мод ГЭ (0,4) и (4,0) (рис. 5 а, б) и мод ГЭ (0,9) и (9,0) (рис. 5 в, г ) с различными коэффициентами с использованием оптической схемы, приведённой на рис. 1.

Для мод ГЭ (0,1) и (1,0) данная схема позволяет легко получать лазерные пучки с радиальной и азимутальной поляризацией [41, 33, 34].

Полученные результаты при отсутствии анализатора в оптической схеме и его различных положениях приведены на рис. 6, 7.

Сравнение их с результатами, приведёнными в [33], показывает более высокое качество формирования мод и, соответственно более высокое качество выходного п учка с требуемыми поляризациями.

Это объясняется большей устойчивостью к шумам бинарно-амплитудных голограмм, работаю щи х в первом порядке дифракции. Несмотря на низкую энергетическую эффективность бинарно-амплитуд- ных голограмм, общая энергетическая эффективность оказывается сравнимой с [33] из-за отсутствия двух объективов.

Однако в процессе юстировки модифицированной оптической системы были выявлены более высокие требования к кривизне волнового фронта пучка, освещающего голограммы, чем ранее в [33]. Это связано, очевидно, с возможностью частичной компенсации расходимости освещающего пучка в [33] за счёт смещения плоскости расположения ДОЭ от фокальной плоскости Фурье-преобразующего объектива, что по понятным причинам невозможно во вновь предложенной схеме. Однако при правильной юстировке коллиматора по картине интерференции пучков, отражённых от поверхностей наклонной плоскопараллельной пластины, никаких проблем, связанных с расходимостью освещающего пучка, не возникает.

Исследования также показали весьма высокую чувствительность предложенной оптической системы к отклонениям параметров дифракционной решётки от заданных. Так, несмотря на близость периода решёток в данной работе и работе [33] (отличие не более 5%), применение решётки из [33] приводит к полному разрушению поляризационной структуры пучка. Данное свойство оптической системы, однако, не является недостатком, так как требуемые параметры легко могут быть получены при изготовлении решёток в едином расчётном и технологическом цикле.

Заключение

Таким образом, предложена и экспериментально исследована новая оптическая система для генерации поляризационно-неоднородного лазерного излучения, основанная на применении ДОЭ с несущей частотой. Данная система содержит меньше оптических элементов и проще в настройке, чем ранее исследованная, включавшая линзы. При необходимости энергетическая эффективность формирования пучков может быть повышена п утём замены амплитудных голограмм на фазовые.

• б)-------------------- в)

Рис. 5. Результаты экспериментального когерентного сложения мод с различными коэффициентами с использованием оптической схемы, приведённой на рис. 1: а) и б) для мод ГЭ (0,4) и (4,0), в) и г) для мод ГЭ (0,9) и (9,0)

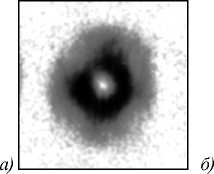
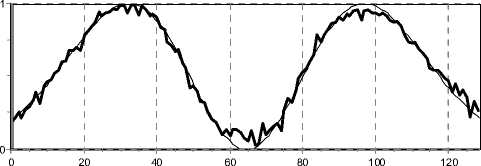
Рис. 6. Распределение интенсивности на выходе оптической схемы для мод ГЭ (0,1) и (1,0): (а) экспериментальная картина (негатив) и (б) сравнительное продольное сечение - экспериментально полученное (толстая линия) и теоретическое (тонкая линия)

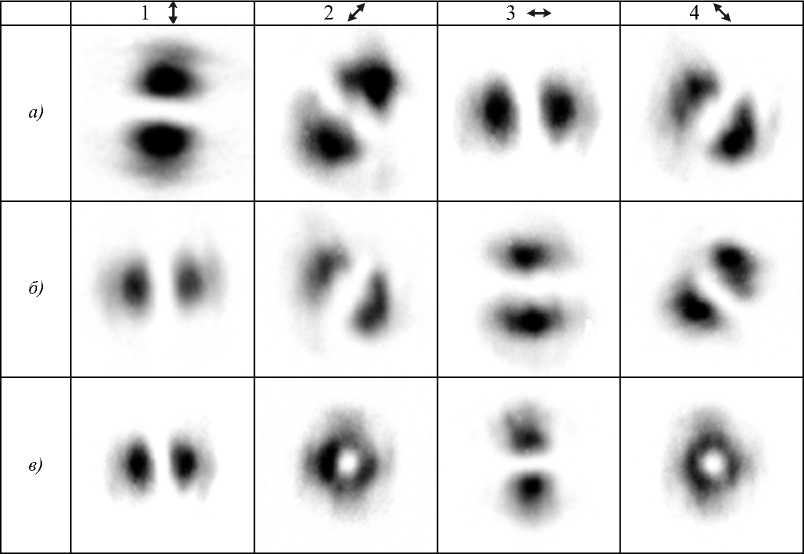
Рис. 7. Распределения интенсивности (негатив) на выходе оптической схемы при различных положениях анализатора (1 - вертикальное расположение, 2 - повёрнутое вправо на 45 ° 3 - горизонтальное положение, 4 - повёрнутое влево на 45 ) для различных суперпозиций изначально линейно-поляризованных мод ГЭ (0,1) и (1,0): (а) радиальная, (б) азимутальная, (в) смешанная линейно-круговая поляризации

Полученные экспериментальные результаты показали более высокое качество формирования пучков с неоднородной поляризацией, чем в ранее предложенной системе.

С другой стороны, предложенная оптическая схема открывает широкие возможности по миниатюризации оптической системы, а также упрощению технологии сборки и настройки, так как не содержит оптических элементов в объёмном исполнении, все расстояния и положения элементов заранее известны, а для получения какой-то одной заданной поляризации (например, радиальной) вообще не требует настройки. Всё это даёт возможность в перспективе реализовать данную оптическую систему в интегрально-оптическом исполнении.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и выс шее образование» (грант CRDF PG08-014-1), грантов РФФИ 10-07-00109-а, 10-07-00438-а и гранта Президента РФ поддержки ведущих научных школ НШ-7414.2010.9.