Пространственная фильтрация гармоник когерентного излучателя

ПРОСТРАНСТВЕННАЯ ФИЛЬТРАЦИЯ ГАРМОНИК КОГЕРЕНТНОГО ИЗЛУЧАТЕЛЯ

В [1,2] для выделения излучения лазерных гармоник области вакуумного ультрафиолета (ВУФ) из спектра гармоник предложен пространственный фильтр (ПФ), состоящий из зонной пластинки (ЗП) с определенным образом выбранным числом зон и диафрагмы, расположенной в главном фокусе ЗП, для длины волны выделяемой гармоники, и показано, что в случае целочисленных гармоник выбором числа зон ЗП можно обеспечить условия оптимальной фильтрации. Предлагаемый метод фильтрации может быть использован для выделения гармоники высшего порядка в источниках когерентного излучения ВУФ-диапазона с каскадным умножением частоты (см. [3,4]), когда традиционные методы фильтрации, основанные на применении поглощающих фильтров, призм и дифракционных решеток, могут оказаться непригодными из-за сильного поглощения ВУФ-излучения различными средами, а также невозможности работать в фокусированных пучках.

В настоящей работе исследован общий характер зависимости эффективности фильтрации от параметров ПФ и исходного дискретного спектра длин волн.

Пусть на ЗП падают две плоские монохроматические волны А и А', причем выделению подлежит волна А. Для расчета условий и эффективности оптимальной фильтрации воспользуемся формулой для распределения ампли туды волны вблизи оси ЗП при нормальном падении на нее плоской монохро матической волны А единичной амплитуды [5] :

A(x,r) = Е i0(-r-rsin у )ехр 1(-г- R + m п) m-0 А          "I I л где:

• х - координата на оси ЗП;

• г - расстояние от оси ЗП;

• R = /х²+р²; m        m

Pm = /т A L - радиус т-й эоны ЗП;

• L - главное фокусное расстояние;

1о(^Дгз1п у ) - функция Бесселя нулевого порядка; л        т

• Y_m - угол, под которым виден радиус т-й эоны из рассматриваемой

точки на оси ЗП;

• N - полное число зон ЗП.

Формула (1) получена для ЗП с первой прозрачной зоной и нечетным полным числом зон в приближении малых углов у . Тогда в плоскости главного фокуса волны А распределение амплитуды волны А' имеет вид:

A'(L,r) = exp(i ^ L) S 1 0 (2п Г-p /"^ ) x m=0

X

exp imn(l

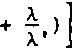
Введем безразмерный параметр X = 1,22 r/6R0 ,

(XL/N)2 - радиус главного фокуса волны в сечении,

где 6 Ro = 0,61

перпендикулярном

оси ЗП. В этом случае (2) принимает вид:

A' (L,x) = exp(i ^L) S Io(nx;, j * Л m=0        A

* exp lmn(l +

причем в точке главного

фокуса волны X

A'(L,0) = ехр(1 $ L)

N

S exp i m п (1 ш=0

exp(i ту L)

exp[i(N+l) (1+ р-ехр [^1(1 + ^г)т1

Из формулы (3) следует, что распределение амплитуд волн А и Л1 в плоскости главного фокуса волны X определяется лишь отношением Х/Х’, числом зон ЗП и диаметром фильтрующего отверстия. Формула (4) дает пра вило выбора зон ЗП. Очевидно, фильтрация будет происходить с максимальной эффективностью, если полное число эон ЗП таково, что A'(L,0) имеет минимально возможное значение. Если длины волн X и X1 относятся как р/n, где р и п - целые числа, амплитуда A1 (L,0) обращается в нуль при N = 2qn - 1 (гае q = 1,2,... ) для всех X < X1 , а также для X > X' за исключением случаев, когда Х/Х* # 2g - 1, гае g = 1,2,3,... .При Х/Х* = 2g - 1 главный фокус волны X совпадает с дополнительным фокусом (Е + 1) - порядка волны X1, как следует из (4), амплитуды обеих волн в этой точке равны (N + 1) . Поперечные размеры фокусов различны и определяются формулой (3). Если исходное излучение состоит из дискретных компонент, связанных отношением целых чисел, то амплитуды всех волн Л1 кроме минимальной X . , подлежащей выделению, обращаются в нуль в точке главного фокуса min волны X , при mln

N = 2qs - 1,                                                                  (5)

где s - наименьший общий знаменатель дробей Wx'-

Таким образом, предлагаемый ПФ может быть использован для выделения гармоник дробного порядка, которые, например, могут возникать при взаимодействии мощного лазерного излучения с плазмой [б] .

На основании формулы (3) с помощью ЭВМ проведен расчет оптимальной эффективности фильтрации волны шением Xj = у, где j = 1,2,3,.

Х^ из спектра волн Xj,

связанных соотно-

..,К, которое справедливо для целочислен-

ных гармоник,

а также для дробных с

одинаковым числителем.

Согласно

в данном случае фильтрация волны Х^

будет происходить наиболее эффек

тивно,

если полное число

эон зонной пластинки удовлетворяет соотношению

N = 2qk - 1.

Поскольку на входе ПФ все волны имеют единичную амплитуду,

эффективность фильтрации

nkj волны Х^ от волны Х^ определяется отноше

нием потоков энергий этих волн за диафрагмой ПФ, т.е.

nkj(Xo)

X

/ A=(x)XdX

X

/ A?(x)XdX о 3

где

Хо - радиус диафрагмы.

Расчет показал, что эффективность фильтрации волн Х^ с к ^ пластинкой с N ~30 уже более 103 и растет с номером выделяемой ники. На рис. 1 приведены зависимости эффективности фильтрации

3 зонной

гармо-

nkj для

к - 3 и j = 1,2 от радиуса диафрагмы ПФ. Аналогичные зависимости для к = 4 и j = 1, 2, 3 приведены на рис. 2.

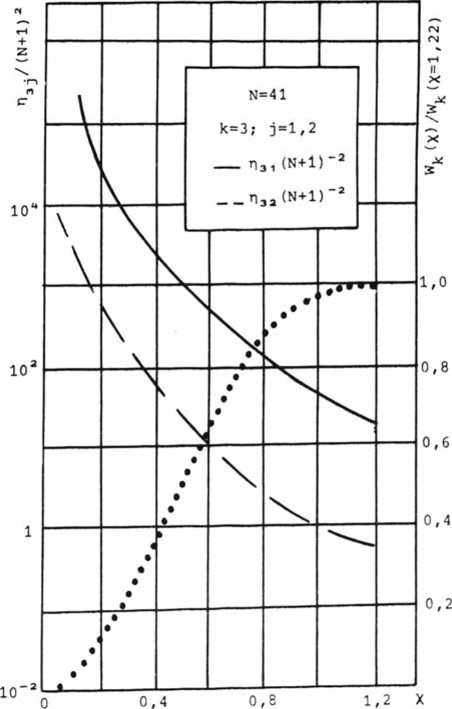
Рис. 1. Зависимость приведенной эффективности Из и мощности W3 выделяемой третьей гармоники (из спектра гармоник первого и второго порядков) в зависимости от радиуса диафрагмы х

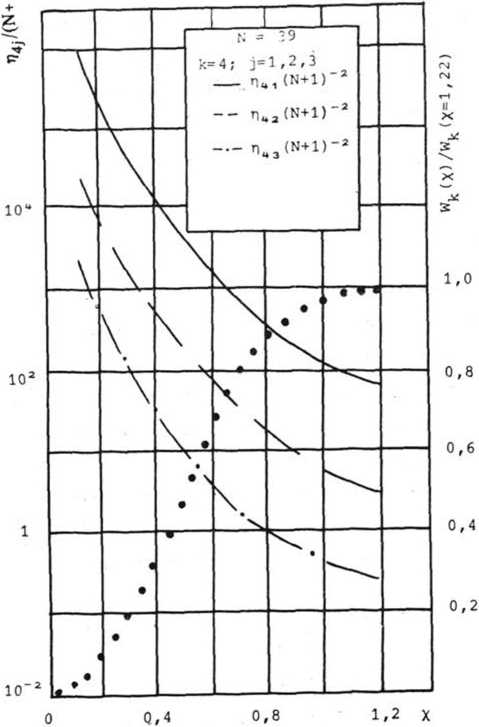
Рис. 2. Зависимость приведенной эффективности Пи и мощности Мц выделяемой четвертой гармоники (из спектра гармоник первого, второго и третьего порядков) в зависимости от радиуса диафрагмы X

Как следует из рисунков 1 и 2, эффективность фильтрации высших гармоник резко растет с уменьшением диаметра диафрагмы. Расчет показал также, что для 0 < X S 1,2 распределение квадрата амплитуды j-й гармоники А^(х, N) в плоскости диафрагмы ПФ практически не зависит от полного числа зон для N > 30. Таким образом, для отношения эффективностей фильтрации двух зонных пластинок с числом зон Ni и Na > 30 с большой степенью точности справедливо соотношение nkj(X' Nl) _ , N, + 1 2

nkj(X, N2) V N3 + 1' 1

Формула (6) связывает основные характеристики различных ПФ и поэво ляет вычислить эффективность фильтрации любого ПФ по известным характе ристикам конкретного.

Экспериментальная проверка предложенного метода фильтрации проводилась на 2-й и 3-й гармониках неодимового лазера, которые получались каскадным преобразованием основного излучения (X = 1,064 мкм) в кристаллах КОР. Основное излучение лазера и двух его гармоник направлялись на ЗП с N = 41, изготовленную фотолитографическим способом. В точке главного фокуса ЗП (Хз = 1 м) для излучения третьей гармоники помещалась диафрагма диаметром 100 мкм. Полученные значения эффективности фильтрации составили rial ~8-103 и Пзг ~3.102, что достаточно хорошо совпадает с расчетными данными (~2.104 и ~103 соответственно).