Пространственная фокусировка второго порядка пучков заряженных частиц на краевых полях электростатического секторного сферического дефлектора с большим межэлектродным зазором

Одним из наиболее удачных решений для рентгенофотоэлектронной спектроскопии высокого разрешения стала энергоанализирующая система на основе электростатического сферического конденсатора благодаря сочетанию свойств большой энергетической дисперсии и двойной пространственной фокусировки, разделенных по энергии заряженных частиц [1, 2]. Для моноэнергетических пучков, испускаемых точечным источником, в плоскости энергетической дисперсии в идеальном центрально-симметричном электростатическом поле осуществляется фокусировка по азимутальным направлениям и угловая фокусировка по направлению первого порядка. Другим ценным свойством, существенным для возможности проведения параллельного энергоуглового анализа, является большая протяженность плоскости энергетической дисперсии сферического дефлектора, линейные размеры которой определяются величиной межэлектродного зазора. Отмеченные особенности привели к широкому распространению систем со сферическим дефлектором в аналитических приборах высокого разрешения и в физическом эксперименте в различных областях науки и технологии. Возможности улучшения характеристик энергоанализаторов этого типа и расширения их функций представляли постоянный интерес для исследователей [3–5].

Разрешающую способность по энергии ограничивает качество фокусировки, определяющее допустимую величину углового акцептанса анализи- руемого пучка и в конечном результате светосилу энергоанализатора [6, 7].

В настоящей работе с помощью компьютерного моделирования исследовалась возможность получения в секторных сферических энергоанализаторах с большим межэлектродным зазором фокусировки более высокого порядка, чем первый. На основе анализа влияния на фокусировку линзовых эффектов в межэлектродном зазоре и исследования характеристик энергетических распределений частиц вместо применяемого обычно рассмотрения электронно-оптических аберраций искались условия решения поставленной задачи.

МОДЕЛЬ СФЕРИЧЕСКОГО ДЕФЛЕКТОРА С БОЛЬШИМ МЕЖЭЛЕКТРОДНЫМ ЗАЗОРОМ

Для описания движения заряженных частиц в центрально-симметричном поле сферического конденсатора применена модель (см. рис. 1), определяемая следующими параметрами: r 1 , V 1 — радиус и потенциал внутренней сферы; r 2 , V 2 — радиус и потенциал внешней сферической обкладки. Потенциал поля внутри межэлектродного зазора в точке, удаленной от общего центра сфер на расстояние r , определяется из уравнения

V r = ( V 2 - V 1 ) r ₂ , (1 - r i ) + v 1 .        (1)

r ₂ - r 1           r

Точечный источник S ₁ моноэнергетических нерелятивистских заряженных частиц расположен

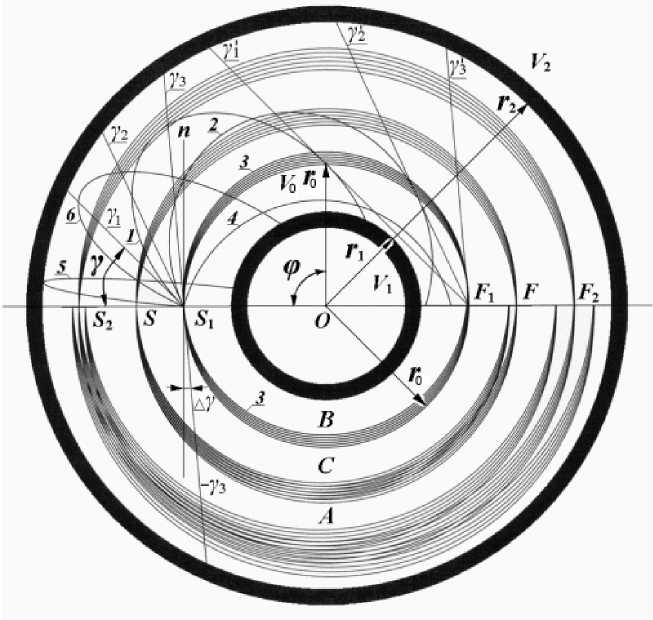
Рис. 1. Модель идеального сферического дефлектора.

r о — радиус эквипотенциальной поверхности V ₀ = 0; r i , V ₁ — радиус и потенциал внутренней сферы; r ₂, V 2 — радиус и потенциал внешней сферической обкладки; О — общий центр сфер; r ₂ = 2 r ₀, r ₂ = 3 r ₁;

В , С , А — семейства траекторий моноэнергетических частиц, испускаемых точечными источниками в позициях S ₁, S , S ₂ соответственно; кинетические энергии движения по круговой орбите возрастают в последовательности В >  С >  А ;

F 1, F, F2 — области фокусов этих траекторий на оси симметрии; семейство В содержит группу траекторий с произвольными углами вылета Y (Y ь Y2, Y3) из источника S 1; углы у^,Y2',Y3' соответствуют касательным к траекториям с углами у 1, Y2, Y3 в точках пересечения с эквипотенциальной поверхностью V0 = 0; ф — полярный угол между радиальными направлениями к точкам пересечения траекторий с углом вылета y эквипотенциальной поверхности V0 = 0; семейство С содержит группу траекторий частиц с кинетической энергией меньше на 1 % энергии в основной группе; семейство А состоит из трех групп траекторий частиц одинаковой энергии — основной и двух дополнительных с точками старта с оси справа и слева от основной на пересечении эквипотенциальной поверхности V0 радиуса r0 с осью симметрии сферических обкладок. Частицы c одинаковым знаком заряда q приобретают начальную скорость v0 и кинетическую энергию W при прохождении в источнике ускоряющей разности потенциалов U:

W = qU = mv²- . (2)

Ось пучка перпендикулярна оси симметрии и направлена по касательной к эквипотенциальной поверхности V ₀. К обкладкам приложены равные по абсолютной величине, но противоположные по знаку потенциалы: V ₂ — отражающий частицы, V ₁ — притягивающий; потенциал V ₀ = 0. При этих условиях из соотношения (1) устанавливается взаимосвязь величин радиусов обкладок r i , r 2

и позиции источника r 0 , определяющих геометрию системы. Если взять r ₂ = 2 r ₀, из (1) следует, что r 2 = 3 r 1 , а источник удален от общего центра O сферических обкладок на расстояние 1.5 r 1 .

Частицы, следующие из источника по траекториям, исходящим под произвольным углом γ между направлением скорости и нормали к поверхности эквипотенциали V 0 в области над эквипотен-циалью, будут испытывать торможение в радиальном направлении движения до точки перегиба траектории в позиции r max , соответствующей максимальному удалению от общего центра сфер (например, траектории 1–6 в верхней части рис. 1 над осью S 1 О ). Напротив, частицы, стартующие из источника асимметрично, с внутренней стороны эквипотенциальной поверхности, с такой же скоростью и под тем же углом между направлением скорости и нормали к поверхности (траектории семейства B в нижней части рис. 1 под осью S 1 О с углами вылета А у в пределах от нормали n к оси до углового направления – γ 3 , γ 3 ) будут двигаться в области под эквипотенциалью V ₀ с ускорением до точки перегиба траектории в позиции r min , соответствующей минимальному расстоянию до центра сфер.

Рассмотрим отдельно движение частиц в области над эквипотенциальной поверхностью V ₀ . При прохождении по траектории до точки перегиба полная энергия заряженной частицы уменьшается на величину qV r , где V r — потенциал поля внутри промежутка r ₂ r ₀. С учетом заданной конфигурации потенциалов

В соответствии с законом сохранения момента количества движения в поле центральных сил

V t = r ⁰ v о sin у .                 (5)

r

Используя (5), из уравнения (4) получим dr dt

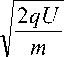
1 - (—sin у )² r

V 2 (1 - r ⁰) r

U (1 - r ⁰) r ₂

Предельное значение r _max определяется из условия v_r = 0 в верхней точке траектории.

Из (6) следует

Vr   r ²     Vrr

22    ) max ।     2 2 max - - sin у = 0

^{U ( r} 2 ^{- r} 0 ) —    ^{U ( r} 2 ^{- r} o ) r o

Корнем этого уравнения является

r max

Г Г, L ■ 2 B - 1 — 1 + .. 1 - 4sin ² у—— 2 V B²

V 7

где

B =    V 2 ^r2    .

^{U ( r} 2 ^- r 0 )

Дифференциальное уравнение, устанавливающее связь между полярными координатами r и ф , имеет вид

Vr=      -(1 - Ч r2 - r0     r

Из закона сохранения энергии следует:

dm dr

sin у

r /(1 - B) r0- + B — - sin2 у r02      r0

2 mv ₀ mv ₁ ²

= qV r ,

где v 1 = Vv - - v .2 — скорость в точке, отстоящей

Производя интегрирование в пределах от r ₀ до r _max , найдем полярный угол, на который поворачивается радиус-вектор при движении точки по траектории от источника до r _max :

от центра системы на расстояние r; vr и vτ — радиальная и касательная составляющие вектора dr скорости. В полярной системе координат v = —, dt

ф

r max

= arccos

dm vT = г—, т     dt

где ф — полярный угол. Уравнение

1 - zsin- Y B

L , B - 1.2 _л 1 - 4-----sin у

B

движения в этой области для нерелятивистских частиц будет иметь вид [8]

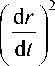
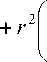
d m d t

= 2q ( U - V ) .       (4)

m

Полученные в рамках модели аналитические выражения позволяют точно рассчитать движение нерелятивистских частиц в межэлектродном зазоре идеального сферического дефлектора. При наличии на обкладках электрических потенциалов, обеспечивающих равенство ускоряющей частицы разности потенциалов U отклоняющему потен-

циалу V ₂ , все частицы с одинаковым знаком заряда, исходящие из источника в различных азимутальных направлениях по касательной к поверхности эквипотенциали V ₀ , будут двигаться по круговым траекториям радиуса r ₀ с общим центром в центре сфер, образуя в оппозитном источнику положении точечный фокус на оси системы. Детали картины движения частиц в поле дефлектора характеризуют изображения траекторий на рис. 1, на котором показаны три семейства траекторий В , С и А моноэнергетических частиц, испускаемых точечными источниками S ₁, S , S ₂, находящимися в разных позициях на оси симметрии системы. Кинетические энергии частиц, соответствующие движению по круговым орбитам в эквипотенциальных поверхностях электростатического поля, возрастают с уменьшением радиуса их орбит в последовательности В >  С >  А . Траектории частиц, стартующих с оси симметрично, с малым углом разлета относительно направления движения по круговой траектории (совпадающим с нормалью к оси n ), пересекая эту траекторию, формируют фокус первого порядка. Для симметричных начальных угловых направлений движения частиц из источника относительно круговой траектории каустика фокуса имеет наименьшее сечение на оси симметрии системы. Области F и F 2 отображают положение фокусов таких траекторий на оси. Семейство С содержит группу траекторий частиц с кинетической энергией меньше на 2 % энергии в основной группе и характеризует дисперсию по энергии системы с центрально-симметричным электростатическим полем. Из приведенного на рисунке примера следует, что энергетическое разрешение в основном ограничивают аберрации, обусловленные неидеальностью фокусировки по угловым направлениям.

При асимметричном вводе частиц каустики фокусов будут вне оси. Соответствующую этому случаю картину движения характеризует группа траекторий 1–6 семейства В с произвольными углами вылета γ (γ1, γ2, γ3) из источника S1 и фокусом в области F1. Для частиц, стартующих из источника с углами γ < π2 , траектории на начальных участках движения проходят над круговой, пересекая ее в точках выше оси. Полярный угол ϕ между радиальными направлениями к точкам пересечения траекторий с эквипотенциальной поверхностью V0 = 0 имеет величину меньше π (случай движения по круговой траектории) и равен удвоенному углу γ (ϕ = 2γ ). В результате фокус претерпевает сдвиг. Касательные к траекториям с произвольными углами вылета из источника γ1, γ2, γ3 в точках пересечениях с эквипотенциальной поверхностью V0 = 0 сходятся в точку на пересече- нии круговой траектории с осью, составляя с осью углы γ1' ,γ2' ,γ3' , соответственно равные углам вылета частиц из источника. При отсутствии под эк-випотенциалью V0 = 0 поля такие траектории образуют в точке F1 идеальный фокус [9].

Дополнительные группы траекторий частиц одинаковой энергии в семействе А с точками старта на оси справа и слева от основной, соответствующей движению по траекториям, имеющим точки старта и финиша на эквипотенциальной сферической поверхности, отображают влияние на характер движения напряженности электростатического поля в межэлектродном зазоре. Частицы, стартующие в направлении нормали к оси под эквипотенциальной поверхностью, имеют дефицит кинетической энергии для осуществления движения по круговым траекториям. Их траектории будут эллиптическими с точкой финиша на оси, смещенной по сравнению с точкой старта ближе к общему центру системы. Напротив, частицы, стартующие над эквипотенциальной поверхностью, имеют избыток кинетической энергии, их траектории также будут эллиптическими с точкой финиша на оси, смещенной по сравнению с точкой старта дальше от общего центра системы.

Особенности движения по траекториям моно-энергетических частиц с дефицитом энергии для осуществления движения по круговым орбитам предполагают возможность получения в секторных полях более совершенной фокусировки пучка на краевом поле межэлектродного зазора аналогично тому, как действует на частицы поле обычной линзы. Результаты поиска таких конфигураций секторных полей иллюстрирует рис. 2, на котором изображены две модели полусферических дефлекторов, представляющие коаксиальную комбинацию 180° секторного сферического конденсатора с геометрией и размерами идеального дефлектора (на рис. 1) и двух полых цилиндрических линз. Линзы образованы проникновением электростатического поля конденсатора в пустое пространство между цилиндрическими электродами через кольцеобразные концентрические щели в плоских электродах, разделяющих поля дефлекторов и конфигурации цилиндрических электродов. Полусферические поверхности с потенциалами V 1 и V 0 в сочетании с плоским и цилиндрическими электродами под потенциалом V ₀ образуют первый дефлектор. Контур эквипотенциали 1 характеризует провисание поля дефлектора в беспо-левое пространство. Полусферические поверхности с потенциалами V 0 и V 2 в комбинации с плоским и цилиндрическими электродами под потенциалом U 2 образуют второй дефлектор. Контур эк-випотенциали 2 характеризует провисание поля дефлектора в пространство под потенциалом U 2 .

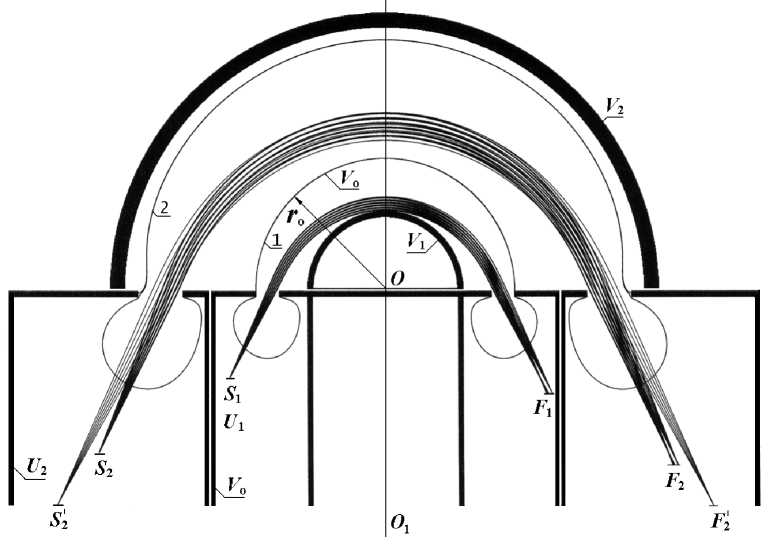
Рис. 2. Модель двух полусферических дефлекторов, представляющая коаксиальную комбинацию 180^о сектора сферического конденсатора и двух полых цилиндрических линз. Контуры эквипотенциалей 1 и 2 характеризуют провисание поля дефлектора в бесполевое пространство под потенциалами V ₀ = 0 и U ₂ соответственно.

S ₁, S ₂, S ₂ ^' — позиции точечных источников моноэнергетических частиц; F ₁, F ₂, F ₂ ^' — позиции фокусов групп траекторий частиц, исходящих из источников S 1 , S 2 и S ₂ ^' соответственно. Группы траекторий в фокусе F 1 соответствуют частицам с отличающимися на 2 % кинетическими энергиями; в фокусе F 2 энергии частиц отличаются на 1%, в фокусе F ₂ ^' сходятся траектории частиц с энергией на 7 % больше максимальной в фокусе F 2 .

При значениях потенциалов на сферических обкладках дефлекторов, соответствующих условиям модели рис. 1, структура электростатического поля на общей оси ОО 1 аксиальной симметрии системы эквивалентна структуре идеального поля. По контуру сферической эквипотенциали V ₀ = 0 круговое движение могут совершать частицы с кинетической энергией W 0 = q ( V ₂ - V ₀ ) = qV 2 ;

соответствующая энергия для движения по контуру эквипотенциали V 2 будет W 2 = ₂ W 0 .

Оказалось, что при назначении на плоские и цилиндрические электроды потенциалов, несколько меньших или равных потенциалам V0 и V2 на обкладках дефлекторов, в эквипотенциальном пространстве могут быть найдены такие позиции точечных источников S1 и S2, при которых для пучков с кинетическими энергиями W0 и W2 осуществляется фокусировка второго порядка по на- правлению. На рис. 2 показаны группы траекторий частиц с кинетическими энергиями W0 и W2, исходящих из источников S1 и S2, и соответствующие им позиции F1 и F2 фокусов второго порядка. Для характеризации дисперсии по энергии на рисунке дополнительно к основным группам показаны группы траекторий с другими кинетическими энергиями: в фокусе F1 на 2 % меньше W0, в фокусе F2 на 1 % меньше W2. Влияние расположения источника на фокусировку характеризует группа траекторий частиц, исходящих из источника S2' с кинетической энергией на 7 % больше W2. Эти траектории образуют фокус второго порядка в симметричном относительно общей оси ОО1 системы положении F2' .

Представляет интерес сопоставление параметров фокусировки рассматриваемой системы и идеального дефлектора. На рис. 3 представлены результаты, отражающие изменения характера фоку- сировки за счет линзового эффекта от провисающего поля.

Для качественного сравнения фокусировки на рис. 3, а, б приведены фрагменты пучков в области кроссовера: а — в случае фокусировки второго порядка в области F2 рис. 2; б — в классическом случае фокусировки первого порядка (семейство С на рис. 1). Пучки 1, 2 и 3 на рис. 3, а соответствуют различным начальным энергиям, отличающимся одна от другой на 0.5 % W2 при угловом растворе пучков, выходящих из источника, равном 5° (пучки 4 и 5 на рис. 3, б также отличаются по энергии на 0.5 %). Видно, что разделение пучков благодаря фокусировке второго порядка существенно выше, чем в идеальном поле. В конкретном случае, показанном на рис. 3, а, предельное энергетическое разрешение оценивается величиной порядка 0.1 %. Аналогичный показатель для фокусировки первого порядка (рис. 3, б) почти в три раза хуже и составляет величину в пределах 0.25–0.3 %. На рис. 3, в приведены функции прилета для пучков, показанных на рис. 3, а, б. В окрестности точки фокуса второго порядка функция

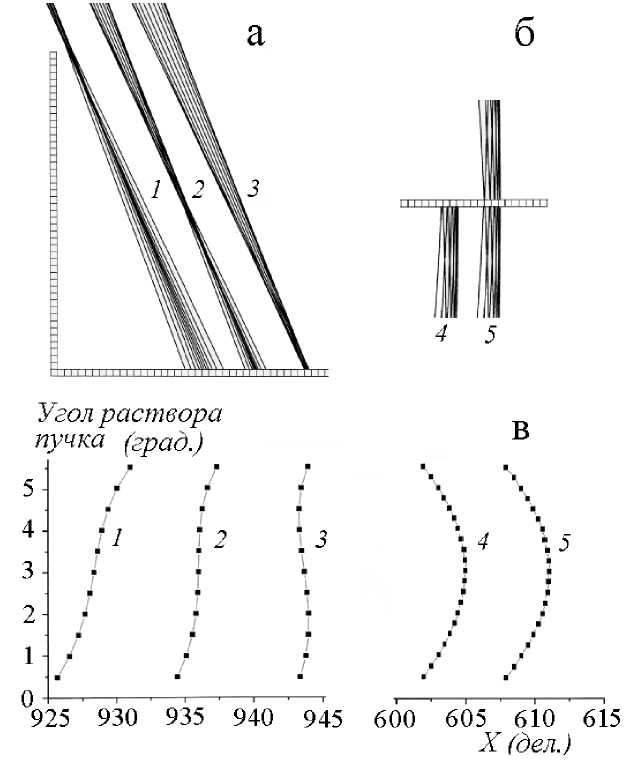
Рис. 3. Качественные характеристики фокусировок второго и первого порядка по направлению в полусферическом дефлекторе с провисающим полем и в идеальном поле:

а — фрагменты пучков 1, 2, 3 с начальными энергиями, отличающимися на 0.5 % в области кроссовера фокусировки второго порядка;

б — фрагменты пучков 4, 5 с начальными энергиями, отличающимися на 0.5 % в области кроссовера фокусировки первого порядка;

в — графики функции прилета пучков с фокусировкой второго (1, 2, 3) и первого (4, 5) порядков

прилета имеет вид функции y = ax + x ³ (параметр a = 0 при перемещении экрана точно в фокус), в то время как для пучков 4 и 5 на рис. 3, б функция прилета имеет вид y = ax ². Для сопоставления функций в одном масштабе графики 4 и 5 сняты для пучков с различиями по энергии 0.5 %. Результаты проведенного анализа иллюстрируют возможность использования линзового эффекта провисающего поля для улучшения характеристик светосилы и энергетического разрешения в реальных системах на основе сферического дефлектора.

КОНФИГУРАЦИИ, ОБЕСПЕЧИВАЮЩИЕ ФОКУСИРОВКУ ВТОРОГО ПОРЯДКА В СЕКТОРНОМ СФЕРИЧЕСКОМ ДЕФЛЕКТОРЕ

Показанная на рис. 2 конфигурация дефлекторов имеет аксиальную симметрию и не может быть использована для анализа энергоугловых распределений пучков по азимутальным направлениям при позициях источников, обеспечивающих фокусировку второго порядка по направлению.

На рис. 4, а показан электростатический энергоанализатор в виде аксиально-симметричного сектора сферического конденсатора с вводом частиц вдоль эквипотенциальных поверхностей поля в плоскости сечения, проходящей через источник и центр сфер. Модель энергоанализатора выполнена по классической схеме и имитирует идеализированную структуру электростатического поля и геометрию расположения элементов. Точечный источник расположен в свободной от поля области на оси аксиальной симметрии системы в позиции S 1 . Электростатическое поле локализовано в пределах секторного угла, равного 90°. Источник создает слабо расходящийся пучок частиц с углом полураствора а / 2. Главная ось пучка составляет с осью аксиальной симметрии системы угол 9 = = 45° и направлена по касательной к средней эквипотенциальной поверхности радиуса r ₀. Ввод и вывод частиц производится через открытый на эквипотенциальное пространство зазор в коническом электроде, служащем для коррекции краевого поля конденсатора [10] и ограничения угловой апертуры пучка величиной порядка 4°.

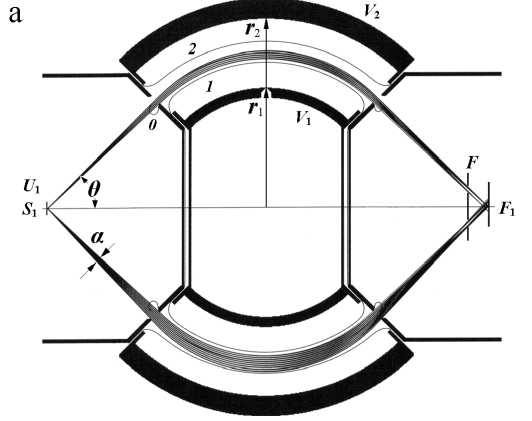
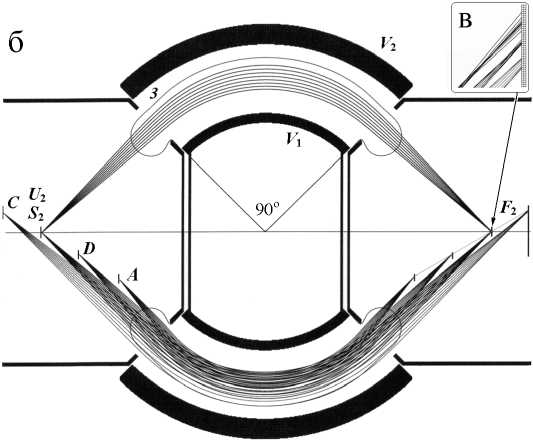
Рис. 4. Энергоанализаторы на основе аксиально-симметричного 90^о сферического конденсатора. r ₂ = 11/9 r ₀, r 1 = 7/9 r ₀, V ₂ = 4/11 U ₀, V 1 = 4/7 U о , где U о — потенциал, соответствующий кинетической энергии частиц W 0 = q U ₀ для движения по окружности радиуса r ₀ в идеальном поле.

а — конфигурация секторного энергоанализатора с фокусировкой по угловым направлениям первого порядка; средняя эквипотенциальная поверхность и корректирующий конический электрод имеют потенциал V 0 = U 1 = 0; S 1 , F 1 — положения источника и фокуса на оси системы; главная ось пучка составляет с осью аксиальной симметрии системы угол 9 = 45°; а — полный угловой раствор пучка (4°); 0, 1, 2 — контуры эквипотенциалей со значениями 0, (4/11) V ₂, (2/9) V ₁ соответственно;

б — конфигурация секторного энергоанализатора с фокусировкой по угловым направлениям второго порядка; корректирующий конический электрод имеет потенциал U ₂ = 8/11 V ₂; 3 — контур эк-випотенциали со значением 7/11 V о ; S ₂, F ₂ — положения источника и фокуса на оси системы; главная ось пучка составляет с осью аксиальной симметрии системы угол 9 = 46°; кинетическая энергия частиц W ₂ = qU ₂ для движения по траекториям с источником и фокусом на общей оси, W ₂ = 11/15 W 0 ; C , D , A — группы траекторий частиц с фокусами второго порядка вне оси системы, соответствующие им кинетические энергии W C = 12/11 W ₂, W D = 10/11 W ₂, W A = 9/11 W ₂.

в — вид фрагментов пучков частиц в области фокуса второго порядка F ₂ с энергиями, отличающимися на 1 % W ₂

Чтобы компенсировать ослабление поля в межэлектродном зазоре на краях сектора и приблизить поле максимально к идеальному (со средней эквипотенциальной поверхностью V 0 центральносимметричного поля), на секторные сферические электроды дополнительно установлены конические вставки под потенциалами обкладок [11]. Межэлектродный зазор равен 4/9 r о , обкладки конденсатора равноудалены от средней эквипотенциальной поверхности, соответственно r ₂ = 11/9 r ₀, r 1 = 7/9 r ₀. При подаче на обкладки конденсатора разнополярных потенциалов — отклоняющего частицы V 2 = 4/11 U ₀ и притягивающего V 1 = 4/7 U ₀, где U 0 — потенциал, соответствующий кинетической энергии частиц W ₀ = qU ₀, — средняя эквипотенциальная поверхность и конический электрод имеют потенциал V 0 = 0, главная траектория, совпадающая с осью пучка, представляет собой часть окружности радиуса r ₀. Идеализированная конфигурация секторного энергоанализатора, пропуская через себя пучок с кинетической энергией W 0 , формирует фокус первого порядка в позиции F 1 на оси системы на равном расстоянии с источником частиц S 1 от общего центра симметрии. Наименьший размер кроссовер пучка в фокусе имеет при углах ввода в поле, обеспечивающих прохождение пучка под эквипотенциалью V 0 = 0. При прохождении пучка над эквипотенциалью V 0 = 0 кроссовер смещается в позицию F , соответствующую минимальному размеру каустики полного пучка с угловым раствором а .

Модификация традиционной схемы энергоанализатора по условиям модели полусферических дефлекторов, показанной на рис. 2, позволяет получить различные конфигурации секторных дефлекторов с фокусировкой по угловым направлениям второго порядка. На рис. 4, б приведен вариант модели дефлектора, практически идентичный классической схеме. Отличия касаются изменений величины апертурного зазора в корректирующем коническом электроде, потенциалов на этом электроде и в пространстве источника и детектора частиц. В приведенной на рисунке модели потенциал в пространстве и на коническом электроде имеет величину U2 = 8/11V2 при потенциалах на обкладках дефлектора, равных потенциалам в классической схеме. Контур эквипотенциали 3 со значением 7/11V2 характеризует провисание поля межэлектродного зазора в эквипотенциальное пространство источника и детектора частиц. S2 и F2 — положения источника и фокуса на оси системы, эквивалентные по координатам традиционной схеме, при этом главная ось пучка составляет с осью аксиальной симметрии системы угол 0 = = 46°, а кинетическая энергия движения частиц W2 = qU2 по симметричным траекториям с источником и фокусом на общей оси составляет вели- чину W2 = 11/15 W0, где W0 соответствует классическому случаю. Для иллюстрации возможностей системы анализировать энергии частиц в полых конических пучках на рис. 4, б показаны дополнительные группы траекторий частиц C, D, A с фокусами второго порядка вне оси системы; соответствующие им кинетические энергии: Wc = 12/11W2, Wd = 10/11W,, Wa = 9/11W2. Дисперсию системы по энергии характеризуют изображения на рис. 3, в фрагментов пучков частиц в области фокуса второго порядка F2 с энергиями, отличающимися на 1 % W2.

На рис. 5 приведены функции прилета пучков, показанных на рис. 4, а, б, позволяющие провести сравнение параметров фокусировки систем. Графики функций построены в одном масштабе для пучков частиц с различиями по энергии 1 %.

Из сопоставления функций следует, что разделение пучков при фокусировке второго порядка выше, чем в идеализированной системе. В показанном на рис. 4, а случае энергетическое разрешение для фокусировки первого порядка составляет величину порядка 0.3 % при угловом растворе пучка а = 4°. Таким же разрешением обладает модифицированный дефлектор при угловом растворе пучка порядка 7-8° (рис. 4, б), при одинаковом угле а = 4° предельное энергетическое разрешение может быть повышено до величины порядка 0.1 %.

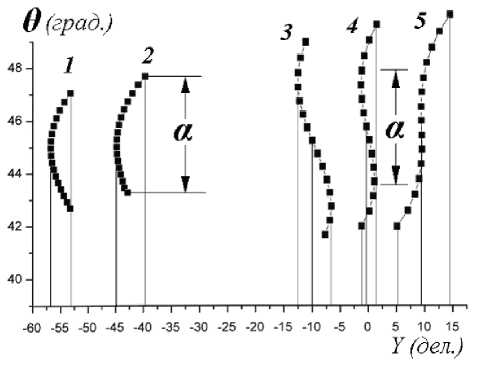
Рис. 5. Графики функции прилета пучков с фокусировкой первого (1, 2) и второго (3, 4, 5) порядков. Графики (1, 2) соответствуют пучкам на схеме рис. 4, а в позиции F с энергиями, отличающимися на 1 % W ₀; графики (3, 4, 5) характеризуют фрагменты пучков на рис. 4, в, полный угловой раствор пучка а = 7°

Таким образом, линзовое действие проникающего в эквипотенциальное пространство поля оказывает положительный эффект на возможности повышения светосилы и разрешения сферического дефлектора. По физической сути модифицированная система представляет собой одиночную электростатическую линзу с изогнутой осью со свойствами разделения в пространстве пучков разных энергий. Ее классический аналог показан на рис. 6, а и представляет собой обычную аксиально-симметричную цилиндрическую одиночную линзу, работающую в режиме ускорения частиц на входе и торможения на выходе. Для иллюстрации аналогичности принципа действия линза размещена в пространстве с общей осью симметрии под внутренним сферическим секторным электродом и имитирует размеры 100° секторного дефлектора (представляющего собой разновидность схемы на рис. 4, б). Цилиндрический электрод линзы имеет внутренний диаметр, равный разности радиусов сфер дефлектора, торцевые дискообразные электроды находятся под одним потенциалом с кони- ческим электродом. При потенциалах на цилиндрическом электроде в пределах от V0 = 0 до V1 линза имеет фокус в позиции F2 для кинетических энергий частиц, равных или больших 0.5 W2 — кинетической энергии движения в дефлекторе по траекториям с источником и фокусом на общей оси.

Геометрия полеобразующих электродов секторного дефлектора может быть существенно упрощена с сохранением практически всех свойств модифицируемой системы. Пример такого исполнения показан на рис. 6, б, где все сферические электроды заменены на комбинацию конических с цилиндрическими.

ЗАКЛЮЧЕНИЕ

Таким образом, в настоящей работе показана возможность получения в системе, основанной на классическом сферическом энергоанализаторе,

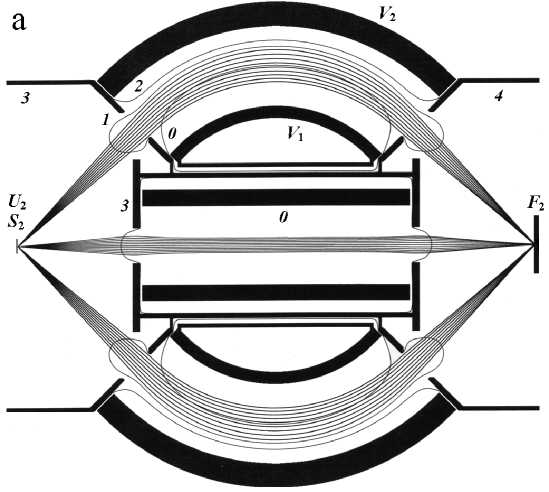
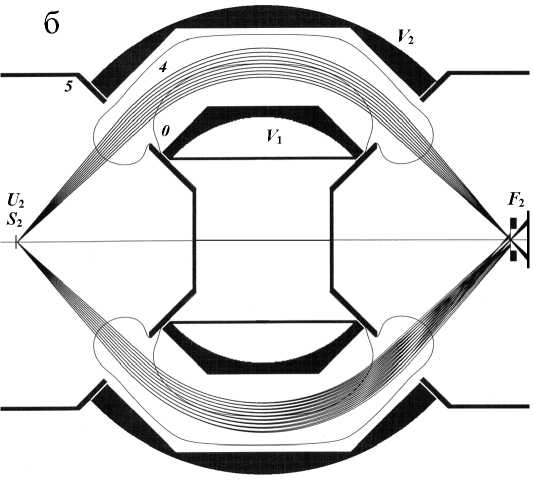
Рис. 6. Энергоанализаторы на основе аксиально-симметричного 100° сферического конденсатора: r 2 = 11/9 r 0 , r 1 = 7/9 r 0 , V 2 = 4/11 U 0 , V 1 = 4/7 U 0 , где U 0 — потенциал, соответствующий кинетической энергии частиц W 0 = = q U 0 для движения по окружности радиуса r 0 в идеальном поле.

а — 100^о сферический дефлектор с аксиально-симметричной цилиндрической одиночной линзой на оси системы; S 2 , F 2 — положения источника и фокуса на оси системы; главная ось пучка составляет с осью аксиальной симметрии системы угол 9 = 44°; конический электрод и элементы 3, 4 под потенциалом U 2 = 6/11V ₂; кинетическая энергия частиц W ₂ = qU ₂ для движения по траекториям с источником и фокусом на общей оси — W 2 = 41/51 W 0 ; 0, 1, 2 — контуры эквипотенциалей со значениями V 0 = 0, (29/55) V 2 , (17/22) V 2 .

б — 100^о секторный дефлектор с упрощенной геометрией полеобразующих электродов; 0, 4 — контуры экви-потенциалей со значениями V 0 = 0, (9/11) V 2 ; конический электрод 3 под потенциалом U 2 = 10/11 V 2 ; S 2 , F 2 — положения источника и фокуса на оси системы; главная ось пучка составляет с осью аксиальной симметрии системы угол θ = 46^о

режимов и конфигураций, обеспечивающих фокусировку второго порядка по угловым направлениям. Найденные конфигурации обладают свойствами одиночной линзы с изогнутой осью и могут быть легко преобразованы в новые оптические элементы с высоким качеством пространственной фокусировки по угловым направлениям в сочетании с большой энергетической дисперсией. Автор выражает искреннюю признательность М.И. Явору за полезные замечания, дискуссии и предоставление возможности использования программ моделирования электронно-оптических систем [12].