Пространственная модель генетического кода в виде полуправильного многогранника "усеченный октаэдр"
Автор: Корчмарюк Ян Илларионович, Коваленко Александр Владимирович
Журнал: Природные системы и ресурсы @ns-jvolsu
Рубрика: Биология и биотехнология
Статья в выпуске: 4 (18), 2016 года.
Бесплатный доступ
В настоящей работе, относящейся к области биоинформатики, математико-статистическим методом факторного анализа анализируются все 4! = 24 перестановки чисел «1, 2, 3, 4» как 4 фактора. В результате численного анализа получены 4 факторные координаты (x, y, z). Минимальные евклидовы расстояния между всеми 24 вершинами образуют ребра фигуры «усеченный октаэдр». Каждой вершине усеченного октаэдра сопоставлен триплет - кодон генетического кода и соответствующая ему аминокислота. Построены графики проекций фигуры «усеченный октаэдр» и изометрическое (трехмерное) ее изображение. Проанализированы обнаруженные закономерности в физических и химических свойствах аминокислот, распределенных по вершинам построенной фигуры. Произведена интерпретация трех факторных осей координат.
Усеченный октаэдр, факторный анализ, генетический код, перестановки, биоинформатика
Короткий адрес: https://sciup.org/149131404
IDR: 149131404 | УДК: 577.21 | DOI: 10.15688/jvolsu11.2016.4.3
The spatial model of genetic code in the form of a semiregular polyhedron "truncated octahedron"
This work applies to the field of bioinformatics and analyzes all 4! = 24 permutations of numbers 1, 2, 3, 4 as 4 factors by means of factor analysis. Computational analysis helped us to get 4 factor coordinates - x, y, z. Minimum Euclidean distances between all 24 vertices create edges of truncated octahedron. Every vertex of truncated octahedron matches with a triplet (it is the genetic code's codon) and appropriate amino acid. We have created the graph of truncated octahedron's projections and its isometric (three-dimensional) image. We have also analyzed detected sequences in physical and chemical characteristics of amines which are located in vertices of our figure. We have interpreted three factor axis of coordinate system.
Текст научной статьи Пространственная модель генетического кода в виде полуправильного многогранника "усеченный октаэдр"
DOI:
Методы математического анализа давно и широко используются для изучения генетического кода [4; 12; 20]. Наиболее популярен кластерный анализ [13; 18], а также методы комбинаторики [7] с широкими возможностями перестановок [6; 8; 10; 11]. Но с исходным представлением генетического кода на уровне кибернетики до сих пор существуют различные вариации. Мы обратили внимание, что пространственные модели лучше опи-
сывают взаимосвязь элементов в системе, а усеченный октаэдр встречается только в поле изучения скаффолдов [17]. Хотя он может быть основой для связи нескольких десятков элементов друг с другом, его до настоящего момента не рассматривали как каркас для генетического кода. В связи с вышесказанным цель нашей работы – построить пространственную модель генетического кода на основе усеченного октаэдра.
Материалы и методы
Исходными данными были взяты 4! = 24 всевозможные перестановки натуральных целых положительных чисел {1, 2, 3, 4}[5; 9]. В качестве математико-статистического метода обработки данных был взят классический метод факторного анализа в программном комплексе «SPSS» с использованием методов главных компонент, Варимакс и нормализации Кайзера [1; 3; 16].
С целью построения трехмерной фигуры по данным трех факторных координат были построены евклидовы расстояния ( Rij = Ö(( xi – xj )2 + ( yi – yj )2 + ( zi – zj )2) между всеми { i , j } 24 вершинами усеченного октаэдра. Все расстояния были нормированы на наименьшее из расстояний. Из всех нормированных расстояний была вычтена 1 (единица), для того, чтобы расстояние у вершин было равно 0 (нулю). Затем были выбраны все пары вершин, между которыми было нормированное 1 (единичное) расстояние, которое было взято за ребро усеченного октаэдра.
Для графического представления итоговых данных по усеченному октаэдру использовались графики трех проекций факторных осей.
Для корректности построенной аналогии 4 нуклеотида ДНК/РНК (CUAG) были упорядочены по возрастанию их молекулярной массы [2; 14; 15; 19] и поставлены в соответствие меткам вершин усеченного октаэдра (1234), следующим образом: 1 = С, 2 = U или Т, 3 = А, 4 = G.
Результаты
Построенная модель «усеченного октаэдра» обладает достаточной мерой общности, чтобы интерпретировать ее в различных теоретических приложениях. В настоящей статье авторами данная модель интерпретирована как трехмерный аналог известной кодовой таблицы 4 нуклеотидов и кодируемых ими 20 аминокислот. Из кодовой таблицы ДНК были выбраны все аминокислоты, которые соответствовали кодонам с неповторяющимися тройками нуклеотидов. Эти аминокислоты были приписаны соответствующим вершинам усеченного октаэдра по первым трем меткам четырехзначного кода их вершин. Старт-коды и стоп-коды были обозначены везде как «STOP» (рис. 1–4). Данные приведены в таблице.
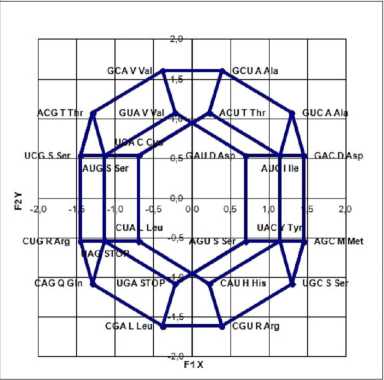
Рис. 1. Генетический код в виде усеченного октаэдра, проекция XY
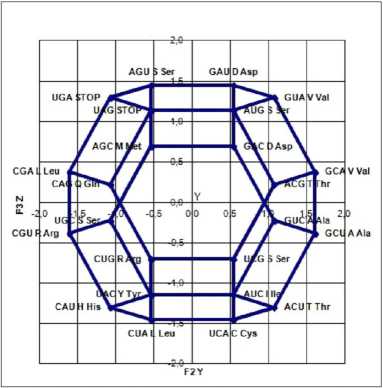
Рис. 2. Генетический код в виде усеченного октаэдра, проекция YZ
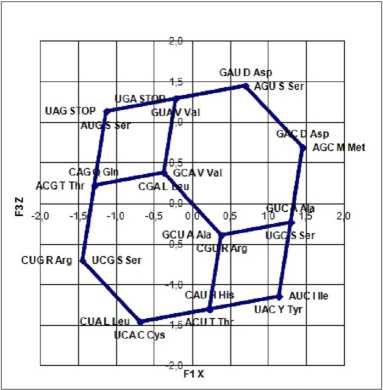
Рис. 3. Генетический код в виде усеченного октаэдра, проекция XZ
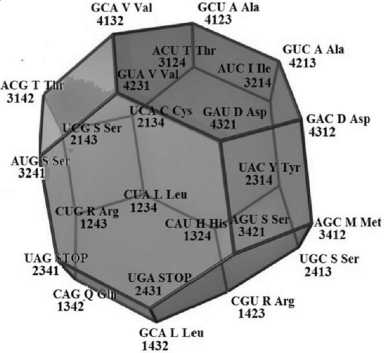
Рис. 4. Генетический код в виде усеченного октаэдра, проекция 3D
Обсуждение
Поскольку все вершины усеченного октаэдра лежат на поверхности описанной около него сферы, а все комбинации перестановок, начинающихся на 1, 2, 3 или 4, – лежат в одной плоскости сечения, то эти перестановки можно интерпретировать как «параллели глобуса», а связывающие их ребра – как «меридианы глобуса». При этом полученная трехмерная модель генетического кода обладает высокой симметрией, почти сферической, и выделяет подгруппу высокоэнтропийных (невырожденных) кодонов и их аминокислот из общей группы генетического кода, а также подгруппу «близколежащие и даль-нележащие коды и аминокислоты». Те, что в вершинах 6-угольников и 4-угольников.
Так как все расстояния в этой модели укладываются на логарифм (значения F1–F3 таблицы), то появляется возможность анализировать корреляции этих 10 типовых расстояний с параметрами кодонов и аминокислот.
Заключение
В силу большой общности построенной модели ее можно использовать в любых кодовых системах, которые имеют базовый алфавит в 24 (или менее) знаков. Например, в математической лингвистике, для букв и звуков алфавитов различных языков мира. Также построенную модель можно использовать в области искусственного интеллекта, если каждую вершину считать «формальным нейроном» в рамках персептронной парадигмы Розенблатта – Мак-Каллоха – Питса, а весовые коэффициенты межнейронных связей приписывать ребрам усеченного октаэдра.
Соотнесение генетического кода с усеченным октаэдром
|
Генетический код CUAG |
Метка перестановок |
Факторные оси |
|||||
|
F1 = X |
F2 = Y |
F3 = Z |
|||||
|
C |
U |
A |
L Leu |
1234 |
-0,69324 |
-0,53619 |
-1,45152 |
|
C |
U |
G |
R Arg |
1243 |
-1,45152 |
-0,53619 |
-0,69324 |
|
C |
A |
G |
Q Gln |
1342 |
-1,29448 |
-1,07238 |
0,22210 |
|
C |
G |
A |
L Leu |
1432 |
-0,37914 |
-1,60857 |
0,37914 |
|
C |
G |
U |
R Arg |
1423 |
0,37914 |
-1,60857 |
-0,37914 |
|
C |
A |
U |
H His |
1324 |
0,22210 |
-1,07238 |
-1,29448 |
|
U |
C |
A |
C Cys |
2134 |
-0,69324 |
0,53619 |
-1,45152 |
|
U |
C |
G |
S Ser |
2143 |
-1,45152 |
0,53619 |
-0,69324 |
|
U |
A |
G |
STOP |
2341 |
-1,13743 |
-0,53619 |
1,13743 |
|
U |
G |
A |
STOP |
2431 |
-0,22210 |
-1,07238 |
1,29448 |
|
U |
G |
C |
S Ser |
2413 |
1,29448 |
-1,07238 |
-0,22210 |
|
U |
A |
C |
Y Tyr |
2314 |
1,13743 |
-0,53619 |
-1,13743 |
|
A |
C |
U |
T Thr |
3124 |
0,22210 |
1,07238 |
-1,29448 |
|
A |
C |
G |
T Thr |
3142 |
-1,29448 |
1,07238 |
0,22210 |
|
A |
U |
G |
S Ser |
3241 |
-1,13743 |
0,53619 |
1,13743 |
|
A |
G |
U |
S Ser |
3421 |
0,69324 |
-0,53619 |
1,45152 |
|
A |
G |
C |
M Met |
3412 |
1,45152 |
-0,53619 |
0,69324 |
|
A |
U |
C |
I Ile |
3214 |
1,13743 |
0,53619 |
-1,13743 |
|
G |
C |
U |
A Ala |
4123 |
0,37914 |
1,60857 |
-0,37914 |
|
G |
C |
A |
V Val |
4132 |
-0,37914 |
1,60857 |
0,37914 |
|
G |
U |
A |
V Val |
4231 |
-0,22210 |
1,07238 |
1,29448 |
|
G |
A |
U |
D Asp |
4321 |
0,69324 |
0,53619 |
1,45152 |
|
G |
A |
C |
D Asp |
4312 |
1,45152 |
0,53619 |
0,69324 |
|
G |
U |
C |
A Ala |
4213 |
1,29448 |
1,07238 |
-0,22210 |
Список литературы Пространственная модель генетического кода в виде полуправильного многогранника "усеченный октаэдр"
- Козлов, Н. Математический анализ генетических кодов/Н. Козлов//Математическая биология и биоинформатика. -2006. -Т. 1, № 1. -С. 70-96.
- Козлов, Н. Один способ хранения генетической информации/Н. Козлов//Математическое моделирование. -2002. -Т. 14, № 8. -С. 72-78.
- Козлов, Н. О расчете генетического кода/Н. Козлов//Математическое моделирование. -2011. -Т. 23, № 6. -С. 3-17.
- Козлов, Н. Тайны генетического кода: взгляд математика/Н. Козлов//Математическое моделирование. -2015. -Т. 27, № 4. -С. 64-80.
- Корчмарюк, Я. Усеченный октаэдр как результат факторного анализа полной группы перестановок из чисел {1, 2, 3, 4}/Я. Корчмарюк//Сборник ВорГТУ «Современные проблемы информатизации в технике и технологиях». -2002. -№ 7. -С. 58-60.
