Пространственная модель подвески транспортного средства со стабилизатором поперечной устойчивости

поведение элементов подвески и транспортного средства в целом.

Одним из путей решения задач исследования динамики ходовых систем, широко применяемых в мировой практике, является использование математических моделей, описывающие динамическое поведение транспортного средства как многомассовой механической системы с сосредоточенными массами, имеющими вязкоупругие и кинематические связи [1, 2]. Перемещение масс эквивалентных колебательных систем определяются координатами, выбранными в соответствии с характеристикой взаимодействия отдельных элементов конструкции и видом упругих деформаций между условно недеформи-руемыми массами. На рис. 1 приводится пример эквивалентной расчетной пространственной модели легкового автомобиля с независимой подвеской как пятимассовой механической системы с упругими и демпфирующими связями.

Центр системы координат совпадает с центром масс кузова. Инерционные параметры системы характеризуются массой ( m 1 ) и моментами инерции ( J х , J y ) кузова, а так же массами непод-рессоренных частей передней ( m 2 , m 4 ) и задней ( m 3 , m 5 ). Упругие и гасящие элементы подвески представлены в виде пружин с коэффициентами жесткости ( K 2 -K 5 ) и амортизаторов с коэффициентами демпфирования ( С 2 -С 5 ). Вязкоупругие свойства шин заданы коэффициентами жесткости ( K 6 -K 9 ) и коэффициентами демпфирования ( С 6 -С 9 ). В качестве обобщенных координат принимаются вертикальные перемещения элементов ( z i ) и углы поворота кузова относительно продольной и поперечной осей ( ϕ x , ϕ y ).

Рассматриваемую схему необходимо дополнить соотношениями, учитывающими влияние стабилизаторов поперечной устойчивости. Рассмотрим упрощенную модель стабилизатора поперечной устойчивости, которая представляет собой П-образную штангу. Центральная часть шарнирно закреплена в опорах и выполняет роль торсиона (рис. 2).

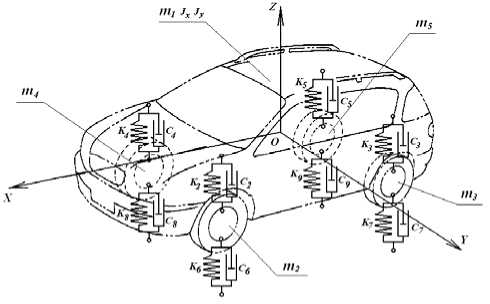
Рис. 1. Пространственная модель транспортного средства с упругой подвеской

Концы штанги выполняют роль рычагов с длиною плеча B . Под воздействием сил P 1 и P 2 , приложенным рычагам торсиона, происходит их перемещение от начального положения на величины h 1 и h 2 . Концы торсиона соответственно закручиваются на различные углы ( α 1 , α 2 ). При этом в самом торсионе возникает момент кручения, зависящий от разностей углов закручивания и коэффициента угловой жесткости ( K φ ):

Mкр = (Pi - P2)B = (ai - a2)Kp . (1)

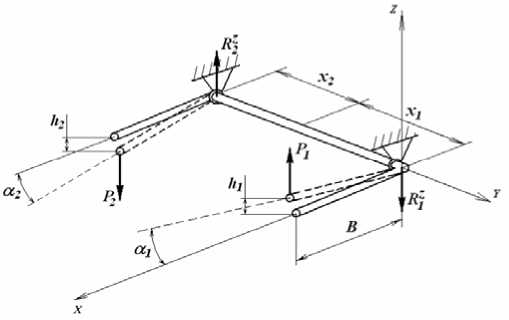
Рис. 2. Расчетная пространственная схема стабилизатора поперечной устойчивости

Коэффициент угловой жесткости торсиона круглого сечения вычисляется в зависимости от модуля сдвига G , диаметра d и длины торсиона L по формуле:

K _p = G n d ⁴/32 L . (2)

Принимая допущение, что углы α 1 и α 2 малы, зависимости для вертикальных перемещений выразятся в виде:

а1 = h11 B , a2 = h21 B. (3)

С учетом соотношений (1, 3) можно записать следующее соотношение:

Px - P2 = (h - h2)K IB2. (4)

Из этого выражения можно вывести приведенный коэффициент жесткости стабилизатора поперечной устойчивости:

к ст = K I B 2 .           (5)

Кроме того, при воздействии сил P 1 и P 2 в опорах образуются силы реакции, вертикальные составляющие которых R^z 1 и R^z 2 . Учитывая, что опоры связаны с корпусом транспортного средства, реактивные усилия образуют момент относительно продольной оси.

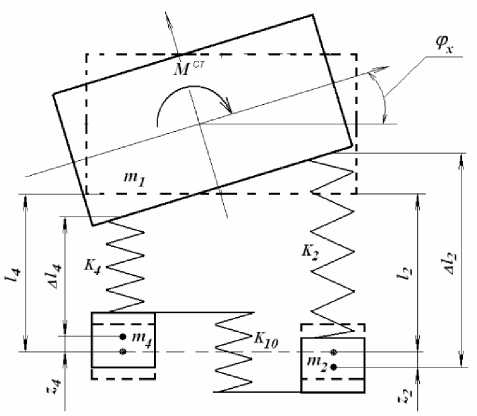
Рис. 3. Эквивалентная схема стабилизатора поперечной устойчивости

На рис. 3 приведена эквивалентная расчетная схема передней подвески со стабилизатором поперечной устойчивости. Жесткостная характеристика стабилизатора задана приведенным коэффициентом жесткости K 10 . Начальные положения неподрессоренных масс ( m₂ , m₄ ) относительно корпуса ( m 1 ) – это расстояния l 2 и l 4 . Изменение взаимного положения элементов рассматриваемой подсистемы зависит от вертикальных перемещений ( z 1 , z 2 , z 4 ) и угловых перемещений кузова продольной и поперечной осей (p x , p y ), а так же от координат расположения элементов относительно вертикальной оси ( x i и y i ).

С учетом соотношений (3)-(4) усилие, возникающее при деформации пружины K₁₀ запишется как

A P 24 = К ,о (А 1 2 -A 1 4 ) =

= К 1о ( 1 2 + z 2 - z 1 - х 2 P y - У 2 P x - 1 4 - z 4 + Z 1 + X 4 P y + У 4 P x ) или

^ P 24 = ^K 10 ( z 2 - z 4 + ( х 4 - х 2 ) Ф у + ⁽ У 4 - У 2 ) Ф х ) ^.

Выражение для стабилизирующего момента запишется как

^M 10 = ^K 10 y 2 ⁽ z 4 - z 2 ^{+ (} х 2 - х 4 ^{) ф} у ^{+ (} y 2 - y 4 ) ^ф x ) ^.

На рис. 4 показана эквивалентная расчетная схема транспортного средства с упругой подвеской и стабилизаторами поперечной устойчивости. С учетом выражений (6) и (7) динамическое поведение данной модели описывается системой дифференциальных уравнений:

• «1 z - zi £ Ki - фу £ Kx - Фх £ Kx.+^L Kz -=1                   ,=1                       i=1i

  5555 ....

• - ^z 1 £ C i -ф у £ C - X i - Ф х £ c - y - + £ C - Z i = 0;

i =1                   i =1                       i =1

« i z i - z i ^{( K}i ^{+ K}i + 4 ) ⁺ Kz 1 ⁺ Ф у^Ki^Xi ⁺ Ф х^У . -

• - z . ( C i + C i + 4 ) + C 1 Z 1 +

  у C , x , + Ф x C i y i =

= f + 4 K i + 4 + f . + . C , + 4 , ii = 2..5;

« 6 z 6 — z 6 K 1 ⁺ K 1^z 6 ⁺ Ф у^К 1 ^X 6 ⁺ Ф х^К 1 У 1 —

• -    z 6 C ₁ + C ₁ z 6 + ф _у C_ix₁ + ф _х C ₁ у ₁ = 0;

Jx Ф>х - z 1 '£ K ,У i - Фу ^£ K ,x i У i - Фх ]£ K ,У -2 + £ K ,z ,У i -=1                     i=1                         i=1

• -    = 1 £ C , у , - Ф у £ C - х . у , - Ф х £ C . y- ; + £ C , z , у , = 0;

i =1                     i =1                         i =1

J у Фу-А K.x. - Фх £ K-x^ - фу £ Kixi +£ Kizixi -i=1                    i=1                         i=1

• - z 1 £ C , x , - Ф х £ C - X_iy_i - ф у £ C i x' + £ Cz i x. = 0.

i=1                    i =1                        i =1

Для решения системы дифференциальных уравнений используется метод временных конечных элементов [4], на основе которого разработан программный комплекс SUSPEND [6] В качестве примера рассмотрена модель транспортного средства, приведенная в работах [5, 6] Исходная модель модифицирована с учетом пространственного расположения элементов подвески Внешнее воздействие задается в виде вертикальных смещений передних и задних шин, которые зависят от профиля дороги и скорости движения транспортного средства v , характер которого аналогичен описанному в работе [6]

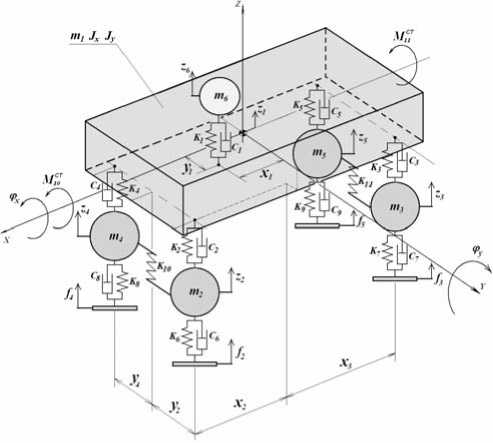
Рис. 4. Эквивалентная расчетная схема транспортного средства с упругой подвеской и стабилизаторами поперечной устойчивости

Для исследования поперечных угловых колебаний рассмотрено несимметричное внешнее кинематическое воздействие, имитирующее въезд в пологую яму колесами левой стороны транспортного средства С использованием разработанного программного проведены динамические расчеты с целью исследования влияния стабилизаторов поперечной устойчивости на динамическое поведение транспортного средства Значения приведенных коэффициентов жесткости стабилизаторов K 10 = K 11 =10000 Н/м На рис 5 и 6 приведены графики угловых колебаний корпуса относительно продольной оси и поперечной оси для исходной конструкции, конструкции с одним передним стабилизатором и конструкции с двумя стабилизаторами Кроме того, на рис 7 показаны графики динамических откликов на водительском кресле

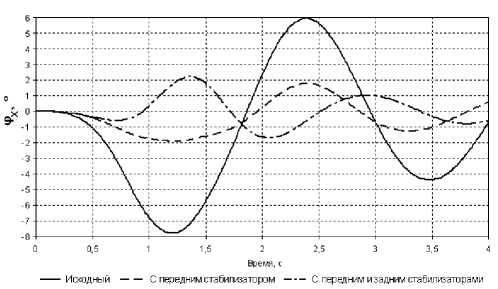
Рис. 5. Графики угловых перемещений корпуса относительно продольной оси для различных конструкций

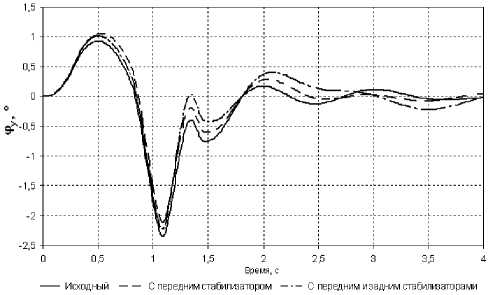
Рис. 6. Графики угловых перемещений корпуса относительно поперечной оси для различных конструкций

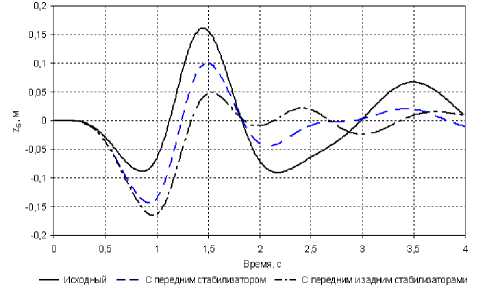
Рис. 7. Вертикальные перемещения кресла водителя

Выводы:

• -    применение стабилизаторов поперечной устойчивости мало влияет на угловые колебания корпуса относительно поперечной оси, при этом существенно снижается уровень колебаний относительно продольной оси;

• -    для рассматриваемой конструкции существенное снижение амплитуды угловых колебаний относительно продольной оси достигается введением одного переднего стабилизатора поперечной

устойчивости, дополнительное введение заднего стабилизатора несколько изменяет картину поперечных угловых колебаний, однако амплитуда колебаний остается прежней;

• -    применение стабилизаторов снижает амплитуду вертикальных перемещений рабочего места водителя и уровень вертикальных ускорений, что положительно сказывается на комфортабельности, причем существенное снижение так же достигается путем применения одного переднего стабилизатора.

Приведенные в работе соотношения можно модифицировать для описания динамического поведения моделей транспортных средств с подвеской иных конструкций, как зависимых, так и независимых.