Пространственная селективность четырёхволнового преобразователя излучения в прозрачной двухкомпонентной среде в схеме с попутными волнами накачки

Для получения волны с обращённым волновым фронтом (ОВФ) при четырёхволновом взаимодействии используются две схемы: схема со встречными и схема с попутными волнами накачки [1, 2]. Выбор той или другой схемы зависит от решаемой задачи, требований, предъявляемых к волне с ОВФ. При четырёхволновом взаимодействии в схеме со встречными волнами накачки происходит полное обращение волнового фронта падающей (сигнальной) волны. Волна с обращённым волновым фронтом (объектная волна) распространяется навстречу сигнальной волне, и при её прохождении вновь через ту же оптически-неоднородную среду, через которую проходила сигнальная волна, компенсируются внесённые в сигнальную волну фазовые искажения [3].

В схеме с попутными волнами накачки происходит обращение лишь поперечной составляющей волнового вектора падающей волны. Волна с ОВФ распространяется в направлении сигнальной волны. Это может оказаться предпочтительным, например, при компенсации фазовых искажений, возникающих при распространении сигнальной волны через одну оптически-неоднородную среду, а волны с ОВФ через другую оп-тически-неоднородную среду, параметры которой совпадают или близки к параметрам первой среды [4].

Как схема четырёхволнового взаимодействия со встречными, так и схема с попутными волнами накачки применяются для обработки и анализа изображений, в квантовой криптографии, для сверхскоростной оптической обработки сигналов и т.д. [5–7].

До настоящего времени анализ качества ОВФ проводился для четырёхволновых преобразователей излучения с попутными волнами накачки в средах с керровской, резонансной, тепловой нелинейностями [8–10]. В последние годы активно обсуждается возможность использования для реализации четырёхволновых взаимодействий сред, содержащих частицы микро- и наноразмеров (коллоидные растворы, суспензии и т.д. [11–16]). При использовании в качестве нелинейных сред жидкостей, содержащих наночастицы, существенное влияние на пространственную структуру волны с ОВФ могут оказывать такие физические процессы, как электрострикция и эффект Дюфура [17–19].

В настоящей работе анализируется пространственная селективность четырёхволнового преобразователя излучения с попутными волнами накачки в прозрачной жидкости, заполненной наночастицами, плотность которых равна плотности жидкости.

1.    Модель четырёхволнового взаимодействия

Рассмотрим типичную схему вырожденного четырёхволнового взаимодействия ω + ω – ω = ω с попутными волнами накачки в плоском слое толщиной ℓ (рис. 1).

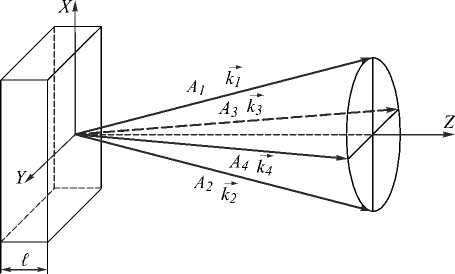
Рис. 1. Схема четырёхволнового взаимодействия с попутными волнами накачки

В среде распространяются попутно две плоские волны накачки с комплексными амплитудами A1,2 (Г) = A^ (z) exp (-ik12r) (k12 (к1,2, k12z) - волновые векторы волн накачки, z – продольная составляющая радиус-вектора r) и сигнальная волна с комплексной амплитудой A3. Будем считать, что волновые вектора волн накачки лежат в плоскости XZ (плоскости волн накачки). Интерференция волн накачки и сигнальной волны приводит к изменению в пространстве интенсивности излучения и, вследствие электрострикции, к возникновению потока концентрации наночастиц. Из-за эффекта Дюфура поток концентрации изменяет температуру (5 T), а значит, и показатель преломления среды 5n = (dn/dT)5T. В результате дифракции волн накачки на решётках показателя преломления генерируется объектная волна с комплексной амплитудой A4.

Исходное уравнение Гельмгольца, описывающее четырёхволновое взаимодействие излучения в прозрачной нелинейной среде, имеет вид [17, 18]

V ² + к ² + —— 8 T |( A + AЛ = 0, n 0 d T J^V ’

где A = ^ A . , к = to n 0 / c , и - циклическая частота, n 0 - j =1

среднее значение показателя преломления, c - скорость света.

Уравнение (1) дополняется системой материальных уравнений для изменений концентрации (5 С ) и температуры [11, 19]

д8 С/ д t = D ₂₂ V ² 8 С + yV ² 1 ,                     (2)

c p v ^j T = D 11 V 2 8 T + D ₁₂ V ² 8 C .

Здесь D 11 , D 22 , D 12 и у - коэффициенты теплопроводности, диффузии, Дюфура и электрострикции соответственно, c p - удельная теплоёмкость вещества, v - плотность вещества, I=AA * - интенсивность излучения.

• 2.    Четырёхволновое взаимодействие с учётом температурных решёток, возникающих при интерференции волн накачки и сигнальной волны

Для установившегося (стационарного) режима (д5С/дt = 0, д5T/дt = 0) из системы материальных уравнений (2) - (3) получим уравнение, связывающее изменение температуры с интенсивностью взаимодействующих волн

V ² 8 T    ^Y D ' ² V ² 1 .                                (4)

D 11 D 22

В приближении заданного поля по волнам накачки (|A 1,2|>>|Aз,4|), при малом коэффициенте преобразования (|A4|<<|Aз|) интенсивность излучения, распространяющегося в нелинейной среде, можно записать следующим образом i = 10+A a;+a; a3+A a;+a ; a3 ,             (5)

где 1 0 1 1 + 1 2 , 1 1,2 = A 1,2 A*₂ .

Тогда изменение температуры можно представить в виде суммы быстро (5 T ₃₁, 5 T ₃₂) и медленно (5 T ) ) меняющихся в зависимости от координат составляющих

8 T ( r ) = 8 T ( z ) + 8 T 31 ( r ) + 8 T 3; ( r ) + +8 T 32 ( r ) + 8 T^ ( r ) .

Сигнальную и объектную волны разложим по плоским волнам, а быстро меняющиеся составляющие изменения температуры - по гармоническим решёткам

^

^Aj ( r ) = J ^Aj ( * . z ) ^eX P ( - i ^ P ^- ik jz z ) ^ j ,        ⁽⁷⁾

-^

M

• ^{8    T} 31,2 ⁽ r ) = J ^{8 T} 31,2 ( ^K T 1,2 , z ) ^eX P ( ^— i ^K T 1,2 ^P ) ^{d K} T 1,2^{. (8)} -^

Здесь A - пространственный спектр -й волны, 8T31,2 - пространственные спектры температурных решёток, к..(к., к.y) и к. - поперечная и продольная составляющие волнового вектора kj, j=3,4, |kj| = к, кT 1,2 (кTi,2x, кT 1>2у) - волновые векторы температурных решёток, р (x, у) - поперечная составляющая ра- диус-вектора.

Как показано в работах [9, 10], при выполнении граничного условия A ₄ ( K ₄, z = 0 ) = 0 и записи в нелинейной среде только температурных решёток пространственный спектр объектной волны на задней грани нелинейного слоя связан со спектрами температурных решёток следующим выражением

• -Vfr.             k d n -

• A^(к4, z = l ) = 1   лтА20 X

n ₀ d 1

l xJ 8T31 (кT1, z) exp [-i (к2z - к4z) z] dz -             (9)

- i

i

^A 10 J ^{8 T} 32 ( ^к T 2 , z ) ^eX P ^[- i ( ^к 1 z ^{- к} 4 z ) z J dz .

к d n n ₀ d T

Здесь A ^ ( к ₄, z ) = A₄ ( к ₄, z ) exp [ P ( z ) ] ,

, , к d n z _       -        -

P ( z ) = l— TfJ 8 T0 ( z1 ) dz 1, "A1,20 = "A1,2( z = 0). Выра- n 0 d T 0

жение (9) записано при квазиколлинеарном распространении взаимодействующих волн, при условии к ₄ = к _T 1 + к ₂ = к _{T 2} + к 1 .

Выражение для пространственного спектра объектной волны дополняется системой дифференциальных уравнений, полученных из материального уравнения (4), описывающих изменение пространственных спектров температурных решёток по толщине нелинейного слоя

( d ²    о Ъ ~ /р

I J 2 ^{- к} T 1,2 I ^{8 T}31,2 ^(к T 1,2 , ^z ) =

X dz        /

D

= ^-Y yH2- ^A 1,20 ^A 30 ( ^к 3 ) ^{x                       (10)}

^D 11 ^D 22

X [кT1,2 + ( к1,2z - к3z )2 ] eXP [-i ( к1,2z - к3z ) z] , где A30 (к3 ) = A30 (к3, z = 0) , кT 1,2 = к1,2 - к3 .

При неизменности температуры на гранях нелинейного слоя ( 8 T ₃₁ , ₂ ( к _T 1, ₂, z = 0 ) = 8 T ₃₁ , ₂ ( к _T 1, ₂, z = I ) = 0 ) решение уравнений (10) есть

^{8 T} 31,2 (^к T 1,2 , z )   „ „ ^A 1,20 ^A 30 ^(к 3 ^)X

^D 11 ^D 22

x ( ( sh к _T 1, ₂ l ) { exp [- i ( к 1, _{2 z} - к 3 _z ) l ] sh к _T 1, ₂ z -     (11)

• ^- sh ^к T 1,2 ( ^{z - l} ) } ^{- eX} P ^{[- 1} ( ^к 1,2 z ^{- к} 3 z ) ^z ] ) .

Подставив (11) в (9) и проинтегрировав по координате z , получим пространственный спектр объектной волны на задней грани нелинейной среды

A 4 ( К 4 , z = I ) = A 41 ( К 4 , z = I ) + Д ^ ( к 4 , z = I ) . (12)

Здесь

A41,2 ( К4, z = 1) = -i-k^Dib-^nX n0D11D22 dT

~ ~ ~                          —1

XA10A20 A30 (К3 ) I ( 2shКT 1,21) X xMexpl — i (k1,2 z — k3 z) I I — exp (—к T 1,21 )}x

X

exp { [^К T 1,2 ^— i ( ^k 2,1 z ^{— k} 4 z ) ] ^l } ^{— 1}

^К T 1,2 ^— i ( ^k 2,1 z ^{— k} 4 z )

+

+ { exp [— i ( k 1 _{2 z} — k _{3 z} ) I ] — exp ( к T 1 ₂ 1 ) } x

X

exP { ^{— [К} T 1,2 ⁺ i ( ^k 2,1 z ^{— k} 4 z ) ] ^l } ^{— 1}

^К T 1,2 ⁺ i ( ^k 2,1 z ^{— k} 4 z )

—

• —i A 1 [exp (— iM) — 1]],

A = ( k 1 + k ₂ — k ₃ — k ₄) _z - проекция волновой расстройки на ось Z , к T 1, ₂ = | К T 1, ₂1. В параксиальном приближении А = ( К 1 —К ₄)( К ₂ —К ₄)/ k .

Пространственный спектр объектной волны является суммой пространственных спектров двух волн, одна из которых возникает при дифракции первой волны накачки на температурной решётке 8 T ₃₂, другая – при дифракции второй волны накачки на температурной решётке 8 T ₃₁. Если одна из волн накачки, например A 2 , некогерентна первой волне накачки и сигнальной волне, то в нелинейной среде записывается одна температурная решётка 8 T ₃₁ и пространственный спектр объектной волны определяется пространственным спектром волны A ₄₁ .

В этом и последующих параграфах будем считать, что сигнальной волной является волна от точечного источника, расположенного на передней грани нелинейного слоя ( A ₃₀( К ₃) = 1).

На рис . 2 приведены характерные модули пространственных спектров объектной волны при наличии одной (рис. 2 а ) и двух (рис . 2 б ) температурных решёток при условии, что волны накачки падают на нелинейную среду под одинаковыми углами ( К 1 = — К ₂). Зависимость проекции волновой расстройки на ось Z от поперечных составляющих волновых векторов взаимодействующих волн (условие фазового синхронизма) определяет общий вид модуля пространственного спектра объектной волны [8], а наличие электрострикции и эффекта Дюфура – возникновение в модуле спектра провалов , положения которых соответствуют направлениям распространения волн накачки.

При записи одной температурной решётки 8T31 и учёте только условия фазового синхронизма в плос- кости волн накачки ((К4 К2) = К4 К2) в пространственном спектре объектной волны наблюдаются два максимума, положения которых задаются пространственными частотами волн накачки К1 2 = | К 1 21. Как следует из (11), учёт, наряду с условием фазового синхронизма, явления электрострикции и эффекта Дюфура приводит к отсутствию температурной решётки при Кt 1^0, к возникновению в модуле пространственного спектра объектной волны на пространственной частоте второй волны накачки вместо максимума провала (рис. 3а). При фиксированном угле падения первой волны накачки поворот второй волны накачки смещает положение провала в пространственном спектре на величину поворота.

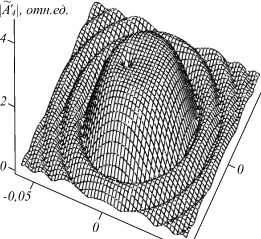
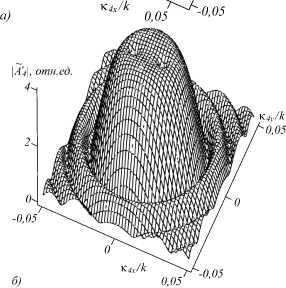
Рис. 2. Пространственные спектры объектной волны с учётом одной (а) и двух (б) температурных решёток

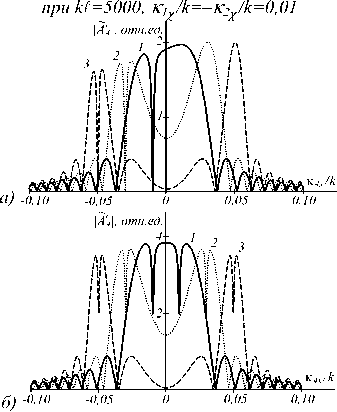
Рис. 3. Пространственные спектры объектной волны в плоскости волн накачки с учётом одной (а) и двух (б) температурных решёток при k I =5000, K i _z /k^- K_2z /k=0,01 (1), 0,03 (2), 0,05 (3)

Направления распространения волн накачки не влияют на модуль пространственного спектра объектной волны в области провала.

При записи двух температурных решёток в плоскости волн накачки в модуле пространственного спектра объектной волны наблюдаются два провала, положения которых определяют пространственные частоты волн накачки (рис. 3 б ). По сравнению с записью одной температурной решётки, когда минимальное значение модуля пространственного спектра в провале равно нулю, при записи двух решёток минимальное значение модуля пространственного спектра в провале не равно нулю и зависит от угла падения волн накачки на нелинейную среду. Ненулевое значение модуля пространственного спектра в провале связано с записью в среде двух температурных решёток. Так, в точке провала ( к 4 = к 1 ) на нулевое значение пространственного спектра объектной волны A 42 ( к 4 , z = I ) накладывается максимальное значение пространственного спектра объектной волны A 441 ( к 4 , z = I ).

Введём параметр, характеризующий видность провала в модуле пространственного спектра объектной волны

^V = ^{( A} 4max - ^A 4mn )/( ^A 4max ^{+ A} 4min ) ’ ⁽¹⁴⁾ где A_4min = I A 4 ( к ₄ = K 1 , z = l )| - значение модуля пространственного спектра в провале (на пространственной частоте первой волны накачки), ^A 4max = I A 4 ( к 4max , z = l )I — ближайшее к провалу наибольшее значение модуля пространственного спектра при условии к 4тах > к 1 , к _4тах = I к _4max| - пространственная частота, на которой достигается наибольшее значение пространственного спектра.

Для анализа пространственной селективности четырёхволнового преобразователя излучения в плоскости волн накачки введём ширину провала (∆κ)

^Ак=|^к 41 х ^-к 42 х | ’ ⁽¹⁵⁾ где κ 41 x и κ 42 x – пространственные частоты в области провала, которые находятся из решения уравнения

1 A (^ 2 X , к 41,2 у = 0, z = I )| = ( A 4max + A 4^/ 2 . (16)

При падении волн накачки на нелинейную среду под одинаковыми углами увеличение угла падения приводит к монотонному уменьшению значения A 4max . Уменьшается видность (рис. 4, кривая 1) и ширина провала в модуле пространственного спектра объектной волны (рис. 4, кривая 2).

Изменение фазы пространственного спектра объектной волны (φ) при учёте как одной, так и двух температурных решёток определяется проекцией волновой расстройки на ось Z и при к 1 = -к 2 хорошо описывается параболическим законом

ф ( к 4 ) = (2 к ) . ( к 2 -к 4 ). (17)

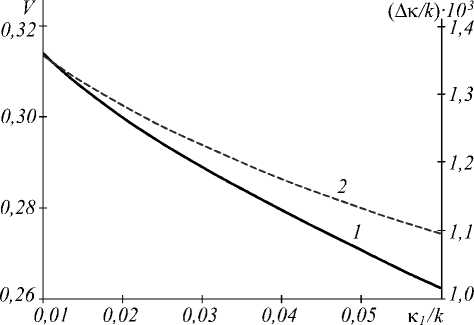
Рис. 4. Зависимость видности (1) и ширины провала (2) от угла поворота волн накачки при k I =5000

3.    Изменение во времени пространственного спектра объектной волны

При нестационарном четырёхволновом взаимодействии на временную зависимость пространственного спектра объектной волны существенное влияние оказывает временная динамика решёток концентрации частиц [19].

Как и изменение температуры, представим изменение концентрации в виде суммы быстро (δ C 31 , δ C 32 ) и медленно (δ C 0 ) меняющихся в зависимости от координат составляющих

8 C ( r, t ) = 8 C ₀ ( z , t ) + 8 C 31 ( F , t ) + +8 C 3’1 ( r, t ) + 8 C ₃₂ ( r,t ) + 8 C ₃ * ₂ ( F , t ) .

Быстро меняющиеся составляющие концентрации разложим по гармоническим решёткам

^

^{8 C} 31,2 ⁽ r , t ) = J ^{8 C} 31,2 ( ^к C 1,2 , z , t ) ^X

-^

X e ^x p ( ^- i ^к C 1,2 P ) di e C 1,2 .

Здесь 8 C 31 ₂ - пространственные спектры концентрационных решёток, обусловленных интерференцией сигнальной волны и волн накачки, к _C 1,2 ( к _C 1,2 _X , к _C 1,2y ) - волновые векторы этих решёток.

Будем считать, что спектры температурных решёток, как и спектры решёток концентрации, меняются во времени.

С учётом разложения температурных и концентрационных решёток по гармоническим решёткам система уравнений (2) – (3) перепишется следующим образом d8 C31,2 (к C 1,2, z, t ) = dt        "

= D 22 ^ d z 2 ^{— к} C 1’2 ^ ^{8 C} 31’2 ^(к C 1’2 , z , t ^{) —}

• -Y[( k1,2z - k3z ) +кC1,2 ] X

^X- A 1’20 ( t ) ^ A 3’o ( ^к 3 , t ) e ^X P [^- i ( k 1,2 z ^- k 3 z ) z ] ’

d8T31,2 (KT 1,2, z’ t) cv p           d t

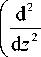
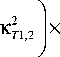
^ (-                  d .2           /- x8 T1,2 (K t 1,2, z’ t ) + D12 I 2 K C 1,2 I 8C31,2 (K C 1,2’ z ’ t ) .

Уравнения (20) - (21) записаны при условии к C 1 ₂ = к T ₁₂.

Будем искать решение системы уравнений (20)– (21) в виде рядов Фурье

⁸ C 31,2 ( ^К C 1,2 ’ z ’ t ) = 0’5 C 01,2 ( ^К C 1,2 ’ t ) ⁺

-                                                 (22)

+E Cm 1,2 (KC 1,2’ t ) COs(nmll)z’ m =1

—

^{8 T} 31,2 ( ^K T 1,2 ’ z ’ t ) = 5 ^Ts 1,2 ( ^K T 1,2 ’ t ) sinC ^ sI ^{l )} z , s =1

где C 01,2 , C m 1,2 , T s 1,2 – коэффициенты разложения рядов.

Подставив (22) в материальное уравнение (20), при отсутствии потока частиц через грани нелинейного слоя ((d 8 C ₃₁ , ₂/d z )| _z = ₀ = (d 8 C ₃₁ , ₂/d z )| _z = , = 0) с учётом начальных условий 8 C ₃₁ , ₂ ( к _{C 12}, z , t = 0) = 0 находим коэффициенты C 01,2 , C m 1,2 . Зная коэффициенты разложения в ряд спектров концентрационных решёток при неизменности температуры на гранях нелинейного слоя, с учётом начальных условий 8 T ₃₁ , ₂ ( к T _ь2 , z , t = 0) = 0 находим коэффициенты T s 1,2 , а значит, и изменение во времени пространственных спектров температурных решёток вида [19]

^{8 T} 31,2 ( ^к T 1,2 ’ z ’ t )

2iYD12 Г(k1,2z k3z ) +кT1,2 1   “     п  '     [

----- —-------------- x 5 sin — z I exp <— cpVn(k1,2z - k3z ) 1         s=1     1   0     [

^{+ к} T 1,2

( t ^-TR ^x

x

T                                                    .

J A 1,20 ^(T ) A 30 ^(к 3 ’ ^{T )x} ( ^к T 1,2 { exp [^— i ( k 1,2 z

^- k 3 z ) ^l ] ^{- 1} } ^{[ 1 -(- 1 )} ] s ^{1 X} exp [^- D 22 ^к 21,2 ^(T-T,)] ^-

—

- ^ I ^{1 -} ( ^{- 1} ) exp [^- i ( ^k 1,2 z ^- m =1

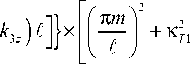
1 -

n m

1 - ( - 1 ) s ⁺‘

I ( k 1,2z - k 3 z ) I J

+ 1 - ( - 1 ) ^ m

s + m      s - m

^x exp ' D 22

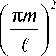
^{+ к} T 1,2

( ^T-T‘ )

d T‘

d T .

J

Для стационарного режима записи температурных решёток ( t ^да) выражения для 8 T ₃₁₂, полученные из (23), совпадают с выражениями для пространственных спектров температурных решёток (11).

Подставив (23) в (9), проведя интегрирование по координате z, получим аналитическое выражение для временной зависимости пространственного спектра объектной волны в виде суммы пространственных спектров двух волн

2 Y D 12 k l ^{( k} 1,2 z ^k 3 z ) ^+к T 1,2 I     d n                        s _r

^A 4 ^, 1.2 ( ^к 4 ’ t ) =-------;--------------------- "T^ ^X-?7 - A 2,10 ( t ) Д^{1 -} ( ^{- 1} ) exp [ ^- i ( ^k 2,1 z ^{- k} 4 z ) ¹ ]} ^X

C p V n 0 ( k 1,2 z - k 3 z )( k 21 z - k 4 z ) I ^{2 d T} s =1^{L                L                   JJ}

1 -

^ s

[ I ( k 2,1 z - k 4 z ) J

^X ( ^K T 1,2 { exP ^[- i ( ^k 1,2 z

1 - ( - 1 ) s ⁺ m

s + m

t

J exP

+ 1 - ( - 1 ) ^s"m

s - m

x exp < - D ₂₂

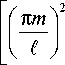
^{+ к} t 1,2

c p ^V

^{+ к} T 1,2

( t ^-T ) ’^x

^x { ^{1 -} ( ^{- 1} ) m ^ex P ^[- i ( ^k 1,2 z ^{- k} 3 z ) ^l ] }

( ^T-T‘ )

d T‘

d T .

T

J- A 1,20 ( ^T‘ ) - A 30 ( ^к 3 ’ ^T‘ ) ^x

—

^{1 -(- 1 ) ]} exp ^[- D 22 ^к T 1,2 ^(t-T ' ^{)] -} 5

m =1

^{+ к} T 1,2

n m

I ( k 1,2 z - k 3 z ) I J

Выражения (13) и (24), описывающие пространственные спектры объектных волн на задней грани нелинейного слоя в схеме с попутными волнами накачки, формально совпадают с аналогичными вы- ражениями для пространственных спектров вырожденного, квазивырожденного четырёхволновых преобразователей излучения на передней грани в схеме со встречными волнами накачки [18, 19]. Меняются выражения для проекции волновой расстройки Δ, разностей проекций на ось Z волновых векторов взаимодействующих волн.

На рис. 5 при условии неизменности во времени амплитуд волн накачки ( A 120 ( t ) = const) представлена временная динамика пространственного спектра объектной волны в плоскости волн накачки. Видно, что образование провалов в модуле пространственного спектра, вызванное наличием явления электрострикции и эффекта Дюфура, запаздывает по сравнению с образованием модуля пространственного спектра, обусловленной ненулевой проекцией волновой расстройки на ось Z . Это связано с зависимостью времени записи температурных решёток от пространственных частот κ T 1,2 . В области провала записываются две температурные решётки, время записи одной из которых определяется пространственной частотой волны накачки, время записи второй температурной решётки стремится к «бесконечности». Сложение пространственных спектров двух объектных волн, соответствующих этим решёткам, и приводит к запаздыванию образования провалов.

\Л'4\, отн.ед.

4"

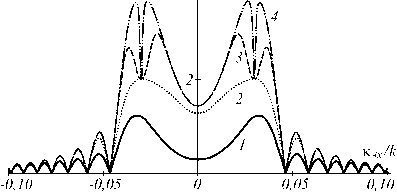
Рис. 5. Пространственные спектры объектной волны в различные моменты времени в плоскости волн накачки с учётом двух температурных решёток при kI =5000, K ix /k = - K 2x /k = 0,03, C p V D 22 /D 11 240 2 Ф22 /I²=10^-5 (1), 10^- (2), 10^-3 (3), 10^-1 (4)

Видность провала в модуле пространственного спектра объектной волны с течением времени возрастает, выходя на установившееся значение (рис. 6).

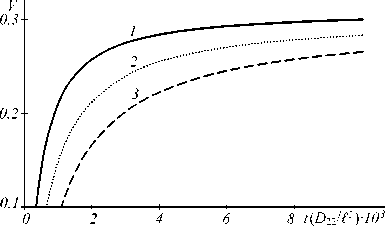
Рис. 6. Зависимость видности провала от времени при k I =5000, C P V D 22 /D 11 2 !(> ' .

K 1 /k = - k₂ /k = 0,02 (1), 0,03 (2),0,04 (3)

Если для характеристики временной динамики провала ввести время образования провала (∆t), как время, в течение которого видность достигает значения 10%, то с ростом угла падения волн накачки на нелинейную среду нормированное время образования провала увеличивается и для углов падения Kix/k=-K2x/k =0,02, 0,03, 0,04 рад составляет соответственно AtD22/1 = 3,445-10-4, 6,49-Ю-4,1,077-10-3.

Скорость изменения во времени видности провала в диапазоне значений от 10 до 20 % с увеличением угла падения волн накачки уменьшается.

4.    Четырёхволновое взаимодействие при больших коэффициентах преобразования

Рассмотрим стационарное попутное четырёхволновое взаимодействие в прозрачной двухкомпонентной среде с учётом того, что интенсивность объектной волны сравнима или даже больше интенсивности сигнальной волны (реализуется режим больших коэффициентов преобразования). В этом случае необходимо учитывать температурные решётки, возникающие при интерференции объектной волны с волнами накачки.

В выражениях для интенсивности и изменения температуры (5) – (6) соответственно добавляются слагаемые A A 4 + A * A 4 + A i A 4 + A * A 4 , 8 T 42 + 8 T 42 + 8 T 4 + 8 T 1 .

Быстро меняющиеся в пространстве составляющие температуры 8T^ (r), как и 8T31,2 (r), разложим по гармоническим решёткам

и

^{8 T} 42,1 ⁽ r ) = j ^{8 T} 42,1 ^(K T 3,4 , z ^)x

—и

X exp ( ^— i ^K T 3,4 P ) ^{d K} T 3,4 .

Здесь 8 T _42j1 - пространственные спектры температурных решёток, обусловленных интерференцией объектной волны и волн накачки, K _{T 3} , ₄ ( к _{T 3} , _{4 x} , к _{T 3} , ₄ y ) -волновые векторы этих решёток.

Уравнения, описывающие изменения пространственных спектров сигнальной и объектной волн, пространственных спектров температурных решёток при квазиколлинеарном распространении взаимодействующих волн примут вид

- dA+--dn {(873,1 +8 T42 )л X dz    n0 dT

x exp [—i (k 2 - k3 z) z ]+(8 T.+8 T4i) .A20X

X exp [-i (k2z - k3z) z ]} = 0,

dA4 . k dn г/s -    - - .a -

+ i       {(8731 + 8742) A2 0 X dz    n0 dT

X exp [-i ( k2z - k4z ) Z] + ( 8T’32 + 8^^4*1 ) A10 X

X exp [-i ( k1 z - k4 z ) z ]} = 0,

2    ^K T 1,2 I ^{8 T} 31,2 ^(K T 1,2 , z ) =

^X exp [^- i ( k_v ,2z ^{- k} 3 z ) ^z ] ² i ( ^k 1,2 z

^^^^^^е

^D^ л_гг „X

1,20 D ₁₁ D ₂₂

d

• — k3, J--+

3 z

+ K T 1,2 +( k1,2 z   k3 z ) ] A3 (K3, z ), d2 dz2

^^^^^^е

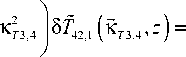
Y D 12

D 11 D 22

^

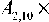
X exp [- i ( k 2,1 _z - k 4 _z ) z ] ² i ( k 2,1 z

- k 4 z ) A +       (29)

+ K T 3,4 +⁽ k 2,1 _z    k 4 z ) ] A 4 ^(K 4 , z ) .

Здесь A ’ ( к 3 , z ) = A 3 ( к 3 , z ) exp [ P ( z )], к _T 3,4 = | к _T 3,4 | = = | ^к 2,1 ^-к 4 |.

На рис. 7 при равных интенсивностях волн накачки ( I 1 = I 2 ) приведены зависимости амплитудного коэффициента преобразования T = | A _4max / A j ₀ 1 и полуширины провала ( Ак 1/2 = | Х 41 x - к 1 x |, к 41 _х > к 1 x ) от нормированной интенсивности волн накачки ( G 1 = k y D ₁₂(d « /d T)1 1 / n о D 11 D ₂₂), полученные при численном анализе систем уравнений (26) – (29). Увеличение интенсивности волн накачки приводит к росту по линейному закону амплитудного коэффициента преобразования, при этом полуширина провала в пределах ±4 % не меняется. Точность нахождения полуширины провала определялась погрешностью при расчёте положения наибольшего значения модуля пространственного спектра. Аналогичный характер зависимости амплитудного коэффициента преобразования от интенсивности волн накачки наблюдается для четырёхволнового преобразователя излучения с попутными волнами накачки на тепловой нелинейности [10].

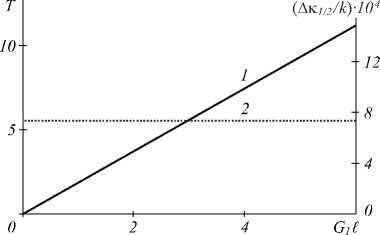
Рис. 7. Зависимость коэффициента преобразования (1) и полуширины провала (2) от интенсивности первой волны накачки при k I =5000, к _1х/k = - K ₂ x /k = 10^-3,1 1 =I 2

Заключение

При малом коэффициенте преобразования для стационарного и нестационарного режимов вырожденного четырёхволнового взаимодействия в прозрачной двухкомпонентной среде с попутными волнами накачки получены аналитические выражения, связывающие пространственные спектры объектной и сигнальной волн. Установлено, что условие фазового синхронизма определяет общий вид модуля пространственного спектра объектной волны, а наличие явления электрострикции и эффекта Дюфура – возникновение в модуле пространственного спектра провалов, положения которых соответствуют направлениям распространения волн накачки. Видность провалов с течением времени возрастает, выходя на установившееся значение. С ростом угла падения волн накачки на нелинейную среду время образования провала увеличивается, а его видность уменьшается.

Рост при I 1 = I 2 интенсивности волн накачки приводит к увеличению по линейному закону амплитудного коэффициента преобразования, при этом полуширина провала не меняется.