Пространственная селективность квазивырожденного четырехволнового преобразователя на резонансной и тепловой нелинейностях при больших коэффициентах отражения

Невырожденный четырехволновой преобразователь излучения позволяет получить волну с обращенным волновым фронтом (ОВФ) с одновременным переводом излучения с одной частоты на другую [1-4]. Именно для невырожденного четырехволнового преобразователя излучения получен коэффициент отражения 5 - 10 ⁵ [5]. До настоящего времени анализ качества ОВФ при квазивырожденном четырехволновом взаимодействии в средах с резонансной, тепловой нелинейностями проводился, как правило, в приближении малого коэффициента отражения, когда не учитываются динамическая решетка, возникающая при интерференции объектной волны и второй волны накачки, самодифракция волн накачки на динамических решетках [6-7].

Анализ характеристик вырожденного четырехволнового преобразователя на тепловой нелинейности, квазивырожденного четырехволнового преобразователя на керровской нелинейности показывает, что величина коэффициента отражения оказывает существенное влияние на соответствие пространственных спектров сигнальной и объектной волн [8-9].

чием тепловой нелинейности. Несомненный интерес представляет изучение качества обращения волнового фронта квазивырожденным четырехволновым преобразователем излучения Ш 1 + Ш ₂ — Ш 1 = Ш ₂ на резонансной и тепловой нелинейностях при больших коэффициентах отражения.

1. Вывод выражений, описывающих квази-вырожденное четырехволновое взаимодействие

Пусть в плоском слое с резонансной и тепловой нелинейностями толщиной I распространяются навстречу друг другу две волны накачки с комплексными амплитудами A 1 и A 2 и сигнальная волна с амплитудой A 3 . В результате четырехволнового взаимодействия Ш 1 + Ш ₂ — Ш 1 = Ш ₂ генерируется объектная волна с комплексной амплитудой A 4 .

Исходные скалярные уравнения, описывающее четырехволновое взаимодействие в нелинейной среде, есть [8]

v2 + k + 2k- — st—2k2^)( a+a+A+A)-о, (1) (       n° dT    1+bi / v2 + k +25 dn st—^k'')(A+A+4+4=0. (2)

^         П 0 dT    1 + bi у             '

Здесь i = AA*, A = ]T Aj j=1

, n 0 – среднее зна-

чение показателя преломления, k 1,2

^ 1,2 n 0

c

волновое число, 5T — изменение температуры, обусловленное выделением тепла при поглощении излучения, а0 = N012 - начальный коэффициент поглощения, N – концентрация частиц, b – параметр, представляющий собой комбинацию сечений поглощения и скоростей релаксации между энергетическими состояниями резонансной среды. В случае среды, моделируемой трехуровневой схемой энергетических уровней c учетом возбужденных синглетного и триплетного уровней, имеем b = ^12(^31 + 823) + С21831 [831 (821 + 8 23 )] ^®1 , где Су и 8у - сечения поглощения и вероятности безызлучательных переходов между i и j энергетическими уровнями.

Уравнение (1) дополняется уравнением Пуассона

Быстро осциллирующие составляющие температуры разложим по гармоническим решеткам

M

8 T 31 ( F ) = J 8 T 1 ( к t 1 , z ) exp ( - i К т 1 Р ) d К t 1 ,

—M

/ X M                X                 x          (5)

8 T 4₂ ( F ) = J 8 T ₄₂ ( K _{t 2} , z ) exp ( - i К _{T 2} p ) d К _{T 2} .

—M

С учетом приближения медленно меняющихся амплитуд волновые уравнения (1)-(2) распадаются на систему уравнений вида

dA ik dn ~     a.

— + —— 8 TA +- A = 0, dz n ₀ dT ⁰¹ ( 1 + bl 0 )

V ² 8 T +---- ^a 0 I ---- _ 0 ,

Л c p v ( 1 + bl )

dA ik dn

— ---—8 T0 A2 — dz   n0dT

^a 0 A = 0, ( 1 + bl 0 ) ² ’

где Л - температуропроводность, c p - удельная теплоемкость, у - объемная плотность вещества. При записи уравнений (1)-(3) не учитывалась зависимость коэффициента поглощения, среднего значения показателя преломления, параметра b от частоты волны.

Будем рассматривать четырехволновое взаимодействие при следующих условиях:

• 1.    в нелинейной среде распространяются четыре волны;

• 2.    справедливо приближение заданного поля по волнам накачки;

• 3.    учитываются динамические решетки, возникающие при интерференции первой волны накачки и сигнальной волны, при интерференции объектной волны и второй волны накачки;

• 4.    учитывается самодифракция волн накачки в сигнальную и объектную волны.

Выражение для интенсивности взаимодействующих волн имеет вид

dA ik dn - a„

—3 + ——8 TA + --- dz n 0 dT 03 (1 + bl0)

A =- k dn 8 T₄₂A

3             421

n 0 dT

ik- dn 8 T* A, ■   a b A,• A A + n0 dT 31 ' (1 + bl0 )2 1

^1

_

ah - - -

-^-T AA 2 A 4 exp( - iAz ),

dAA - ik 2 dn 8 t₀A₄ - , ^a0 ₄ A = i^dn 8 TA + dz n ₀ dT ⁰⁴ ( 1 + bl ₀ ) ⁴ n ₀ dT ³¹

ik —8 T * A

42 2 n 0 dT

_

ah   - - - a0b   Д*Д Д _

2 _T 2 2 A 2 ^A 4 A 2

( ^{1 + bI} 0 )

a. b

—⁰—2- A >12 A 3 exp( - i A z ).

Здесь A = ( k 1 + ^F ₂ - ^F ₃ - ^F ₄ ) _z волновой расстройки на ось Z.

– проекция

Уравнение Пуассона распадается на три

уравнения

V ² 8 T ₀ +

^a 0 I 0

^{Л с}р ^v ( ^{1 + bI} 0 )

=0,

Г d ²              a> A 1 A * ^exp [^{- i} ( k 1 z ^- k 3z ) ^z ]

2 K T 1 ^{8 T} 31 ⁺                     2

( dz )            ^{Л с}р ^v ( ^{1 +} b ¹ 0 )

I = I ₀ + A 1 A ₃ * + A * A 3 + A A 4 + A ₂ * A ₄.

Здесь 1 ₀ = A 1 A * + A ₂ A * . С учетом выражения для интенсивности изменение температуры можно представить в виде суммы быстро ( 8 T „, 8 T 42 ) и медленно ( 8 T O ) меняющихся в зависимости от координат составляющих

8 T = 8 T ₀ + 8 T 31 + 8 T 4 ₂ + 8 T ₃ * + 8 T ₄ * ₂ .

Пусть волны накачки плоские

^A 1,2 ( r ) = A 1,2 ( z ) exP ( - ^ik 1,2 r ) .

Сигнальную и объектную волны разложим по плоским волнам

Г d ²              a> A?A * ^exp [^{- i} ( k 2 z ^{- k}4z ) ^z ] __n

2 ^K T 2 ^{8 T} 42 ⁺                    2          0

( dz       )             ^{Л с}р ^v ( ^{1 +} b ¹ 0 )

Системы уравнений (6)-(7) записаны при условии что i<_T 1 = A 1 -i< ₃ , i<_{T 2} = i< ₂ - ^ 4 .

Системы уравнений (6)-(7) необходимо дополнить граничными условиями: на амплитуды взаимодействующих волн

M

Aj (r )= J Aj (Kj, z) exP (-КуР - i^z) d Ку, j = 3,4,(4) —M где p и z - поперечная и продольная составляющие радиус-вектора r .

A ( z = 0 ) = A~ A 2 ( z = / ) = A 2 0 ,

A ₃ ( k ₃ , z = 0 ) = A ₃₀ ( a -₃ ) , A 4 ( к ₄ , z = £ ) = 0; (8)

на изменение температуры

8 A , ( z = 0 ) = 8 T 0 ( z = ^ ) = 0,

8 T ₃₁ ( z = 0 ) = 8 T ₃₁ ( z = ^ ) = 0,

8 T 42 ( z = 0 ) = 8 T 42 ( z = ^ ) = 0.            (9)

Граничные условия на изменения температу-

ры записаны при условии неизменности температуры на гранях нелинейного слоя.

Решение первых двух уравнений системы (4) есть

^A 1 ( z ) ^{- A} _w exp [ - Q( z ) ] ,

A2 ( z )- Aoexp [-С2(£) + С 2( z)].

Здесь

^2 (z) - ifl8T„ (z)dz. + Сo(z) , n0 dT0

zz fX

Сo (z) = I [[1 + b^)] P

Сделаем замену A 3 - A 3- exp [- С ₁ ( z ) ] , A ₄ - A 4 " exp [- С ₂ ( k ) + С ₂ ( z ) ] . Тогда уравнения, описывающие изменение пространственных спектров сигнальной и объектной волн по мере их распространения в нелинейной среде, примут вид

нейность отсутствует ( b - O) из (11)-(12), имеем систему двух связанных дифференциальных уравнений третьей степени, описывающих изменение комплексных амплитуд сигнальной и объектной волн, вида

- iGA 4 * exp

d ³ A  .к² a ² A ;

---3³ + ¹ --Г dz     k 1 dz

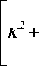
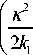
² 1 JV

I 3 y- - 1G_XA 3 exp ( - 2 a z ) -

I dz

к f 1 1 X — — -— z 2 [ k 2 k J

+ 2 ^ ( z - ^ )

d3A:;+i^- dA dz     k2dz

- iGA j exp

2 k 2

.² 1 ,7Л' *

I — z- - iG2 'A£ £ exp [ 2 a ( z - k ) ] -

к f 1 1X z - 2az

2 [ k ₂ k J

.

dA   k dn^Ao(8T +8T1)exp[-i( kz -k z) z]-/'Ь J^expf-ToCz)]+ dz    no al                                   (1+ blo)

■J' b AA A ex' i A- 2 С , ( ^ ) + 2 С , ( z ) ] ,

^{(1 + bl} o )

d| - k ^(Г -8T 'ex'P kz - k4 z) z]   ' ° b A -4 exp[-2С0(?)+2Сo(z)] - dz no al                                    -1 (1+ blo)

. ° b ₁ A o A "A exp [ - i ‘A z ^{- 2} C O ⁽ z ) ] -

^{(1 +} bI o )

Здесь G ₁₂ -

^k 1,2 dn « o / A o \2 n _o dT Л c_p v ^{( 1,} 2 ^{O )}

G ² - G ₁ G ₂.

Наряду с граничными условиями (8) система уравнений (13) должна быть дополнена гра-

ничными условиями

dA ₃

dA ₃ dz

- O, z -k

dA 4

dA 4 dz

^{- O},(14)

Уравнения для пространственных спектров тепловых решеток примут вид

d _-K ^8 1 I ^oAAT exp H- i X k z ^- k z ) ^{z 2 С} 1 ^{z )} ] .d    J ³¹            v _v ( 1 + bl o ) ²

вытекающими из неизменности температуры на гранях нелинейного слоя.

2. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

-o,

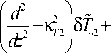
° A A exp [- ( k z - k 4 z ) z - 2 С ;(k) + 2 С 0 ( z ) ] ^ c p ^v( ^{1 + bI} o ) 2

=o.

В параксиальном приближении при распространении плоских волн накачки строго вдоль оси Z имеем

На рис. 1 при равных интенсивностях волн накачки приведены характерные зависимости от нормированной интенсивности волны накачки амплитудного коэффициента отражения ( R ) объектной волны и амплитудного коэффициента пропускания ( K ) сигнальной волны

,      ,       K2

k, - k, -

1 z     3 z 2 _k 1 ,

^k 2 z ^{- k} 4 z ^-

K ²

-

2 k ₂ ^,

A 4 (/ ? - O, z - O ) .A ; ( £ - o, z - o )

K -

A3 (/r - O, z - £) JA^/K - O, z - O)

A-^{K 2} [-

2 [ k 1

T k 2 7

где K = |KT1 =|KT2I = |Кз| = |K4|.

Системы уравнений (11) – (12) с учетом граничных условий позволяют численными мето-

дами однозначно определить связь между пространственными спектрами сигнальной и объектной волнами при наличии как резонансной, так и тепловой нелинейностей.

В частном случае, когда резонансная нели-

полученные путем численного анализа систем уравнений (11)-(12). При условии k ₁ >  k ₂ с увеличением интенсивности волн накачки вначале наблюдается возрастание, а затем уменьшение коэффициентов отражения и пропускания. При k ₁ <  k 2 на максимуме кривой зависимости коэффициента отражения от интенсивности волн накачки наблюдается появление дополнительных максимумов. Причем величина этих дополнительных максимумов возрастает с увеличением разности частот сигнальной и объектной волн.

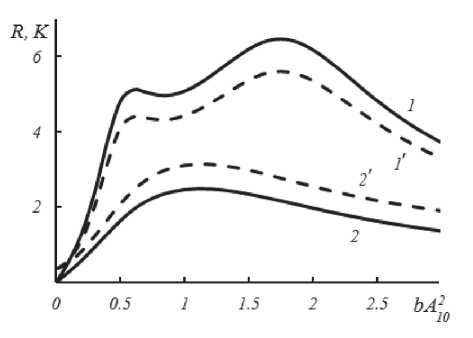
Рис. 1. Зависимость амплитудных коэффициентов отражения (1, 2) и пропускания (1', 2') от интенсивности волн накачки при k I - 5 -10 3 , а/ - 1 , к 1 - 0.75 к 2 (1,1'), к 1 - 1.5 к 2 (2,2')

При условии к 1 >  к ₂ и фиксированных параметрах нелинейной среды, интенсивности волн накачки увеличение пространственной частоты объектной волны приводит к монотонному уменьшению модуля амплитуды пространственного спектра объектной волны. Аналогичная зависимость модуля амплитуды пространственного спектра объектной волны наблюдается и при к 1 <  к ₂ в области монотонного увеличения или уменьшения коэффициента отражения с ростом интенсивности волн накачки. В области изменения интенсивности волн накачки, в которой наблюдаются дополнительные максимумы коэффициентов отражения и пропускания, происходит смещение максимума пространственного спектра объектной волны в сторону больших пространственных частот.

Для характеристики пространственной селективности четырехволнового преобразователя при условии монотонного уменьшения с ростом пространственной частоты модулей пространственных спектров объектной и сигнальной волн введем полуширины полос пространственных частот объектной ( Д к ) и сигнальной ( Дк' ) волн, определяемые из выражений [8]

| A (К-ДК, z - 0)|-2| A (К - 0, z - 0)| ,

| ~ (к-ДК, z - К)-1 А~3( (К - 0, z - К) .

Качество обращения волнового фронта обратно пропорционально полуширине полосы пространственных частот. Наблюдается корреляция между изменением в зависимости от интенсивности волн накачки коэффициентов отражения, пропускания и полуширинами полос пространственных частот. Нормированные полуширины полос пространственных частот

Дк 1 - Дк

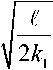
, ^ДК 2 ^-ДК     ,

с ростом ко-

эффициента отражения (пропускания) уменьшаются (рис. 2.a). Причем, чем быстрее с ростом интенсивности увеличиваются (уменьшаются) коэффициенты R и K , тем сильнее изменяются значения величин Дк 1 и Дк ₂. Увеличение при равных интенсивностях волн накачки разности их частот приводит, как правило, к уменьшению коэффициентов отражения и пропускания, а значит к меньшему изменению полуширин про-

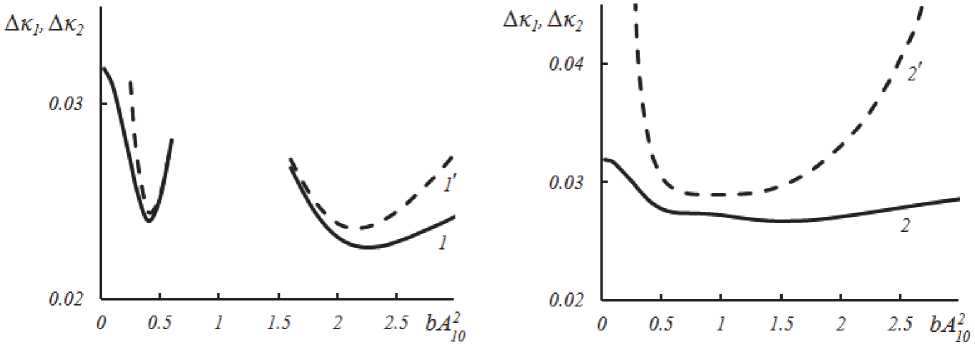
а)                                               б)

Рис. 2. Зависимость полуширины полосы пространственных частот объектной (1, 2) и полуширины полосы пространственных частот сигнальной волн (1', 2') от интенсивности волн накачки при к К - 5 -103, а 0К - 1, А20 - А20; а - к 1 - 0.75 к 2; б - к 1 - 1.5 к 2

странственных частот объектной и сигнальной волн по мере изменения интенсивности волн накачки (рис.2.б).

На рис. 3 в случае наличия только тепловой нелинейности ( b = 0 ) приведены зависимости коэффициента отражения, полуширины полосы пространственных частот объектной волны от интенсивности волн накачки, полученные при численном анализе системы уравнений (13). Если при вырожденном четырехволновом взаимодействии увеличение интенсивности волн накачки приводит к росту коэффициентов R и K и к уменьшению величин Ак ₁ и Ак 2 , то при ква-зивырожденном взаимодействии увеличение разности частот между волнами накачки приводит вначале к уменьшению скорости изменения полуширин объектной и сигнальной волн с ростом интенсивности волн накачки. При дальнейшем увеличении разности частот волн накачки скорость изменения Ак ₁ и Ак 2 с увеличением интенсивности волн накачки, изменив знак, вновь возрастает.

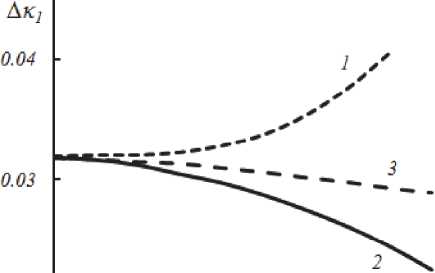
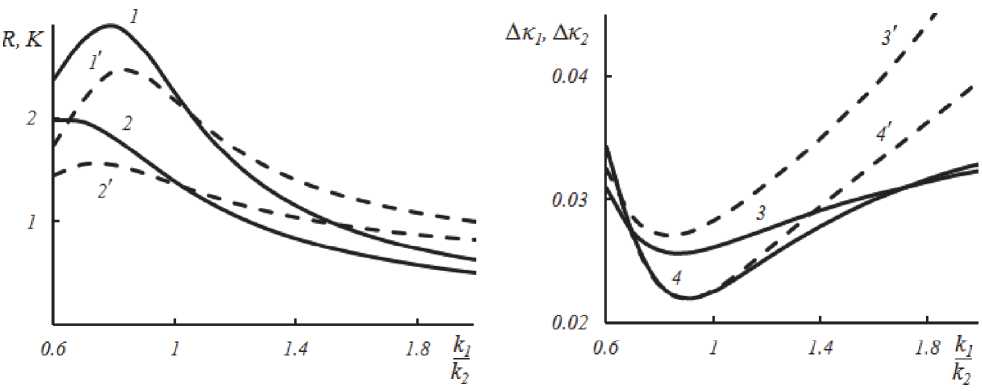
В отличие от квазивырожденного четырехволнового преобразователя на керровской нелинейности, у которого при равных интенсивностях волн накачки с ростом частоты второй волны накачки коэффициент отражения монотонно увеличивается [8], для квазивырожденного четырехволнового преобразователя на тепловой нелинейности такая зависимость наблюдается лишь при малой интенсивности волн накачки. С ростом интенсивности волн накачки (а значит и коэффициента отражения) на кривой зависимости коэффициента отражения от соотношения между волновыми числами волн накачки наблюдается максимум, а на кривой зависимости полуширины полосы пространственных частот объектной волны – минимум, положения которых с увеличением интенсивности волн накач- ки сдвигаются в сторону больших значений отношения волновых чисел (рис. 4).

Как отмечалось в работе [9] на характеристики четырехволнового преобразователя излучения при больших коэффициентах отражения влияют два процесса: самодифракция волн накачки и перекачка энергии из сигнальной волны в объектную и наоборот. С увеличением интенсивности волн накачки процесс самодифракции волн накачки приводит к росту, а процесс перекачки энергии к уменьшению полуширин полос пространственных частот. При квазивырожден-ном взаимодействии наличие дополнительной волновой расстройки приводит к уменьшению влияния на характеристики четырехволнового преобразователя процесса перекачки энергии из сигнальной волны в объектную и наоборот, и, как следствие этого, к росту значений величин Ак ₁

и Ак2 с увеличением интенсивности волн накачки. Подбором соотношения между интенсивностями волн накачки можно частично скомпенсировать волновую расстройку, связанную с отличием частот взаимодействующих волн. Численный анализ уравнений (13) показывает, что при выполнении условия к 1 A20 = к 2 A220 (15) зависимости от интенсивности волн накачки коэффициентов R и K, полуширин полос Ак1 и Ак2 для вырожденного и квазивырожденного четырехволновых преобразователей излучения на тепловой нелинейности совпадают.

При квазивырожденном взаимодействии на керровской нелинейности условие (15) означает отсутствие в волновой расстройке составляющей, связанной с интенсивностями волн накачки.

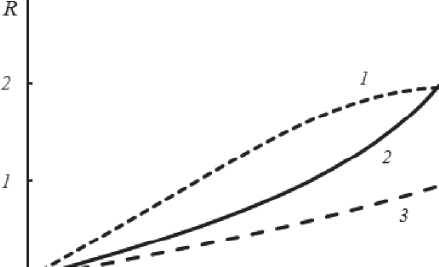
--------1------------------1------------------1------------------1------------------ 0.02 ------------------¹------------------¹------------------¹------------------¹---------------- 0      20      40      60      80 G€        0      20      40      60      80 G€

а)                                                         б)

Рис. 3. Зависимость амплитудного коэффициента отражения (а) и полуширины полосы пространственных частот объектной волны (б) от интенсивности волн накачки при наличии только тепловой нелинейности при к £ = 5 -10 3 , и ₀ £ = 1, к 1 = 0.5 к 2 (1), к 1 = к ₂ (2), к 1 = 1.5 к ₂ (3)

б)

а)

Рис. 4. Зависимость от соотношения между волновыми числами волн накачки а) амплитудных коэффициентов отражения (1, 2) и пропускания (1', 2'); б) полуширин полос пространственных частот объектной (3, 4) и сигнальной (3', 4') волн при k t - 5 -10 3 , a „ I - 1, G t - 80 (1,1', 3, 3'), G t - 100 (2, 2', 4,4')

Отметим, что при наличии как резонансной, так и тепловой нелинейностей выполнение условия (15) не приводит к совпадению характеристик вырожденного и квазивырожденного четырехволновых преобразователей излучения. Это условие может быть использовано для определения области интенсивности волн накачки, в пределах которой коэффициент отражения четырехволнового преобразователя с учетом резонансной и тепловой нелинейностей максимален, а полуширина полосы пространственных частот объектной волны минимальна.

В качестве примера рассмотрим четырехволновое взаимодействие в слое толщиной t - 0.02 см водно-спиртового раствора эозина ( dn- - 4 - 10 "⁴ град^-1, n ₀ - 1.36 , Л c v - 3 - 10 "³ dT                  ^{0             p}

Дж/(см-с-град), N - 5 - 10¹⁸ см^-3, 0 12 =0 21 - 10¹⁷ см², 3 ₂₁ - 3.57 - 10⁸ с^-1, 3 ₂₃ - 7.6 - 10⁸ с^-1, 3 ₃₁ - 10³ с^-1) [10]. При вырожденном четырехволновом взаимодействии на длине волны 532 нм с равными по интенсивности волнами накачки (52 Вт/ см²) коэффициент отражения R - 50 , а полуширина полосы пространственных частот объектной волны А к ~ 29 см^-1. При квазивы-рожденном четырехволновом взаимодействии, когда в качестве второй волны накачки используется излучение на длине волны 632 нм, коэффициент отражения уменьшается до значения R - 6 , а полуширина полосы пространственных частот объектной волны увеличивается до А к ~ 92 см^-1.

ЗАКЛЮЧЕНИЕ

• 1.    Для квазивырожденного четырехволнового преобразователя на резонансной и тепловой нелинейностях наблюдается корреляция между зависимостями от интенсивности волн накачки коэффициента отражения (пропускания) и полуширины полосы пространственных частот объектной (сигнальной) волны. Рост коэффициента отражения приводит к уменьшению полуширины полосы пространственных частот.

• 2.    При наличии только тепловой нелинейности с увеличением разности частот волн накачки происходит изменение характера зависимости полуширины полосы пространственных частот объектной (сигнальной) волны от интенсивности волн накачки: уменьшение полуширины полосы пространственных частот с ростом интенсивности меняется на увеличение.

Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры России» на 2009-2013 годы (Государственный контракт № 14.740.11.0063).