Пространственная структура азимутально-мелкомасштабных МГД-волн в одномерно-неоднородной плазме конечного давления с кривыми силовыми линиями

Ultra-low frequency (ULF) waves with large azimuthal wave numbers are observed in near-equatorial regions of the magnetosphere, characterized by a relatively high plasma pressure (the ratio of plasma pressure to magnetic pressure β~1) and significant field line curvature [Agapitov, Cheremnykh, 2011; Moiseev et al., 2016; Rubtsov et al., 2018a] . These waves are generated due to injection of high-energy particles into plasma [Guglielmi, Zolotukhina, 1980; Mager, Klimushkin, 2007; Kostarev, Mager, 2017] . In recent years, azimuthally small-scale waves have been extensively studied using radars [Berngardt, 2017; Chelpanov et al., 2018] and satellites [Leonovich et al., 2015; Mager et al., 2018; Takahashi et al., 2018] . The development of the theory of such waves is a topical problem of space plasma physics because they may be responsible for the acceleration of charged particles in the magnetosphere [Ukhorskiy et al., 2009] and can serve as triggers of substorms [Rae et al., 2014] .

As known, there are three MHD modes: Alfvén, fast magnetosonic (BMS), and slow magnetosonic (SMS). When accounting for plasma inhomogeneity, these modes are coupled, i.e. they cannot propagate independently of each other. The simplest model of the magnetosphere is a one-dimensionally inhomogeneous model with straight field lines, which takes into account only magnetospheric inhomogeneities across magnetic shells (box model) [Southwood, 1974; Chen, Hasegawa, 1974; Mazur, Chuiko, 2013]. This model has established the Alfvén resonance, the essence of which is as follows. Processes at the magnetospheric boundary generate a FMS wave propagating deep into the magnetosphere. On a surface located inside the magnetosphere, the FMS wave is reflected. Part of FMS energy, however, tunnels and with an exponentially decreasing amplitude propagates deeper into the magneto- sphere until it reaches a magnetic surface, where its frequency coincides with the local frequency of the Alfvén wave. On a respective magnetic surface there is a sharp peak of the Alfvén wave amplitude. The azimuthal wave electric field component as well as the radial magnetic field and plasma velocity components have a logarithmic singularity; the radial electric field component and the azimuthal magnetic field and velocity components, a pole singularity.

This model in the case of finite pressure plasma has been generalized by Yumoto [1985] ; the author has shown that in plasma with β>0 there should also be a resonance on a magnetic surface, where the wave frequency is equal to the local frequency of SMS waves. The singularity on this surface appeared to be the same as on the Alfvén resonant surface.

In the azimuthally small-scale limit, the FMS role can be ignored because its transparent region turns out to be localized in the immediate vicinity of the magnetopause and only an exponentially small part of FMS energy enters the magnetosphere [Guglielmi, Potapov, 1984] . Two major MHD modes in this case are Alfvén and SMS coupled due to the field line curvature [Southwood, Saunders, 1985; Walker, 1987; Cheremnykh, Parnowski, 2004] . The spatial structure of these modes in a two-di-mensionally inhomogeneous magnetospheric model with irregular field line curvature has been studied in [Klimushkin, 1997; Klimushkin, 1998; Klimushkin et al., 2004] . It has been shown that in the model there are two regions of mode localization — Alfvén and SMS transparent regions. Each of them is bounded on one side by the resonant surface, where the radial wave vector component k r becomes infinite, and by the reflecting surface, where k r becomes zero. In each of the transparent regions, k r ² >0. We have studied the wave field singularities on resonant surfaces. On the Alfvén resonant surface, the

This is an open access article under the CC BY-NC-ND license

singularity was the same as in one-dimensionally inhomogeneous plasma. On the SMS resonant surface, the singularity, however, appeared to differ from that in the one-dimensionally inhomogeneous model.

It is still not quite clear to what extent we can trust the results obtained in [Klimushkin, 1997; Klimushkin, 1998; Klimushkin et al., 2004] since the mathematical methods for studying the two-dimensionally inhomogeneous magnetospheric model are not sufficiently advanced. To solve these difficulties, Cheremnykh et al. [2014, 2016] have examined the cylinder magnetospheric model, which considers magnetic surfaces to be concentric cylinders and takes into account only the inhomogeneity across the magnetic surfaces. Despite its relative simplicity, this model keeps such basic features of magnetospheric plasma as radial inhomogeneity and field line curvature. At the same time, it can avoid some mathematical difficulties specific to more realistic two-dimension-ally inhomogeneous models. The cylinder model was also used to study MHD waves in the solar corona [Kaneko et al., 2015, Cheremnykh et al., 2018] .

The main results of earlier studies [Klimushkin, 1997; Klimushkin, 1998, Klimushkin et al., 2004] in terms of Alf-vén modes have been confirmed. Cheremnykh et al. [2014, 2016] did not, however, treat the SMS spatial structure in detail. The questions about the match between the cylinder model and the one-dimensional model of the magnetosphere studied in [Yumoto, 1985] were not addressed either. In this paper, we fill this gap.

1.    GENERAL EQUATION

ULF waves are usually described using the system of MHD equations:

P d' -^{v P +} C [ J ^x B ] ■ | *v ( p7. ) = o,

J = — [vx B ] ,1 — = -[vx E ] , 4 n ^{[     ]} c d t     ^{[      ]}

d — = o, E =—Lx B dt pY              c [

where v, J, B are speed, current, and magnetic field; p, P are plasma density and pressure; E is the electric field; γ is the heat capacity ratio, — = — + (vV). Linearizing sys-dt   dt tem (1), obtain

p ° = d T ⁼ -V P ⁺ 1 ( [ J ¹ x B o H J o x B ¹ ] ) ,   (2)

1 ⁵ B i c d t

-[Vx E i ] ,

a — d t

- ( ui -V ) — o -Y — ° ( V. V1 ) ,

E 1 =- ¹ [Ui x B o o ] ,

where quantities marked with 0 represent equilibrium values v, p, P, J, B, E; and those marked with 1, small deviations from equilibrium.

Following [Cheremnykh et al., 2018] , we consider the one-dimensionally inhomogeneous cylinder plasma model in which magnetic field lines are concentric circles and all equilibrium values depend only on the radial coordinate r — circle radius (Figure 1).

The coordinate y , directed along the system symmetry axis plays a role of an azimuth coordinate in the magnetosphere. In this model, the magnetic field B 0 =(0, B 0φ ( r ), 0) and plasma pressure P 0 ( r ) satisfy the equilibrium condition

B o ² 4 n r

•

Consider a monochromatic wave with a frequency ω. Due to the system symmetry in coordinates φ and y, the plasma velocity can be written as i (-to t+k y+NФ)

v 1(r,t) = V1(r)ev     y^ ,’, where ky is the azimuthal wave vector component, N is the natural number. The role of the azimuthal wave number m in the cylinder model of the magnetosphere belongs to m=k yr. The value k||=N/r can be regarded as an analogue of the field-aligned wave vector component.

Then motion equation (2) can be written for the components as

Bo B 1ф   ₄ BB

• -    г p_o to d_x r =d _r 5 P - 2-- + ik —^o— ,

4n r      4n r

BBB

• - iPo toЦф =-ikl 5P + iki —.--— 5r (rBo),

4n

, .      kk Bo B 1 y

• -    iPo to Ц y = -iky 5 P + i ----.

r 4n

Here d_r = d / d r , and 5 P is the perturbation of the total pressure (the sum of plasma and magnetic pressures):

5 P = — + B ^ B ¹ » .

• ¹    4n

  

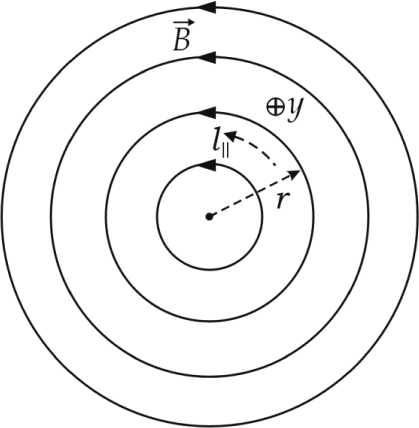
  Figure 1. One-dimensionally inhomogeneous cylinder model

  
  

  Equation (4) yields

  8 P = — i ^r д_гр — i P х to             to

  ^х | - ⁵ r ( r 4 r ) ⁺ ik y'' y ^{+ ik} 'Y,

  
  

  ₊ B o ^В 1ф

  4п

  
  
  
  

  .

  
  

  After transformations in view of (7), we get:

  
  

  the components ^ 1ф and n ty are expressed through u i r and δ P as follows:

  p o ( to² — to 2 ) Цф = ik to ⁽4 8 P — 2p o ^ Ц r ) ,

  I «A           ^r J      (15)

  p o ( to² — to 2 ) V- y = ^iky to ^{8 P .}

  
  

  8 P =

  
  

  to²

  
  

  —

  
  

  to A ( r )

  
  

  to² — to 2 ( r )

  
  

  ( to²

  I to 2

  
  

  ^— ® 2⁽ r ) I — to ( r ) J

  
  

  х

  
  

  1                   2    % to² — to 2 ( r )

  - ⁵ _r ( r d_{1 r} ) + 2    ²  — —---s^

  r              2Л + г; r to² — to 2 ( r )

  As     c

  
  
  
  

  where    v_A = -7—, 'V = Y—, 4 =

  ^4лр о        V ^po       7^UA + 42

  (10) are the Alfvén, sonic, and slow magnetosonic speeds,

  
  

  Note that in the magnetosphere the component u i y directed along the binormal to field lines plays a role of the azimuthal velocity component; and the component и 1ф , a role of the field-aligned component. As readily seen from (15), the field-aligned velocity component in contrast to the radial and azimuthal components disappears when the plasma pressure tends to zero (i.e. when U a ^0).

  
  

  ^to A ^{( r} ) = k ^ua ,  to ^{( r} ) = k ч, to ^{( r} ) = k ч,

  (''A+-;)( k + k y )

  to ±⁽ r ) =---------------------^х

  
  
  
  

  (

  х 1 ±

  
  

  i-- ⁴—

  1   (• A +• 2 ) 2 ( k 2 + k y ) J

  
  

  2. ONE-DIMENSIONAL CASE: NEGLIGIBLE FIELD LINE CURVATURE

  In order to compare with the results obtained by the cylinder model, we consider first the case of parallel straight field lines (box model) discussed in [Yumoto, 1985] . Given x_c = 0, (14) yields an equation for MHD modes [Yumoto, 1985] :

  
  

  Below we show that the frequencies ω A and ω c correspond to Alfvén and SMS resonances; frequencies ω ± , to FMS and SMS reflecting points respectively. To the azimuthally small-scale case corresponds k y >> k || . In this case, the expressions for ω ± reduce to

  to+=( to + to)(k2 + ky),

  I to I

  to2 = to2 i + c .(13)

  —c

  I ^to+ J

  
  

  ^d r ( ^uA⁺ ч² )

  
  

  ( ^to2 ^{— to}A )( ^to2 - ^to2 )          1

  /₂ 2W 2    2 A ^po ^d r ^У1 r ⁺

  ( to — to . )( to — to _—)

  
  

  ^{+ p}o ( ^to2 — ^toA ) ч r = ⁰ .

  
  
  
  

  In this equation there are four specific points determined by conditions

  
  

  to² = to 2 ( r ), to² = to 2 ( r ), to² = to^- ( r ), to² = to 2 ( r ).

  
  
  
  

  If we now substitute δP from (9) in (7), we can derive a differential equation describing the spatial structure of Alfvén, FMS, and SMS waves:

  
  

  The solutions of these four equations are the points with coordinates r c (ω), r – (ω), r A (ω), and r + (ω) respectively. At small values of the parameter β and for transversely smallscale oscillations ( k y >> k || ) between respective frequencies there are relations

  
  

  ^d r (to⁺ to)

  
  

  ( to² — to A )( to² — to 2 ) p_o

  
  

  ( to² — to 2 )( to² — to 2 ) r

  
  

  ^d r ( ^r 4 r ) ^— 2~ ^х

  
  

  ( to² — to 2 )( to² — to 2 )

  "r  p o^A    _{2     2     2}

  ( to — to₊ )( to — to_ )

  + p 0 ( ^to2 ^{— to}A ) Ц r ^{— 2} P o X p X c4 r +

  ₊₄ p 0 X 2 ^to2 kyx^ r ₌₀

  ( to² — to 2 )( to² — to 2 )

  
  

  to_cA<^ to₊.

  In this case, throughout most of the magnetosphere the functions to 2 ( r ), to 2 ( r ), to 2 ( r ), to 2 ( r ) are decreasing [Moore et al., 1987] . Hence, the point r c should be the closest to Earth, followed successively by r – , r A , and r + (Figure 2).

  
  
  
  

  Here X с ( r ) = -I/ r is the function of field line curvature, x p ( r ) = P 0 ^- d_r P is the radial scale of plasma pressure variation. This equation coincides with that derived in [Cheremnykh et al., 2014] , but is written in a more clear form.

  
  
  

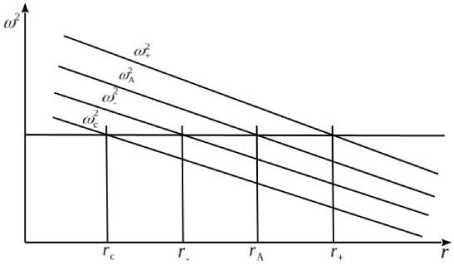
  Figure 2. Graphical solution of Equations (16) and magnetic surfaces (one-dimensional model)

  
  

  Given the radial velocity component, from Equation (9) we can find the total pressure perturbation δP. Next, with (7)

  
  

  First, examine the region | ю - ю_с |, | ю - ю | л, corresponding to the SMS transparent region. In this region, Equation (16) reduces to the form

  
  

  d r

  
  

  P o

  
  

  ® 2_- ® c2 ( r ) ю² - ю 2 ( r )

  
  

  ^d r 4 r

  
  

  — P o ( k ² + ^k2 ) 4 r = °.

  
  
  
  

  If we solve this equation in the WKB approximation, the radial wave vector component k r ( r , ω) will be determined from

  
  

  ^k r ( r , ю) = ^- ( k² + к ² )

  
  

  ю² - ю² ( r )

  ^.

  ^{ю -} ®c ⁽ r )

  
  
  
  

  In the vicinity of the SMS resonance point r ® r c , we can employ the linear expansion ю² - ю 2 ( r ) = ю 2 r—— , where l =-- ^{ю (} r ^c )   is the

  cc     c

  ^c                        [ ®^{2 (} r c ) ]

  typical scale of magnetospheric parameter variations. The l c value is of the same order as L . Then, Equation (18) takes the form

  ^{- 1}

  d 2₄ r +----d r V1 r --— ц r = 0.              (20)

  r - r      r - r

  cc

  
  

  Figure 3 plots к ²( r , ю) as a function of to ² . Formula

  
  

  (19) shows that at r c and r – k r becomes infinite and zero respectively. These points can therefore be called the SMS resonance point and the SMS reflecting point. The region between them, where к 2 > 0, may be referred to

  
  

  Here X с = ( k y l_c ) " '

  
  

  ^c is the SMS wave length near ^Ю c ^{- ю} -

  
  

  the resonant surface (point) r c . The solution of this equation is zero-order Bessel functions

  
  

  as the SMS transparent region.

  The applicability of the WKB approximation to the SMS-wave localization region deserves a separate discussion. The WKB approximation can be used when a transparent region covers many wavelengths. A necessary (but insufficient) condition of this phenomenon is the presence of a large parameter in a wave equation. In the case of Equation (18), the large parameter is naturally considered to be k y .

  As follows from (13), the very difference ю² - ю 2 is,

  
  

  1 r

  
  

  = ^ K 0

  

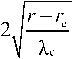
  A

  ^{+ y}2 I 0

  
  
  
  

  where 1 and 2 are arbitrary constants. Write the asymptotic behavior of this solution for | r - r _c |

  
  
  
  
  
  
  

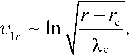
  however, inversely proportional to the square of this quantity:

  
  
  
  

  2      2       2

  ю - ю_c = ю_c

  
  

  ² с

  
  

  Thus, in the immediate vicinity of r c the solution has a logarithmic singularity. This point is the SMS resonance point. When bypassing the logarithmic singularity to r – r c <0 there occurs a jump i π/2:

  
  

  ^ky a\ ⁺ '2 .

  
  

  Thus, with increasing k y the transparent region narrows. As readily seen, the applicability condition of the WKB approximation has the form

  
  
  

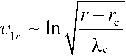
  iin

  .

  
  
  
  

  Lk y

  
  

  ²         с ²

  
  

  к. ’ ''2 + 42

  y As

  
  

  1,

  
  

  With (15) it is easy to determine the behavior of the other two plasma velocity components too. The field-aligned (along the external magnetic field) velocity component has a pole singularity:

  
  

  where L is the typical scale of radially inhomogeneous plasma. Thus, the WKB approximation is applicable only to a weakly inhomogeneous plasma when L is very large.

  
  

  ^ 1ф

  
  

  X c

  r - r _c

  
  
  

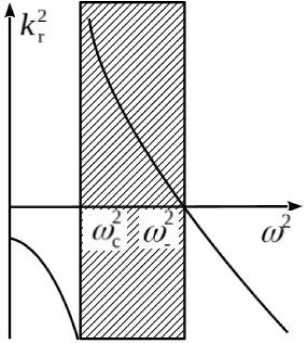
  Figure 3. Squared wave vector component as a function of squared frequency in an SMS transparent region (one-dimensional model)

  
  

  The same is true of the component , directed along the binormal to magnetic shells:

  
  

  X c r - r c ^.

  
  

  The electric and magnetic field components will also have the singularities:

  X_r                . I r - r

  E 1 r ~ E 0       , E 1 y ~ E 0 lnA ^-^   , ^Е 1ф = ⁰ ,

  ^{r -} r c               V X c      ^Ф

  F = F F ~ F ^{X c}

  E 1 r    E 1 y   0, ^Е 1ф    E °        .

  r - r_c

  
  

  Now find the solution near the SMS reflecting point r — when |ю - ю | с. In this case, Equation (18) can be transformed into

  
  

  5 2ц r --— 5 r v, r ^-X - 3 ( r ^- r _ ) ц r = °.           (24)

  r - r -

  
  

Here, it is denoted

X - 3 = m 2 ( m 2 - m 2 ) -p , l_ = - m 2 / [ m 2 ( r_ ) J . This equation is for derivatives of Airy functions. Its general solution is

I r — r I        | r — r гл = a Ai      -  + b Bi      -

1 r            I X_    J ^- I   X_

.

where a – and b – are constants, Ai and Bi are Airy functions of the first and second kinds. Dashes denote r -de-rivatives. Thus, the presence of the singularity at r – in wave equation (16) does not lead to a solution singularity.

In the region of Alfvén wave localization when m « m_A and m_c<^ m <^ m , general equation (15) reduces to the form

5 r [^m 2 - ^m A ( ^r ) ] 8rrn r - ( k y + k ² ) X х[ю² -^m A ( r ) ] u_xr = 0.

Expanding m2 ( r) in the neighborhood of r®ra up to the first member m2 —mA (rA)®-[mA (rA)] (r - rA), get the equation d 2ц r + — dr r-(ky + k2) ц r = 0 (27) r - rA kr = 2    2 -(k2 + ki2 ).                           (32)

A ⁺

This expression is derived directly from the dispersion equation for FMS [Southwood, 1974] . From (32) we can see that the point r + , where the equality m² — m 2 ( r ) = 0 holds, is the FMS reflecting point because at this point the radial wave vector component becomes zero.

Examine the solution near this point in more detail. Expanding m2 (r) in series in r^r +, m2-©+ (r) «-[m+ (r+)] (r-r+) = m2 r—r+, 1+ get

S 2ц r --— d r ч r + X + ³ ( r - r + ) ц r = 0,         (33)

r - r+ where X-3 = 1J1    +   . A solution of (33) will be

A ⁺ ^s

. , I r - r, I           I r - r v. = aMi--+ + bBi--+

1 r    + I X + J ⁺ I     X +

This solution is regular. As in the case of the SMS reflecting point, the presence of the singularity in the wave equation does not lead to a solution singularity.

representing a modified zero-order Bessel equation. Its general solution is

^U1 r = ^U+ ¹ 0 ( 7 k y + k ² ( ^{r - r} A ) ) ⁺

+V - K 0 ( 7 ^ky 2 ⁺ k ² ( ^{r - r} A ) ) ,

where I 0 ( z ), K 0 ( z ) are modified Bessel functions, , are arbitrary constants. In the vicinity of the Alfvén resonance, this solution has a logarithmic singularity

V1 r - ln [7 k y + k ² ( ^r A ^{- r} ) ] .                       ⁽²⁹⁾

According to the singularity bypass rule, the analytic continuation of this solution to the region r < r A has the form:

3. AZIMUTHALLY

SMALL-SCALE WAVES

IN THE CYLINDER MODEL

Cheremnykh et al. [2014] have derived a differential equation used to find the spatial structure of SMS and Alfvén modes. The question about the SMS spatial structure was not, however, completely answered. Address this question in more detail.

In the azimuthally small-scale case (when kk ), the wave frequency is much smaller than the FMS reflecting one: ωω. Then, differential equation (14) takes the form

^v i r ~^ln [ 7 k y ⁺ k ² ( ^{r -} r A ) ]^- i ⁿ .                  (30)

-d r

( ^m2-^mA)(^m2-^m2)

p⁰ 8 r ( r v, r ) +

The azimuthal velocity component ^ 1y has a pole singularity:

1r                      , r - rA whereas the longitudinal component has no singularities.

Finally, at a sufficiently high frequency of (m ^ m_A )

Equation (16) reduces to the form drP             5 rr + p o4 r = 0.                 (31)

m - m ₊ ( r )

+ — r

A ²

A + Ч²

^U1 r ^d r

( ^ 22 ^ X 1( ^ 21 ^ 1 1

+ k 2

( m² - m 2 )( m² - m 2 ) __q

Here ω 1,2 is the solution of the biquadratic equation

2      2          ^X p^X c I 2      2         2 2 2

^{m - m}A ^{- 2 P}0 ---- l ( ^{m - m} - ) ^- 4 ^Xc^m 4 = 0.

P 0 J

When this equation is solved in the WKB approximation, the squared radial wave vector component is defined by the expression

Write an expression for ω 1.2 :

m 2 2 = ¹ _[( m p + m - 4v c x 2 ) ±

±V ( m p ^- m - ) 2 ^{+ 8} ( m p + m - ) ц² x 2 + 16 Ц⁴ X 4

where it is denoted top = toA +(2 Po/Po) X p X c.

Expression (35) is in complete agreement with the equation obtained in [Cheremnykh et al., 2014] for coupled Alfvén and SMS modes.

If the plasma pressure is not very high and the condition в (Xc / k ) ^ 1, holds, the frequencies «1,2 can be written in the approximate form:

(            ^

to ? = _to2   1 - ^Z . X p ,

I       ^toA     J

^to2 = ^toA ⁺ 4x v ^- P^ A x c x p = ^top ^- 4x 2 ч² .

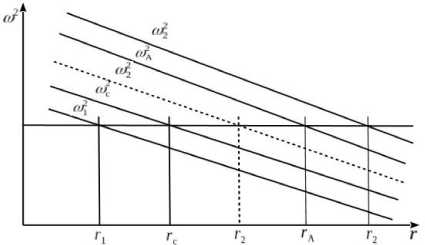
Figure 4. Graphical solution of Equations (40) and magnetic surfaces r c (ω), r 1 (ω), r A (ω), r 2 (ω) (the last one is shown in two cases: ω A < ω 2 and ω A > ω 2 )

Hence, the frequency ω 1 is closer to the SMS resonant frequency ω c ; and ω 2 , to the Alfvén resonant frequency ω A . From these formulas we can also see that the frequency ω 1 has always been lower than the SMS resonant one, ω 1 <ω c . However, the frequency ω 2 may be both higher and lower than the Alfvén resonant frequency.

First, we consider the solution of this equation in the WKB approximation. The squared radial wave vector component is determined from the relation

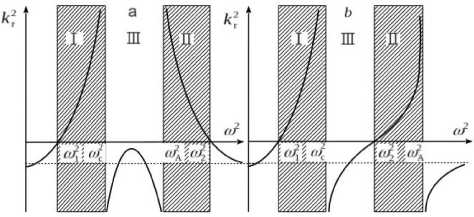
Figure 5. Squared radial wave vector component as a function of squared frequency to ² . When to^to , a and to^to c k_r ² ( r ) have a discontinuity from - да to да , and when passing through points   to 2 ² and   to 2   the function   k_r ² ( r )   changes sign

k , ² ( r , to ) = - k y

to² - to j ( r ) to² - to 2 ( r )

^-^Hr! to2- toA (r)

As we can see, when equalities to=tot (r), to=to2 (r) (40)

hold, the radial wave vector component becomes zero. Hence, the frequencies ω 1 and ω 2 represent reflecting frequencies of SMS and Alfvén modes respectively. The points r 1 and r 2 as solutions of (39) will be called reflecting points of SMS and Alfvén modes respectively. Since throughout most of the magnetosphere the functions ω c ( r ), ω A ( r ), and ω 1,2 ( r ) are decreasing, there is always the inequality r 1 < r c . In the case of ω A < 2 , r A < r 2 ; in the opposite case of ω A >ω 2 , r A > r 2 (Figure 4).

Figure 5 plots the squared radial wave vector component k_r ² ( r ) as a function of the squared frequency « 2 . Panel a corresponds to ω A <ω 2 ; panel b , to ω A >ω 2 .

Numerals I and II denote areas of propagation of SMS and Аlfvén waves respectively. Numeral III refers to frequencies at which wave propagation is impossible. Accordingly, the SMS transparent region is in the range r 1 < r < r c ; the Alfvén mode transparent region, in the range r A < r < r 2 ( a ) and r 2 < r < r A ( b ).

For the Alfvén transparent region the resonant surface r A is also referred to as the toroidal surface; the reflecting surface r 2 , as the poloidal surface [Leonovich, Mazur, 1993]. When k r →∞, field lines seem to slide over unperturbed magnetic surfaces (cylinders in our case); and when k r =0 they oscillate along the normal to magnetic shells.

If an opacity region is much wider than the transparent regions of each of the modes, Equation (35) allows for a further simplification in the Alfvén and SMS transparent regions. Consider the Alfvén transparent region in the case of |to_A - to₂| A, to₂ » to_c, to , for large values of k y . Then Equation (35) reduces to the form

ky. ( r )

-5 r [ to^{2 -} to A⁽ r ) ] 5 r V, r + ky, [ to^{2 -} to 2⁽ r ) ] Ц r = 0, (41)

which coincides with the equation for the Alfvén mode derived in [Cheremnykh et al., 2014] . Since the authors have carried out a sufficiently detailed analysis of the solution of this equation, we do not dwell on it. We note only that near the resonant surface there is still the logarithmic singularity of the wave field as in the one-dimensional case:

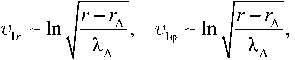
where

^A = ky' к (to! - to2)/to² ,   l_A =- to² /[ to² ( r _A ) 1 . The

y azimuthal velocity component takes the form

1 y

^{r - r} A .

The electric and magnetic field components have the form

E ,r ~ E o -^ A- , E , y ~ E o ln. r r r A , Е 1ф = 0, r ^- , a    '             A

E , _r = E , y = 0, Е ,ф~ E ₀^ .

r - rA

Away from the resonant surface, the behavior of the

wave field appears, however, to be different than in the one-dimensional case. If in the one-dimensional case the Alfvén wave is an isolated resonant peak, in the curved geometry the solution near the resonance point is oscillatory, with the wavelength decreasing as it approaches the singularity. This is also consistent with the results obtained in [Klimushkin, 1997; Klimushkin, 1998; Klimushkin et al., 2004] for the two-dimensionally inhomogeneous magnetospheric model with variable field line curvature and longitudinal inhomogeneous plasma.

In this paper, we focus mainly on the SMS transparent region. Consider the limiting case |ю_с - ю^ю and ω , ω ω , ω . In this case, Equation (35) reduces to the form

The analytic continuation of this solution is:

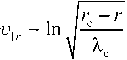
5 r

^ю2 ^{- ю} ( ^r ) L_y ²

2       2            r 1 r          2       2

ю - ю_ ( r )         r Г A ⁺ 4

x ц r a r

®² — ®^{2 (} r ) !   r2 ® 2 — ®^{2 (} r\,    .

2       2 / \     ky 2      2 ( \ ^U1 r    ^U *

to - ю_ ( r )       ю - ю_ ( r )

Examine       the       vicinity       of        r c :

| ю - ю_с | <^ | ю - ю_ |, | ю - ю₁1. Then Equation (42) allows for a further simplification:

⁵ r _[ ю^{2 -} ю^_ ( r ) ] a rV1 r - k y [ю^_ - ю^_ ( r ) ] ц r = 0.  (43)

Consider now the wave field structure near the other boundary of the SMS transparent region — the turning point r 1 . To do this, put |ю - ю₁|с|ю - ю_|,|ю - ю_с| in Equation (42). We obtain an equation in the azimuthally small-scale approximation

_{2       2} ю² - ю _ (г

5 24 r + ky      "М ^хr = 0.                  (48)

ю с - ю - ( r )

Using the linear expansion of the function ю^_ ( r ) near the point

2     2            2                    2 r - r r « ri,  ю- ю1( r )«-_ю1( ri )J ( r - ri ) = ю1-— , l1 we obtain an Airy equation д2 цг + X-3 (r - r) ц r = 0,                       (49)

Where X - 3 = k ²ю 2 Д (ю 2 -ю 2 ). Find solutions of (49):

V i r = a i Ai (-V ( ^{r - r} i ) ) + b i Bi (-V ( ^{r - r} i ) ) .     ⁽⁵⁰⁾

Near the resonance point r«rc we can expand toc(r) in a power series ю2 -Ю2(r)«-(ю2)(r-rc) = ю_r—rc. Then dif-lc ferential equation (43) becomes

As for the point r _ (the turning point in the one-dimensional case), it is still a singularity of the equation for SMS and in the curved case, but its meaning changes. In the vicinity of this point, where |ю - ю_|»|ю - ю_с|,|ю - ю^, Equation (35) allows for a further simplification:

-

⁵ r ^юс —p ⁵ r i' r - ky ( ^юс - ^ю1 ) 4 r = 0.

l _c

The solution of this equation has the form

Л ю-- ю2 (r )^      2   r;A д r  2    2 ( \ д r ^i r +    2 .2 ^i rд r ю - ю_ (r)        r V+ + 2)S

2      2

ю_ - ю8

2    Г ю - ю-

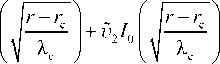
₂ ю² - ю2 ( r)

+ k    ₂ i ( ) 4 r = 0.

ю - ю_ ( r )

+

If we linearly expand to _ ( r ) near the point r ^ r _, Equation (51) can be transformed into

where it is denoted X J = k ^_ 1 ^c _ ¹ .

c y c_{ω c} 2

Given | r - r_c| <^X_c the solution of (45) has the same logarithmic singularity as in (23):

r - r

—

^д 24 r

( r - r_ ) 2

⁵ r ^Ui r

( r - r_ ) 2

V i r = ⁰

Here it is denoted

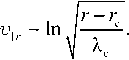
- i _ 2   v_A    Г ю - - ю^_

^{X -} =    2.2   2   2

r ^_A + 4 [ ю - - ю_с

The field-aligned and azimuthal components of the displacement have a pole singularity:

The general solution of (52) has the form

V i г = ( r - r - ) ^x

λ

1φc r - r

λ

1y          c r - r

x

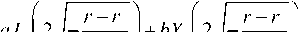
— J ^{+ b} Y _ ^²^-J

Sets of electric and magnetic fields have the form

E i r ~ B o — , E i y~ B o ln_A r - c , E , = 0, ^{r -} r c             V X c

B i r = B i y = 0, В 1Ф    B ^л' .

r - r_c

where J 2 ( z ), Y 2 ( z ) are second-order Bessel functions; a , b are arbitrary constants.

If r → r ,

Чг ~ ^а ( r - r_ ) + b

i r - r_ |    r - r_, П

---1--In n 2nX- ( v 2X-

. (54)

Thus, as the point r _ is approached the wave amplitude in the radial displacement component tends to a finite value. In the azimuthal component, the wave has, however, a logarithmic singularity

b 1 и -r .п uv--ln.--l-

¹ y   2п1 - ( V 21 -     2 J

The azimuthal and field-aligned components of electric

and magnetic fields take the form

E 1 r    B 0

b

2πλ

-

ln

2λ

—

—

π

2  ,

E 1 y

B

r — r

2πλ

■

ln

r — r

2λ

—

π

2  ,

E 1φ

= 0, B_A = B_A = 0, 1 r 1 y

B 1φ

B

b

2πλ

-

ln

2λ

—

—

π

.

Thus, if in the one-dimensional model the point r _ represents a reflecting point, in the curved model it is a point of the secondary (logarithmic) resonance. There is no analogue of this point in the one-dimensional model.

4. DISCUSSION

Compare results of the analysis of the cylinder model with those of the one-dimensional model discussed in Section 2 and with those of the dipole model studied in [Klimushkin, 1997; Klimushkin, 1998; Klimushkin et al., 2004] .

First, examine the Alfvén mode. As we saw in Section 2, in the one-dimensional case the Alfvén mode unlike SMS has no reflecting surface. Since the difference to 2 — ю² is proportional to the plasma pressure, in the cylinder model, but with a cold plasma, the Alfvén mode has no reflecting surface either. Thus, for the Alfvén mode the reflecting surface exists only in the finite pressure plasma with curved field lines. The resonant singularity is logarithmic as in the one-dimensional model, but the phase jumps by π/2, not by π as in the one-dimensional model. All these results check well with the results obtained in the dipole model of the magnetosphere, which takes into account inhomogeneous plasma and magnetic field along field lines [Klimushkin, 1997; Klimushkin, 1998; Klimushkin et al., 2004] .

The situation with SMS is somewhat different. In the one-dimensional case, the SMS reflecting surface was determined by ω = ω_( r ) and was located more to the right of the SMS resonant surface. In this case, as the azimuthal wave vector component k y increased, the SMS transparent region narrowed. In the cylinder case, the SMS reflecting surface was defined by ω = ω 1 ( r ). In this case, it is located more to the left of the SMS resonant surface. The difference between the SMS reflecting frequency and the respective resonant frequency is determined only by plasma and magnetic field parameters and does not depend on k y . Thus, the SMS transparent region in the cylinder model is much wider than in the one-dimensional model. This result agrees with the results of

the dipole model [Klimushkin, 1997; Klimushkin, 1998] .

The behavior of the resonant singularity in SMS in the one-dimensional and cylinder models is the same. In this case, the dipole model gives different results [Klimushkin, 1997; Klimushkin, 1998] , which is most likely to be its artifact. Indeed, let us turn again to Equation (42) for SMS. As already noted, the difference between ω c and ω_ in the azimuthally small-scale limit tends to zero. If we also neglect the differences between ω c and ω s , in the azimuthally small-scale limit the second term of this equation seems to be ignored as well. Then it takes the form

₂ to² — to 2 ( r)

d r d r 4 r — k 2 1Д4 ^ r = 0, (56) to — to_c ( r )

which coincides with the equation for SMS obtained by the dipole model in [Klimushkin, 1997; Klimushkin, 1998] . Obviously, the resonant singularity in Equation (55) has the form ~ ( ^r — r ) In ( r — r ) which differs from the correct result of (46) ц_г - ln ( r — r _c) . In addition, Equation (56) does not contain the secondary (logarithmic) resonance. Thus, we can conclude that the methods of studying azimuthally small-scale waves in the dipole model used in [Klimushkin, 1997; Klimushkin, 1998] are too crude to examine the behavior of SMS near the resonant surface, although they are quite suitable for studying the mode near the reflecting surface.

It should be noted that there are two questions concerning the subject matter of this work, which we did not address in this paper. The first of them is the ballooning instability whose development requires curved field lines and finite pressure plasma [Burdo et al., 2000; Agapitov et al., 2006; Liu, 1997; Bhattacharjee et al., 1998; Golovchanskaya et al., 2006] . This instability occurs in the SMS branch of oscillations during a sharp decrease in pressure with distance from Earth [Cher-emnykh, Parnowski, 2004; Mazur et al., 2012; Rubtsov et al., 2018b] . In this paper, we treat modes resistant to ballooning perturbations. In addition, in a collisionless plasma (plasma of Earth’s magnetosphere) the correct consideration of the finite pressure is possible only within the framework of kinetics when in the plasma there may exist ULF modes that do not occur in MHD, such as drift-compressional and mirror modes [Mikhai-lovskii, Fridman, 1966; Hasegawa, 1969; Rosenbluth, 1981] . In an inhomogeneous plasma, these modes are coupled with the Alfvén ones [Chen, Hasegawa, 1991] . This coupling has been studied using the cylinder model in [Pokhotelov et al., 1985; Woch et al., 1988; Klimush-kin et al., 2012] ; using a more realistic dipole model, in [Mager, Klimushkin, 2017].

CONCLUSION

The analysis of the cylinder model for one-dimen-sionally inhomogeneous finite pressure plasma with curved field lines enables us to do the following.

1. To derive an ordinary differential equation describing the transverse structure of Alfvén, FMS, and SMS modes. Using the WKB approximation, we have determined transparent regions of these modes.

• 2.    To examine singularities on magnetic shells of Alfvén and SMS resonances in terms of field line curvature and finite pressure. In the one-dimensional case, the Alfvén wave is an isolated resonant peak, and in the curved geometry the solution near the resonance point is oscillatory, whereas the behavior of the resonant singularity of SMS in the one-dimensional and cylinder model is the same. The behavior of the SMS resonant singularity in the cylinder model differs from that in the dipole model in [Klimushkin, 1997; Klimushkin, 1998] .

• 3.    To show that the SMS behavior near the reflecting surface ω = ω 1 ( r ) in the cylinder model coincides with the behavior in the dipole model. As for the turning point in the one-dimensional case ω=ω_( r ), in terms of field line curvature it becomes a point of the secondary (logarithmic) resonance for SMS.

The work was performed with budgetary funding of Basic Research program II.12. We are grateful to P.N. Mager for valuable comments and suggestions.