Пространственно-спектральный анализ бинарных дифракционных оптических элементов, кодированных на основе комплексного-сопряженного дополнения

Дифракционная оптика является универсальным средством формирования в заданной области пространства практически любого распределения комплексной амплитуды [1-3].

Однако современные технологии изготовления дифракционных оптических элементов (ДОЭ) хорошо отработаны и обеспечивают высокую точность только при бинарной структуре рельефа.

Известно множество методов бинарного кодирования комплексной функции пропускания [4-8]. Наиболее быстрыми по времени расчета являются неитерационные методы, в частности, методы цифровой голографии [4, 5], их модификации и обобщения [1-3, 8].

Одним из наиболее простых методов бинарного кодирования непрерывной фазовой функции является использование комплексно-сопряженного дополнения [9-14]. В этом случае фактически используется суперпозиция рассеивающего и собирающего оптических элементов, которые являются комплексно-сопряженными по отношению друг к другу.

В данной работе проводится исследование пространственного спектра кодированных элементов и анализ формирования дополнительных дифракционных порядков.

1. АНАЛИЗ

ПРОСТРАНСТВЕННОГО СПЕКТРА

Рассмотрим фазовую комплексную функцию пропускания в произвольной системе координат

(^ n):

т ( ^ n) = exp [- iф ( ^ n)].     (1)

Дополнение этой функции комплексно-сопряженным слагаемым:

т a ( ^ , n ) = 1 { exp [ i Ф ( 5 , n ) ] + exp [- i Ф ( ^ , n ) ] } =

2                                    (2)

= cos ^Ф ( ^ , n ) ]

позволяет выполнить простое бинарное кодирование на основе метода киноформа [1, 2], игнорирующего амплитудную функцию:

^т ь ( ^,n ) = ^ex P| i П ( 1-sgn { cos[^ф ( ^,n ) ] } ) . (3)

Игнорирование амплитудной зависимости позволяет в некоторых случаях, например при генерации мод лазерного излучения [15, 16], достичь эффективности 70-80% при погрешности около 15%. Высокая эффективность в данном случае обеспечивается за счет изначально бинарной фазовой структуры кодируемого поля. В общем случае теоретически дифракционная эффективность бинарного фазового элемента в полезном порядке не превышает 40,5% [1, 2].

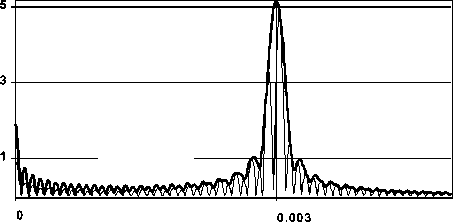
На рис. 1 показано сравнение пространственных спектров для радиальных функций

a)

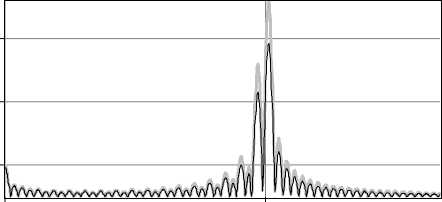
Рис. 1. Модули пространственных спектров:

0                                       0.003

б)

(а) для аксикона (толстая линия) и радиального косинуса (тонкая линия)

и (б) для бинарного аксикона (толстая серая линия) и радиального косинуса (тонкая линия)

т ax ( r ) = exp ( — ik a 0 r ) (дифракционный акси-кон), т _cax ( r ) = cos ( k a 0 r ) (радиальный косинус) ч Т.п 1 и ^т bax ( ^r ) = exp 1 i - { 1 ^— sgn L ^cos ( ^{k a} 0 ^r ) J } Г (бинарный а^ксикон), где k = 2п/Х , X = 0,000532 мм , a₀ = 0,003 , радиус апертуры R =3 мм.

Как видно из рис. 1, бинарный аксикон и радиальный косинус имеют очень похожие пространственные спектры. Чтобы объяснить расщепление спектрального максимума на пространственной частоте a₀ , проведем анализ спектра для входного поля A 0 ( r ) = cos( k a₀ r ) , ограниченного радиусом R . Его пространственный спектр без масштабного (нормирующего) множителя равен

R

S (о) = J cos( k a₀ r ) J ₀( k a r ) rdr .    (4)

На нулевой частоте значение S(0) вычисляется точно:

R

S (0) = J cos( k a₀ r ) rdr =

_ R sin( k a₀ R ) cos( k a₀ R )     1

k a₀          ( k a₀) ²      ( k a₀) ^{2 . (5)}

В выражении (5), как правило, преобладает первое слагаемое, поэтому его максимум по модулю будет достигаться при sin( k a ₀ R ) = —1 (при sin( k a ₀ R ) = 1 значение будет чуть меньше). В нулевом порядке энергия будет отсутствовать S(0)=0 при условии sin( k a ₀ R ) = 0 и cos( k a ₀ R ) = 1 ( при cos( k a ₀ R ) = — 1 значение мало, но не равно нулю). Для достижения абсолютного нуля нужно использовать равенство:

a₀ R = n X ,              (6)

где n – целое число.

Для оценки выражения (4) в общем случае учтем поведение функции Бесселя. Можно убедиться, что основной вклад даёт область вблизи верхнего предела. Поэтому, если радиус R достаточно большой, а частота s не очень мала по сравнению с a0, то функцию Бесселя можно заменить её асимптотическим приближением.

Используя приближение

J ₀( x )» 72 / (п x ) • cos( x — п /4)

и преобразование произведения косинусов к сумме, получим:

S (a) “ -/== ( S j (a) + S - (a) ) ,

V 2п k a

R

S 1 (a) = J cos ( kr (a₀ + о) — п / 4 ) 4r^r ,    (7)

R

S ₂ (a) = J cos ( kr (a₀ — a) + п /4 ) 4rdr .

Строго говоря, вблизи нижнего предела приближение функции Бесселя неприменимо, но вклад этой области мал. Оба интеграла не вычисляются точно, но интегрированием по частям можно найти их приближённое значение:

VR sin (kR(a0 + a) — п /4) о, (a) ~                                       , k (a0 + a)

S - (a)

RRL sin ( kR (a ₀ — a) + п /4 )

k (a ₀ — a)

Вблизи a = a₀ приближение для S ₂ (a) неприменимо, но оно показывает, что в этой области S ₂ (a) явно больше S Ja) и, поэтому можно ограничиться рассмотрением только его.

Непосредственно в точке a = a₀ значение вычисляется по (7):

R

S ₂(a₀) = J cos ( п /4 ) V rdr = (V-/3) R ^3/2 , (9)

однако численный расчёт интеграла (4) показывает, что это не есть максимум (рис. 1).

В окрестности с = а₀ можно качественно представить вид функции 5 *2 (с) при помощи следующих рассуждений. Подынтегральная функция в (7) на правом конце отрезка равна V R cos ( kR( а ₀ -с ) + п /4 ) . Благодаря низкой частоте лепестки достаточно широкие, и основной вклад вносит самый правый лепесток. Рассмотрим значения косинуса на правом конце отрезка интегрирования [0, R ]:

ления интеграла надо сделать удобное приближение косинуса. Его максимум, равный 1, достигается при r = r max = п R /45 . Хорошим приближением является разложение косинуса в ряд Тейлора с центром в этой точке, что даст:

Г п 5 Г 1 , cos---» 1

к4 R J

-

52      , V

Т72 (r - rmax ) . (11) 2R

Подставив это приближение в (7), получим

1, при с=а₀ + п /(4 kR ),

cos [ kR (а₀-с)+п/4 ] = <0, при с=а₀

-п /(4 kR ), (10)

-1, при с=а₀ - 3п /(4 kR ).

s Гс=a +—1=R/2 •

2 (       kRJ

2(1-п2/32)+—--

(3            10 7 J

Отсюда можно утверждать следующее: максимум S 2 (с) будет в точке с = а₀ + п / (4 kR ) ; минимум (отрицательный максимум) в точке с = а₀ - 3п / (4 kR ) ; переход через нуль между а₀ - 3п / (4 kR ) и а₀ - п / (4 kR ) . То есть, имеет место расщепление предполагавшегося максимума с = а₀ , причём оно несимметричное - смещение максимума в три раза меньше, чем смещение минимума. Правда, наше упрощённое рассуждение не даёт возможности предсказать высоту пиков, кроме того факта, что положительный максимум будет выше отрицательного - его лепесток при одинаковой высоте имеет меньшую длину из-за того, что частота больше.

Сравнение с результатами численного интегрирования по (4) показывает достаточную степень согласия с нашими предсказаниями (рис. 1б): правый пик больше левого; соотношение смещений пиков (в три раза) совпало с предсказанным: Ас lc = 0,003 - 0,00291 = 0,00009 (левый) и Ас rc = 0,00303 - 0,003 = 0,00003 (правый). Однако сами смещения оказались на 36% больше предсказанных теоретически, что связано с приближенностью расчетов.

Замена функции Бесселя её приближением и игнорирование слагаемого S 1 (с) не основной источник ошибки. Большей своей частью ошибка происходит от того, что благодаря наличию возрастающего множителя r максимум площади лепестка достигается не тогда, когда на правом конце косинус равен единице, а когда он немного меньше единицы на нисходящей ветви. Аналогичное рассуждение имеет место и для отрицательного максимума. Сделаем более точные оценки.

Используя (10), как некоторое начальное приближение, найдём площадь лепестков в явном виде. Сначала найдём максимум пространственного спектра. Исходя из (10), представим частоту в виде: с = а₀ + 5/ kR , п/4 < 5 < 3п/4 . Подынтегральная функция в (7) будет равна V r cos ( п/4 -5 r/R ) . От этой функции нет элементарной первообразной. Поэтому для вычис-

Эта величина достигает максимума при 5 = 7 п/20 , то есть максимум S ₂ (с) будет в точке с = а₀ + 7п /(20 kR ) . Его значение равно 0,634, что превышает значение спектра при с = а₀ (9) в 1,346 раза.

Подобным образом найдём и отрицательный (левый) максимум - представим частоту в виде: с = а₀ -5/ kR , 3п/4 < 5 < 5п/4 , а подынтегральная функция в (7) станет V r cos ( п/ 4 + 5 r/R ) . Здесь придётся использовать другое приближение косинуса. Он равен нулю при r = r ₀ = п R /45 и имеет минимум, равный -1 при r = 3 r ₀ . Имеем два лепестка, каждый из которых приближаем параболой: положительный лепесток (от нуля до r ₀ ) кривой

cos

п 5 r

--1--

4R

к

1 - , r0 7

,

(13а)

а отрицательный лепесток (от r ₀ до R ) кривой

cos

п 5 r

4R

«-1 +

r - 3 r0

2г к 2 r0

.

(13б)

Подставив в (7), получим

-

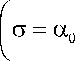
3/2 п

kR

= R ^3/2

•

-

к

22 853/2

5 125 8521

+ 7-+

6 5п 7 п J

Первое слагаемое в скобках меньше п ^3/2/ 228 ( 3п /4 ) 3/2 « 0,0068 , поэтому для упрощения его опустим. Оставшаяся величина достигает минимума при 5 = 21п/20 , то есть минимум S ₂(с) будет в точке с = а₀ -21п/(20 kR ) . Его значение равно -32/75=-0,427. Таким образом, максимум больше модуля минимума в 1,485 раза.

Новые скорректированные значения сохраняют соотношение смещений пиков в три раза и намного лучше согласуются с численными расчётами. Смещения всего на 3,2% меньше предсказанных теоретически.

Найденное выражение (14) позволяет также оценить положение нулевого значения спектра вблизи «0. Первое слагаемое в (14) в скобках меньше п"3/2/228 (п /4)3/2 « 0,035, поэтому им можно пренебречь. Решая получившееся уравнение, получим два корня 512 = 7п/16 (2,4 ± 1,4) . Меньший корень дает положение нуля при с = а0 — 7п / (16kR), что на 3,1% отличается от численных результатов ( с0 = 0,00296 ).

Как видно из рис. 1б, бинарный аксикон ока- зывается лишь немного эффективнее амплитудного косинусного элемента. Это связано с формированием дополнительных дифракционных порядков при использовании бинарного элемента.

В работе [17] было показано, что пропускаю- щую комплексную функцию оптического элемента с квантованной фазой можно представить в спектральный анализ бинарного аксикона и бинарной линзы на основе разложения комплексной функции пропускания такого элемента в ряд Фурье.

Для бинарного аксикона функция (3) является периодической с периодом T = 2п/ ( к а₀ ) , поэтому ее можно разложить в ряд Фурье. На отдельном периоде она записывается следующим образом:

1,0 < r < T/4,

т T ( Г ) = J — 1, T /4 < r < 3T /4,

1, 3T/4 < r < T.

Тогда коэффициенты в (16) для бинарного аксикона вычисляются по формуле:

T виде следующего разложения:

c p

dr =

ю

Тb (^ n)= Е сp exp [ipф (^П )] = p=—ю

ю

= с0 + Е сp cos [Рф К’п)].

p = 1

где Ф ( ^, п ) - исходная непрерывная фаза, а само разложение по косинусам означает совместное рассмотрение собирающего элемента (с отрицательным значением p ) и рассеивающего элемента (с положительным значением p ).

В частности, при кодировании аксикона с определенной частотой а₀ ряд (15) будет иметь следующий вид:

ю

Тbax ( r ) = с0 + Е сp cos (k“ pr ) ,   (16)

p = 1

т.е. бинарный аксикон представляет собой суперпозицию радиальных косинусов с кратными частотами а _p = а ₀ p .

В работах [11, 18] выполнен пространственно-

=

0, p — четное, p—1 4                       (18)

I 2 —, p — нечетное. пp

В частности, c1 = 4/п , c3 = — 4/(3п) , c5 = 4/(5п) . Квадрат первого коэффициента |c1| « 1,62 показывает энергетический выигрыш фазового бинарного аксикона по сравнению с амплитудным радиальным косинусом.

На рис. 2 показан пространственный спектр бинарного аксикона, демонстрирующий наличие кратных дифракционных порядков. Радиус ак-сикона выбран из условия (6) отсутствия энергии в нулевом порядке – R =3,5467. Основная пространственная частота аксикона равна а₀ = 0,003 . Из рис. 2 видно, что при кодировании вида (3) формируются только нечетные порядки p = 1,3,5,... , т.е. присутствует энергия на пространственных частотах а _p = а ₀ p .

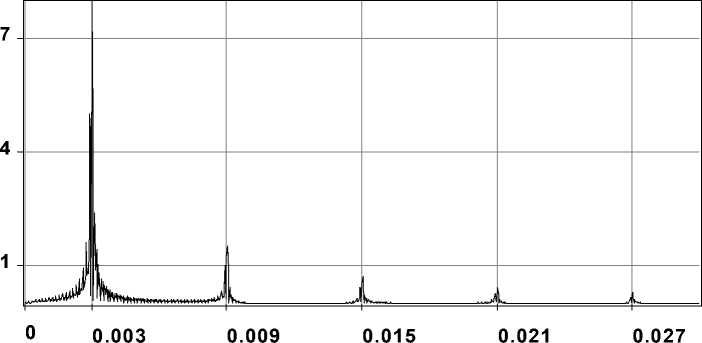
Рис. 2. Пространственный спектр бинарного аксикона с дифракционными порядками p = 1,3,5,... (нулевой порядок отсутствует в связи с выбором радиуса R по условию (6))

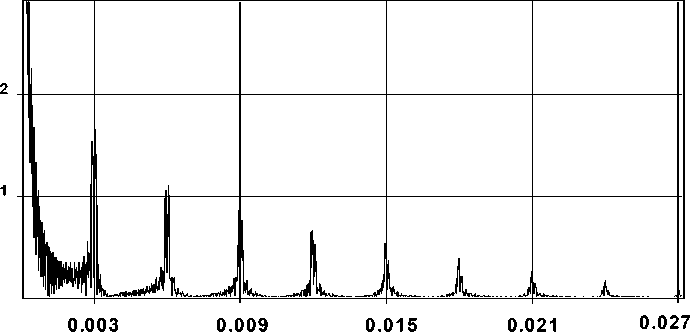
Рис. 3. Пространственный спектр предискаженного бинарного аксикона с дифракционными порядками p = 0,1,2,...

Способ кодирования можно изменить так, чтобы формировались другие порядки (рис. 3). Дополнительное предыскажение Ф ( ^, п ) позволяет управлять энергией, идущей в заданные дифракционные порядки [17]. Также менять коэффициенты в (16) можно при изменении относительного заполнения на периоде решетки [18].

Возникновение дополнительных дифракционных порядков при бинаризации соответствует формированию сложной картины, связанной с суперпозицией в (15) высокочастотных слагаемых. Для бинарного аксикона это набор радиальных косинусов (16) с более высокими кратными частотами, для бинарной линзы, соответственно, это набор линз с более короткими фокусными расстояниями.

Наиболее наглядно появление дополнительных дифракционных порядков при бинаризации фазы наблюдается для дифракционной линзы:

значениями 0 и p фазового элемента вычисляются из выражения:

sin [Фr (r)] = 0 >Фr(rn) = nn . (20)

В работе [19] исследовалось комплексное распределение, создаваемой на оптической оси радиально симметричным бинарным фазовым элементом, и было получено следующее выражение:

Fbn (0, z) = exP(ikz) x