Пространственно-временная динамика поперечного профиля оптического поля в лазере с отстройкой частоты

Образование структур в системах, демонстрирующих пространственно-временной хаос, является областью интенсивных исследований во многих областях науки. В нелинейной оптике подобные исследования мотивированы развитием общего понимания и описания появления периодических и квазиперио-дических структур, а также вихрей и пространственных солитонов в активных и пассивных нелинейных оптических системах. Данная работа посвящена исследованию процессов, происходящих в поперечном сечении световой волны, распространяющейся в широкоапертурном лазерном резонаторе.

В [1] было показано, что с увеличением числа Френеля в широкоапертурном резонаторе Nd-YAG лазера происходит переход от стационарны х поперечных картин к периодическим, квазипериодиче-ским и хаотическим картинам. Аналогичная картина получена в [2] для электроразрядного СО 2 лазера, работающего на одной продольной моде. В широкоапертурном лазере (при числах Френеля, больших 30) почти постоянная интенсивность становится промо-дулирована в пространстве периодической структурой и слабо промодулирована по времени с частотой ~150 кГц, которая зависит от величины отстройки моды от центра линии перехода. С увеличением числа Френеля, отстройки или накачки картина становилась сильно нерегулярной с полной потерей пространственной и временной корреляции. В [3] впервые показано, что наблюдаемые эффекты могут быть качественно объяснены на основе простой системы уравнений Максвелла-Блоха с отстроенной продольной частотой, которая описывает рождение бегущих периодических волн в результате биф урка-ции Андронова-Хопфа.

В настоящей работе на основе численного решения распределённой системы уравнений Максв елла-Блоха с адиабатически исключённой поляризацией исследована пространственно-временная динамик а поперечной структуры оптического поля в широкоапертурных лазерах.

Основные уравнения.

Автомодельные решения в виде бегущей волны

В качестве исходной рассмотрим сист ему уравнений Максвелла-Блоха с адиабатически исключённой поляризацией:

dE  d2E v Г N i — EI dt    dx2   2 (1+ A0

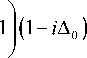
— = N -Tv[l + J

un I                 2

dt            ^   1 + Ao

.

Система уравнений (1) описывает пространственно-временную динамику лазера в предположении, что поляризация мгновенно следует за изменениями оптического поля. Такая модель в литературе часто называется ст андартным адиабатическим исключением поляризации. Предполагается также, что генерация происходит на одной продольной моде резонатора Фабри-Перо. Здесь E – медленно меняющаяся амплитуда поля в широкоапертурном лазере в одномерном (планарном) приближении, обезразмеренная на величину E s , E s – амплитуда поля насыщения в активной среде, N — g / g t ; g , g_t - коэффициенты усиления активной среды на центральной частоте лазерного перехода и потери, усреднённые по длин е резонатора; безразмерное время t и координата x связаны с размерными величинами t_d и x_d как t — t d / T i , x — x d ( 2 k / T , c ) ^1/2 , k - волновое число; c -скорость света; T i – время релаксации населённости уровней активной среды; v — cT i g t - коэффициент, определяющий отношение времени релаксации населённости активной среды ко времени жизни фотонов в резонаторе; A ₀ — ( ® ₀ - to ) T P - отстройка частоты генерации от центра линии усиления активной среды, обезразмеренная на полуширину линии усиления; T p – время релак сации поляризации; J ^— | E |2 , N un ^— g un / g t , g un ^- ненасыщенный ^коэф фициент усиления на частоте ω 0 .

Система уравнений (1) имеет два однородных состояния равновесия. Первое состояние равновесия соответствует отсутствию генерации:

• ( E = 0 ,N = N un ).

Второе состояние равновесия

• ( E = E st , N = N„ = 1 + А о² ) соответствует режиму стационарной генерации с интенсивностью J, = E ¹ = N - 1 -А ² st st un 0

В работах [4, 5] решение системы уравнений (1) искалось в виде бегущих с постоянной скоростью волн с использованием замены переменных ^ = t -в x , где w = 1 / в - скорость волны, распространяющейся в поперечном к оси резонатора направлении. В этой модели конечность апертуры резонатора не учитывается. Таким образом, исследовалась не полная распределённая система уравнений, а система обыкновенных дифференциальных уравнений (ОДУ), параметризованных при помощи в , при этом полагалось E = E '+ iE" . В дальнейшем эту систему будем называть автомодельной. В работе [4] проведён линейный анализ устойчивости режима стационарной генерации, который показал, что существует критическое значение в cr , при котором режим стационарной генерации становится неустойчивым. При в=в cr происходит бифуркация Анд-ронова-Хопфа, в результате чего рождается семейство периодических волн интенсивности малой амплитуды, параметризованных при помощи в •

Численное решение системы нелинейных ОДУ, проведённое в [5], показало, что все решения системы с н ачальными условиями вблизи положения равновесия (режи ма стационарной генерации) притягиваются к аттрактору - устойчивому двумерному эргодическому тору (рис. 1 а ). В работах [6, 7] показано, что исследуемая автомодельная система реализует не описанную в литератур е бифуркацию рождения тора из замкнутой особой кривой. Существование в фазовом пространстве системы аттрактора в виде устойчивого двумерного тора соответствует бегущим в поперечном направлении квазипериоди-ческим волнам для амплитуды оптического поля и периодическим волнам для интенсивности. При изменении управляющего параметра е=(в-в cr )/в cr наблюдается каскад бифуркаций удвоения периода тора, приводящий к режиму динамического хаоса (рис 1 а - г ). Для интенсивности наблюдается более простой механизм перехода к хаосу - через каскад бифуркаций удвоения периода цикла.

На рис. 2 приведена фазопараметрическая диаграмма, характерная для систем с каскадом бифуркаций удвоения периода. При построении на оси абсцисс откладывался управляющий параметр е, а на оси ординат - возможные значения максимумов интенсивности. На диаграмме хорошо видна область парам етров, в которой реализуется режим периодических волн интенсивности - одна ветвь, а также бифуркации удвоения периода, которым соответствует раздвоение ветвей.

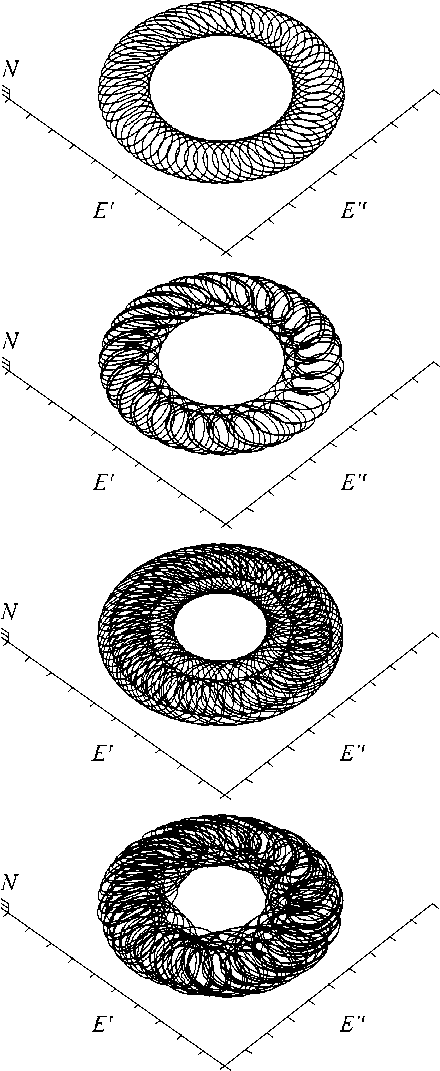
Рис. 1. Последовательность бифуркаций удвоения тора при А 0 = - 1, v = 4,4, N un = 5 :

£ = 0,01 (а), £ = 0,06 (б), £ = 0,076 (в), £ = 0,08 (г)

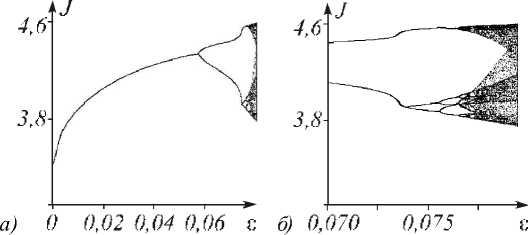
Рис. 2. Бифуркационная диаграмма (а) и её увеличенный фрагмент [5] (б)

Бесконечная последовательность удвоений приводит к фрактальной структуре странного аттрактора, что и определяет хаотическую динамику исследуемой системы.

Численное решение распределённой системы

Важным недостатком поиска решения уравнений (1) в виде волны, бегущей с постоянной скоростью, является предположение о бесконечно широкой лазерной апертуре. Известно, что подобные решения не всегда устойчивы при конечных размерах пространственной области, т.е. в данном случае при конечной ширине лазерной апертуры. Кроме того, в автомодельной системе в качеств е управляющего параметра выступает скорость во лн, которую не удаётся привязать к параметрам реальной лазерной системы. Также нет возможности менять данный параметр в эксперименте с целью управления свойствами лазерного излучения. Таким образом, автомодельная система может лишь помочь предсказать возможные режимы лазерной генерации .

В настоящей работе решается задача проверки устойчивости полученных ранее автомодельных решений на конечной апертуре с заданием периодических граничных условий E ( - L /2, t ) = E ( L /2, t ), N ( - L /2, t ) = N ( L / 2, t ), где L - длина расчётной области. Область изменения переменной x бралась L = 5 a , где a - ширина лазерного резонатора. Это позволяет практически исключить влияние граничных условий и физически соответствует открытому резонатору [8]. Уровень накачки брался однородным по всей ширине резонатора (рис. 3).

О               х

--1--*"1

а

L „

Рис. 3. Профиль накачки Nun( x)

Для численного решения уравнений (1) использовалась простая неявная разностная схема с четырёхточечным шаблоном на равномерной сетке, нелинейные слагаемые брались с предыд ущего временного слоя [9]. Значения безразмерных лазерных параметров брались a = 10, А ₀ = - 1, N_un = 5, как и в автомодельной задаче [5]. Параметр v использовался в качестве управляющего параметра.

Численные расчёты показали, что при небольших значениях управляющего параметра v любое начальное пространственное распределение поля E ( x , t = 0) с течением времени эволюционирует в стационарную пространственную структуру, показанную на рис. 4. При этом небольшая часть излучения выходит за границы открытого резонатора за счёт явления дифракции.

При увеличении управляющего параметра наблюдается рождение семейства автоволн (рис. 5). При этом если построить временную зависимость E ( x = 0, t ) и

N ( x = 0, t ) в центре резонатора, то мы получаем режимы генерации, качественно эквивалентные режимам автомодельной системы. В фазовом пространстве E '( x = 0, t ), E "( x = 0, t ), N ( x = 0, t ) существует аттрактор в виде устойчивого двумерного тора (рис. 6), предсказанный в автомодельной системе.

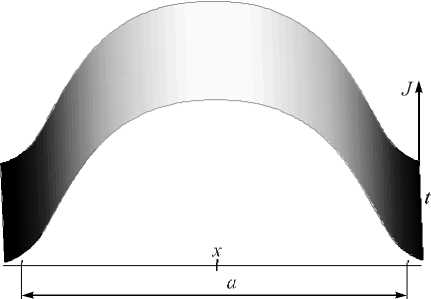
Рис. 4. Пространственно-временная динамика при v = 5

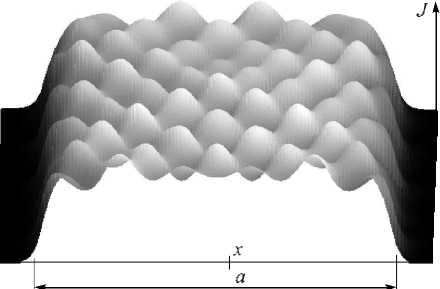
Рис. 5. Пространственно-временная динамика при v = 9,5

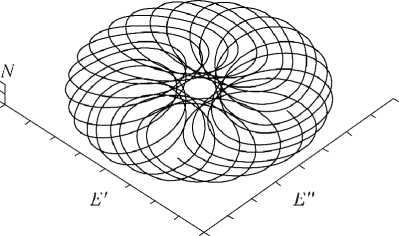
Рис. 6. Аттрактор в виде устойчивого двумерного тора при v = 9,5

На спектре зависимости действительной части комплексной амплитуд ы от времени хорошо видны две основные независимые частоты (рис. 7), свидетельствующие о движении фазовой траектории по двумерному тору, to - частота модуляции интенсивности и независимая частота Q .

При дальнейшем увеличении управляющего параметра в фазовом пространстве E'(x = 0, t), E"(x = 0, t), N(x = 0, t) наблюдается каскад бифуркаций удвоения периода двумерного тора и соответствующее усложне- ние пространственно-временных структур. При удвоении периода в спектре появляется субгармоника го /2 (рис. 8). Каскад бифуркаций удвоения приводит к переходу системы в режим пространственно-временного хаоса (рис. 9). О переходе системы в режим динамического хаоса свидетельствует спектральный состав зависимости интенсивности от времени (рис. 10).

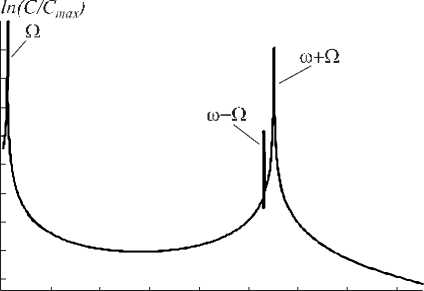
Рис. 7. Спектр колебаний E(x = 0,t) при v = 9,5 : C – мощность спектра, C_max – максимальное значение мощности

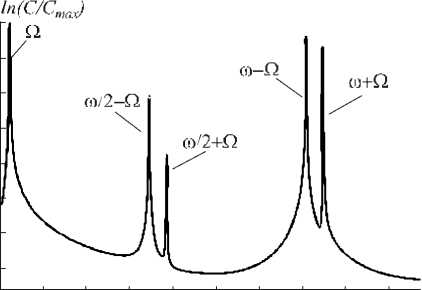
Рис. 8. Спектр колебаний E'(x = 0,t) при v = 11:

C – мощность спектра, Cmax – максимальное значение мощности

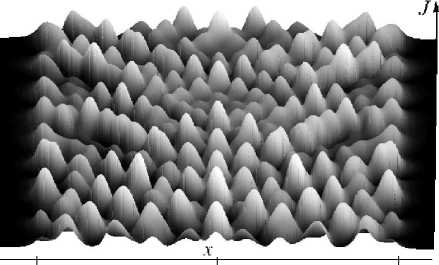
a

Рис. 9. Пространственно-временная динамика при v = 15

Заключение

В работах [4, 5] показано, что в лазерах с отстройкой частоты в предположении бесконечно широкой апертуры при некоторых значениях лазерных параметров возможно существование пространственно-временного профиля генерации в виде распро- страняющихся поперёк апертуры автоволн. В работе [5] детально исследованы бифуркации автоволн, показано существование в автомодельной системе аттрактора в виде устойчивого двумерного тора. В данной работе расчёты произведены с учётом конечности лазерной апертуры.

InfC'C^)

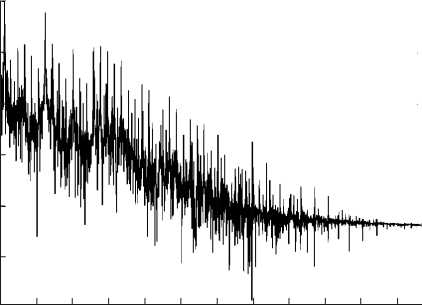
Рис. 10. Спектр колебаний J(x = 0,t) при v = 15 : С – мощность спектра,

Cmax – максимальное значение мощности

Найдены примеры значений параметров лазерной системы, при которых реализуется предсказанный автомодельной системой режим распространяющихся поперёк апертуры автоволн. Подтверждено существование в распределённой системе аттрактора в виде устойчивого двумерного тора. Найдены значения параметров, при которых в системе происходит скачкообразное качественное изменение пространственно-временной динамики (бифуркации), а также параметры, при которых наблюдается пространственно-временной хаос.

Однопараметрический анализ режимов генерации при фиксированных значениях других параметров, проведённый в настоящей работе, интересен с точки зрения выявления возможных режимов генерации и механизма перехода к хаосу в распределённой системе . На практике же маловероятно, что реальный лазер попадёт именно в ту область фиксированных параметров, для которой проводился однопараметрический бифуркационный анализ. В этой связи для дальнейших исследований практический интерес представляет построени е многопараметрических диаграмм режимов генерации.

Работа выполнена при частичной финансовой поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы, ГК №14.740.11.0703, Аналитической целевой программы «Развитие научного потенциала высшей школы» (2009-2010 гг.), проект 2.1.1/309.