Пространственно-временная структура альфвеновских резонансных возмущений, генерируемых поперечно-локализованной БМЗ-волной

Цель настоящей работы – определение условий формирования качественно различных пространственно-временных структур резонансных альфвенов-ских возмущений, генерируемых поперечно-локализованным БМЗ-возмущением.

Локализация БМЗ-возмущений в направлении поперек магнитного поля возможна, в частности, в областях вблизи минимума на поперечном профиле альфвеновской скорости. Такая неоднородность имеет место в магнитосфере Земли вблизи плазмо-паузы – магнитосферный БМЗ-волновод [Гульель-ми, 1972]. БМЗ-волны в этом волноводе являются стоячими не только в направлении поперек магнитного поля, но и вдоль него. В магнитосфере Земли образуются также поперечно-локализованные стоячие в направлении магнитного поля («глобальные ») моды в области вблизи магнитопаузы [Kivelson, Southwood, 1986] и поперечно-локализованные распространяющиеся вдоль магнитного поля моды в центральной части магнитосферного хвоста [Мартинес, Пилипенко, 2008]. Поперечно-локализованные моды могут также образовываться в магнитосферах активных областей Солнца.

Поперечно-локализованные БМЗ-моды являются резервуаром, который может сохранять длительное время энергию, полученную при быстрых внешних воздействиях. В магнитосфере, например, такими воздействиями могут быть изменения параметров солнечного ветра, приводящие к изменениям параметров как хвостовой части магнитосферы, так и ее части с замкнутыми силовыми линиями. На магнитной поверхности, где частота БМЗ-моды удовлетворяет локальному дисперсионному соотношению, имеет место резонансное поглощение БМЗ-волны – она частично трансформируется в альфвеновскую волну. Альфвеновская волна локализована в направлении поперек неоднородности альфвеновской скорости в слое, ширину которого можно считать малой по сравнению с поперечной длиной волны БМЗ-моды и масштабом неоднородности. Ширина резонансного слоя определяется такими незначительными факторами расстройки резонанса, как образование мелкомасштабных альфвеновских волн (кинетических и инерционных [Chen, Hasegawa, 1974; Swanson, 1975]), мелкомасштабное поглощение альф-веновского возмущения (столкновительное или бесстолкновительное поглощение [Ionson, 1978]) и затухание БМЗ-моды, порождающей резонансное возмущение.

При последовательном решении спектральной задачи без учета резонансного поглощения поперечно-локализованным модам соответствует дискретный спектр действительных частот, который при учете резонансного поглощения заменяется полосами непрерывного спектра. При введении комплексных частот поперечно-локализованные моды описываются как «квазимоды», действительная часть частоты которых соответствует действительной частоте моды без учета резонансного поглощения, а мнимая часть представляет собой декремент затухания моды вследствие резонансного поглощения. Различные БМЗ-моды вызывают резонансные альфвеновские колебания на различных поверхностях; если интервалы между частотами мод не слишком малы, то резонансные слои, соответствующие различным БМЗ-модам, не перекрываются.

При начальном импульсном воздействии на область локализации БМЗ-моды, она, если пренебречь затуханием, сразу приобретает свою амплитуду. Альфвеновское резонансное возмущение имеет большое время насыщения – оно обратно пропорционально ширине резонансного слоя. Поэтому его возбуждением в начальный момент времени можно пренебречь и считать, что оно возбуждается только под воздействием внезапно включившейся БМЗ-моды.

Поскольку резонансное поглощение крупномасштабной волны в тонком слое, как показано в настоящей работе, определяется только свойствами этой волны и среды, то крупномасштабная волна в резонансном слое может описываться как не зависящий от резонансного возмущения драйвер, амплитуда которого может быть задана в виде экспоненциально убывающей от начального момента функции времени. Параметры этой функции определяются свойствами среды и крупномасштабной моды и для резонансного возмущения могут считаться произвольными. Аналитические решения резонансного уравнения с драйвером указанного вида используются для аналитического описания пространственных структур различных типов, образующихся в резонансном слое.

Сравнение наблюдаемых резонансных структур с их аналитическими моделями может использоваться как для определения характеристик различных процессов в космической плазме, таких как нагрев плазмы солнечной короны и образование потоков ускоренных частиц в ионосфере [Stefan, 1970; Southwood, 1974; Ionson, 1978; Stasiewicz, et al., 2000], так и для диагностики параметров плазмы.

• 2.    Уравнения для возмущения в резонансном слое

Будем использовать одномерно-неоднородную модель среды. Невозмущенное магнитное поле В 0 , плотность ρ 0 , давление Р 0 зависят только от координаты х . Магнитное поле прямое, ось z выбираем вдоль В ₀. Возмущение { В , v , n , P_t } представляем в виде монохроматической волны с временной огибающей, например, возмущение магнитного поля

B = b ( x , T ) exp ( i 6 ) + c . c .,

• 6 =-to t + k z z + k y y ,                             (1)

где c.c . - комплексно-сопряженная величина, d _T << to .

Альфвеновское резонансное возмущение образуется вблизи поверхности x=x0, на которой частота и волновое число БМЗ-моды удовлетворяют дисперсионному уравнению для альфвеновских волн to2 - kV (x0 ) = 0, где Va =---0     - альфвеновская скорость [Chen,

(4 nP o ) ^1/2

Hasegawa, 1974; Southwood, 1974].

Используя в качестве исходных линеаризованные уравнения одножидкостной МГД с давлением и полагая dx - A 1, dT - A;                               (2)

d z -d y -d t -A ⁰ ,                           (3)

где Δ – малый параметр, характеризующий ширину резонансного слоя (т. е. области, где локализовано резонансное возмущение), Δ<<1 для возмущения вида (1) в резонансном слое, можно записать уравнения [Dmitrienko, 2007]

d x P t ^{( 0 )} = 0;                                           (4)

d x B¹^- y B y ^{- 1} ,                      (5)

L a¹ в y -¹’/ в 0 ( x 0 ) =

- V^x 0 ) k z k y ( 4 П P t ⁽⁰⁾/ B 02 ( x 0 ) ) .

Здесь P_t ^{( 0 )} - полное давление в резонансном слое, а

L a =- k ²( ( d _xV_a ²)( x 0 ) ) ( x - x ₀) + 2 tod _T d₆ - альфвенов-ский оператор в резонансном слое. Он дает добавку из-за неоднородности и нестационарности в правую часть дисперсионного уравнения для альфвеновских волн. Верхние индексы означают порядок величины как степени Δ.

Предполагая масштаб неоднородности большим по сравнению с масштабом резонансного возмущения, для получения нестационарного резонансного уравнения, учитывающего дисперсию и бесстолкновительное поглощение альфвенов-ских волн, достаточно достроить оператор L ^{ˆ (} _a ¹⁾ по дисперсионному уравнению для монохроматических альфвеновских волн в однородной плазме. Для низкочастотных колебаний (ω/ω _i <<1) дисперсионное уравнение для альфвеновских волн имеет вид [Ахиезер и др . , 1974]:

to2 - V2 kz2(1 - KkУ) = 0, k = -p2 /

1 + i _ ^to .      #k, v ,

I to w

IV2 k, v _e

⁺ 4 ^P i

1/2

1 I T I p - =H I to i i mi)

1/2                 1/2

1 I T I I T I, Pi =— I — I  , v e =1 — I

^to i I m i )         I m e )

,

где w – плазменная дисперсионная функция

w ( z ) = e ^{z /2} erfc ( - iz )

[Aхиезер и др., 1974; Abramovitz, Stegan, 1970]. При to .,. Qc2 ™

— >>v имеем Re K = ——, при kz                               tope to

— << v имеем k z

I 2 3 21

Re K = - 1 p 2 + 4 p i I . В первом случае кинетическое дисперсионное альфвеновское уравнение совпадает с дисперсионным уравнением для случая двужидкостной холодной плазмы МГД [Swanson, 1975] и описывает инерционные альфвеновские волны. Во втором случае оно совпадает с дисперсионным уравнением альфвеновских волн для случая двужидкостной плазмы с конечным давлением (за исключением коэффициента 3/4) [Hasegawa, Chen, 1976] и описывает кинетические альфвеновские волны. Мнимая часть K описывает бесстолкновительное поглощение альфвеновских волн. Обозначим d = k z Re K ( x ₀), a = k 2 Im K ( x ₀ ) . Re K может быть положительным или отрицательным, Im K принимает только положительные значения. В силу условий (2), (3) k_x ~ A^{- 1} , а k y - A ⁰ мы заменяем k ^ на -d 2 x ; множитель i согласно (1) означает d₆ , так что K заменяем на KK = Re K + Im K d₆ . В результате оператор L ^{ˆ (} _a ¹⁾ заменяется на

L a = ^{2 tod} t ^d 6 ⁺ ( ^d x^va ( x 0 ) ) ^x

x(x-x0)d2z -va (x0)(d + aЭб)Э2x, а резонансное уравнение принимает вид

[ k z ( ( ^d x V a )^{( x} 0 ) ) ( ^{x x} 0 ^{) + 2 toд} T ^d 0

- ^d V 2 ( ^x 0 ) ^д x ^д x - aV a ² ( ^x 0 ) d x d x d_e J B * ^{- 1 )} / B 0 ( ^x 0 ) =

- v a ( x 0 ) k z k y ( 4 n P t ^{( 0 )} / B 0 ( x 0 ) ) .                    (6)

Можно убедиться в том, что в частном случае d =0 (6) совпадает с резонансным уравнением одножидкостной диссипативной МГД. В этом случае k ²

a = [ v + p] - z -, где µ – коэффициент резистивности и to

ν – коэффициент вязкости.

Таким образом, уравнение (6), при придании коэффициенту a соответствующего смысла, описывает либо дисперсионный резонанс с модельным образом учитываемым бесстолкновительным поглощением, либо дисперсионный резонанс со столкновительным изотропным поглощением. Возмущение в (4–6) считается мелкомасштабным, т. е. изменяющимся с масштабом порядка Δ или меньшим. Поэтому уравнение (4) означает, что возмущение P t ^{( 0 )} не имеет мелкомасштабного изменения; оно представляет собой крупномасштабную волну, генерирующую резонансное возмущение.

B I B 0 ( x 0 ) = H , [ 4 Л P I B 02 ( x 0 ) ] = ^ .           (7)

Имеем

H ( x , T , e ) = h ( x , t ) exp ( i e ) + c . c .,

Ф ( x , T , e ) = V ( x , t ) exp ( i e ) + c . c .

Предполагается, что направление оси x выбрано так, что ( d x U a ) ( ^x 0 ) = ^- |( d x U a ² ) ( ^x 0 )| . Тогда ⁽⁶⁾ принимает вид

[ ^{- 2 д} т ^д е + d ^д Xx ⁺ a ^^д е ^-

-(^dxUa2)(x0)|)x]Н^ = (ky IkzИ0), где dxU2 = k- dxU^, а вместо (5) мы имеем dxHo)=-(ky Ikz )deHy-1).(9)

Уравнение (8) с учетом (9) дает уравнение энергетического баланса в форме теto дт J eR + J Ir =-[Ql(T) + Qs(T)],

- to-to где eR = (Hy 11) 14п - плотность безразмерной энергии резонансного возмущения (кинетической и магнитной), lR =-aHy lidxd%Hy11 I4n - потери плотности энергии из-за поглощения, QL(T) и QS(T) – безразмерные потоки плотности энергии крупномасштабной волны в резонансный слой и мелкомасштабной волны от резонансной поверхности соответственно.

ql (T) = qL (теT)- qL (-те, T), qL = -V(0)H" I4n = (-V(0)h^* + c.c.) I4n;     (10)

Qs(T) = qS(те T)-qS (-те T), qs = dH (-1)dzd6 H (-1) I4n = y x y                                (ii)

= ( dih ( ^{-1 )} ‘ d h '. ' ) I c . c ) I4 n .

Для величин e_R , q_L , q_S черта сверху обозначает величину, усредненную по периоду.

Положим Ψ ⁽⁰⁾ = F 0 f (τ) и введем обозначения

2h^(x, t) kz I(F0ky ) = G(X, t), x|(dx Ua2)(x0 )| I2 = X,

(|( dx U a ²)( x 0 )| I2 ) ² d I2 = D ,

(|( dx U a ²) ( x 0 )| I2 ) ² a I2 = A;                      (12)

D + iA = DD .                                 (13)

Новый дисперсионный коэффициент D , так же как d , может быть положительным или отрицательным, новый коэффициент поглощения A , так же как a , принимает только положительные значения. В обозначениях (12)–(13) уравнение (8) принимает вид

[ - i д т - X + D d X д X ] G = f .                  (14)

• 3.    Решение резонансного уравнения с произвольным драйвером и формулы сшивки крупномасштабного возмущения

Мы будем использовать в качестве основы для решения (14) его решение при A =0, f =const= f₀ , д_т = 0. В таком случае имеем уравнение

[-X + (signD)|D|дxдx JG = 1,(15)

G ( X , D ) представляет собой стационарное дисперсионное решение уравнения (14).

Запишем G ( X , D ) в виде

G(X,D) = -n(signD)|D|W где ^ = (sign D) XI |d| 1/3, а W является решением уравнения

[д^д^-^J W = -П-1.(16)

Для области распространения (ξ<0) получаем при ^ ^ -те

1          _L-2|e| 2I3

W 0 - С0^ЙТТ^ех Р ± i T 1^1

IЯ ^{[ 3}

где C ₀ – не зависящий от ξ множитель. Это означает, что при (sign D ) X ^ -да.

1              2 lt|3I2

^{G -} С^T/Texp ± i T I^я

IЯ         ^{[ 3}

где C – не зависящий от ξ множитель. Решение (17)

описывает волны, распространяющиеся вдоль оси x, в зависимости от знака в показателе экспоненты, или в направлении к резонансной поверхности, или от нее. Знак в (17) должен быть выбран так, чтобы волна уносила энергию от резонансной поверхности (т. е. проекция q S на ось ξ должна быть отрицательной). Решение неоднородного уравнения (16), которое обеспечивает такую асимптотику G при ^ ^ -да и ограничено при ^ ^ да, может быть составлено из стандартных функций:

W (5) = Gi (5)- i (sign D) Ai (5), где Gi(ξ) – решение неоднородного уравнения (16), а Ai(ξ) – функция Эйри. Такое решение для дисперсионного резонансного альфвеновского уравнения было указано в [Hasegawa, Chen, 1976]. При ^^да имеем W(5) ~ Gi(5)~л"15"1 [Abramovitz, 1970].

Таким образом, решение уравнения (15) имеет вид

G (X, D ) =-n( sign D )| D   x x [ Gi (5)" i (sign D) Ai (5)].

Используя интегральные представления для Gi и Ai [Abramovitz, 1970], получаем интегральное представление для G :

ф = 3 Du + Xu . При X из области распространения

волны, определяемой условием - X / D >0, фаза ф имеет положительную критическую точку и с : и с =(– X / D ) ^1/2 , и с >0. Вводя переменную s = u / u c –1, перепишем Р в виде

„ . 2 „      _ 31 2   13 1 1.3

P — i — Xu + iDu 5 +— 5 — Au .

3 c c (      3 J 3

Вблизи критической точки имеем

1 2„     „323    1

P = i — Xu. + Du’s¹ — u³A — + 5 .

1 3 c c ) c 1 3 J

Масштабы изменения фазы и поглощательной части показателя экспоненты как функции s есть £ ф = (| D| u 3 )’ ^1/2 и L a ( u 3 A f ¹ соответственно. При L ф<< L a , т. е.

|X /| D | ^1/3| << (| D |/ A ) ^4/3 (22)

изменением поглощательной части показателя экспоненты вблизи критической точки и с можно пренебречь, т. е. при | s |<<1 положить

TO

G = i J exp

• I ¹ TA 3 . AZ i — Du + Xu

du .

2         32

P = i — Xu + iDus ₃ c        c

¹ Au ³ . 3 ^c

Асимптотика G при (sign D ) X ^-to записывается с использованием асимптотических разложений для функций Gi и Ai [Abramovitz, 1970]:

G |D| i п^1/2 X /| D | ^1/3| ^1/4x

Интеграл набирается вблизи критической точки (при s <<1), если в дополнение к условию (22) выполняется условие

I X /| D | ^1/3| >> 1.

x exp

I 2 ^1      Га|1/3|3/2   П isign(D)I — 3 l|X/|D | + 4

( sign D ) X ^-to .                        (18)

Выражение (18) представляет мелкомасштабные волны, их масштаб определяется параметром | D | ^1/3 . При D >0 (18) описывает инерционную альфвенов-скую волну, при D <0 – кинетическую альфвенов-скую волну.

Когда f( t)= 1, d _T = 0, A ^ 0, имеем из (14)

[ - X + D d _X d X ] G ( X , D ) = 1.              (19)

Легко видеть, что продолжение G ( X , D ) как функции D в область комплексных значений D с Re D >0 согласно формуле

TO

G = i J exp 0

• I ¹ A 3 . AZ i —Du + Xu

du

является решением (19).

При A ≠0 для вычисления асимптотики G при | X |→∞ достаточно применить интегрирование по частям. Получаем

G = - X ^{- 1} .                                (21)

Для дальнейшего исследования выделим в P фазу

Совместное выполнение условий (22), (23) возможно при | D |/ A >>1. В таком случае получаем, что интеграл в окрестностности точки и с дает вклад в G в виде мелкомасштабной поглощаемой волны G S :

G S = | d|     i л ^1/2| X /| D | ^1/3| ^1/4x

x exp

x exp

¹ _{3 D} ^A X / D ^1/3

x

isign( D ) | - Ц X /| D | ^1/3^^/2 + 4 j

Интеграл вблизи конца интегрирования и =0 дает (21). Добавляя (24) в правую часть (21), получаем G = – X ^–1 + G S . Как видим, при A ≠0 и не слишком больших X G = G S , причем при A →0 область применимости этого равенства расширяется, так что при A =0 получаем (18). При A ≠0, – X / D >0 и достаточно больших значениях X выполняется условие, обратное (22). В этом случае изменение P в окрестности критической точки определяется поглощательной частью P , так что влияние критической точки несущественно, и мы получаем (21).

С помощью (20) может быть легко решено уравнение (14). Полагая, что драйвер включается при τ=0: f (τ)=0 при τ<0 – используем преобразование

TO to

Лапласа. Обозначая G L = J e ^{- p T} Gd T , f_L = J e^{p T} fd т и 00

полагая G =0 при τ =0, мы получаем для G_L уравнение [ - ip - X + D )d X d X J G L = f_L . Очевидно, что

те

^GL = if t f exP

I 1'3,

1 1 3 Du + ( X + ip ) u

du .

Осуществляя обратное преобразование Лапласа, получаем

T

G = i f f ( T- u )exp

• I 1 л 3 .

i — Du + Xu

du .

Обозначим времена и длины, присутствующие в подынтегральном выражении в (25). Будем использовать τ D и τ A для дисперсионного времени и времени поглощения: τ D =| D | ^–1/3 и τ A = A ^–1/3 . Кроме того, драйвер может привносить свое время; обозначим его т f . Длина A_a : A_a = т_а * соответствует каждому времени τ _α .

Выясним теперь, как изменяется амплитуда БМЗ-моды вследствие генерации ею резонансного возмущения (25). Интегрирование (9) по X с учетом замены переменных (12) дает при τ≠0, X 0 >0 следующее условие сшивки БМЗ-моды в резонансном слое:

4. Пространственно-временные структуры альфвеновских резонансных возмущений

1/3

Мы видим из (25), что пока D т<< 1, т<<т f и |dd| т ² <<  X |, можно пренебречь в (25) неидеальными эффектами, а также положить f (τ)= f (0). Тогда мы получаем для начальной стадии эволюции нестационарное решение вида

G = - X f (o) + X f (o)exP( iX T )'

Легко видеть, что при A =0 нестационарное возмущение продолжает существовать достаточно далеко от резонансной поверхности при любых τ. Асимптотика G при | X |→∞ и любых τ может быть определена с помощью интегрирования по частям при условии, что f ( и ) – ограниченная функция и ее масштаб δ f ненулевой. Получаем

G = G i + G e ,                              (29)

^Gi = ^- yexP [ ^-Y^t ] ,

G_f = —exp i f— D T ³ + X T

E X ( 3

exp

-

- A T ³ 3

.

A h x ( t ) = lim ( h x ( X o ) - h x ( - X o ) ) =

X o ^те

ⁿ F o

k ²

[ d x U 2 ( x o ) ] ^-1 f ( T ). k z ²

Очевидно, что G_I описывает амплитуду вынужденных колебаний. G E описывает собственные колебания с пространственной огибающей, так как функция

Такой режим резонансного поглощения может классифицироваться как квазистационарный. Формулы сшивки для вязкорезистивного резонанса получались в стационарном случае в [Einaudy, Mok, 1985], в случае затухающих нормальных мод в [Ruderman, et al., 1995]; для нестационарного резонанса – в [Dmitrienko, 1999].

Скачку (26) соответствует поток плотности энергии БМЗ-моды в резонансный слой

Q l =-| F o f ( t)| ² k y |(dx U_o ²)( x o )|^{_ 1} /2.

Поскольку потери энергии БМЗ-модой пропорциональны ее энергии в данный момент времени, то поперечно-локализованная БМЗ-мода затухает вследствие генерации резонансного альфвеновского возмущения с неким постоянным декрементом.

Можно считать, что при импульсном внешнем воздействии на область локализации БМЗ-моды она сразу приобретает конечную амплитуду, и для драйвера, моделирующего временно поведение БМЗ-моды в резонансном слое, можно полагать f (t) = exp[-ут], т > o,

f ( t ) = o, T< o.                         (27)

Таким   образом,   в случае поперечно- локализованной крупномасштабной моды получаем

G _o = exp

i f- DT3 + X т

exp

^- A t ³

– нестационарное решение однородного уравнения (14). Собственные колебания имеют зависящий от времени дисперсионный сдвиг частоты ΔΩ D (τ): ΔΩ D (τ)= – D τ ² . Он дает увеличение частоты со временем, если D <0, и убывание, если D >0. Поглощение вызывает затухание возмущения; появляется поглощательный декремент Г А (τ):Г А (τ)= А τ ² . Таким образом, G сохраняет нестационарный характер далеко от резонансной поверхности до тех пор, пока собственные колебания не затухнут из-за поглощения.

Заметим, что (25) представляет собой суперпозицию собственных колебаний G ₀, создаваемых драйвером в различные моменты времени. Отметим также, что имеется поверхность Х = Х 0 (τ), Х 0 = – D τ ² , на которой дисперсионный сдвиг частоты компенсирует изменение частоты из-за неоднородности, поэтому частота нестационарных собственных колебаний G 0 равна 0 (соответствующее возмущение (1) имеет при этом частоту ω).

T

G = i exp [ -ут ] f exp

i 3 Du + iXu + у u

du . (28)

4.1. Дисперсионные альфвеновские резонансные возмущения ( A <DI)

Обозначим P показатель экспоненты в (28) и запишем его в виде

2                     1       1

P = i — Xu + iDu3 52 + — 53 — Au3 +yu +ysu , 3 c c (      3   ) 3           c c где, как и выше, s=u/uc–1, uc=(–X/D)1/2, причем предполагается –X/D>0 и uc>0. Критическая точка ис фа-

зы ф (как и выше, ф = 3 Du + Xu) представляет со- бой точку, в которой дисперсионный и неоднородный сдвиги частоты компенсируют друг друга и частота нестационарных собственных колебаний G0 равна 0. Точка ис находится на интервале интегрирования, если значение X таково, что выполняется неравенство 0<–X/D≤τ2.

Мы видим, что фаза ф и часть P , обусловленная не-стационарностью драйвера (γ и с +γs и с ), имеют масшта-

₃ \-1/2              \—1

бы изменения (по переменной s ) ( Du_c )     и ( у u c )

соответственно. Если A =0, а ( Du c ) ^1/2 >>γ, т. е. если точка X находится в области, где выполняется неравенство

|X |/| D |^1/3 >> [у/| D |^1/3] ,                           (31)

что точка ис не попадает на интервал интегрирования, т. е. –X/D>τ2. Таким образом, мы можем определить линию фронта X=XF(τ). За линией фронта G имеет вид мелкомасштабной волны G=GQS (33), а перед ней представляет собой суперпозицию собственных и вынужденных колебаний. Имеем XF(τ)=X0(τ). Скорость фронта, так же как поток плотности энергии qS (11), направлена от резонансной поверхности независимо от знака дисперсионного коэффициента. Скорость фронта совпадает со скоростью распространения собственных колебаний G0: VF= –Dτ. Направление фазовой скорости мелкомасштабной волны и скорости фронта совпадают, если D<0, и противоположны, если D>0. Структура возмущения вблизи линии фронта может быть описана аналитически. Запишем (28) в виде то наиболее быстро изменяется фаза ф; если точка X находится в области, где обратное (31) неравенство имеет место, то наиболее быстро изменяется часть P, обусловленная затуханием драйвера.

1. Рассмотрим сначала случай γ/| D | ^1/3 <<1. В этом случае в той области значений X , где выполняется условие | X |/| D | ^1/3 >>1, неравенство (31) также выполняется. Изменением поглощательной части P , если A ≠0, можно пренебречь в области (22). Если X таково, что точка и_с попадает на контур, то интегрируем (28) вблизи и с , полагая

P = i — Xu + iDus² — Au +Y u          (32)

3 ^{c c} 3 ^{c       c .}

G = iu c exp [ - ут ]

0                    т / u -1

J exp Pds + j exp Pds .

Используя вблизи и с для Р выражение (32), учитывая малость масштаба изменения фазы ( Du C >>  1) и обозначая

П = т / u c - 1 =

L ( n ) = exp

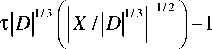
I X /I ^D l T n ,

”

- il ± —

Получаем квазистационарную мелкомасштабную волну

G = G qs ,

получаем

G f = ¹ g F G Qs , g F = 1 + erf ( LY              (34)

F ₂ F QS F

G qs = exp Y/I D ^1/3Q X /| D|^1/3|^1/2 -t| D |^1/3)

^G S ^,

где G S - стационарная волна (24). При y =0 имеем G = G S . Квазистационарный характер G обусловлен тем, что основной вклад в (28) вносит окрестность критической точки и = и_с , в которой частота нестационарных собственных колебаний G ₀ равна 0. Согласно (33) G имеет мелкомасштабную пространственную структуру мелкомасштабной волны (24). Множитель

Эта формура описывает G не только на фронте, но везде, где квазистационарная волна доминирует над вынужденными и собственными колебаниями, т. е. на фронте и за фронтом.

Обозначим значение G на линии фронта G F 0 . Получаем

G f o ( t ) = | D | ^2 i n ^1/2 exp

I           \-1/2

1/3

x (| D|    t )

exp

- ² iD t ³

exp

Y / D ^1/3 Q| X /| D | ^1/3|‘^/2— t| D |^1/3 )

П i^sig^{n( D} )- X

exp

- A t 3

Из (34) следует, что время прохождения фронта Δτ F через фиксированную точку Х убывает, если мы удаляем Х от резонансной поверхности:

описывает убывание амплитуды волны, уходящей от резонансной поверхности, вследствие убывания амплитуды драйвера. Волна распространяется с той стороны от резонансной поверхности, где выполняется условие sign X = –sign D , так что инерционная волна распространяется в области X <0, а кинетическая – в области X >0.

Как было отмечено выше, достаточно далеко от резонансной поверхности G представляет собой суперпозицию вынужденных G I и собственных G E колебаний (29). С той стороны от резонансной поверхности, где распространяется мелкомасштабная волна, G имеет вид (29) при условии, что X таково,

Atf(X) = |D|    X/|D| 1/3|   ;, а ширина фронта ΔXF увеличивается со временем:

A X f ( t ) = 2| D |^1/3 (| D |^1/3 т)¹/².

2. Теперь рассмотрим случай γ>>| D | ^1/3 . В этом случае имеется область значений X , при которых выполняется условие, противоположное (31):

j X |/| D |^1/3<<  [ y /| D |^1/3]4 .                           (36)

В этом случае в окрестности точки ис фаза как функция s изменяется с масштабом (γuc)–1. Для X из этой области мы можем положить

2         1 3

P = i 3 Xuc - 3 Auc + Yuc + Yucs вблизи ис, что означает, что наличие критической точки в таком случае несущественно, и величина интеграла (28) определяется интегралами вблизи концов интервала интегрирования. При γτ >>1 вынужденными колебаниями можно пренебречь, так как подынтегральная функция сильно убывает к точке и=0. Полагая вблизи и= τ

dxGf =-i3|D|”1/3|X/|D| 1/3|1/2 Gf, d XGND = i T GND .

Таким образом, можно сделать вывод, что продольное электрическое поле возрастает по мере того, как резонансное возмущение движется от резонансной поверхности. Его амплитуда принимает максимальные значения на фронте квазистационарной волны ( E_F ) и в центре нестационарного пакета ( E_c ). Можно получить из (34), (37) можно получить, что Е F ∞ τ ^1/2 , E c ∞ τ.

P = i ( D T ² + X - i y ) ( u -T ) - 3 A T ³ ,

получаем при γτ>>1 для значений Х , удовлетворяю-ших неравенству (36),

= 1            1 G .

Y [(X - Xo(T))/ Y-i] 0'

Здесь, как и выше, X 0 (τ)= – D τ ² . Согласно (37) G представляет собой пакет распространяющихся собственных нестационарных колебаний (30) («нестационарный пакет»). Определим центр пакета Х с как поверхность, на которой имеется максимум | G |. Имеем X_c = X ₀(τ). Таким образом, пакет распространяется со скоростью фронта квазистационарной мелкомасштабной волны V_c = – D τ. Ширина пакета Δ X_p – величина постоянная, A X p ~ y, a max G | ~ 1/ Y , ^т- е при распространении пакета его форма не меняется. Частота колебаний в пакете является функцией X и τ, она изменяется линейно по области локализации пакета, а в выбранной точке, через которую проходит пакет, имеют место колебания переменной частоты. По мере перемещения пакет уходит из области, где выполняется (36), и переходит в область значений X , удовлетворяющих (31). В этой области структура возмущения определяется интегралом вблизи критической точки, так что пакет становится несимметричным, приобретая передний фронт.

3. Продольное электрическое поле дисперсионных альфвеновских волн, хорошо известное из аналитического стационарного решения, давно связывается с мелкомасштабной структурой потоков заряженных частиц, высыпающихся в ионосферу [Goertz, Boswell, 1979; Stasiewicz, et al., 2000]. Рассматривая поток плотности энергии (11) как безразмерный вектор Пойнтинга, т. е. полагая

4.2 . Поглощаемые альфвеновские резонансные возмущения ( A >>l D I)

Когда коэффициент поглощения много больше дисперсионного коэффициента, поведение (28) определяется действительной частью показателя экспоненты Р .

1/2

I Y 1

Обозначим т m = I A I . Действительная часть

P имеет минимум при u = τ m . Введем обозначение u = τ m (1+ w ). Запишем P в виде

9                <        1 А

² л„3    л„3 I 2 ¹ 3 1

P = — Aт„ - AT„ w +-w +

₃ m m      ₃

^{+ iX T} m ^{(1 +} w ) ⁺ 3 ^{iD T} m ^{(1 +} w ^{) 3} .

1. Если декремент затухания крупномасштабной моды достаточно мал, то условие γτ _m <<1 может

Y3      , быть выполнено. В таком случае имеем — << 1, так

A что наличием минимумума можно пренебречь, так как exp Pu=т = exp Pu=0. Изменением множителя

exp

i ¹ Du ³

на масштабе А ^–1.3 , на котором набира-

ется интеграл (28), можно также пренебречь. Таким образом, в случае γτ m <<1 получаем

G = ^exp [ ^- Y^T ] ^Gsa ,

те

G SA = i J exP

-

1 л 3          ,

— Au + iXu du

q_s =- c E z B y / ( ^{ю B} o^{2 /} k z. ) ^,

получаем для амплитуды продольного электрического поля

e,    " Bdi d h и)

z ck ^x y

или

при τ >> A ^–1/3 . Согласно (38), G имеет пространственную структуру стационарного решения G_A с D =0, а его амплитуда затухает вместе с амплитудой драйвера. Решение G A соответствует стационарному поглощаемому решению. Ширина области, где локализовано возмущение, и его пространственный масштаб являются величинами порядка A ^1/3 . При | X |/ A ^1/3 >>1 аналогично (21) получаем G = - exp [ -yt ] X ^{- 1} , а при I X l<< A ^-1/3 фазовой частью показателя можно пренебречь, так что имеем

G = i exp( -YT ) A ~^1/32 л 3 ^{- 7/6} Г г f ² 11 .

e z /

[Y 2 D ( ( dx u a ) ( x o)| ) ^{- 1} F o k_f )

I ^ckz X                     k z )

Согласно (34), (37) имеем

- i d x G .

I2          1

2. В случае y/ A ^1/3 >>1 имеем exp I 3 AT³ _m I >>  1, так

что наличие точки τ m может быть существенно. По-

ка τ < τ _m , точка u = τ _m не попадает на интервал интегрирования, так что следует рассмотреть только вклады интегралов вблизи концов интегрирования.

т

о ( A , т ) = j и ( A , т ) d т = 1 - exp

-

2 л з

3 A ^т .

Поскольку exp

3 A ₃ + у и убывает к 0 с масшта-

бом у 1, то вкладом нижнего предела при 1<

вблизи и= τ, когда τ<< τ

G = Gna , Gna

m^,

мы получаем

уXIу-i

G0

при 1<<τγ<<γτm. Когда τ ≥ τm, на интервале интегрирования имеется точка минимума u=τ_m.

Если X<<γ и D/A<<(γA^1/3)^–3/4, изменением фазы вблизи точки минимума можно пренебречь. Следова-21 тельно, мы имеем P = — Aт³- A3w²+ iXт„ + -iDт3. mm    m   m

Безразмерная скорость нагрева vh = V_h / юB₀²определяется скоростью поглощения плотности энергии l_R: vh = -l_R. Получаем

1                 7

Vh = — (Foky I kz )²u(A, т),

4п

ФI (B о2/8п) = ( Fo ky I kz )2 a( A, т).

Таким образом, в случае, когда возникают нестационарные собственные колебания, скорость нагрева не является постоянной. а временное поведение нагрева является нелинейным. Такие свойства нагрева, очевидно, обусловлены тем, что измельчение пространственной структуры приводит к ускорению поглощения возмущения.

Обозначая

3/4

( у 1

GAi(X, A, т) = iп у I a^ I  exp[-ут]х

X exp 3 YTm

exp [ ^{iX т}m ] exp 3 ^iD<

,

получаем из (28) G=GA 1(X, т) и G = 2 GA,(X, тm)

при τ–τm>>(γ/A^1/3)^–3/4и τ = τm соответственно. Ква-зистационарная мода (40) затухает как целое с декрементом драйвера, сохраняя пространственную структуру нестационарных собственных колебаний (39) при т=тm. Пространственный масштаб - т-m, т. е. он меньше, чем масштаб А^1/3в квазистационарном случае. Пространственная структура такого типа была обнаружена посредством численного расчета при изучении затухающих нормальных мод [Ruderman, et al., 1995]. В [Ruderman, et al., 1995] было сделано заключение, что амплитуда резонансного возмущения возрастает, когда параметр А^1/3/γ уменьшается. Рассмотрение резонансного возмущения как результата эволюции приводит к выводу, что амплитуда резонансного возмущения с у1 больше, чем амплитуда резонансного возмущения с у₂, причем амплитуда резонансного возмущения (40) весьма мала в силу того, что оно образуется тогда, когда драйвер сильно затухает.

3. Поглощаемые возмущения представляют интерес прежде всего в связи с нагревом плазмы в области их локализации, например в связи с интерпретацией нагрева солнечных арок. Нагрев стационарным резонансным возмущением изучался в [Ionson, 1978]. Скорость нагрева Vh в таком случае постоянна во времени, а нагрев Φ имеет вид линейной функции времени. В случае, когда возникают собственные колебания (39), временное поведение скорости нагрева определяется временным поведением поглощения собственных нестационарных колебаний G0. Обозначим

и(A, т) = AGо^ДG₀+ c.c. = 2Aт²exp

2 A т3

,

5. Заключение

На основе решения эволюционного резонансного уравнения, учитывающего дисперсию и поглощение альфвеновских волн, определен характер эволюции и аналитически описаны пространственные структуры резонансных альфвеновских возмущений, генерируемых поперечно-локализованной БМЗ-модой, возбуждаемой импульсным внешним воздействием на зону ее локализации.

Показано, что если дисперсионный временной масштаб меньше поглощательного, то в зависимости от соотношения дисперсионного времени и времени резонансного поглощения БМЗ-моды возможно образование в резонансном слое мелкомасштабных альфве-новских распространяющихся возмущений двух типов. В случае, когда дисперсионное время меньше времени резонансного поглощения БМЗ-моды, в резонансном слое образуется резонансное альфвеновское возмущение с частотой крупномасштабной волны, представляющее собой уходящую от резонансной поверхности мелкомасштабную волну с передним фронтом. Амплитуда этой волны экспоненциально убывает в направлении от фронта к резонансной поверхности. Фронт движется равноускоренно, перед фронтом возмущение представляет собой суперпозицию собственных колебаний переменной частоты и вынужденных монохроматических колебаний; фронт расплывается в пространстве.

В случае, когда время затухания драйвера много меньше дисперсионного времени, образуется нестационарное возмущение в виде симметричного относительно своего центра нерасплывающегося пакета собственных колебаний переменной частоты. Этот пакет уходит от резонансной поверхности со скоростью фронта квазимонохроматической волны.

В обоих случаях возмущения распространяются от резонансной поверхности в сторону увеличения локальной альфвеновской частоты при кинетической дисперсии и в противоположном направлении при инерционной.

Полученные аналитические описания пространственно-временных структур резонансных возмущений позволяют определить продольное электри-

ческое поле в каждой резонансной структуре, что представляет особый интерес в рамках концепции, связывающей продольное электрическое поле дисперсионных альфвеновских волн с мелкомасштабной структурой потоков заряженных частиц, высыпающихся в ионосферу. Показано, что амплитуда продольного электрического поля, имеющего пространственную структуру мелкомасштабной альф-веновской волны, принимает максимальные значения на фронте квазистационарной волны и в центре нестационарного пакета и возрастает по мере того как резонансное возмущение движется от резонансной поверхности.

Если временной масштаб поглощения альфвенов-ского возмущения меньше дисперсионного, то под действием поперечно-локализованной БМЗ-моды образуются нераспространяющиеся альфвеновские возмущения, локализованные вблизи резонансной поверхности. Показано, что такие возмущения также могут быть двух типов. В случае, когда время резонансного поглощения БМЗ-моды существенно больше времени поглощения альфвеновского возмущения, образуется резонансное возмущение, имеющее пространственную структуру монохроматического поглощаемого альфвеновского резонансного возмущения; амплитуда такого резонансного возмущения экспоненциально убывает вместе с амплитудой генерирующей его БМЗ-моды.

В случае, когда время затухания БМЗ-моды меньше времени поглощения альфвеновского возмущения, сначала возбуждаются собственные нестационарные измельчающиеся в пространстве альфвеновские колебания. Когда декремент затухания БМЗ-моды и увеличивающийся со временем декремент затухания собственных колебаний сравниваются по величине, измельчение пространственной структуры прекращается, и резонансное возмущение на стадии своего исчезновения затухает с декрементом драйвера, сохраняя постоянную пространственную структуру нестационарных колебаний в момент прекращения измельчения.

Интерес представляет производимый поглощаемыми резонансными возмущениями нагрев плазмы в области их локализации, например при интерпретации нагрева солнечных арок. Получены формулы, описывающие временное поведение скорости нагрева. Показано, что в случае, когда возникают нестационарные собственные альфвеновские колебания, скорость нагрева, в отличие от случая монохроматических колебаний постоянной амплитуды, не является постоянной, а временное поведение нагрева не является линейной функцией.