Пространственно-временные характеристики четырёхволнового преобразователя излучения в прозрачной среде с учётом электрострикции и эффекта Дюфура

Знание пространственно-временных характеристик четырёхволновых преобразователей излучения является необходимым условием использования их в системах адаптивной оптики, в системах обработки изображения [1]. В приближении заданного поля по волнам накачки линеаризация уравнений, описывающих четырёхволновое взаимодействие, позволяет при нахождении соответствия между комплексными амплитудами взаимодействующих волн широко использовать такие понятия классической оптики, как функция размытия точки и временной отклик [2, 3].

Пространственные, пространственно-временные характеристики достаточно подробно изучены для четырёхволновых преобразователей излучения в средах с керровской, тепловой, резонансной нелинейностями, на обратимых фотохромных материалах [2-4].

Ещё одним классом нелинейных сред, используемых для получения при четырёхволновом взаимодействии волны с обращённым волновым фронтом (ОВФ), являются многокомпонентные среды, в которых реализуются несколько механизмов нелинейности, например, термодиффузионный и электрострик-ционный [5, 6]. Анализ пространственных характеристик четырёхволнового преобразователя излучения в поглощающей нелинейной среде с учётом электрострикции, термодиффузии, эффекта Дюфура проводился в работе [7].

В настоящей работе анализируются пространственно-временные характеристики четырёхволнового преобразователя излучения в прозрачной среде с учётом электрострикции и эффекта Дюфура.

фура изменяет температуру, а значит, и показатель преломления среды.

В результате вырожденного четырёхволнового взаимодействия щ + щ - щ=щ генерируется объектная волна с комплексной амплитудой A ₄, распространяющаяся навстречу сигнальной волне.

Исходное скалярное волновое уравнение, описывающее четырёхволновое взаимодействие излучения в нелинейной среде, есть [2]

f V2 + k2 + 2k- — 8 T)(A + A = 0,(1)

(         n 0 d TУ ’ где 8T - изменение температуры, A = V Aj, k = ^n-, j=1

n ₀ - среднее значение показателя преломления.

Уравнение (1) дополняется системой балансных (материальных) уравнений для изменений концентрации и температуры [5 - 9]

— = D ₂V ² 8 C + YV ² 1 , d t ²²

c p vd T = D _nV ² 8 T + D ₁₂ V ² 8 C .

Здесь I = AA * , 8 C - изменение концентрации частиц, D 11 - коэффициент теплопроводности, D 22 - коэффициент диффузии, D ₁₂ - коэффициент Дюфура, у - коэффициент электрострикции, c p - удельная теплоёмкость вещества, v - плотность вещества.

Четырёхволновое взаимодействие излучения рассматривается при следующих условиях [4]:

• 1)    справедливо приближение заданного поля по волнам накачки | A 1, ₂|>>| A ₃ , ₄|;

• 2)    коэффициент отражения мал | A ₄|<<| A ₃|;

• 3)    учитывается интерференция первой волны накачки и сигнальной волны.

Интенсивность излучения, распространяющегося в нелинейной среде, можно записать следующим образом:

I = I о + A 1 A 3 + A ₁ A 3 .

Здесь 1 ₀ = A 1 A + A 2 A .

Тогда изменения температуры и концентрации можно представить в виде суммы быстро ( 8 T ₃₁, 8 C ₃₁) и медленно ( 8 T ₀, 8 C ₀) меняющихся в зависимости от координат составляющих:

8 T ( Г, t ) = 8 T o ( Г, t ) + 8 T 31 ( r, t ) ,

8 C ( Г, t ) = 8 C ₀ ( r, t ) + 8 C 31 ( Г, t ) .

Пусть волны накачки плоские:

A12 (r, t) = A^ (z, t) exp (-i—2 r), где k12 - волновые векторы волн накачки, r (р, z) -радиус-вектор, р (x, y) и z - поперечная и продоль- ная составляющие радиус-вектора.

Сигнальную и объектную волны разложим по плоским волнам:

^

A j ( r, t ) = J A j ( к j , z , t ) exp ( - i к j р - ik jz z ) d K j . -^

Здесь j = 3,4, A j - пространственный спектр j -й волны, K j и k_jz - поперечная и продольная составляющие волнового вектора k j .

Быстро меняющиеся составляющие температуры и концентрации разложим по гармоническим решёткам

^

8 T 31 ( r,t ) = J 8 7 3,1 ( к t , z , t ) exp ( - i к _т р ) d K _T ,

-^

^

8 C ₃₁ ( * , t ) = J 8 C ₃₁ ( к _C , z , t ) exp ( - i к _C р ) d K _C . -^

Здесь 8 T ₃₁, 8 C ₃₁ - пространственные спектры тепловой и концентрационной решёток, к _т , к _C - волновые векторы соответствующих решёток.

С учётом приближения медленно меняющихся амплитуд при квазиколлинеарном распространении взаимодействующих волн (k/k1,3z =

-

k/k 2,4 z = 1) урав-

^P ( ^z , t ) = i —^n j^{8 T} 0 ( z_p t ) d z 1 .

n ₀ d T ₀

Сделаем замену А ₄ ( z , t ) = A 4 ( z , t ) exp [ P ( z , t ) ] . Тогда уравнение, описывающее изменение пространственного спектра объектной волны, примет вид:

dA-4 (z, t) . k d n — .        \ ~ . \ д i дт 8T31 (кT , z, t) A20 (t)X dz      n0 dT

X exp [- P ( L , t ) ] exp [- i ( k 2 _z - k _{4 z} ) z ] = 0.

С учётом граничного условия A ‘ ( к ₄, z = L , t ) = 0 временная зависимость пространственного спектра объектной волны на передней грани нелинейного слоя есть

.A 4 ( ^к 4 , ^z = ⁰ , t ) = ^- i — ^n .A 20 ( t ) exp ^[- P ( ^L, t ) ] ^X n ₀ d T

L xJ8T31 (кT, z, t) exp[-i(k2z - k4z)z]dz.

Пространственный спектр объектной волны пол- ностью определяется пространственным спектром тепловой решётки.

Для определения пространственного спектра тепловой решётки воспользуемся материальными уравнениями (2)–(3). Вначале, используя уравнение (2), найдём изменение во времени пространственного спектра концентрационной решётки. Затем, подставив решение уравнения (2) в уравнение (3), найдём изменение во времени пространственного спектра тепловой решётки.

С учётом разложения тепловой и концентрационной решёток по гармоническим решёткам, решений нение (1) распадается на систему уравнений вида dA1,3    k dn

+ i8 TA 1 = 0, dz     n0 dT 0 1,3

для амплитуд волн накачки, пространственного спектра сигнальной волны уравнения (2)–(3) перепишутся следующим образом:

d A 4

k dn i n0 dT k dn i n0 dT

8 T o A = 0,

8 T A -

— 1

' i^k I n ⁸ T 31 A 2 exP [^- i ( ^k 2 z ^{- k} 4 z ) z ^] = ⁰ . n ₀ d T

Уравнения (4) записаны при условии, что

—*       —*

к T =к,

—*      —*       —*      —*

_C = к ₁ - к ₃ = к ₄

к 2 .

Решение первых трёх уравнений системы (4) есть

A ( z , t ) = A w ( t ) exp [- P ( z , t ) ] ,

A ( к ₃, z , t ) = A ₃₀ ( к ₃, t ) exp [- P ( z , t ) ] ,

A 2 ( z , t ) = A 20 ( t ) exp ^[- P ( L , t ) + P ( z , t ) ^] .

Здесь

A 10 ( t ) = A ( ^z = ⁰ , t ) ,

% ( к 3 , t ) = A ( к 3 , z = 0, t ) ,

.4 20 ( t ) = A ( z = L , t ) ,

d8 C₃₁ ( к _C , z , t )

d t

D 221 , 2 ^к c j^{8 C} 31 ^(к c , ^z , t )

-Y^[ ( k 1 z - k 3 z ) 2 + к 2]. А ю ( t ). 4 30 ( к 3 , t ) x              (6)

^X exp ^[- i ( ^k 1 z ^{- k} 3 z ) ^z ] ,

^{d8 T} 31 ^(к T , ^z , t ) _ D 11 ( _d_    2       /* л

I _    ^к t I ^{8 T} 31 ( ^к t , ^z , t ) ⁺

C p V ( d z      )

d t

+ D 1 ² 1 -к 2 j 8 C :₃ ,(к_с , z , t ) . c p V ( d z ²      J

При отсутствии потока частиц через грани нелинейного слоя, с учётом начального условия 8 ( ? ₃₁ ( к _C , z , t = 0 ) = 0 будем искать решение уравне-

ния (6) в виде ряда Фурье [10]:

^

⁸ C % 31 ( ^к C , ^z , t ) = ^ C m ( ^к C , t ) cos-^ ^z .             ⁽⁸⁾

m = 1                      ^L

Подставив (8) в уравнение (6), найдём коэффициенты ряда

² i ^{[( k} 1 z ^{- k} 3 z ) ^+К 3 1 C_m К_г , t = Y — Ц;---- ^] X ^{m ( C} , ) ^Y        ( k 1 z - k 3 z ) L

² i ^{[( k} 1 z ^k 3 z ) ^+К 2 ] D

⁸ 7 31 (^K t , ^z , t ) = ^-Y------7--^X

ⁿ ( ^k 1 z ^{- k} 3 z ) ^L      c p ^v

X

¹ - ( ^{- 1} ) m exp [~ i ( k 1 z ^- k 3 z ) ^L ]

1 -

( пm

V

X

l ( k 1 z - k 3 z ) L J

. Ks -r ^X Z siny ^z Z s = 1 ^L m = 1

1 - ( - 1 ) s ^{+ m} ₊ 1 - ( - 1 ) s

s + m

: - m

X

s — m

t.                I

X j exp 3 - D ₂₂ о              I

п m ।     ₂

— +К 2

L J     ^c

( t ^-t ) - ^X

{ 1 - ( - 1 ) m exp ^[— i ( k 1

X-----------------

1 -

( пm

■ 1 z ^k

I ²

n m I     2

— +К 2

L J

X

x^ 4 10 ( т ) x 4 ;0 ( К 3 , t ) d T .

Учитывая начальное условие 8 7 3 ₃₁ ( К _T , z , t = 0 ) = 0 и неизменность температуры на гранях нелинейного слоя ( 8 7 3 ₃₁ ( К _T , z = 0, t ) = 8 7 31 ( К _T , z = L , t ) = 0 ), явный вид пространственного спектра тепловой решётки будем искать, как и при нахождении пространственного спектра концентрационной решётки, в виде ряда Фурье [4, 10]:

l ( k 1 z - k 3 z ) L J

tt ‘

^X jj ^A 10 ( ^T ) ^A 3 0 ( ^K 3 , ^T ) ^X

X exp 3— D ¹¹ I c P ^v

X exp 3 — D 22

8 7 31 ( ^K t , ^z , t ) = Z T s ( ^K t , t ) ^sin 7 ^z . s = 1                     ^L

Подставив (10) в уравнение (7) и используя (8) – (9), найдём изменение во времени пространственного спектра тепловой решётки в виде:

n s I 2

-- +К 2

L ^J T

п m ।    2

— +К 2

L J

( t - 1 ') f X

( t '— t ) - d т dt '.

С учётом (11) выражение (5), описывающее временную зависимость пространственного спектра объектной волны на передней грани нелинейного слоя, примет вид

А ( К 4 , z = 0, t ) = . L. ( t ) exp [— P ( L , t ) ] X

,R             x ^{[( k} 1 z ^{- k} 3 z ^{) 2 +К} 3 ¹ 2 k d n

у(к, , t - 1 , t -t) = y- ------------5  -- x

( 4             )       ( k1 z - k3 z )3 L2 n 0dT t t'

X j j x ( К 4 , t — t ', t ' — t ) .4 10 ( T ) A 0 ( К 3 , т ) d T d t' 00

где

X ( K 4 , t — t', t '-t ) = y

^[( k 1 z ^— k 3 z ^{) 2 +К} 32 ] 2 k d n

D ₁₂

( k 1 z - k 3 z ) 3 L ^{2     n} 0^{d T} c p v

^ ^ zz s = 1 m = 1

s { 1 - ( - 1 ) s exp [- i ( k

1 —

( ns

' 2 z

I ²

X

X

{ 1 — ( ^{- 1} ) m exP ^[ i ( ^k 1 z ^{— k} 3 z ) ^L ] } [ 1 - ( - 1 )

1 -

( пm

l ( k 1 z — k 3 z ) L J

X exp J — D ¹¹ I c P ^v

s + m

s + m    л ( л s- - m

I ₊ ^{1 -} ( ^{- 1} )

s — m

IL ( k 2 z - k 4 z ) J

n m I ^{r r} \ 2

— +( к₄-к₂ ) X

L ^{J         4      21}

n s I    /R R X 2 Z /X

- J +^(К 4 ^—К 2 ) ⁽ t ^— t ) l exp

^— D 22

n m I _Zr

-^{J +(К} 4 ^—

К 2 ) 2 ( t '— t ) -.

Выражение (12) с учётом (13) устанавливает однозначную связь между временными зависимостями пространственных спектров взаимодействующих волн.

2. Обсуждение результатов

В качестве сигнальной волны рассмотрим волну от точечного источника, расположенного на передней грани нелинейного слоя ( A ₃₀ ( К ₃, t ) = 1).

Будем считать, что волны накачки распространяются строго вдоль оси Z ( К 1 = К ₂ = 0) и их амплиту-

ды не меняются во времени ( А 1, ₂₀ ( t ) = А 1, ₂₀).

После интегрирования по временным переменным правой части выражения (12) с учётом (13) в параксиальном приближении ( k _{34 z} = k — К 2 ₄ / (2 k )) получим:

dn (2 k)

A4 (К, z = 0, t) = Y--—

1 i n s f- К² L ^{X 1} -⁽- 1 ) exp I -25

. к2 , ,

^{1 1} !/< ⁴ 10 A 20 ^exp 4 k

л Лm f -K 2 L ^{1 -} ( ^{- 1} ) exp l ^- i 2^

^ ^

[-P (Lt)] xZZr

1 - ( - 1 ) s

s — m

s = 1 m = 1

m 1/1\ s + m ₊ ^{1 -(-1)}

s + m

s f 2n ks I2

1 — l К L J

c P ^v

D 11

■              229X f 2n km I

1 — l к L J

\ 2         "1 1

П s I 2

-- +К2

L ^J

X

г х 1 - exp

I

f   D 11

-

C V

L c p

+ κ2

A

t -

c p ν

- exp

D 11 c p ν

+κ ²

)t > >.

J

Здесь к = |К4| = |K3|

^J D 11

+ κ2

- c_p ν D ₂₂

+ κ2

exp

I

- D ₂₂

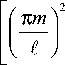
+ κ2

t г —

С течением времени пространственный спектр объектной волны выходит на установившееся значе-

ние, определяемое выражением:

-А ‘ ( к , z

= 0,t → ∞ ) = γ

d n ( 2 k ) ⁴    D 12

d T n 0 k⁴L ² D 11 D 22

×

[     К ² '

^х + 4ke

∞∞

A10 A;- exP [—P ( L ЖЕ 5 X s=1 m=1

×

Г 2 n ks ? [ ’ -1 К . J J

Г 2 n km У [ ’ -1 K 2 L J J

[/_ _A2     1 1 n s |        2 [17 J +KJ

1 - ( - 1 ) ^s exp

×

концентрационной и температурной решёток. Процессы теплопроводности, диффузии размывают решётки. На малых пространственных частотах доминирует электрострикционный механизм записи решёток, приводящий к увеличению модулей их пространственных спектров. На больших пространственных частотах увеличение модулей пространственных спектров решёток вследствие электрострикции компенсируется размытием решёток вследствие процессов теплопроводности, диффузии. Это объясняет характер изменения пространственного спектра объектной волны с ростом пространственной частоты.

×

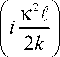
m ^Г . K2 L

^{1 -} ( ^{- 1} ) exP I ^- i 2^

×

×

1 - ( - 1 ) ^{s - m} ₊ 1 - ( - 1 ) ^{s + m} s - m s + m

Как следует из выражения (14), коэффициент

электрострикции не влияет на динамику пространственного спектра объектной волны.

Введём безразмерный параметр, характеризующий

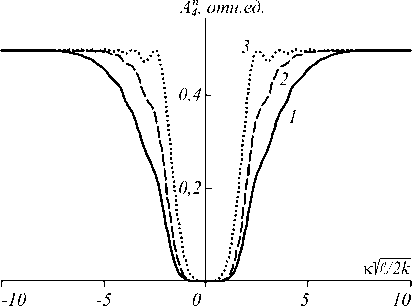
Рис. 1. Пространственные спектры объектной волны при b=2-10 - ⁵, 2kt=10 4 , t(D₂₂/1²)=10^-5 (1), 2^1^-⁵ (2), 1(T³ (3)

При фиксированной пространственной частоте модуль пространственного спектра объектной волны с течением времени возрастает, выходя на установившееся значение.

Введём время выхода модуля пространственного спектра на фиксированной частоте на установившееся значение ( ∆ t ), определяемое из условия:

нелинейную многокомпонентную среду b = c_p ν D ₂₂/ D ₁₁. В случае воды, в которой находятся наночастицы размером примерно 10^–8 м, параметр b =2·10^–5 [8].

На рис. 1 представлены модули нормированных пространственных спектров объектной волны

A 4 ⁿ

I a ,i Г 2 k t d n  D 12

I ⁴1 ^ n ₀ d T D 11 D 22

-и -и γ A 10 A 20

- 1

в различные моменты времени. При расчётах максимальные значения индексов суммирования s и m в выражении (14) определялись относительной ошибкой при нахождении модуля пространственного спектра (10^–3) и достигали значений 55 для высоких пространственных частот ( κ ).

С увеличением пространственной частоты наблюдается рост модуля пространственного спектра с последующим выходом на постоянный уровень, значение которого близко к 0,5.

С физической точки зрения увеличение модуля пространственного спектра обусловлено наличием электрострикционного слагаемого ( yV² I ^ yV 2 A 1 A ) в материальном уравнении для концентрации частиц (2). С уменьшением периода записываемой интерференционной решётки электрострикционное слагаемое растёт, а значит, увеличиваются амплитуды записываемых

|A'4(K, t = A t )| = 2|A'4(K, t ^^)|.

С увеличением пространственной частоты время выхода модуля пространственного спектра на установившееся значение монотонно убывает (рис. 2), что является характерным для нелинейных сред с тепловой, диффузионной нелинейностями [2, 4].

Четырёхволновой преобразователь излучения «вырезает» низкие пространственные частоты сигнальной волны. При этом высокие пространственные частоты сигнальной волны преобразуются им с высокой эффективностью.

Введём полуширину полосы пространственных частот ( ∆κ ), в пределах которой четырёхволновой преобразователь «вырезает» пространственные частоты сигнальной волны:

|^(к Акt)| = 2|А‘(к^~ t)|.

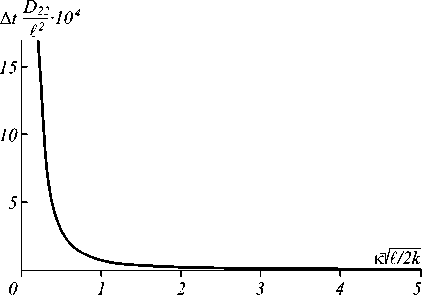
Рис. 2. Зависимость времени выхода на установившийся режим пространственного спектра объектной волны от пространственной частоты при b = 2J0-, 2kL = 104

С течением времени полуширина полосы пространственных частот монотонно уменьшается, выходя на установившееся значение (Δκ_∞) (рис. 3). Увеличение параметра b (коэффициент теплопроводности уменьшается) приводит к замедлению выхода полуширины полосы пространственных частот на установившееся значение. Значение Δκ ∞ не зависит от тепловых (d n /d T , c p , D 11 , D 12 ), электрострикционного параметров нелинейной среды, определяется только её толщиной и значением волнового числа.

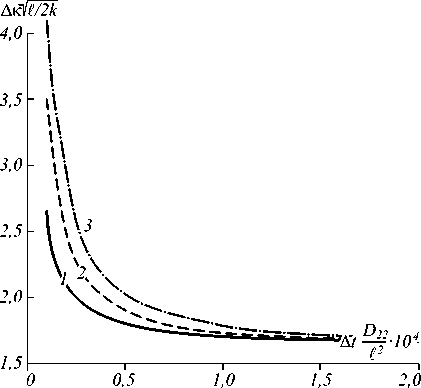
Рис. 3. Временная зависимость полуширины полосы пространственных частот, вырезаемых четырёхволновым преобразователем для 2k L = 10⁴, b = 2 H'^ (1), 0,5 (2) и 0,99 (3)

Уменьшение с течением времени полосы пространственных частот, вырезаемых четырёхволновым преобразователем излучения, свидетельствует об улучшении качества обращения волнового фронта .

Приведём оценки установившегося значения полуширины полосы пространственных частот. Будем считать, что четырёхволновое взаимодействие осуществляется излучением с длиной волны λ=532 нм в нелинейной среде с показателем преломления n 0 =1,33. Тогда при толщинах нелинейной среды

L =500 мкм, 2 мм, 1 см установившиеся значения полуширины полосы пространственных частот четырёхволнового преобразователя излучения есть Δκ_∞=4195 см^–1, 2094 см^–1, 936 см^–1 соответственно.

Заключение

Показано, что вырожденный четырёхволновой преобразователь излучения в оптически прозрачной двухкомпонентной среде с учётом электрострикции и эффекта Дюфура осуществляет фильтрацию высоких пространственных частот сигнальной волны. С течением времени полуширина полосы пространственных частот, в пределах которой четырёхволновой преобразователь «вырезает » пространственные частоты, уменьшается, что свидетельствует об улучшении качества обращения волнового фронта.