Пространственно-временные характеристики квазивырожденного четырёхволнового преобразователя излучения в прозрачной среде с учётом электрострикции и эффекта Дюфура

Четырёхволновые преобразователи излучения находят применение в системах обработки оптических сигналов, в квантовой криптографии, для получения волны с обращённым волновым фронтом (ОВФ) с последующим использованием таких волн в системах адаптивной оптики [1 – 3]. Выбор нелинейной среды и параметров излучения оказывает существенное влияние на характеристики волны с ОВФ. Переход от вырожденных ω + ω – ω = ω четырёхволновых преобразователей излучения к квазивырожденным ω 1 + ω 2 – ω 1 = ω 2 позволяет осуществлять перестройку по частоте волны с ОВФ, существенно повысить в ряде случаев эффективность таких преобразователей [4].

При создании адаптивных оптических систем могут использоваться многокомпонентные среды, позволяющие получить высокоэффективные четырёхволновые преобразователи для низкоинтенсивного лазерного излучения большой длительности в широком диапазоне длин волн [5 – 6]. Наличие в составе многокомпонентных сред наночастиц приводит к существенному влиянию на пространственную структуру волны с ОВФ таких физических процессов, как электрострикция и эффект Дюфура [7 – 10].

Цель настоящей работы – исследование пространственно-временной структуры волны с ОВФ при ква-зивырожденном четырёхволновом взаимодействии в прозрачной двухкомпонентной среде.

зультате интерференции первой волны накачки и сигнальной волны происходит изменение в пространстве интенсивности излучения. Электрострикционная сила, пропорциональная градиенту интенсивности, приводит к возникновению потока концентрации наночастиц, который из-за эффекта Дюфура изменяет температуру, а значит, и показатель преломления сре-(c   dn „ _^ _ ды I 8n = — 8T I. В результате дифракции второй I d T )

волны накачки на динамической температурной решётке генерируется объектная волна с комплексной амплитудой A ₄ и частотой ω₂, распространяющаяся навстречу сигнальной волне.

Исходные скалярные волновые уравнения, описы- вающие квазивырожденное четырёхволновое взаимо действие излучения в нелинейной среде, есть [3]

⁽ V 2 + k 2 + 3 k L.d n 8 T )( A + A * ) = 0,

1 n dT          1,31,3

Л               102         a(1)

|v ² + k 2 + 2^ d; 8 t | ( A 2,4 + A 2 4 ) = 0,

(          n20 dT)

где δ T – изменение температуры, k 1,2 = ω 1,2 n 1,20 / c , n 10 и n 20 – значения показателя преломления на частотах ω₁ и ω₂.

Система уравнений (1) дополняется системой материальных уравнений для изменений концентрации и температуры [7, 8]

^^ C = D^ ^8> C + YV ² 1 , d t        22

c p v ^I T = D 11 V 2 8 T + D 12 V 2 8 C ,

где I – интенсивность излучения, δ C – изменение концентрации частиц, D ₁₁, D ₂₂, D ₁₂ и γ – коэффициенты теплопроводности, диффузии, Дюфура и электрострикции соответственно, c_p – удельная теплоёмкость вещества, ν – плотность вещества.

• 2.    Пространственный спектр объектной волны

В приближении заданного поля по волнам накачки (| A _1,2|>>| A _3,4|) и малого коэффициента отражения (| A ₄|<<| A ₃|) интенсивность излучения, распространяющегося в нелинейной среде, можно записать следующим образом

I = I 0 ^{+ 4} A 3 ^{+ 44} ,                         (4)

где 1 0 = A 1 A * + A 2 A .

Пусть волны накачки плоские

A i,2 ( r, t ) = A i,2 ( z , t ) exp ( - ik^r ) ,                     (5)

где k₁₂ - волновые векторы волн накачки, F ( р , z ) -радиус-вектор, р ( x , y ) и z - поперечная и продольная составляющие радиус-вектора.

Сигнальную и объектную волны разложим по плоским волнам

M

A j ( r,t ) = J ^4j ( ^p j ,z , t ) exp ( - i K j p- i j ) d K j . (6)

-M где Aj - пространственный спектр j-й волны, кj и kjz – поперечная и продольная составляющие волнового вектора kj , j = 3,4.

Изменения температуры и концентрации можно представить в виде суммы быстро (δ T ₃₁, δ C ₃₁) и медленно (δ T ₀, δ C ₀) меняющихся в зависимости от координат составляющих

8 T (r, t ) = 8 T (z, t ) + 8 T31 (r, t), 8 C (p, t) = 8 C0 (z, t ) + 8 C31 (r, t).

Быстро меняющиеся составляющие температуры и концентрации разложим по гармоническим решёткам

M

8 T₃₁ ( ^p , t ) = J 8 T ₃₁ ( к _T , z , t ) exp ( - i к _T p ) d K _T ,

-M

M

8 C 31 ( ^p , t ) = J 8 C ₃₁ ( к _C , z , t ) exp ( - i к C p ) d K C ,

-M

где 8T31 и 8C31 - пространственные спектры темпе ратурной и концентрационной решёток, кT и кC - волновые векторы соответствующих решёток.

Из (1) с учётом (7) при выполнении граничного условия A 4 ( к ₄, z = I, t ) = 0 пространственный спектр объектной волны на передней грани нелинейного слоя и спектр температурной решётки связаны соотношением вида [7]

⁴ (^к 4 , z = ⁰, t ) = ^- i —T n ⁴ ; ( t ) exp [ ^- P ( t ) ] ^X n 20 d T

I xJ 8T31 (кT, z, t) exp [-i (k2z - k4z)z]dz,

k i где .420 (t ) = .42 (z = I, t), P (t ) = i — J 8T0 (z, t) dz .

n 20 0

Выражение (9) записано с учётом приближения медленно меняющихся амплитуд при квазиколлинеарном распространении взаимодействующих волн ( k 1 / k 1,3 z ≈ 1, k 2 /k 2,4 _z =-1) и условии, что к _T = к _C = к 1 - к ₃ = к ₄ - к 2 .

Для определения пространственного спектра температурной решётки воспользуемся материальными уравнениями (2)–(3). Вначале, используя уравнение (2), найдём изменение во времени пространственного спектра концентрационной решётки. Затем, подставив решение уравнения (2) в уравнение (3), найдём изменение во времени пространственного спектра температурной решётки.

При отсутствии потока частиц через грани нелинейного слоя и неизменности температуры на гранях, с учётом начальных условий 8 C ₃₁ ( к _C , z , t = 0) = 0 и 8 T ₃₁ ( к _T , z , t = 0 ) = 0, будем искать решение системы уравнений (2)–(3) в виде рядов Фурье

• /-           1/

• ^{8    C} 31 ^(к C , ^z , t ) = 2 C 0 ^(к C , t ^{) +} f n m

Cm (кC , t ) coS ; z, m =1

П S

• 8731    (кT , z, t ) = ^ Ts (кT , t ) sin — z, s=1

  
  

где C ₀, C_m , T_s – коэффициенты разложения рядов.

Подставив (10) в материальные уравнения (2)–(3), найдём изменение во времени пространственного спектра температурной решётки

⁸ T 31 (^к T , ^z , t )

2iYD12 [(k1 z - k3z )2 +кC ] cp Vn( k1 z - k3z ) 1

xA . П s > Sin — z

t

J exp

J D 11 [ c p ^v

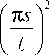
+ к T

(t-T)l J .410 (T‘) A30 (

. L 0

к 3, T‘)x

^Х ( ^к C { exp ^[- i ( ^k 1 z ^{- k} 3 z ) ^l ] ^- 1 } ^{[ 1 -}(^{- 1} ) ^S ] ^s

-J

1 exp [-D22кC (T-T')] - E{1 -(-1)m exp [-i (k1 z - k3z ) 1]}X         (11)

m =1

x

nm ]

— +к2

I J C

-

-1

n m

1 - ( - 1 ) s ⁺ m

( k1 z - k3 z ) 1

1 - ( - 1 ) "m

s + m      s - m

exp {- D 22

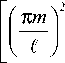
+ кC

' )

^(T-T ' ) [ ^{d T}

. 7

d T ,

где . А ю ( t ) = -4 1 ( z = 0, t ) , .4 30 ( к 3 , t ) = .4 3 ( к 3 , z = 0, t ) .

Для установившегося режима (∂δ T / ∂ t =0, ∂δ C / ∂ t =0) пространственный спектр температурной решётки имеет вид [10]

S T'       - ^YD 12 3'3к

⁰ T 31 ^(к T , z ) = р. р. A 10 A 30 ^(к 3 ^{) х} D ₁₁ D ₂₂

^X I -T—e { ^eXP [- i ( k 1 z - k 3 z ) ^l ] sh ^K T z ^- ^ sh к t l

- sh к t ( z - 1 ) } - exp [- i ( k 1 z - k 3 z ) z ] ) ,

где 0 7 3 ' 1 ( к _T , z ) = 0 T ₃₁ ( к _T , z , t ^~ ) , A^ = A ₁₀ ( t ^~ ) , A 30 ( к з ) = A 30 ( к з , t ^~ ) .

Подставив (11) в (9), получим выражение для временной зависимости пространственного спектра объектной волны

2yDnk3 [(k, - k ) + к21 ।

12 2 1z 3zC

A4 (к4 , z = 0, t) =7----—77----2—T7A1- (t) eXP [-P(t)] Д1 - (-1) eXP [i ( k2z - k4z ) 1]}X cp V n20 ( k1 z - k3 z )( k2 z - k4 z ) l dT

-1

х

-

П s

I ( k 2 z

-

k 4 z )

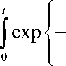
D 11 c p ^v

+ к T

( t ^-T

) | i A. м A;, (

L 0

^к 3 , ^Т ' ) ( ^к с { ^eXP ^[- i ( ^k 1 z

^{- k} 3 z ) ^l ] ^- 1 } ^X

^

X[1 -(-1)s ] exp[-D22к2 (т- T’)] - £ m =1

-1

X

n m

-

^{( k} 1 z ^{- k} 3 z ) ¹

exp

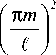
- D ₂₂

+ к ^

+ к ^

1 - ( - 1 ) ^{s +} m

₊ 1 - ( - 1 ) s^m

s + m s - m

^(T-T ' ) [ ^{d T}

/

Установившийся пространственный спектр объектной волны в результате подстановки выражения для пространственного спектра температурной решётки (12) в выражение (9) примет вид

A ‘ ( к 4 , z

= 0 ) = - i

3/ 3/ k2 YD12 A10 A20 P0 dn n20D11D22   dT

A 3" ( к 3 ) X

, ,¹ . ( { ^eXP ^[- i ( ^k 1 z ^{- k} 3 z ) ^l ] ^{- eX}P (^-к T ¹ ) } ^X 2 sh к t I^х

^exp { [ ^к T ^- i ( k 2 z ^- k 4 z ) 1 ^l } ^{- 1}

x--~---77-----/ — + к T - i ( k2 z - k4 z )

+ { eXp [- i ( k 1 _z - k _{3 z} ) l ]- eXp ( к _TI ) } x

X eXp{- [кT + i (k2z - k4z )] l}- 1 ' - к T + i ( k2 z - k4 z )

d T .

- l eXp

Г -Al² • - i— Sin c

I 2 J

A l 2

2 ^J

где . 4 4 ( к ₄, z = 0 ) = .4 4 ( к ₄, z = 0, t ^~ ) , "A 20 = "A 20 ( t ^^ ) , ^P 0 = ^eXp L ^{- P} ( t ^^ ) ] ,

A = ( k 1 + k ₂ - k 3 - k 4 ) - проекция волновой расстрой-

ки на ось Z .

Выражения (13) – (14) устанавливают однознач-

ную связь между пространственно-временными, пространственными спектрами сигнальной и объектной волн, при k 1 = k 2 совпадают с выражениями для пространственно-временного, пространственного спектра объектной волны при вырожденном четырёхволновом взаимодействии в прозрачной среде с учётом электрострикции и эффекта Дюфура [7, 10].

{ 1 ^-(^{- 1} ) m ^exp ^[- i ( k z ^- k 3 z ) ^l ] } ^X

3. Обсуждение результатов

В качестве сигнальной волны рассмотрим волну от точечного источника, расположенного на передней грани нелинейного слоя ( A ₃₀ ( к ₃, t ) = 1). Будем считать, что волны накачки распространяются строго вдоль оси Z ( к 1 = к ₂ = 0) и их амплитуды не меняются во времени. В параксиальном приближении имеем

к          .к k3 — k,--, k,. — — k + ,

3 z 1              , 4 z 2              ,

где к = |к₄| = |к₃| - пространственная частота.

На рис. 1 представлены характерные графики нормированных модулей пространственного спектра объектной волны при установившемся режиме

A n =HI

_   D„  k , l d n

2y----12--1--

D 11 D 22 n 20 d T

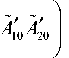
для различных отношений волновых чисел волн накачки, полученные с использованием выражения (14).

Если вырожденный четырёхволновой преобразователь излучения в прозрачной двухкомпонентной среде с учётом электрострикции и эффекта Дюфура осуществляет фильтрацию высоких пространственных частот сигнальной волны [7, 10], то квазивырож-денный четырёхволновой преобразователь, наряду с фильтрацией высоких пространственных частот, осуществляет фильтрацию и низких пространственных частот. Это является следствием ненулевой проекции волновой расстройки, входящей в явном виде в последнее слагаемое выражения (14).

Для характеристики пространственного спектра волны с ОВФ введём ширину полосы наиболее эффективно преобразуемых пространственных частот (Δκ), которая определяется из условия

Ак(t) = |к1 -K2I,

где κ1,2 – пространственные частоты, значения которых находятся из решения уравнения

| A 4 ( к=К 1, ₂, z = 0, t )| = 2 A 4max ( t ) , (17) где A 4max ( t ) = ^A 4 ( ^K = ^K max , z = ⁰, t )| ^— наибольшее значение модуля пространственного спектра, κ max – пространственная частота, на которой пространственный спектр достигает наибольшего значения.

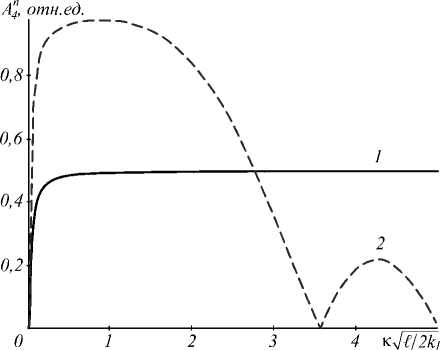
Рис. 1. Пространственные спектры объектной волны при 2k l = 100, k₂/k 1 =1 (1), 2 (2)

С течением времени ширина полосы вырезаемых четырёхволновым преобразователем частот [7], как и для случая k 2 / k 1 = 1, уменьшается, а ширина наиболее эффективно преобразуемых частот увеличивается (рис. 2).

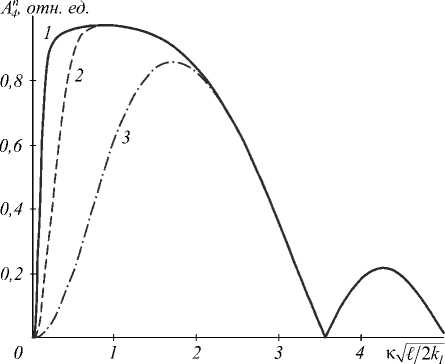
Рис. 2. Временная динамика пространственного спектра объектной волны при ^2k/ = 100, cpvD22/D11 = 2-10 5, k2/k1 = 2, tD22/ℓ2 = 10–2 (1), 10–3 (2), 10–4 (3)

С ростом пространственной частоты время выхода пространственного спектра на установившееся значение уменьшается [7]. Это объясняет совпадение видов спектров в различные моменты времени, начиная с некоторой частоты, величина которой со временем уменьшается, выходя на постоянное значение. Такую частоту можно определить по фиксированному отно- сительному отклонению модуля пространственного спектра в произвольный момент времени от значения модуля спектра для установившегося режима.

На рис. 3 для установившегося пространственного спектра представлены зависимости положения максимума κ max (кривая 1) и ширины эффективно преобразуемых пространственных частот Δκ (кривая 2) от отношения волновых чисел волн накачки. Изменение отношения волновых чисел волн накачки k ₂/ k ₁ рассматривалось в пределах от 0,1 до 10. Видно, что с увеличением отклонения отношения k ₂/ k ₁ от единицы величина Δκ монотонно убывает. При k ₂/ k ₁ → 1 диапазон эффективно преобразуемых пространственных частот охватывает всю область параксиального приближения (Δκ≈ 0,1 k ₁). Характер изменения пространственной частоты, на которой функция A ₄ достигает наибольшего значения, в зависимости от отношения волновых чисел волн накачки аналогичен изменению ширины эффективно преобразуемых пространственных частот.

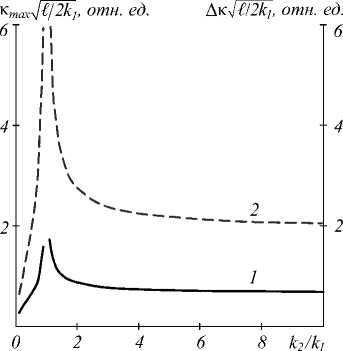
Рис. 3. Зависимость положения максимума пространственного спектра (1) и ширины полосы наиболее эффективно преобразуемых пространственных частот (2) от отношения волновых чисел волн накачки при ^ 2k 1 l = 100

Как следует из выражения (14), наибольшее значение модуля пространственного спектра объектной волны A 4max с увеличением волнового числа второй волны накачки линейно возрастает.

Вид зависимостей κmax и Δκ от отношения волновых чисел волн накачки можно объяснить, если формально представить пространственный спектр объектной волны (14) в виде суммы двух находящихся в противофазе пространственных спектров

^v        ^v^v

A4= A41 + A42,(18)

где

^/ ^

• - _ ^k 2 ¹ Y ^D 12 A 10 A 20 P 0 d n

A i^

n20D11D22d xA3* (к3) exp

^*         ^*^*

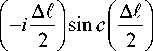
А  = А' - А

41       442

Пространственный спектр A ₄₂ определяется проекцией волновой расстройки на ось Z , совпадает с видом пространственного спектра квазивырожденного четырёхволнового преобразователя на керровской нелинейности [11]. При k 2 > k 1 вид пространственного спектра A ₄₁ определяется в основном пространственной частотой температурной (концентрационной) решётки и слабо зависит от волновых векторов волн накачки. Характер изменения пространственного спектра A ₄₁ при условии k ₂<  k ₁ становится близок к характеру изменения пространственного спектра A ₄₂ .

Уменьшение ширины Δκ с ростом отклонения от единицы отношения волновых чисел волн накачки обусловлено сужением пространственного спектра слагаемого A ₄₂ в выражении (14), свидетельствует об ухудшении качества ОВФ. При k ₂/ k ₁ → 0 ширины как пространственного спектра A ₄₁ , так и пространственного спектра A ₄₂ стремятся к нулю, что определяет стремление к нулю пространственной частоты, на которой достигается наибольшее значение пространственного спектра объектной волны, и ширины наиболее эффективно преобразуемых пространственных частот. При стремлении k ₂/ k ₁ → ∞ ширина пространственного спектра A ₄₂ , определяемая по её первому нулю, стремится к значению странственного спектра A ₄₁ Это обуславливает выход на личин как κ max , так и Δκ.

j 4Пkj I , а ширина про-– к значению 2 п к 1 /I . постоянное значение ве-

Ширина полосы вырезанных квазивырожденным четырёхволновым преобразователем пространственных частот в диапазоне отношения волновых чисел волн накачки от 0,1 до 10 при ^2 к 1 1 = 100 изменяется на 8%. Максимальное значение ширины полосы вырезанных пространственных частот соответствует вырожденному четырёхволновому преобразователю излучения.

Приведём оценки положения и ширины максимума пространственного спектра для различных толщин нелинейного слоя без учёта дисперсии. В качестве среды рассмотрим воду ( n 10 ≈ n 20 ≈ 1,333), содержащую наночастицы, в которой записываются динамические решётки излучением на длине волны λ 1 = 1064 нм. В качестве излучения второй волны накачки используется излучение с длиной волны λ 2 =532 нм. Тогда для толщин нелинейного слоя ℓ = 0,5, 1, 2 мм значения пространственных частот, на которых пространственный спектр достигает наибольшего значения, и ширины наиболее эффективно преобразуемых пространственных частот будут составлять соответственно κ max =1590, 1045, 688 см^–1 и Δκ =4868, 3447, 2440 см^–1.

Использование выражения (14) для оценки влияния немонохроматичности взаимодействующих волн на пространственную селективность четырёхволнового преобразователя в прозрачной нелинейной среде показывает, что немонохроматичность лазерных источни- ков, применяемых для записи динамических решёток (Δω / ω≤ 10–2, где Δω – спектральная ширина лазерного излучения), не влияет на ширину наиболее эффективно преобразуемых пространственных частот.

Заключение