Пространственно-временные неустойчивости в широкоапертурных лазерах

В широкоапертурных лазерах нелинейное взаимодействие большого числа поперечных мод может приводить к спонтанному появлению сложных пространственновременных оптических структур. В широкоапертурных лазерах экспериментально наблюдаются автоволны [1], решётки оптических вихрей [2, 3], солитоны [4] и другие нелинейные пространственно-временные оптические структуры, включая хаотические. Теоретически предсказано существование спиральных волн [5]. Как правило, существование подобных структур оказывается нежелательным, так как может ухудшать качество оптического излучения. Поэтому часто размеры выходной апертуры стараются ограничивать, чтобы избежать усложнения поперечной структуры пучка. Однако для многих технических приложений требуется создание именно широкоапертурных устройств. В частности, ввиду конструктивных особенностей мощный полупроводниковый лазер должен обладать большой шириной активной области, достигающей сотен микрометров. В таких полупроводниковых диодах пространственные эффекты начинают играть значительную роль, приводя к усложнению поперечного профиля излучения [6].

В работе [7] с помощью автомодельной системы уравнений Максвелла–Блоха было показано, что лазерная модель в случае бесконечно широкой апертуры допускает решение вида бегущей волны. При изменении управляющих параметров происходит переход к пространственно-временному хаосу через последовательность бифуркаций удвоения двумерного тора. Устойчивость автомодельного решения на конечной апертуре была исследована в [8]. Однако в обеих работах использовалась укороченная система уравнений с адиабатически исключённой поляризацией и проведён лишь однопараметрический бифуркационный анализ. В данной работе с помощью полной системы лазерных уравнений Максвелла–Блоха проведён многопараметрический анализ устойчивости режима пространственно-однородной генерации широкоапертурного лазера, проведено численное моделирование. Параметры модели выбирались из соображений максимальной приближённости к реальным лазерам.

Основные уравнения. Линейный анализ

В качестве исходной рассмотрим полную систему уравнений Максвелла–Блоха [9]:

д E ■ д 2 E

— = a —г + g P - E ,

д t        д x ^{2      (}       )

a p a t a d д t

= -(1 +i5)P + DE,

= -Y D-r + 2(E-P + EP') •

E , P , D – безразмерные огибающие электрического поля, поляризации и инверсии населённости соответственно; у = Уц/у_± и а = к /у_± , где к , у_± и y_h - ско-

рости релаксации поля, поляризации и инверсии населённости соответственно; 5 = ( ю ₂₁ -ю)/у_± - расстройка между центром линии усиления и частотой генерации, обезразмеренная на полуширину линии; a = c У( 2 юу_± b ² ) - дифракционный параметр, где b -

единица длины в модели, c – скорость света в вакууме; r – накачка, нормированная на пороговое значение; единица времени в модели равна у ^ ¹.

В работе [10] показано, что в зависимости от знака параметра отстройки 5 существует два качественно различных случая динамики лазера. При 5 >  0 реализуется решение вида бегущей волны, соответствующее устойчивой внеосевой генерации – в таком случае в дальнем поле лазерного излучения наблюдается единственное яркое пятно, смещённое от центра. При 5 <  0 реализуется режим генерации пространственно однородного излучения – в таком случае в дальнем поле наблюдается центральное яркое пятно. В данной работе исследуется случай отрицательной отстройки 5 <  0 , тогда пространственно однородное решение системы (1) имеет вид:

D st

= 1 +

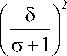
E st = ( r - D_M ) ^0. 5 • e^{- i} ^ t ,

_ (о- i Q ) . E st

P st

,

о

Q= SO

G + 1

.

При этом интенсивность излучения лазера I = E |2 получается не зависящей ни от времени, ни от пространственных координат. Однако по мере увеличения накачки данное пространственно однородное состояние может потерять устойчивость, следствием чего станет установление другого, более сложного режима генерации. Такое бифуркационное значение управляющего параметра лазера, соответствующее порогу неустойчивости режима стационарной генерации, называется вторым порогом генерации. Нахождение второго порога генерации сводится к исследованию на устойчивость решения (2). Для этого линеаризуем систему (1), полагая:

E = (| E st | + e , ■ e qx ^+x t + e 2 ■ e ^{- iqx +x} * t ) ■ e ^{- i Q} t ,

P = (| p st | + p 1 ■ e iqx ^+x t + p 2 ■ e ^{- iqx +x} ’ t ) ■ e ^{- i Q} t ,              (3)

*

D = Dst + d ■ eq+xt + d * ■ e-,qx+x t, где e1 , e2 , p1 , p2 , d – малые возмущения соответствующих величин, q – волновой вектор возмущения. В результате подстановки решения (3) в систему (1) задача сводится к нахождению собственных чисел X матрицы линеаризации, имеющей размеры 5×5. Решение (2) будет устойчивым по отношению к малым возмущениям, если все собственные числа будут иметь отрицательные действительные части при всех значениях q . Наличие же положительных действительных частей у показателей экспоненты при некоторых значениях q свидетельствует о росте соответствующих малых возмущений с течением времени, то есть о неустойчивости решения (2). Определение собственных чисел матрицы линеаризации проводилось численно.

Важными с практической точки зрения являются широкоапертурные полупроводниковые лазеры. Для полупроводниковых лазеров характерны следующие параметры [11]:

• Y_±« 10¹³ c ^{- 1} k « 5 ■ 10¹¹ c ^{- 1} y_H » 5 ■ 10 9 c ^{- 1} ,,, тогда о = 5 ■ 10 ^{- 2} и y = 5 ■ 10 ^{- 4}.

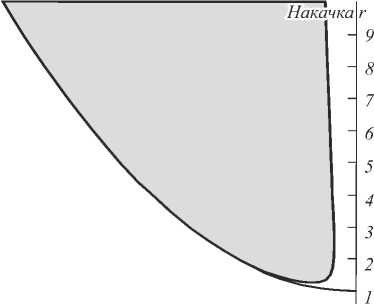
Единица модельного времени в таком случае равна 0,1 пс. Воспользовавшись описанным выше методом, построим бифуркационную диаграмму в плоскости параметров ( S , r ) . На рис. 1 сплошной кривой отмечен порог лазерной генерации. Серым цветом отмечена область лазерных параметров, при которых режим пространственно однородной стационарной генерации оказывается неустойчивым по отношению к малым возмущениям.

Таким образом, проведённый анализ позволяет выделить область лазерных параметров, при которых возможны сложные режимы лазерной генерации. На рис. 2 показана дисперсионная кривая, построенная при параметрах, взятых из области неустойчивости вблизи границы неустойчивости.

-3,0   -2,5 -2,0    -1,5 -1.0 -0,5       0

Отстройка б

Рис. 1. Бифуркационная диаграмма при о = 5 ■ 10 ^{- 2} и Y = 5■Ю ^{- 4}

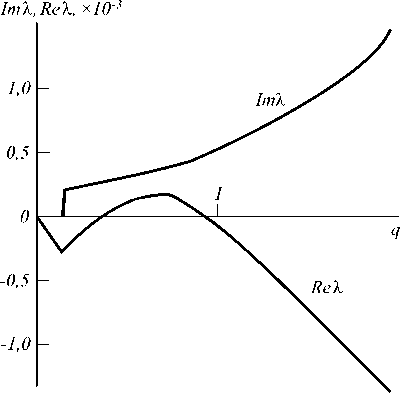
Рис. 2. Дисперсионная кривая при r = 2, δ = –0,5, α = 0,01

Действительная часть собственного числа (инкремент) имеет максимум на некотором волновом числе qmax . При этом мнимая часть корней оказывается ненулевой, то есть имеет место пара комплексно сопряжённых корней. Такой тип дисперсионной кривой соответствует волновой неустойчивости [12], в результате которой образуется бегущая волна с волновым числом qmax и частотой Im X(qmax). Для рассматриваемой области параметров qmax ® 0,76 (рис. 2), тогда минимальный размер пространственной области, на которой возможно развитие такой неустойчивости, равен Lmin = 2п/qmax ® 8,27 безразмерных единиц или, переходя к размерным величинам, Lmin = Lmin (c2/2toY±a)/ . Тогда для лазера с длиной волны генерации, равной дающих в область неустойчивости на рис. 1, следует ожидать образования нелинейных пространственновременных структур оптического поля. В лазерах, не обладающих достаточной шириной активной области, режим стационарной генерации оказывается устойчивым.

Численное моделирование

Нелинейную стадию развития возмущения мы исследовали численно. В данной работе для численного моделирования использовался широко известный псевдоспектральный метод Split Step Fourier Method [13]. Моделирование проводилось при следующих параметрах: а = 5 - 10 - 2 , у = 5 - 10 - 4 , a = 0,01. Интегрирование проводилось с временным шагом т = 0,01, использовалась пространственная сетка из 256 элементов. В качестве начальных условий был выбран пространственно однородный режим лазерной генерации (2) с добавлением шума малой амплитуды. Моделирование проводилось с периодическими граничными условиями. При выборе параметров δ и r из области устойчивости (рис. 1) наблюдается пространственно однородный режим генерации при любых размерах пространственной области L . Если же выбрать параметры из области неустойчивости, то динамика лазера зависит от размеров пространственной области. Подробно рассмотрим пример динамики лазера при r = 2, 5 = - 0,5 (соответствующая дисперсионная кривая приведена на рис. 2). Моделирование пространственно-временной динамики при L <  L min показало, что режим пространственно однородной генерации оказывается устойчивым, несмотря на наличие неустойчивых мод. Неустойчивые моды начинают развиваться только в случае L >  L min . На начальной стадии развития генерации наблюдаются две встречные бегущие волны с волновым числом q _max , соответствующим максимуму на дисперсионной кривой. Однако в дальнейшем происходит серия переключений между различными пространственными модами, сопровождаемая сменой характерного пространственного размера (рис. 3).

На рис. 4 хорошо видно, что до 12 нс в пространственном спектре присутствует лишь нулевая компонента, т.е. поперечный профиль до этого момента остаётся квазиоднородным, затем в спектре появляются дополнительные компоненты. В дальнейшем развитие возмущений приводит к более сложной динамике, хорошо видны переключения между различными пространственными модами.

Численное моделирование подтверждает корректность построенной бифуркационной диаграммы (рис. 1), т.к. сложная пространственно-временная динамика наблюдается только при параметрах из выделенной на диаграмме области неустойчивости. Характерные размеры лазерной апертуры, при которых поперечные эффекты начинают играть важную роль, также совпадают с размерами, предсказанными в результате линейного анализа. На нелинейной стадии развития возмущения наблюдаются переключения между различными пространственными модами, происходящие с частотой порядка 1 ГГц.

Координата х, мкм

Рис. 3. Пространственно-временная динамика ближнего поля лазера при а = 5 - 10 ^{- 2} , у = 5 - 10 — 4 , r = 2 , 5 = - 0,5 , a = 0,01 , L = 20

Рис. 4. Динамика дальнего поля лазера при а = 5 - 10 ²

Y = 5 - 10 — 4 , r = 2 , 5 = - 0,5 , a = 0,01 , L = 20

Заключение

Проведён анализ устойчивости пространственно однородного режима генерации. Показано, что в таких лазерах реализуется волновая неустойчивость, построена бифуркационная диаграмма. Определены размеры апертуры, при которых возможно развитие волновой неустойчивости. Проведено численное моделирование пространственно-временной динамики лазера, подтвердившее выводы линейного анализа. На нелинейной стадии развития возмущения наблюдаются переключения между различными пространственными модами.

Работа частично поддержана Минобрнауки РФ в рамках Программы повышения конкурентоспособности СГАУ на 2013–2020 гг. и Государственного задания вузам и научным организациям в сфере научной деятельности, проект 1451, НИР №ГР 114091840046, грантом РФФИ 14-02-31419 мол_a.