Пространственное интегрирование оптических пучков с использованием многослойных брэгговских структур
Автор: Головастиков Никита Владимирович, Быков Дмитрий Александрович, Досколович Леонид Леонидович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 3 т.38, 2014 года.
Бесплатный доступ
Рассмотрена дифракция двумерного оптического пучка на многослойной брэгговской структуре. Показано, что брэгговская решётка с дефектом позволяет выполнить операцию пространственного интегрирования двумерного профиля падающего пучка с центральной пространственной частотой, близкой к константе распространения квазиволноводной моды дефектного слоя. Пространственное интегрирование осуществляется в пропускании с экспоненциальной весовой функцией, скорость затухания которой определяется величиной добротности резонанса. Результаты электромагнитного моделирования показывают хорошее соответствие численных результатов приведённому теоретическому описанию.
Брэгговские структуры, резонанс, оптическое интегрирование
Короткий адрес: https://sciup.org/14059249
IDR: 14059249
Текст научной статьи Пространственное интегрирование оптических пучков с использованием многослойных брэгговских структур
Пространственно-временные преобразования оптических пучков представляют большой интерес для решения широкого круга задач, включающих формирование оптических импульсов и пучков заданной формы, аналоговые оптические вычисления, сверхбыструю оптическую обработку информации [1, 2].
Ранее была описана способность брэгговских решёток с дефектом (phase-shifted Bragg grating) осуществлять временные преобразования оптических сигналов, включающие дифференцирование огибающей оптического импульса в отражении [2–4] и интегрирование огибающей импульса в пропускании [5].
Пространственное дифференцирование двумерных оптических пучков впервые было рассмотрено в работе [6]. В [6] показано, что брэгговская решётка с дефектом позволяет выполнить операцию дифференцирования пространственного профиля двумерного оптического пучка в отражении. В данной работе впервые показано, что брэгговские решётки с дефектом позволяют выполнить операцию пространственного интегрирования двумерного профиля падающего пучка в пропускании.
Дифракция пучка на многослойной структуре
Рассмотрим наклонное падение двумерного оптического пучка на многослойную структуру (систему однородных слоёв). Пучок распространяется в отрицательном направлении оси z в системе координат ( x, z ), связанной с пучком и повёрнутой относительно системы координат многослойной структуры ( x ml , z ml ) на угол 6 0 (рис. 1). В этой системе координат разложение падающего пучка по плоским волнам имеет следующий вид:
P nc ( x , z ) =
= JG(kx) exp{ikxx-iVk02n2» - kxz}dkx, ( ) где G(kx), | kx | < g - угловой спектр пучка, k0 = 2л/% -волновое число, kx = k0nsupsin 6 и kz = ^k02ns2up - k^2 - компоненты волновых векторов падающих волн, nsup – показатель преломления среды над структурой. Функция Pinc(x, z) соответствует компоненте Ey электрического поля в случае ТЕ-поляризации и компоненте Hy магнитного поля в случае ТМ-поляризации.
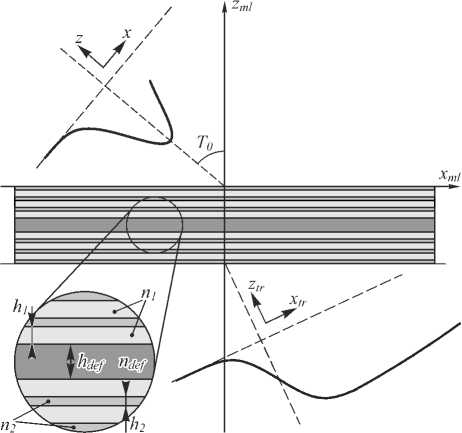
Рис. 1. Дифракция оптического пучка
В результате дифракции пучка на многослойной структуре прошедшее поле примет вид:
Ptr( x tr , z tr ) =
= J G ( kx ) T ( kx ) exp {ikxxtr - iVk02ns2ub - k2 ztr } dkx , (2) где T (kx ) – комплексный коэффициент пропускания структуры, а k%x = k0nsup sin (6+60 ) = kx cos 60 + Vk02 ns2up - k2 sin 60 соответствует x-компоненте волнового вектора, падающего на решётку под углом 6 + 60 в системе координат многослойной структуры (xml, zml). Отметим, что выражение (2) записано в системе координат, связанной с преломлённым пучком (рис. 1). При этом полагаем, что начала координат в системах (x, z) и (xtr, ztr) совпадают с началом координат системы (xml, zml).
Предполагая, что спектр падающего пучка является достаточно узким ( g << k 0 n sup ), получим:
k x ” kx cos 9 0 + k 0 n sup sin 9 0 = kx cos 9 0 + kx ,0 , (3) где kx ,o = k о n supsin 9 0 - центральная пространственная частота падающего пучка. Рассмотрим связь профиля падающего пучка P inc ( x ,0) с профилем прошедшего пучка P tr ( x tr ,0). Из (1), (2) можно заключить, что преобразование профиля падающего пучка P inc ( x ,0) в профиль P tr( x ,0) можно описывать в терминах прохождения сигнала через линейную систему с передаточной функцией (ПФ) вида:
H tr ( k x ) = T ( k x cos 9 o + k x^ ) . (4)
Отметим, что ПФ (4) по виду аналогична ПФ, описывающей преобразование временного оптического импульса [7].
Интегрирование пучка в пропускании
Покажем, что брэгговская решётка с дефектом может использоваться для интегрирования оптических пучков в пропускании.
Рассмотрим брэгговскую структуру, состоящую из двух симметричных брэгговских решёток, разделённых слоем дефекта. В простейшем случае один период брэгговской решётки состоит из двух слоёв с одинаковой оптической длиной пути:
n 1 h 1 = n2 h 2 = % B /4, (5)
где n = Jni -(nsupsin 90) , i = 1,2, ni, hi - коэффициенты преломления и толщины слоёв решётки и %B -брэгговская длина волны. Пусть также оптическая толщина слоя дефекта равна ndefhdef = %B /2, где ndef = ^ndef -( nsupsin 90 ) , где ndef – коэффициент преломления слоя дефекта. При выполнении этих условий коэффициент отражения брэгговской решётки на длине волны %B при угле падения 90 будет обращаться в ноль одновременно для TE- и TM-поляризованных плоских волн [3,5]. Отметим, что указанный ноль отражения находится в центре первой фотонной запрещённой зоны брэгговской решётки.
Наличие нуля отражения связано с возбуждением в слое дефекта квазиволноводной моды. В окрестности волноводного резонанса коэффициент пропускания может быть приближенно представлен в следующем виде [7–9]:
T ( k x ) = a +
b
%
b
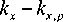
kx + k» x x , p
где a – нерезонансный коэффициент пропускания, b – коэффициент, описывающий резонансное рассеяние света на структуре, k x , p – комплексная константа распространения собственной моды брэгговской структуры, соответствующая полюсу функции
T ( k x ) . Отметим, что коэффициент пропускания (6) является чётной функцией угла падения и поэтому содержит два резонансных слагаемых, соответствующих модам с константами распространения ± k x , p , возбуждаемых при k x = k x , 0 = ± Re k x , p . Далее будем считать, что брэгговская структура имеет достаточно большое количество слоёв, так что нерезонансный коэффициент пропускания a =0 в (6).
Рассмотрим вначале дифракцию наклонно падающего пучка. При этом будем считать, что значение центральной пространственной частоты падающего пучка kx ,0 достаточно велико, так что можно пренебречь влиянием на спектр (6) полюса с противоположным знаком – kx , p и, соответственно, пренебречь последним резонансным слагаемым в (6). В этом случае получим:
l(kx V ^-b ---. (7)
1 x1 k - kxp x x , p
С учётом условия | T ( k x ,0 ) | = 1 запишем постоянную b в виде:
I b l = k x ,0
-
k x , p .
ПФ (4) с учётом вида коэффициента пропускания (7) принимает вид:
H ( k x ) =
b kx cos 90 -( kx,p - kx,0 )
Исследуем вид преобразования, которое выполняет над входным сигналом линейная система с ПФ вида (9). Для этого запишем импульсную характеристику системы, выполнив обратное преобразование Фурье от ПФ (9):
1 ^
h ( x ) = 2 П J" H ( kx ) e xp { i kx x } d kx = -^
= sgn(Im kx,p)-^b- exp ji kx’p kx,0 Л x (10) x ' cos 90 [ cos 90 J xu (sgn ( Im kx,p )• x) , где sgn(x) – функция знака, u (x) – функция единичного скачка. Интеграл в (10) вычислен с использованием теоремы Коши о вычетах и леммы Жордана. Согласно (9), в зависимости от положения полюса kx,p в верхней или нижней полуплоскости, импульсная характеристика отлична от нуля при x >0 и при x <0 соответственно.
Используя выражение для импульсной характеристики (10), представим профиль прошедшего пучка в виде интеграла с переменным верхним пределом от падающего пучка с экспоненциальным весом:
x
/ tr ( x ,0 ) = J h ( x - S ) P nc ( x ,0 ) d ^ =
C x j k - k .1
= i b J exp ^ i ( x - ^) ———- [ P nc ( x , 0 ) d ^ , c [ cos 9 0 J
где C = -^ • sgn (Imkx,p). Из (9), (11) следует, что идеальное интегрирование с единичной весовой функци- ей будет осуществляться при kx,p ^ kx,0. В этом случае, согласно (8), | b |^0 и амплитуда выходного сигнала будет также стремиться к нулю в соответствии с (11). Таким образом, идеальное интегрирование невозможно, поскольку соответствует случаю нулевой энергии прошедшего сигнала. Отметим, что условие kx,p ^ kx,0 означает, что Imkx,p ^ 0. При уменьшении Im kx,p увеличивается добротность резонанса. Соответственно, для «приближения» к идеальному интегрированию следует использовать многослойные брэгговские структуры с высокодобротными резонансами.
Далее рассмотрим случай нормального падения, когда нельзя пренебречь вторым слагаемым в представлении (6). В этом случае, используя теорему о вычетах, получим импульсную характеристику системы в виде:
h (x ) = 1 7-------^p------7
2 п ( k x - k x , p )( k x + k x , p )
exp { i k x x } d k x =
= sgn ( Im k x , p ) • i b exp { sgn ( Im k x , p ) • i k x , p |x |} .
Отметим, что поскольку коэффициент пропускания (6), в отличие от (7), имеет полюсы и в верхней, и в нижней полуплоскости, то прошедший сигнал будет являться не интегралом от падающего пучка, а свёрткой падающего сигнала с двусторонней экспонентой. Согласно (12), при уменьшении Im kx,p (при увеличении добротности резонанса) ширина импульсной характеристики и прошедшего сигнала будет возрастать.
Результаты расчётов
В качестве примера рассмотрим брэгговскую структуру, состоящую из двух симметричных брэгговских решёток с 5, 7 и 9 периодами и центрального слоя дефекта. Показатели преломления материалов слоёв брэгговских решёток, дефекта, материалов областей над и под структурой зададим в виде: n 1 = 1,5, n 2 = 2,25, n def = 1,5, n sup = n sub = 1. Толщины слоёв брэгговских решёток определены из уравнения (5) для % в = 1500 нм и 6 0 = 30°.
На рис. 2 представлены модули ПФ брэгговских структур с вышеуказанными параметрами для случая ТЕ-поляризации. Сплошными линиями показаны расчётные спектры пропускания брэгговских структур, а пунктирными – спектры, вычисленные в рамках используемого приближения (7). Рис. 2 показывает, что с увеличением числа периодов уменьшается ширина пика пропускания (возрастает добротность резонанса) и ПФ по форме приближается к ПФ идеального интегратора. Для расчёта спектров пропускания использовался вариант метода фурье-мод из работы [10]. Для расчёта аппроксимаций спектров (7) были вычислены константы распространения собственных квазиволноводных мод брэгговских структур: kx,p = 2,099 + 0,103i мкм-1 для случая пяти периодов, kx, p = 2,095 + 0,017i мкм-1 для семи периодов и kx,p = 2,094 + 0,003i мкм-1 для девяти периодов. Константы kx,p были рассчитаны как полюса матрицы рассеяния с использованием численного алгоритма, основанного на поиске максимального собственного числа матрицы рассеяния [11]. Приведённые значения констант распространения также показывают уменьшение Im kx,p (увеличение добротности резонансов) при увеличении числа периодов в брэггов-
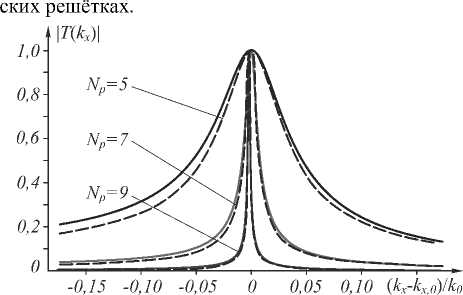
Рис. 2. Модуль передаточной функции брэгговской структуры при различном числе периодов
На рис. 3 представлен результат дифракции ТE-поляризованного Гауссова пучка с профилем P inc ( x ,0) = exp(- x 2/ o 2), о = 3,5 мкм и с центральной пространственной частотой k x ,0 =2,1 мкм –1 на брэгговских структурах для случаев 5, 7 и 9 периодов.
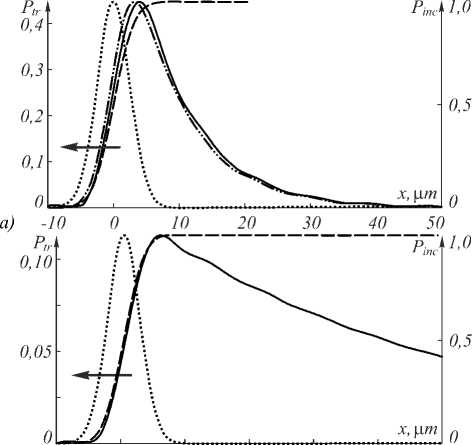
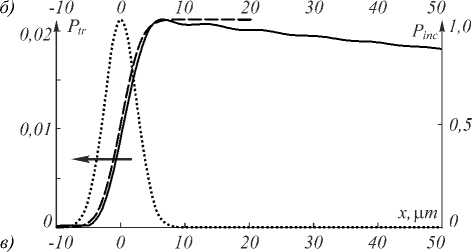
Рис. 3. Сравнение формы прошедшего пучка с аналитически вычисленной первообразной для брэгговских структур при различном числе периодов:
5 периодов (а), 7 периодов (б), 9 периодов (в)
На рис. 3 представлены профили прошедшего пучка P tr ( x tr,0), рассчитанные по формуле (2) (сплошные линии), аналитически вычисленная первообразная (пунктирные линии) и профиль падающего пучка (точечные линии, шкала справа). В качестве примера на рис. 3 а также приведён профиль прошедшего пучка, вычисленный с использованием выражения (11) (штрихпунктирная линия). Данный профиль хорошо совпадает с расчётным профилем, что подтверждает корректность использованного приближения (7). Отметим, что для случаев на рис. 3 б , в профиль прошедшего пучка фактически полностью совпадает с профилем, рассчитанным по формуле (11).
Графики на рис. 3 демонстрируют эволюцию формы прошедшего пучка при увеличении числа периодов брэгговских решёток в структуре. Видно, что с увеличением числа периодов форма прошедшего пучка приближается к функции erf( x /σ), являющейся первообразной от профиля падающего Гауссова пучка. Одновременно с этим уменьшается амплитуда прошедшего пучка, что находится в соответствии с выводами предыдущего пункта.
Рассмотрим далее дифракцию нормально падающего пучка на брэгговской структуре. При этом толщины слоёв брэгговских решёток определяются формулой (5) для θ 0 = 0, а число периодов брэгговских решёток в структуре равно 7. На рис. 4 приведены рассчитанный профиль прошедшего пучка (сплошная линия), профиль, полученный в рамках приближения (6) в виде свёртки падающего профиля с импульсной характеристикой (12) (штрихпунктир-ная линия), а также профиль падающего пучка (точечная линия, шкала справа).
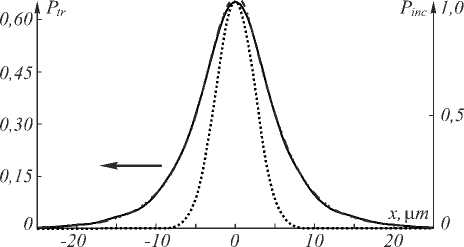
Рис. 4. Профиль прошедшего пучка в случае нормального падения
Рис. 4 показывает высокую степень совпадения расчётного профиля и профиля, рассчитанного в рамках приближения (6). При этом полуширина падающего и прошедшего пучков по уровню 1/e составляют σ inc = 3,5 мкм и σ tr = 6,2 мкм, соответственно.
Заключение
Рассмотрена возможность осуществления интегрирования пространственного двумерного профиля падающего пучка в пропускании с использованием брэгговской решётки с дефектом.
Рассмотрены случаи нормального и наклонного падения. Показано, что возможно осуществление пространственного интегрирования падающего пучка вдали от нормального падения. На численном примере продемонстрировано, что с увеличением числа периодов брэгговских решёток, образующих структуру, растут добротность резонанса и качество интегрирования при одновременном уменьшении энергии прошедшего пучка. Результаты электромагнитного моделирования с высокой точностью подтверждают приведённые теоретические оценки.
Исследование выполнено за счёт гранта Российского научного фонда (проект № 14-19-00796).


