Пространственные структуры в двухвозрастной популяции: пространственно-временной хаос, химеры и уединенные состояния

Для многих видов животных и растений характерно неравномерное распределение особей по ареалу. Независимо от причин оно проявляется в том, что на разных участках наблюдается существенная разница в численностях (плотностях) и, часто, характере динамики [3, 4]. Одна из возможных причин этого связана с особенностями расселения (миграции) особей на удаленные территории, которая не всегда способна приводить к полной синхро- низации [1, 5]. Данная работа посвящена изучению механизмов синхронизации и десинхронизации динамики пространственно разобщенных двухвозрастных популяций, приводящих к сложным стационарным или нестационарным пространственным структурам (пятна, полосы, спирали, волны и т.п.) в распределении особей по ареалу. Рассматривается следующая система рекуррентных уравнений [1]:

'xi, j (t + 1) = a yt, j (t) exp(- xx, j (t) - yi j (t)), i+P j+P yt,j(t + 1) = rxi,j(t) + y i,j(t) +      ^ ^M(i, j, g, h)(yg,h(t) - y,,j(t)),

C g = i - Ph = j - P

M ( i, j , g , h ) = И( i — g ) 2 + ( j — h ) 2 — P ² ) exp f- ^{( i} — g ^{) 2} + ⁽ j — h ^{) 2} 1 C                       I ^P )

где xi,j(t) и yi,j(t) – относительная численность или плотность неполовозре- лей. Показатель синхронизации:

лой и половозрелой частей популяции на участке с номером i , j ( i =1,2,…, s , j =1,2,…, k ). Ареал имеет прямоугольную форму и состоит из sk участков. Границы ареала замкнуты, для чего

R -

ks

, где

используются периодические граничные условия. Параметр a – коэффициент рождаемости; s и v – коэффициенты выживаемости каждой возрастной группы; ρ определяет степень участия молоди в плотностно-зависимой регуляции рождаемости; m и P – сила и радиус связи; Θ – функция Хевисайда.

Исследование системы (1) показывает, что порождаемые ею пространственно-временные режимы сочетают когерентные и некогерентные режимы на разных участках, а также уединенные состояния. Когерентные режимы включают в себя полную и кластерную синхронизацию, которая проявляется в виде пятен, полос или лабиринтов из полностью когерентных точечных популяций. Некогерентные режимы включают в себя химерные состояния, при которых на ареале сосуществуют кластеры или отдельные популяции с принципиально разными режимами, а также популяции с выбросами численности (уединенные состояния). Показано, что разным начальным условиям, которые не сильно отличаются между собой, соответствуют принципиально разные режимы пространственно-временной динамики.

Для исследования отмеченной мультистабильности предлагается использовать следующий ряд показате- ks               T

Ft- й XX yj), U=X u (t), k s i-1 j-1                    T T0 t - T - To который позволяет идентифицировать режимы, близкие к полной синхронизации. Параметр порядка:

1ks zt - Pe exp(i ^>t)- — X XexpWg,h(t)), ks g-1 h-1

который позволяет оценить степень близости фаз колебаний разных популяций.

Для величин R и z применима следующая схема интерпретации их значений. Близость R и модуля параметра порядка ρ=|z| к 1 указывает на режим динамики, близкий к полной синхронизации. Однако в случае кластерной синхронизации и, как следствие, пятнистого распределения R резко падает и приближается к нулю при усложнении узоров. В то же время ρ остается достаточно высоким и плавно уменьшается при усложнении формы узоров и характера динамики. При этом величины R и ρ слабо чувствительны к появлению небольшого числа уединенных состояний. Поэтому в дополнение предложен способ оценки числа уединенных состояний S, подробное описание которого можно найти в [2]. При проведении численного анализа генерировалось множество случайных начальных условий и на основе этих показателей оценивалась вероятность формирования того или иного режима пространственно-временной динамики (рис.).

Показано, что по мере снижения силы или радиуса связи падает вероятность формирования «простых» когерентных режимов (пятен, полос, лабиринтов) и растет вероятность

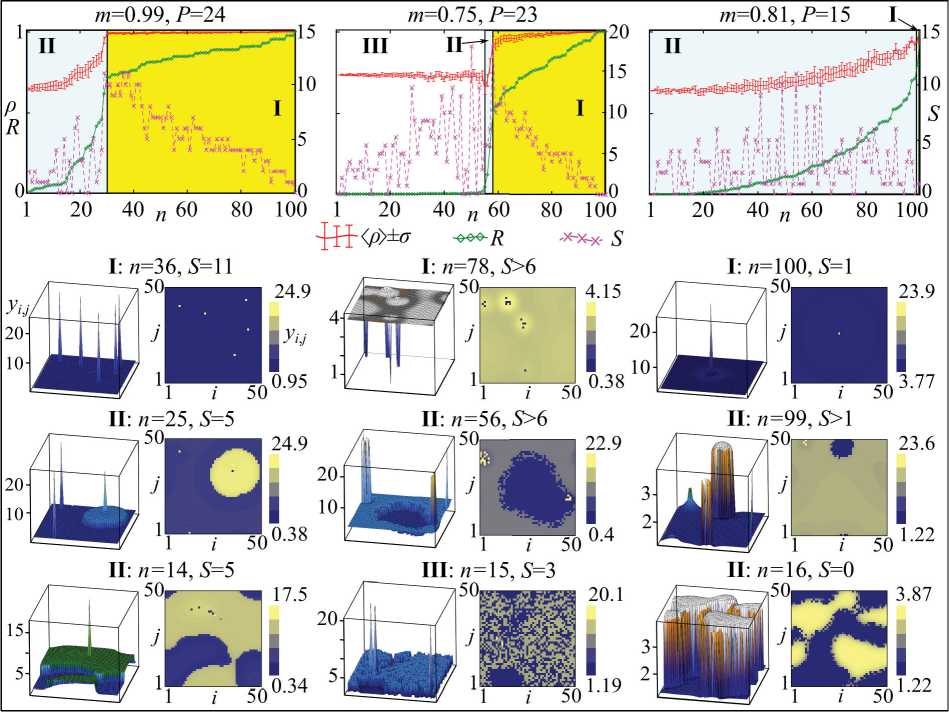
Рис. Верхний ряд – изменение амплитуды параметра порядка ρ _t , показателя синхронизации R и числа уединенных состояний S, наблюдаемых для начальных условий под «номером» n. Нижние ряды – примеры пространственных структур, соответствующие разным типам пространственно-временной динамики: I – равномерное распределение с полной или частичной синхронизацией, II – неоднородное распределение с кластерной синхронизацией, III – распределение с сильно раздробленными пятнами

Fig. The top row shows the change in amplitude of the order parameter ρ _t , the synchronization factor R and the number of solitary states S observed for the initial conditions with the “number” n. The bottom rows show the examples of spatial patterns corresponding to different types of space-time dynamics: I is a homogeneous spatial distribution with complete or partial synchronization; II is a heterogeneous distribution with cluster synchronization; III is a highly fragmented distribution

«сложных» некогерентных режимов при близких начальных условиях. Выявлена следующая парадоксальная ситуация. По мере того, как элементы оказываются менее связанными, а их динамика менее согласованной (некогерентной), число уединенных состояний увеличивается. Однако впоследствии элементы с выбросами все чаще синхронизируются между собой и начинают образовывать кластеры, перемешанные с кластерами синхронных популяций. В результате на ареале можно выделить несколько групп популяций разного размера (кластеров) с принципиально разным типом динамического поведения (отличаются периоды и амплитуды колебаний). В крайней ситуации при слабой связи кластеры на основе уединенных состояний появляются на фоне абсолютно несинхронной динамики, например, на фоне пространственно-временного хаоса [2].