Простые стационарные фильтрационные потоки несжимаемой неньютоновской нефти в однородном пласте по общему нелинейному закону

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 622.654.12                                     

Рассмотрены варианты решения трех стационарных гидродинамических задач, в которых процессы фильтрации подчиняются только общему нелинейному закону [1–5]. В первой задаче фильтрация нефти происходит с плоскопараллельным простым потоком.

На Рисунке 1, показана схема системы «прямолинейная галерея — полосообразная залежь», в котором представлены следующие условные обозначения: Pп — пластовое давление; Рг — забойное давление галереи; динамическое забойное давление галереи; P — текущее давление; x — пространственная координата (абсцисса); Lk — длина залежи; h — мощность (толщина) продуктивного.

>

	..............
ЖВЖВЖ
<--------------------

х

Рисунок 1. Схема системы, «прямолинейная галерея — полосообразная залежь»

Нелинейный закон фильтрации общий нелинейный, в дифференциальной форме выражается, в виде:

/ dP 1' и=— C т

V dx J где С — коэффициент фильтрации (подвижности); 1 _ показатель степени.

n

Площадь поверхности фильтрации, будет:

F = B • h,

где B — ширина полосообразной залежи.

Используя значения υ и F в формулах (1) и (2), получаем следующее дифференциальное уравнение:

Q = и F =

—

n

■ BhC dP I

\ dx J

где Q — дебит нефти галереи.

Разделяя на переменные уравнение (3) и интегрируя его в пределах по P от P k до P г и x от нуля до L k , получаем следую формулу для дебита галереи:

Q =

BhC ( P k — P r ) ¹

L

n k

Скорость фильтрации неньютоновской нефти, будет:

u =

С ( P k — P. $

n

Lk

Как видно из формулы (5), текущая скорость фильтрации не изменяется в зависимости от пространственной координаты, т. е. от абсциссы x , а остается постоянной.

А теперь интегрируем уравнение (3) в других пределах, т.е. по P от Pk до P и по x от Lk до x:

Q 1 BhC J

x        P k

J dx = j dP

P

[~~Rhc\ ⁽ x - L^k ) = P - P ^.

V BhC J

Подставляя значение Q из формулы (4) в формуле (6) получаем следующее выражение для закона распределения текущего давления в данной полосообразной залежи:

P = P

k

—

L k

—

x

( P - P r ) ¹ .

Lⁿ k

Дифференцируя P по x в формуле (7), получаем следующее выражение для текущего градиента давления в данной залежи:

dP dx

— Л ( Pk — P r ) ¹

n

Lk

Для определения значения частичной продолжительности продвижения нефти, используем. Эту известную аналитическую связь:

и

to = — = mdt

Где ω — средняя истинная скорость движения нефти в поровых каналах пласта, m —

коэффициент пористости формуле (9), получаем:	пласта, t — время. Подставляя значение υ из формулы (5) в ± ( P — Pr) 1 = dx                                   (10) mLn            dt
Отсюда имеем:	1                                                               (11) mLn dt =----- k—r dx C ( P — P ) "

Интегрируя уравнение (11) в пределах по t от нуля до t и по x от x до Lk, получаем: 1

t =   ₍ mL , ( L — x )

C ( P k — P r ) n

По формуле (12) вычисляется значение частичной продолжительности продвижения несжимаемой неньютоновской нефти в однородной полосообразной залежи от текущего положения x до галереи. При x=0; t=T имеем:

1+ n

mLkn

C ( P — P ) т

По формуле (13) определяется значение полной продолжительности продвижения нефти в однородной полосообразной залежи неньютоновской нефти от контура питания до галереи.

Во второй задаче фильтрация несжимаемой неньютоновской нефти происходит с плоскорадиальным простым потоком.

На Рисунке 2 показана схема системы «скважина — круговая залежь», в котором представлены следующие условные обозначения: P k — пластовое давление, P c — динамическое забойное давление скважины, R — текущее давление, R k — радиус контура питания, r c — радиус скважины, r — текущий радиус вектор, h —мощность (толщина) продуктивного пласта.

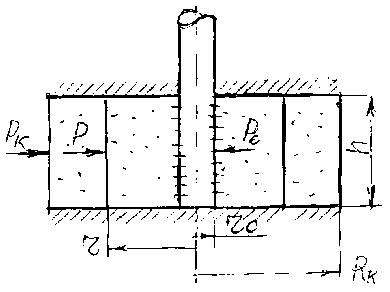
Рисунок 2. Схема системы «скважина — круговая залежь»

Процесс фильтрации происходит по Общему нелинейному закону, в виде:

u = Cк

dP) dr ;

Площадь текущей цилиндрической поверхности фильтрации, будет:

F = 2 n rh                                          (14)

Используя значения υ и F из формул (13) и (14), составляем следующее дифференциальное уравнение:

Q

= и • F = 2n hcrк

dP 1 dr у

n

Разделяя на переменные уравнение (15) и интегрируя его в пределах по P от P k до P c и по r от R k до r c , выводим формулу для дебита скважины, в виде:

Q = 2 n hC

(Pk - Pc )n

(Rk ■ - r-■ )(1 - n)

Текущая скорость фильтрации неньютоновской нефти, будет:

( Pk - P c ) ¹        1

---------------------- . —

( 1 - „ ) ( Rk ^- n - r- n ) ■  ^r

1 f Q

1 - n 1 2 n hC

'k - ■ - r^{1 -} ■ ) = P k - P

Подставляя значение Q из формулы (16), получаем следующий закон распределение текущего давления P в дренажной зоне круговой однородной залежи:

P = P - ^{( 1 -} ■ ^{)( P} k - ^P C ) . ( R I^- ■ - r 1- ■ ) ■                                         ⁽¹⁹⁾

k                              1 k

( R k ^- n - r C n ) ■

Дифференцируя P по r в формуле (19), получаем следующее выражение для текущего градиента давления:

dP  ( 1 - n X P k - P_c )   1

--- =--------------:— ■ -- dr    (R1 n - rCn)■   rn

А теперь определим частичную продолжительность продвижения этой нефти от текущего положения r до скважины:

c      ( Pk - Pc ) ¹       1     dr

— =--------------=-- m (1 - n)(R1 n - r-n)■  rn     dt

Разделяя на переменные дифференциальное уравнение (21) и решая его в пределах по t от нуля до t и по r от r до r c , частичная продолжительность продвижения нефти, получается, в виде:

m ( 1 - n ) ( Rk-ⁿ - rC-ⁿ ) ■ C ( Pk - Pc ) ⁿ

■^{( r 2 -} rc ^{) .}

При r=R k : t=T и имеем:

_T= m ( 1 - n X « Г ⁿ - rc " ) ⁿ c ( Pk - Pc ) ⁿ

■^{( R}k ^- rcc )

По формуле (23) определяется полная продолжительность продвижения нефти от контура питания до скважины.

В третьей задаче фильтрация нефти происходит с полусферическирадиальным простым потоком в пласте с большой мощностью.

А теперь интегрируем дифференциальное уравнение (15) в других пределах по P от P k

до P и по r от Rk до r: f _Q_ Xn]dL=PdP I 2nhcJ {rn   P и имеем:

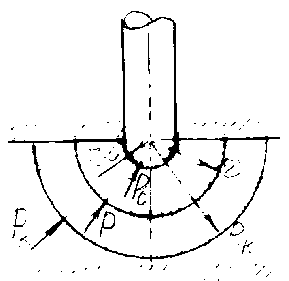
Рисунок 3. Схема системы «полусферическая залежь — скважина»

На Рисунке 3 представлена схема системы «скважина — полусферическирадиальная залежь», в котором представлены следующие условные обозначения: P k — пластовое давление, P c — динамическое забойное давление скважины, P — текущее давление, R k — радиус контура питания, r c — радиус скважины, r —текущий радиус-вектор.

Нелинейный закон фильтрации для полусферического простого потока тоже выражается по формуле (13). Площадь текущей полусферической поверхности фильтрации, будет:

F = 2 n r ² (24)

Используя значения υ и F из формул (13) и (24), получаем следующее дифференциальное уравнение:

n

Q = v F = 2nr2 ■ C — V dr J

Разделяя на переменные уравнение (25) и интегрируя в пределах по P от P k до P c и по r от R k до r c , выводим формулы дебита нефти скважины, в виде:

_{1                 n} ¹                                                        (26)

Q = 2 л- C ( 2 n + 1 ) n —P--C^

( R^{n + 1} - F_c^{n + 1} ) n

С учетом формул (24) и (26), получаем следующую формулу для текущей скорости фильтрации нефти в этой залежи:

_r (in + tFp - pF . i

^C                  \1      2

(R; ■+1 - rC ■+1)n     r

Интегрируя дифференциальное уравнение (25) в других пределах по r от R k до r и по P

от Pk до P: < Q AnR^dr   PkJ                                                    (28) V2nCJ rr=■ =¥Р получаем:

---- Q ---  ( R ■ + 1 - r ’ ■ + 1 ) ■ = ( p - P ) ¹ 2 n C ( 2 ■ + 1 ) ■

Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №2. 2022 0.336 9/24 4-2948/75

Подставляя значение Q из формулы (26) в формуле (29), получаем следующий закон распределения текущего давления в дренажной зоне залежи:

P=Pk

—

P k

—

P C

2 n + 1

Rk

2 n + 1

— Г

rC

( R ' ' '

2 n + 1

—r )

Дифференцируя P по r в формуле (30), получаем формулу текущего градиента давления:

dP  (Pk— Pc X2 n ' ')  ,

— =--r dr       Rk2 n'' — r22 n''

Частичная продолжительность продвижения нефти в пласте от текущего положения r до скважины найдена, в виде:

t =

2 n + '        2 n + '

m ^{( R},   ^{— r}c  ) n

3 C ( 2 n ' ' ) n ( P , — P c ) n

•(Rk — r3)

При r = 0: t = T и имеем:

T =

m (Rk—'— rC—')n 3C(2n ' ')n (P, — Pc )i

• R,

По формуле (33) определяется полная продолжительность продвинется нефти в дренажной зоне полусферическирадиальной залежи от контура питания до скважины.

Выводы и рекомендации

Решены три стационарной гидростатической задачи, в которых процессы фильтрации подчиняются только Общему нелинейному закону. В задачах происходят простые потоки фильтрации: плоскопараллельная, плоскорадиальная и полусферическирадиальная.

Выведены во всех задачах все основные расчетные формулы характеризующие процессы фильтрации: дебиты, скорости фильтрации, градиента давления и т. д. Эти формулы нужно использовать при решении различных практических задач разработки залежей неньютоновской нефти, а также при составлении проекта разработки нового разведанного месторождения. Анализируя выведенные формулы можно выявить специфические особенности разработки подобных залежей, разработать и внедрять необходимые мероприятия по предупреждению и устранению нежелательных явлений.