Протекание через фрактальную пористую среду

Заметим, что наличие базы данных моделей типичных инженерных поверхностей после того или иного вида обработки позволяет провести компьютерное моделирование стыка и оценить порог герметичности с учетом направления следов обработки соприкасающихся поверхностей.

Для фрактальной пористой среды (Пуазейль) расход может быть записан в виде q r p GC ФAp.

l n

Здесь r – радиус поры; l – длина поры; η – динамическая вязкость; Δp – перепад давления (напор).

Представляя фрактальную пористую среду в виде набора пор, имеющих определенную плотность распределения их размеров, полагаем, что радиус поры примерно равен ее длине ( r ≈ l ).

Обозначим проницаемость и порог проницаемости соответственно через Ф и Ф с (наименьшее значение проницаемости в бесконечном кластере пор). Вероятность протекания через пору – W ( Ф ).

Тогда порог протекания (концентрация пор, приводящая к формированию цепочки связанных между собой пор, через которую происходит утечка) опре- деляется формулой p = J W Ф dФ.

c _Ф

c

Плотность распределения пор [2] по радиусам r 2D представим в виде W r 3 D

r max

Здесь D – фрактальная размерность (1< D <2); r max – радиус наибольшей поры.

Представление пористой среды в виде набора пор сферической формы является частным случаем набора вытянутых пор (в виде цилиндрических трубок). Пусть трубки имеют радиус r и длину С∙r. Тогда объем трубки равен V= πr ² C∙r=Cπr³. Для пор сферической формы объем V=(4/3) πr ³.

В этой модели [3] плотность распределения пор определяется зависимостью

1 D

Wr 3 D ^r 3 D .

^С•7t-r max

Вероятность нахождения трубки радиуса r равна

W r dr осr1D

или

1 D

W r dr 3 D ^r       dr .

С • ТЕ •  3D rmax

Пористость определим из соотношения

Г max m= J W r Vdr г rmin

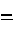
r max                ^{1 D}

' x3DСr r3 D rmin                rmax

C • ТЕ •r ³ dr .

Интегрируя это выражение, найдем m1

3D г • rmin

Г

V r max 7

Связь между пористостью и фрактальной раз- мерностью определяется выражением

D 3 ^{lg 1 m}             (1)

lg r / г g min max

Обычно при определении пористости учитывают только связанные между собой поры и не учитывают изолированные поры, не участвующие в перемещении уплотняемой среды внутри пористой среды.

Используя фрактальные представления, используемые в работе [4], пористость может быть опреде- iD E лена из соотношения:    m 1 b    .

где b, i – коэффициенты; D – фрактальная размерность профиля зазора (1< D <2); Е – эвклидова размерность ( Е =2).

Фрактальная размерность в этом случае будет lg 1 m равна         DgmE        (2)

i lg b

В соответствии с 2- D перколяционной моделью, рассматривающей протекание по узлам (порам) на квадратной решетке, просачивание наступает тогда, когда цепочка пор достигает противоположной стороны по наименьшему пути.

Расположение пор (белые клетки на рис. 1) формируется с помощью распределения Бернулли. Остальные черные клетки указывают на отсутствие пор и невозможность протекания через них.

Проведенные многими исследователями численные эксперименты показали, что протекание наступает при концентрации пор (отношение числа пор к общему числу клеток, равному, например 70х70), оцениваемой величиной

p _c

п пор

.

n _о

Здесь n пор – количество пор; n о – общее число клеток квадратной решетки.

Анализ рис. 1 показывает, что при малой концентрации пор, не достигшей порогового значения, протекание невозможно, а при превышении порогового значения наблюдается протекание.

Пороговое значение концентрации:

• •    для 2- D перколяционной модели р с =0,5927;

• •    для 3- D модели концентрация пор р с =0,3116.

  

  Рис. 1. Заполнение квадратной решетки порами (белые квадраты):а) концентрация пор р =0,21б) концентрация пор р =0,73.

  
  

На рис. 2 представлен канал протекания в трёхмерном пористом слое, смоделированном с вероятностью заполнения 65% непроницаемыми кубами, при этом независимый сквозной канал один длиной 115 кубов при длине пористого слоя в 50 кубов. Однако эти теоретические модели не рассматривают анизотропию или негомогенность пористой структуры и пористость разного масштаба измерения.

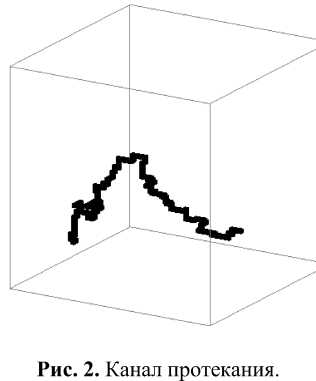
3- D модель требует сравнения с реальными процессами протекания (фильтрации) в пористой среде (через межконтактный зазор инженерных металл-металлических поверхностей. Фрактальные представления о пористой среде позволяют дать более точные количественные оценки параметров, входящих в исходное уравнение А. Дарси.

Согласно абстрактным 2-D и 3-D моделям предполагается, что пористость численно равна критическому значению концентрации пор, при которой осуществляется переход от состояния герметичности к протеканию m=pc.

Так, для 2- D модели при b =3; i =1 фрактальная размерность пористого слоя при m =0,5927 определяется по формуле

_D lg 1 m _E i lg b lg 1  0,5927    _{2  1,182.}

1 lg 3

Для 3- D модели при b =3; i =1 фрактальная размерность пористого слоя при m =0,3116 равна

D lg 1 m E i lg b lg 1  0,3116

=--1- 3 = 2,662.

1 lg 3

Сравним полученную оценку фрактальной размерности с расчетом по формуле (1). При отношении r_max/r_min =3 и m =0,3116 найдем D =2.66.

При малых значениях соотношения (rmin / rmax)3-D , где rmin=rc - критическая величина радиуса поры, ниже которой просачивание невозможно, справед-3D г min

1   m .

ливо выражение

г

max /

Тогда отношение гс / rmax имеет вид r              1  3D с 1m         .

г

max

Отношение г с / r_max зависит от пористости и фрактальной размерности (критическое значение радиуса изменяется в пределах [3] от r c =r_max /5 до r c =r max /2). Отметим, что минимальный радиус поры, через которую еще возможно просачивание, является для рассматриваемого конкретного случая постоянной величиной. Минимальный (критический) радиус поры, в свою очередь, зависит от многих факторов: вязкости, числа Рейнольдса, наличия граничного слоя прилипших к стенкам поры молекул уплотняемой среды и др.

В ряде случаев удается установить связь между пористостью и фрактальной размерностью, которую можно записать в первом приближении в виде как m = 3- D, 2< D <3.

Зависимость отношения r min / r_max от фрактальной размерности D представлена на рис.3.

Полученные данные о фрактальной размерности можно считать предварительными. Окончательную оценку фрактальной размерности и пористости (межконтактного зазора) дадим с помощью компью- терного моделирования.

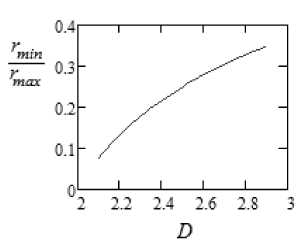
Рис. 3. Зависимость отношения r_min / r_max от фрактальной размерности D.

Для анализа профиля зазоров при контакте двух шероховатых поверхностей использовалось разработанное нами программное обеспечение. В качестве исходных данных использовались трёхмерные карты реальных поверхностей и их моделей с разными микрогеометрическими параметрами. Пример изотропных поверхностей с разной фрактальной размерностью, используемых при моделировании, представлен на рис. 4.

В разработанной нами программе две поверхности приводятся в контакт, образуя межконтактный зазор. Все основные параметры, такие, как величина зазора, сближение, площадь контакта, пористость и т.д. отображаются в окне программы (рис. 5).

Рис. 4. Поверхности 3-D: а - модель, б - реальная поверхность.

Основной функцией данной разработки является моделирование протекания жидкой среды через стык поверхностей с возможностью сближения. Поверхности сближаются с учётом расплющивания микровыступов и их взаимного внедрения друг в друга. Для упрощения модели материалы двух сопряжённых поверхностей считаются одинаковыми. Сближение поверхностей автоматически продолжается до момента, когда протекание жидкости в направлении сверху вниз становится невозможным -наступает полная герметичность.

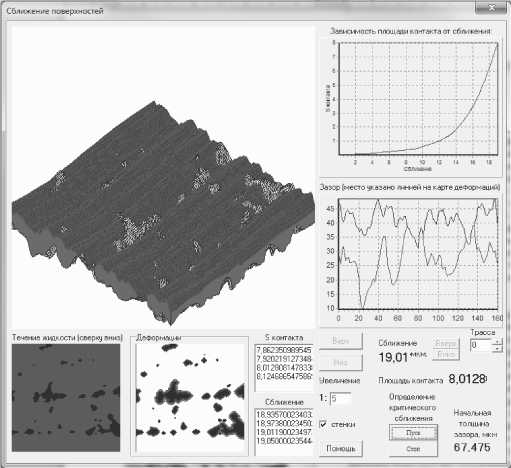
Рис. 5. Моделирование контакта поверхностей.

Картина распределения пор, пятен касания и каналов представлена на рис. 6. Эта картина меняется при увеличении сближения. В этом случае площадь, занятая металлическим контактом, растет.

Таким образом, существующие модели протекания (фильтрационная - Дарси, капиллярная – Гаге-на-Пуазейля, щелевая) содержат для согласования с экспериментальными данными ряд коэффициентов, которые в ряде случаев либо трудно определить, либо принимаемые в расчетах значения недостаточно обоснованы.

Нами предложена фрактальная модель, позволяющая оценить протекание (просачивание) через соединение инженерных поверхностей. Модель рассматривает просачивание через фрактальную пористую среду, которая в самом общем виде представляет собой выделенный герметизирующий объем, содержащий систему пор, имеющих определенное распределение размеров этих пор и их концентрацию.

Важными параметрами являются фрактальная размерность пористой среды и концентрация, при которой формируется бесконечный кластер – цепочка пор, по которой происходит утечка. При этом важно выделить критический размер поры, размеры которой делают невозможным протекание через эту пору.

Фрактальная модель позволяет рассматривать пористость на разных масштабных уровнях. Так, для стыка мультифрактальных поверхностей пористость равна сумме, определяющей раздельно особенности пористого слоя на разных уровнях m=ms + mt,

3         ^r s max

S2

Здесь m         S       rS

г smax s m in

б

в

Рис. 6. Картина зазора между шероховатыми поверхностями приразличном сближении (а - 7 мкм, б - 20 мкм, с - 27 мкм; светлые пятна – поры, темные – площадки металлического контакта, серые – капилляры).

m _t

3 D  rt m ax t-     f   rt2

г.

tmax rt m in

Дополнительным условием подобного разделения является следующее утверждение: радиус САмой наименьшей «структурной» поры всегда больше радиуса самой большой «текстурной» поры.

Для определения пористости необходимо определить фрактальные размерности этих особенностей пористой среды.

Итак, фрактальная модель в определенной степени объединяет фильтрационную и капиллярную модели, при этом капилляр представляет собой пору, имеющую равные размеры радиуса и длины или пору цилиндрической формы, у которой длина существенно больше радиуса. Точные значения порога протекания и необходимые закономерности, оценивающие утечку через пористую среду, рассматриваются с помощью компьютерного моделирования.