Противостояние
Автор: Соловьв А.С.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Основной раздел
Статья в выпуске: 10 (65), 2019 года.
Бесплатный доступ
В работе предлагается метод оценки двух систем, находящихся в бинарном отношении качественного порядка. Материал представлен в изложении Notebook MATLAB.
Короткий адрес: https://sciup.org/140245946
IDR: 140245946 | УДК: 330.1(0.75.8),
Текст научной статьи Противостояние
Рассматриваем две системы X и Y , две системы взглядов на одну и ту же проблему, например, преподавателя и студента на оценку знания разделов курса с бальной оцифровкой по одной и той же шкале. Очевидно, системы оценки будут различаться. Каждый из них имеет свой взгляд на проблему и выбирает свою стратегию поведения. Обозначим X систему оценки взгляда студента, а оценку преподавателя - Y . Примем взгляды преподавателя за эталон. Пусть данные оцифрованные бальные оценки имеют вид
X= [5 3 2 0 0 0 0 0; 0 0 0 3 2 1 0 0 ; 0 0 0 0 0 0 2 5;2 2 3 5 0 0 0 0; 0 1 0 0 0 0 3 7;
|
6 7 4 0 0 0 0 0; 0 0 0 4 2 3 0 |
0; 4 3 2 0 0 0 0 0; 0 0 0 5 6 3 0 0; 0 1 0 0 0 0 3 7] |
||||||
|
Y = [5 4 3 0 0 0 0 0; 0 0 0 2 6 7 5 6; 6 5 4 1 0 0 0 0; 0 0 0 1 5 8 6 7; |
|||||||
|
0 0 1 7 8 0 0 0; 4 3 2 0 0 0 0 0; 0 0 0 8 7 1 0 0] |
|||||||
|
X = 5 |
3 |
2 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
3 |
2 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
2 |
5 |
|
2 |
2 |
3 |
5 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
3 |
7 |
|
6 |
7 |
4 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
4 |
2 |
3 |
0 |
0 |
|
4 |
3 |
2 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
5 |
6 |
3 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
3 |
7 |
|
Y = 5 |
4 |
3 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
2 |
6 |
7 |
5 |
6 |
|
6 |
5 |
4 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
5 |
8 |
6 |
7 |
|
0 |
0 |
1 |
7 |
8 |
0 |
0 |
0 |
Видим, что системы описываются в одном и том же факторном пространстве ℝ8 и являются двумерными массивами, но матрицы не являются квадратными. На практике возможна ситуация, когда состояние каждой системы описывается в своём пространстве факторов многомерными массивами как, например, в работе [1].
На высшем агрегатном уровне любая оценка бинарного сопоставления систем X и Y имеет две стороны: внешнюю количественную объёмную скалярную величину u(X, Y), и внутреннюю качественную дифференциальную векторную v(X, Y) [2]. Пусть объёмная характеристика строится по отношению возможностей работы. Поскольку пространство и время разделяются условно объёмную характеристику определим как мощность u (работа в условную единицу времени), количественная бальная оценка необходимого багажа знаний студента. Мощность будет количественной скалярной характеристикой наблюдаемой системы. Оценке мощности в соответствие можно поставить такую физическую характеристику как яркость света [3, стр.70].
Будем полагать, что системы взглядов субъектов X и Y в пространстве ^тхп согласованны. Тогда для норм матриц оцифровки курса, подчинённых соответствующим нормам их элементов, справедливо свойство субмультипликативности
im < ||х|||и|-
При введении обозначений
D(X) = ||X||2, D(Y) = ||Y||2, mx, Y)i = ^wW+Tiw2^ приходим к основному метрическому тождеству D(X)D(Y) = u2(X, Y) + |r(X,Y)|2, которое после деления на множитель D(X) принимает вид D(X) = Ey2(X) + IV(X), где выражение EY(X) интерпретируется как математическое ожидание свойств системы Y в состоянии системы X, а VY(X) – показатель дисперсии этих ожиданий. Здесь u(X, Y) положительная симметричная билинейная форма, порождаемая функционалом D(X). Так как система Y принята в качестве эталона, то можно найти шанс обнаружить свойства эталона в состоянии системы X ChanceY(X') = Ey2(X) Vy(.X) . В данном случае построение внутреннего произведения опирается на определение нормы матрицы, которая имеет различные представления [4]. Если матрицы одного и того же порядка, т.е. X, Y Е ^тхп, то анализ их бинарного соответствия можно проводить на паре (X • Y, X Л Y) в композиционной алгебре с делением над полем действительных чисел [5]. Однако более простым и информативным будет анализ, построенный на усреднённом представлении о состоянии системы с поэлементным сопоставлением. Полагая, что системы строят свои оценки по своему среднему состоянию (не экстремальному, уравновешенному), вычислим их средние характеристики. Это будут векторы x = mean(X), y = mean(Y) x = 1.7000 1.7000 1.1000 1.7000 1.0000 0.7000 0.8000 y = 2.1429 1.7143 1.4286 2.7143 3.7143 2.2857 1.5714 Нормируем эти векторы х у ХХ sqrt(x*x'y ^у sqrt(y*y')' Nx = 0.4301 0.4301 0.2783 0.4301 0.2530 0.1771 0.2024 Ny = 0.3311 0.2649 0.2208 0.4194 0.5740 0.3532 0.2428 1.9000 1.8571 0.4807 0.2870 Тогда мощность любого объекта z агрегатного свойства системы X будет равна системы XU Y по отношению Zk i PjZJ, pj =x0 = J=i xJ ^О(х) Zk J=1 pJ =1 Свою мощность система X оценивает величиной Zm m~*my-! Ex (xt) = ) ) i=i z—ii=iZ_i i J=i PjxJ. Мощность противоположной системы – величиной Zm у—il 1=14—IJ pjyJ. Применяя алгоритм for k = 1:size(X,1) EXx(k,1) = X(k,:)*Nx'; end for k = 1:size(X,1) EXy(k,1) = X(k,:)*Ny'; end for k = 1:size(Y,1) EYx(k,1) = Y(k,:)*Nx'; end for k = 1:size(Y,1) EYy(k,1) = Y(k,:)*Ny'; end uEX = [EXx EXy], uEY =[EYx EYy] находим оценки мощности системы X и системы Y uEX = 3.9978 2.8919 1.9736 2.7594 2.8086 1.9206 4.7062 3.9515 4.4026 3.0023 6.7051 4.7242 2.7579 3.8853 3.5676 2.5608 4.2002 6.6006 4.4026 3.0023 uEY = 4.7062 3.3776 7.5148 9.6912 6.2750 4.6138 7.6919 9.5808 5.3135 7.7485 3.5676 2.5608 5.3894 7.7264 Находим оценки каждой системы суммарной мощности SuEX = sum(uEX), SuEY = sum(uEY) SuEX = 39.5221 35.2988 SuEY = 40.4583 45.2990 Видим, что по мощности системы Y превосходит мощность системы X как, по своей оценке, так и в оценках противоположной системы, но каждая система оценивает себя выше соперника. Качественное расхождение систем можно оценить показателем вероятности их сходства p = (Nx • Ny)2, p = (Nx*Ny)^2 p = 0.7977, который отвечает показателю вращательной симметрии в угловом измерении кватернионного представления оценки бинарного сходства рассматриваемых состояний 6 = arccos(^p) = 0.4665 (рад) = 26.73 (град.) Системы практически качественно подобны, поэтому шанс обнаружить, например, знания студентом соответствующего курса преподавателем удовлетворителен (1 :4): p Chancey (X) = —^— = 3.94.
1 — p Агрегированное качество каждого объекта в оценках самой системы и противоположной найдём, если каждый вектор соответствующего объекта нормировать и умножить на соответствующий вектор средних. for k = 1:size(X,1) NXX(k,:) = (X(k,:)/sqrt(X(k,:)*X(k,:)'))*Nx'; end for k = 1:size(X,1) NXY(k,:) = (X(k,:)/sqrt(X(k,:)*X(k,:)'))*Ny'; end qNX = [EXx EXy NXX NXY] qNX = 3.9978 2.8919 0.6485 0.4691 1.9736 2.7594 0.5275 0.7375 2.8086 1.9206 0.5215 0.3566 4.7062 3.9515 0.7262 0.6097 4.4026 3.0023 0.5732 0.3909 6.7051 4.7242 0.6672 0.4701 2.7579 3.8853 0.5121 0.7215 3.5676 2.5608 0.6625 0.4755 4.2002 6.6006 0.5020 0.7889 4.4026 3.0023 0.5732 0.3909 Находим математические ожидания оценки системы X преподавателем и студентом EX =[EXx EXy], sumEX = sum(EX), Tab1 = [EX; sumEX] NX = [NXX NXY], meanNX = mean(NX), Tab2 = [NX; meanNX] Tab = [Tab1 Tab2] Результаты расчётов оценки системой Y элементов системы X по мощности и качеству приведены в табл. 1. Таблица 1. Оценка системы X Оценка мощности Оценка качества По среднему системы X По эталону Y По среднему X По эталону Y 1. 4.00 2.89 0.65 0.47 2. 1.97 2.76 0.53 0.74 3. 2.81 1.92 0.52 0.36 й о ь« Ю О 4. 4.71 3.95 0.73 0.61 5. 4.40 3.00 0.57 0.39 6. 6.71 4.72 0.67 0.47 7. 2.76 3.89 0.51 0.72 8. 3.57 2.56 0.66 0.48 9. 4.20 6.60 0.50 0.79 10. 4.40 3.00 0.57 0.39 Показатели Суммарные показатели Средние показатели качества системы 39.52 35.30 0.59 0.54 По мощности объекты могут разбиты на классы. Разобьём их на три класса. Для этого дисперсионный интервал мощности разделим на три равных интервала. Определим интервал вариации мощности и найдём его треть длины a = min(EXy), b = max(EXy), d = (b – a)/3; a1 = a+d, a2 = a1 + d a = 1.92, b = 6.60, a1 = 3.48, a2 = 5.04 Найдём интервалы расслоения объектов по мощности disp([' [a, a1) = [' num2str(a) ', ' num2str(a1) ')']) disp([' [a1, a2) = [' num2str(a1) ', ' num2str(a2) ')']) disp([' [a2, b) = [' num2str(a2) ', ' num2str(b) ']']) [a, a1) = [1.9206, 3.4806) [a1, a2) = [3.4806, 5.0406) [a2, b) = [5.0406, 6.6006] Получим оценку преподавателем знаний студента по их объёмным характеристикам как групповое разбиение G1 = {1, 2, 3, 5, 8, 10}, G2 = {4, 6, 7}, G3 = {9} с упорядочиванием G1 < G2 < G3. Таким образом, студент в достаточном объёме не владеет большинством тем. На среднем уровне постиг объёмы разделов 4, 6, и 7. И в полном объёме проработал тему 9. Для разбиения системы X по качественным кластерам нормируем её объекты for k = 1 : size(X,1) NormX(k,:) = X(k,:)/sqrt(X(k,:)*X(k,:)'); end присоединяем к полученной матрице снизу строку, равную нормированному среднему системы Y NormXNy = [NormX Ny] и строим корреляционную и вариационную матрицы for k = 1:size(NormXNy,1) for l = 1:size(NormXNy,1) corNXy(k,l) = NormXNy(k,:) *NormXNy(l,:)'; end end corNXy, varNXy = sqrt(1 – corNXy.^2) Корреляционная матрица показывает близость качественного сходства знаний тем студентом в оценке преподавателя. Если воспользоваться алгоритмом L = .6 F = corNXy; [ g ] = ClassF( F, L) for i=1:size(F,1) for j=2:size(F,1) if F(i,j) > L S(i,j) = 1; S(j,i) = 1; else S(i,j) = 0; S(j,i) = 0; end end S(i,i) = 1; end g = symrcm(S); R=S(g,g); subplot(1,2,1), spy(S); subplot(1,2,2),spy(R) построенным на методе Даймейджа-Мендельсона, то на уровне шестидесятипроцентной корреляции объекты системы X по качеству – глубине проработки материала курса, расслаиваются на три класса K1 = {8, 1 6}, K2 = {4, 2, 9, 7}, K3 = {10, 3, 5}, рис. 1. 0 5 10 nz = 39 0 5 10 nz = 39 Рис. 1 Расслоение объектов системы X по качеству системы Y. Количественные показатели – показатели мощности, являются линейно квантованными (отметим, что внутри приведённых выше групп порядок не устанавливается), качественные же классы квантуются циклически. Из таб. 1 находим их следование по глубине проработки материала курса: К3Ж1> К2. Наименее проработанным материалом будет пересечение кластеров G1 и K3. Наиболее проработанным материалом будет пересечение кластеров G3 и K2: G1∩K3 = {1, 2, 6, 10}∩{10, 3, 5} = {10}, G3∩k2 = {7, 8}∩{4, 2, 9, 7} = {7}. В заключение отметим, что работа написана в Notebook MATLAB и алгоритм решения можно использовать для решения аналогичных и более ёмких задач.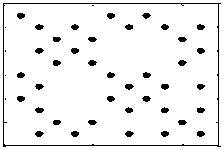
Список литературы Противостояние
- Соловьёв А.С. Региональные банки на пиках инфляции //ж. "Экономика и социум" №12(55), 2018. www.iupr.ru
- Идлис Г.М. Единство естествознания по Бору и единообразные взаимосвязанные периодические системы физики, химии, биологии и психологии /Исследования по физики и механики, 1990 //М., Наука, 1990.
- Фор А. Восприятие и распознавание образов //М., Машиностроение, 1989.
- https://ru.wikipedia.org/wiki/%D0%9D%D0%BE%D1%80%D0%BC%D0%B0_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D1%8B
- https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D1%86%D0%B5%D0%B4%D1%83%D1%80%D0%B0_%D0%9A%D1%8D%D0%BB%D0%B8_%E2%80%94_%D0%94%D0%B8%D0%BA%D1%81%D0%BE%D0%BD%D0%B0


