Проверка нормальности распределения значений держащей силы якоря

В результате исследований, как правило, получают большое количество однотипных значений наблюдаемой̆ величины. Все эти значения называют статистической̆ совокупностью. Генеральная статистическая совокупность содержит в себе все возможные значения случайных чисел. В большинстве случаев при исследованиях получают так называемую выборочную совокупность, в которой̆ содержится лишь некоторая часть случайных чисел генеральной̆ совокупности. Выборочную совокупность называют выборкой̆, а число экспериментов в выборке – объемом выборки. При планировании и проведении экспериментов в большинстве случаев создаются подобные условия. При этом появляется закономерность в частоте появления результатов опытов.

Наиболее мощным программным обеспечением (ПО) для обработки статистических данных является Statistica. Большое количество литературных источников [1] наглядно показывают, как можно пользоваться данным программным комплексом.

В работе рассмотрен подбор закона распределения значений держащей силы с помощью ПО Statistica. Чтобы установить, по какому закону распределены значения случайных величин, необходимо воспользоваться программным модулем Distribution fitting, позволяющим определить соответствие анализируемых данных ряду математических распределений.

Variable: Var1, Distribution: Normal

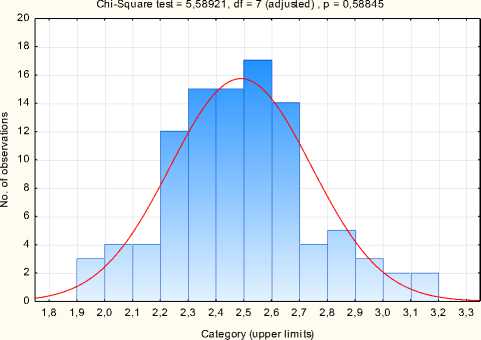
Рисунок 1.10 График наблюдаемого и ожидаемого распределения

Визуально по построенному графику (рис. 1.10) можно сделать вывод о том, что случайные значения наблюдаемой величины подвержены нормальному закону распределения. Выдвинем гипотезу о том, что имеющиеся эмпирические данные подчиняются нормальному закону распределения.

Для проверки гипотезы о том, что эмпирическое распределение случайной величины соответствует теоретическому распределению вероятностей, используют критерии согласия.

Существует большое количество критериев согласия, наиболее распространенными из которых являются: критерий Пирсона (χ2), критерий Колмогорова (Колмогорова–Смирнова).

• 1.    Критерий Пирсона (χ2). Наиболее часто употребляемый̆ критерий при достаточном объеме выборки (n > 100) для проверки гипотезы о принадлежности наблюдаемой̆ выборки случайной̆ величины теоретическому закону распределения. Его можно представить, как сумму отношений квадратов расхождений между теоретическими и эмпирическими частотами к теоретическим частотам.

• 2.    Критерий Колмогорова (Колмогорова–Смирнова). Предназначен для проверки гипотезы о принадлежности выборки случайных чисел определенному закону распределения.

Основан на определении максимального расхождения между накопленными эмпирическими и теоретическими частотами.

Одним из основных условий использования критерия Колмогорова, является достаточно большое число наблюдений.

• В    некоторых случаях мощность теста χ ² (критерий Пирсона) при проверке нормальности распределения случайной величины относительно невысока. Поэтому можно воспользоваться другими критериями согласия, например, Колмогорова – Смирнова и Шапиро – Уилка.

Для определения распределения случайной величины в ПО Statistica построена гистограмма, на которой указаны два критерия согласия (рис.1.11).

Histogram: Var1

K-S d=,05864, p> .20; Lilliefors p> .20

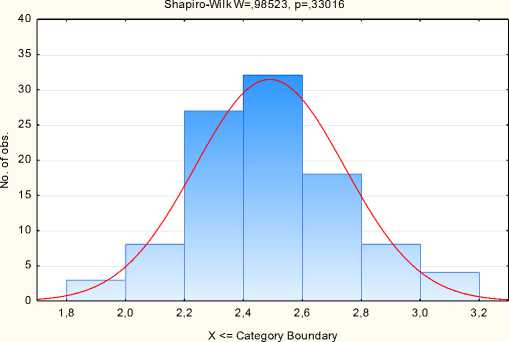
Рисунок 1.11 Проверка нормальности распределения с помощью критериев согласия Колмогорова – Смирного и Шапиро – Уилка

Проанализируем данные, полученные при построении гистограммы. По критерию согласия Колмогорова–Смирнова (K–S на рис.1.11) можно сделать вывод, что уровень значимости (p) больше 0,2, следовательно, гипотеза о нормальности имеющегося распределения случайной̆ величины не отклоняется. По Шапиро–Уилка (Shapiro-Wilk на рис.1.11) уровень значимости больше 0,05, следовательно, гипотеза о нормальности имеющегося распределения случайной величины не отклоняется.

Кроме критериев согласия на нормальность распределения могут указать и описательные статистики. Полученные описательные статистики для выборки представлены на рисунке 1.12.

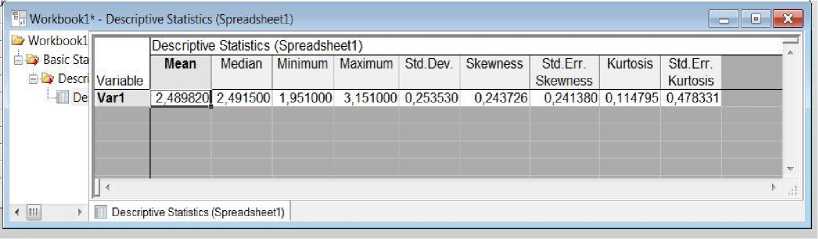
Рисунок 1.12 Описательные статистики для выборки

Проведем анализ полученных статистик.

• 1.    Среднее значение (mean) и медиана (median) близки по своим значениям. Это является одним из косвенных признаков нормальности распределения.

• 2.    Оценим коэффициент асимметрии (skewness). Его величина может быть положительной̆ (для правосторонней̆ асимметрии) и отрицательной̆ (для левосторонней̆ асимметрии). Если асимметрия по модулю выше 0,5, то она считается значительной̆. Если значение коэффициента асимметрии более чем в 2 раза превышает стандартную ошибку асимметрии (std. err. skewness), то это указывает на наличие асимметрии распределения. По рисунку 1.12 можно сделать вывод, что асимметрия незначительна и гипотеза о нормальности распределения не отклоняется.

• 3.    Оценим значение эксцесса (kurtosis). Если его значение больше нуля, то график распределения случайной̆ величины будет островершинным, в обратном случае – плосковершинным. Для нормального распределения значение эксцесса должно быть близко к 0.

Если значения эксцесса и его стандартной̆ ошибки (std. err. kurtosis) различаются по модулю менее, чем в 2 раза, то это является одним из косвенных признаков нормальности распределения. По рисунку 1.12. можно сделать вывод, что значения эксцесса и его стандартной̆ ошибки различаются по модулю более, чем в 4 раза, следовательно, гипотеза о нормальности распределения отклоняется.

Полученный нормально-вероятностный̆ график представлен на рисунке 1.13.

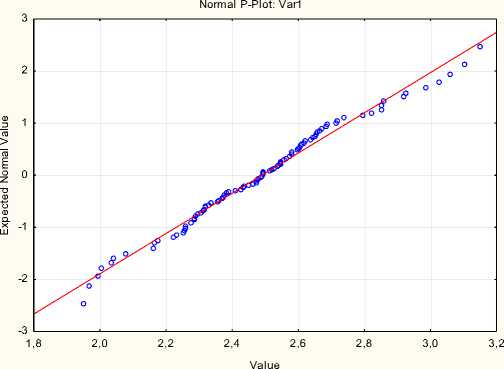
Рисунок 1.13 Нормально-вероятностный график

В том случае, когда экспериментальные данные достаточно близко расположены вдоль теоретической нормальной прямой (рисунок 1.13), гипотеза о нормальности не отклоняется.

Нормальность распределения случайной величины также может быть оценена с помощью «ящичной̆» диаграммы (BoxPlot). В ПО «Statistica» данный тип диаграммы получают в модуле Graphs. Выбираем 2D и диаграмму BoxPlot (рисунок 1.14).

Box Plot of Var1

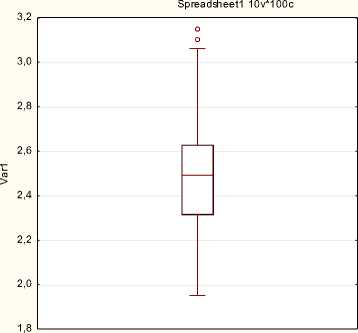
Median = 2,4915 □ 25%-75%

= (2,3135, 2,629)

J Non-Outlier Range

= (1,951, 3,061)

о Outliers

Extremes

Рисунок 1.14 Диаграмма Box Plot

Диаграмму Box plot можно оценить визуально: усы достаточно симметричны, медиана находится практически по центру, в целом распределение можно считать нормальным. В верхней части диаграммы видны две точки, которые говорят о наличии грубых ошибок. При наведении курсора на данные точки можно увидеть значение грубой ошибки. Исключим их из выборки и проверим ее на «нормальность».

Определим новые значения критериев согласия Колмогорова– Смирнова и Шапиро–Уилка

Histogram: Var1

K-S d=,04658, p> .20; Lilliefors p> .20

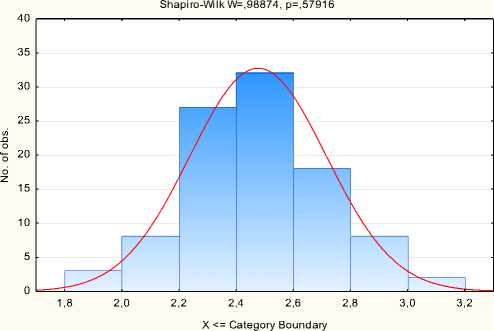
Рисунок 1.15 Проверка нормальности распределения

По критерию согласия Колмогорова–Смирнова уровень значимости больше 0,2, по Шапиро–Уилка – больше 0,05, следовательно, гипотеза о нормальности имеющегося распределения случайной величины не отклоняется. По сравнению с рис. 1.11 вероятность того, что распределение случайной величины близко к нормальному, стала выше.

Построим и проанализируем нормально-вероятностный график (рис. 1.17).

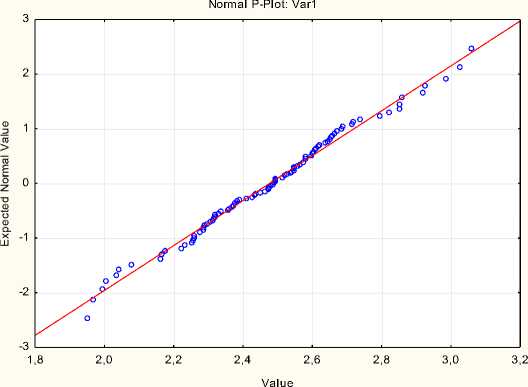
Рисунок 1.17 Нормально-вероятностный график

Экспериментальные данные достаточно близко расположены вдоль теоретической нормальной прямой, гипотеза о нормальности не отклоняется.

По сравнению с рис. 1.13 экспериментальные данные на графике (рис. 1.17)

находятся ближе к теоретической нормальной прямой.

Построим и проанализируем диаграмму BoxPlot (рис.1.18).

Box Plot of Var1

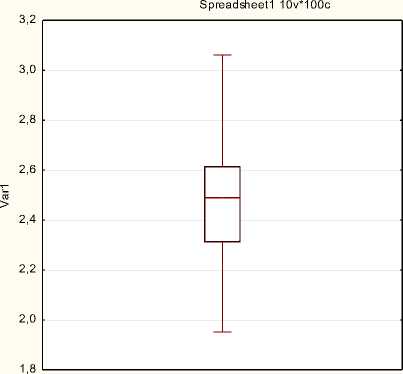
Median = 2,489

□ 25%-75%

= (2,312, 2,616)

I Non-Outlier Range

= (1,951, 3,061)

о Outliers

* Extremes

Рисунок 1.18 Диаграмма Box Plot

Ящик и усы достаточно симметричны, медиана находится практически по центру. Распределение случайной величины в выборке можно считать нормальным.

По сравнению с рис. 1.14 диаграмма (рис. 1.18) визуально выглядит более приближённой к описанию нормального распределения. Исключенные грубые ошибки из выборки отсутствуют.

В результате исследований теория о нормальности распределения значений держащей силы подтверждена.