Проверка теоретического решения по построению линии влияния вертикальных перемещений в трехшарнирной арке численным методом

Нами в работе [2] получено теоретическое решение по построению линии влияния вертикальных перемещений в произвольном сечении трехшарнирной арки. Произведем проверку правильности полученных формул двумя способами:

технических наук,

• —    с помощью вычисления интеграла Мора методом Верещагина на основе единичных эпюр изгибающих моментов Мк и М_п (рис. 1^ е);

• —    при помощи программы Lira 9.

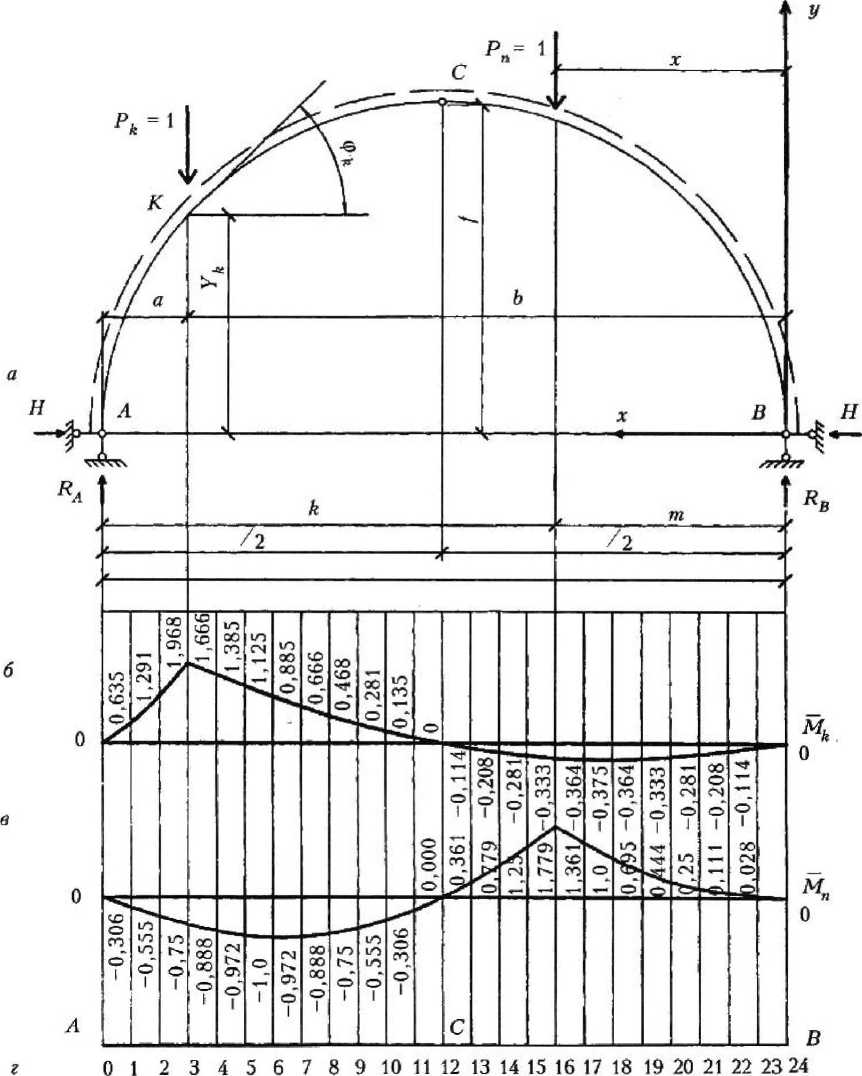
Рис. 1. Расчетные схемы; а — исходная расчетная схема трехшарнирной арки для определения усилий 0 <  х < I / 2 ; 6 — эпюра моментов Мк от действия единичной силы Р^ = 1, приложенной в сечении К, в — эпюра моментов М_п от действия единичной силы Р„ = 1, приложенной в сечении п на расстоянии 8 и от правой опоры В; г — номера характерных сечений арки

Единичные эпюры Мп и Ми были разбиты на 4 участка и от трех положений единичной силы Рп вычислены перемещения 5кп. Затем для уточнения этого решения те же эпюры мп и Мк были разбиты на 24 участка и методом Верещагина определены перемещения вышеуказанной точки.

Далее был проведен численный эксперимент с использованием программы Lira 9. По его результатам построена линия влияния вертикального перемещения сечения К арки (рис. 2). Все полученные параметры сведены в табл. 1.

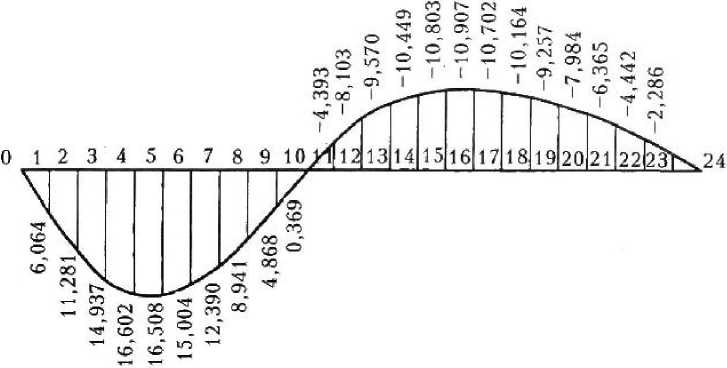
Рис. 2. Линия влияния вертикальных перемещений сечения К трехшарнирной арки от действия единичной силы P_r = 1, построенной по результатам программы Lira 9

д<                                          Таблица 1

Номер точки	Результаты по формуле трапеции		Lira 9	Метод непосредственного интегрирования
	в 1-м приближении	во 2-м приближении
2	10,172	9,68	11,281	9,21
5	16,833	15,95	16,508	15,61
16	-10,265	-10,732	-10,907	-9,21

Определим перемещения сечения К от действия единичной силы, приложенной в точке 2 (х = 22, у = 1,833), находящейся между крайней левой опорой и сечением К; в точке 5 (л ~ 19, у = 3,958), расположенной между сечением К и ключевым шарниром С; в точке 16 (х = 8, у = 5,333) — между ключевым шарниром С и крайней правой опорой. Для этого вычислим характерные значения эпюры Мк и М_п по аналитическим формулам, приведенным в [2] (см. рис. 16, у).

Найдем указанное перемещение в точке 16, расположенной на расстоянии 8 м от крайней правой опоры и на 4 м правее ключевого шарнира С.

Согласно формуле трапеции умножим эпюру Мк (см. рис. 16) на эпюру М_п (см. рис. Iff).

— dx =

-—■——(2 * сш- + 2 ■ bb_x + 6 ■ EJ

+ йф + Ь_ха\

В первом приближении упростим криволинейное очертание эпюр моментов. Для этого заменим криволинейные дуги прямыми линиями. Эпюра моментов при этом будет состоять из 4 треугольников.

Разобьем пролет I на участки: 1-й участок — 0 < х < 6;

2-й участок — 6 < х < 8;

3-й участок — 8 <  х <  12;

4-й участок — 12 < х < 18;

5-й участок — 18 < х < 21;

6-й участок — 21 < х < 24.

Тогда формула трапеции для определения перемещения сечения К сведется к виду

, ^МкМп,   6.МкМп,

5_кп = £/——-^ = Zf—— dx^ q hj        о EJ

+ 2№ 6

^МкМп

, ^²МкМп ах + У ]-------

8 EJ dx + У J------ 18 Ej dx +

dx +

2*MkMn .

J-------- dx.

21 EJ

При подстановке получим: 1-й участок: Z - 6 м.

б¹ =-^_(2-1,0-0,375) = -—;

'hn 6EJ             EJ

2-й участок: / = 2 м.

dkn=d\ + 5? + 5? +5_fc⁵ +dL = кп кп кп кп кп кп

0,75 +1,19 + 0,59 + 2,25 + 4 +1,476 _

EJ

10,265.

EJ

Во втором приближении заменим криволинейные дуги прямыми линиями. Эпюры моментов будут состоять из 4 треугольников (двух у опор и двух у ключевого шарнира С) и 20 трапеций.

Как и в предыдущем случае, разобьем всю длину Z на участки:

1-й участок — 0 <  х < 6;

2-й участок — 6 < х < 8;

3-й участок — 8 <  х < 12;

4-й участок — 12 <  х < 18;

5-й участок — 18 <  х < 21;

6-й участок — 21 < х < 24.

Тогда формула трапеции для определения перемещения сечения К снова сведется к виду

5 ²₌ _ _2_ (2.1,779.0,333 + 2 -1 • 0,375 + 6 ■ EJ

+1 • 0,333 +1,779 • 0,375) = -—;

3-й участок: Z = 4 м.

5? = —— (2 ■ 1,779 - 0,333) = -^;

кп 6EJ              EJ

4-й участок: Z = 6 м.

5»„-

”6 А И 2,25 -------(2 • 1,0 ■ 1,125) ---;

6 EJ             EJ

. _1.МкМп, ^MkMn ,

6 EJ          EJ

^М^^МьМ^

12 EJ        ₁₈ EJ

21 EJ

5-й участок: / = 3 м.

S3 =—— (2,952 + 2,25 + кп 6EJ

+ 0,843 + 1,968) = -——;

EJ

6-й участок: / = 3 м.

»^ =-^-(2 0,75 068) = -^;

^Rn 6 ■ Ej                  EJ

Вычислим 5^_п при 0 <  х < 6, I = 6 м: д^ = -2L [(0,006) + (0,046 + 0,006 + + 0,005 + 0,012) + (0,14 + 0,046 + 0,052 + + 0,031) + (0^95 + 0,14 + 0,083 + 0,124) + + (0,505 + 0,295 + 0,231 + 0,162) + + (0,75 + 0,505 + 0,364 + 0,260) ] - - 5^5.

Вычислим 0^ при 6 <  х <  8 ,1 = 2 м:

⁵кп =        1⁽⁰'^{99 +} °-^{75 +} °-^{51 +} °-³64) ⁺

+ <1,185 + 0,99 + 0,45 + 0,64)] = ^.

EJ

Вычислим <5^_ппри 8 <  х <  12, Z ^ 4 м:

5 ² = —— [ (0,082) + (0,082 + 0,324 + 6EJ

+ 0,089 + 0,075) + (0,324 + 0,702 + 0,26 +

+ 0,218) + (0,702 +1,184 + 0,5 + 0,416)] =

_ 0,826 EJ

Вычислим 6^_п при 12 <х < 18, / = 6 м:

8^ = ^j [ (0,116) + (0,323 + 0,116 + + 0,075 + 0,089) + (0,702 + 0,323 + 0,259 + + 0,218) + (1,182 + 0,702 + 0,415 + 0,5) + + (1,72 +1,182 + 0,647 + 0,785) + ____ ..„ ____ _____ 2,55 + U/3 + 1,/2 + U,#«D + l,Uy?J = ——,

Суммируем вычисленные результаты: гь=3*„₊^,₊3^₊8^₊5^₊^ =

0,676 + 0,98 + 0,826 + 2,55 + 4,13 + 1,57 _ "             EJ

10,732 EJ "

Перемещения сечения К от действия единичной силы, приложенной в точках 2 и 5, были получены по вышеприведенной методике. Они были равными соответственно:

при первом приближении:

10,172       _ 16,833 .

EJ ’ ^кп" EJ ' при втором приближении:

9,68 . .      15,95

EJ ’ кп EJ

Результаты расчетов сведены в табл. 1.

Определим перемещение сечения К арки от действия единичной силы, приложенной в точке 16. При исходных данных I = 24 м, f = 6 м, а = 3 м, b = 21 м, А — 16 м, и = 8 м выражение для определения в данном интервале имеет вид

Вычислим 5^ при 18<х<21, / = 3м:

8? = —— [ (2,952) + (2,958 +1,747 + ^кп 6 • EJ

+1,249) + (2,958 + 2,69 +1,619 +1,229) +

+ (2,25 + 2,69 +1,385 +1,09)] = ~™j

Вычислим 8^_п при 21 < х < 24, / = 3 м:

Окп=^ J -x-_t— dx = J       dx +

0 EJ^ ₀ EJ₀

JiM^dxJsM^Ldx = m EJ0 b EJq

1 _rm³ a(2m-E) x⁴ 1a

EJq 3

4m6

5/4

Z2

1 EJq

4      /3

b³ - m³ 4am

6⁴ - m⁴ - Sam 5 ²

6®_п = ^у №88) + (1,433 + 0,388 + + 0,395 + 0,352) + (2,952 +1,432 +1,092 + + 0,968)] = -^.

4 Z3

4dm) x—- ■

Z4

3 Z2

- m² am b⁵ - m⁵

"2 F+ 5 X a3 m(2a - b)

T-z2  +

d⁴ 2m(6-3d) 4ama^

Z3

5Z4

Вычислим численные значения этой величины:

1 г83 3(2-8-16) 84 16-3-8

’kn'EJV 3    242   + 424

212 -82 3-8 215- 85 4-3-8 —---|----—_—р

2    24      524

З³ 8(6-21) З⁴ 2-8(21-3-3)

+ 3   242   + 4     243+

+ 4'3 ‘ 8 ’ 3 = 1 (-98,304 - 8 738,13 +

5-24424

+ 6 719,232 - 7 352,934 - 2 605,824 +

3241,066 - 25,920 + 3,888 + 194,4) =

-127,319 19,21

24³ £J    EJ

Точно так же вычисляется 5^ сече ния К арки от действия единичной силы, приложенной в точках 2 и 5. Они равны 9,21 _ 15,61 соответственно ТГ7* г"'

EJ EJ

Результаты вычисления перемещения сечения К арки от действия единичной силы Р_п = 1 с помощью программы Lira 9 приведены на рис. 2. Ординаты точек показывают величины перемещений точки К при нахождении единичной силы Р_п = 1 над этими ординатами.

Согласно рис. 2 для точек 2, 5 и 16 они имеют соответственно значения

11,281 16,508 _ 10,907

EJ ’ EJ EJ ‘

Подсчитаем расхождение результатов относительно вычисленных методом непосредственного интегрирования по формуле

А = ^1—— 100 %.

*2

Полученные результаты сведем в табл. 2.

Таблица 2

Номер точки	Расхождение результатов формулы трапеции,%		Расхождение результатов с программой Lira 9, %	Расхождение результатов с методом непосредственного интегрирования, %
	в 1-м приближении	во 2-м приближении
2	10,4	5,1	22	0
5	7,8	1,9	0,7	0
16	11,45	16,5	18,4	0

Как видим, наибольшее расхождение с теоретическим решением наблюдается в случае использования программы Lira 9, что связано с исходными предпосылками построения линии влияния перемещений. В нашем случае, как это следует из [2], не учитывалось влияние продольных и поперечных сил на величину перемещения. В программе Lira 9 данные усилия учитываются.

При построении линии влияния методом Верещагина имеет смысл разбивать эпюры М_п и Мк на большее количество участков, о чем свидетельствует сравнение строк 1 и 2 табл. 1 и табл. 2.

Отметим, что полученные результаты дают несколько заниженные перемещения по сравнению с найденными с помощью программы Lira 9 (до 22,0 % ) и приближенного метода (до 16,5 %).