Проводящие полимерные композиты на основе тканей

Прогресс робототехники обусловливает необходимость разработки и массового применения различных резисторов, антенн, тензодатчиков и датчиков деформаций из эластичных материалов. Кроме реализации больших деформаций в некоторых случаях к тезодатчикам предъявляются требования совместимости с тканями верхней одежды и нижнего белья, высокой тензочувствительности в широком диапазоне удлинений [1, 2].

Тензодатчики и датчики деформации содержат, по меньшей мере, два основных элемента: подложку и электропроводящий слой полимерной композиции [3–5].

В известных на рынке [6, 7] датчиках, датчиках деформации и средствах измерения параметров движущихся объектов наиболее часто в качестве подложек датчиков деформации применяются синтетические полимеры [8], такие как карбоцепные каучуки, полиорганоси-локсаны, имеющие относительное удлинение при разрыве порядка тысячи процентов [9]. Для того чтобы совмещать тензодатчики деформации с одеждой и применяться различные волокнистые тканые и нетканые материалы [4].

Цель работы – получение электропроводящих датчиков деформации на основе эластичных волокнистых материалов.

Материалы и методы

В качестве объектов исследования использовали следующие вещества, полимерные материалы и ткани.

Ткани:

• •    ткань саржевого переплетения марки Лицей Асtivе280, арт. 37017, смесового состава волокон: 48% Вискоза, 48% полиэфир, 4% полиуретан, (производитель ООО «Чайковская текстильная компания»);

• •    трикотажное полотно кулирного переплетения, смесового состава волокон хлопок 65%, полиэфир 35%, применяемое для пошива для нижнего белья и внутренних слоев специальной одежды (производитель (ВФТП «Тривел»).

Модификаторы электропроводности:

• •    одностенные углеродные нанотру-боки марки TUBALL™ СОАТОСSiА, в форме водной суспензии;

• •    электропроводящий пигмент для красок марки Printex XE 2-B; технический углерод марки F-200GS; порошок технического углерода марки AX-020;

• •    дисперсия графита с политетрафторэтиленом в пропаноле-2 спрей в аэрозольной упаковке марки Graphit 33/200.

Растворы полимеров для модификации тканей в аэрозольной упаковке:

• •    раствор сополимера этилена с винилацетата в о-ксилоле в аэрозольной упаковке марки Tesa 60150;

• •    раствор сополимера стирола, бутадиена и изопрена в стироле марки Krylon 7777-Super QuickGripSprayAdhesive.

Диаметр и среднее распределения частиц графита и нанотрубок по размерам (рисунок 1) определяли с помощью лазерного анализатора частиц Микросайзер 201 фирмы «ВА ИНСТАЛТ».

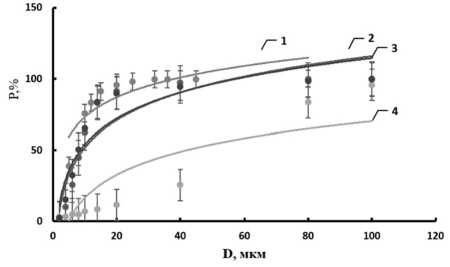
Рисунок 1. Интегральное распределение частиц углерода в дисперсии (Р,%) по размерам: 1 – электропроводящий пигмент для красок; 2 – технический углерод; 3 – дисперсия графита с политетрафторэтиленом в пропаноле-2; 4 – одностенные углеродные нанотрубоки

Figure 1. Integral distribution of carbon particles in dispersion (P,%) by size: 1 – electrically conductive pigment for paints; 2 – carbon black; 3 – dispersion of graphite with polytetrafluoroethylene in propanol-2; 4 – single-walled carbon nanotubes

Образцы для испытаний размером 10 x 80 мм вырезали из полотен промышленного производства, поверхность которых покрыта слоями растворов сополимеров и дисперсией графита с политетрафторэтиленом. Слои растворов сополимеров наносились путем напыления из аэрозольной упаковки с контролем изменения массы после сушки.

Водная суспензия одностенных нанотрубок TUBALL™ СОАТОСSiА с добавкой полиоксиэтиленгликолевого эфира ОС–20 и неионогенного поверхностно-активного вещества ОП–7 после ультразвуковой обработки наносилась на поверхность тканей трафаретным способом печати. Суспензия продавливалась ракелем через печатную форму с сеткой линиатурой 120 lpi. Образцы изготавливались в лабораторных условиях при температуре 24 ± 2С и сушились при относительной влажности 45–50% до постоянной массы.

Электропроводящие пигменты, графит и технический углерод в виде порошка наносились сверх слоев сополимеров методом напыления.

Серии по пять образцов ткани и ткани с покрытием каждого вида для механических испытаний вырезаны в четырех направлениях относительно расположения нитей основы тканей: вдоль, поперек и по диагоналям под 45 и 135 градусов.

Датчик деформации с покрытием дисперсией графита и / или нанотрубок, получали следующим образом: образцы разрезали на ленты длиной 100 мм, размещали зеркально и укладывали отрезки друг на друга, т. е. производили дублирование отрезков пленки со слоем клея и электропроводящего наполнителя, совмещением слоев электропроводящего наполнителя внутри датчика (рисунок 2).

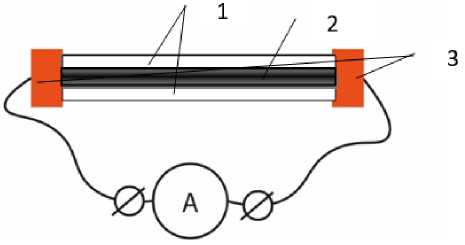
Рисунок 2. Схема сборки тензодатчика для испытаний электропроводности: 1 – слои волокнистого материала; 2 – слой дисперсии электропроводящего наполнителя; 3 – электроды (медная фольга)

Figure 2. Assembly diagram of aload cell for electrical conductivity tests: 1 – layers of fibrous material; 2 – layer of dispersion of an electrically conductive filler; 3 – electrodes (copperfoil)

По концам отрезков между слоями укладывали плоские электроды из медной фольги с проводом. Таким образом производили соединение слоя графита с источником постоянного тока и измерителем электрического сопротивления.

Коэффициент чувствительности тензодатчика к деформации GF вычисляется по формуле:

A R / R 0 A 1 / 1 ₀

где R 0 – начальное сопротивление датчиков, Ом, ∆ R – относительное изменение сопротивления при деформации Ом, l 0 – начальная длина датчика, м, а ∆ l – абсолютное удлинение, м.

Тензочувствительность датчика QF к механическому напряжению при деформации растяжения вычисляется по формуле:

QF =

A R / R 0

Act

где, R 0 – начальное сопротивление датчиков, Ом, ∆ R – изменение сопротивления датчиков при деформации растяжения, ∆ σ – увеличение механического напряжения [Па].

Результаты

В датчиках деформации и резисторах чувствительных к составу среды [8–11] подложка является внешним слоем, определяющим их механические свойства и тензочувстви-тельность. Использование тканей и трикотажа в сочетании с полимерной пропиткой позволяет подготовить подложки с различной податливостью в широком диапазоне обратимой деформации, снижающейся на порядок при достижении определенного предела растяжения что соответствует податливости кожи человека и теплокровных животных [8, 9].

Деформация ткани вдоль и поперек расположения нитей основы определяется механическими свойствами нитей и существенно зависит от типа плетения. Продольная и поперечная деформация нитей в ткани саржевого переплетения невелика и не обеспечивают достаточной для датчиков податливости.

Рассчитанное по геометрической схеме значение деформации «смятия» по диагонали квадратных ячеек переплетения нитей в ткани отличается от значений относительного удлинения вырезанных из ткани образцов с покрытием на лицевой стороне. Это обусловлено тем, что эластичная композиция первого слоя, содержащая полимер, проникает в структуру ткани и обеспечивает дополнительную связь между нитями по внешней поверхности. Полимерное связующее образует пленку и обеспечивает связь между концами обрезанных волокон, что не позволяет им рассыпаться при растяжении. В результате образуется композиционный материал с механическими свойствами, существенно отличающимися от механических свойств ткани. За счет связи между волокнами и разрезанными нитями значения относительного удлинения вырезанных из ткани лент достигают 100%, что в 2,2 раза больше, чем у аналогичного образца ткани без покрытия. Для деформации и разрушения ткани с полимерным покрытием необходимо приложить большее напряжение. Значение прочностиоб-разца с двумя слоями полимерной композиции, нанесенной напылением аэрозоля, превышает предел прочности ткани на порядок.

Нанесение дисперсии графита, технического углерода и нанотрубок делает ткани электропроводящими (Табл. 1) с линейной вольтам-перной характеристикой (рисунок 3).

При близкой дисперсности все исследуемые порошки графита формируют на поверхности тканей покрытых растворами сополимеров слой одинаковой электропроводности (10÷90 кОм). Электропроводящий пигмент для красок марки Printex XE 2–B, по-видимому, содержит дополнительные ингредиенты, наличие которых увеличивает сопротивления слоя на порядок.

Известно использование технического углерода для получения электропроводящих полимерных композитов [11, 15]. Получены смеси полиэтилена с техническим углеродом, стабильность которых оценивается по влиянию температуры и относительной влажности на от-носительноесопротивление. Из результатов видно, что с повышением температуры и относительной влажности значение сопротивления имеет тенденцию к уменьшению, и его зависимость от деформации увеличивается.

Таблица 1.

Электрическоесопротивление трикотажных лент шириной 10 мм

Table 1.

Electrical resistance of knitted tapes with a width of 10 mm

Углеродные наполнители | Carbon fillers	F-200GS	AX-020	Нанотрубки	Graphit 33/200	РrintехХЕ 2-B
Сопротивление, кОм | Impedance, kOhm	10 ± 2	12 ± 3	12 ± 2,5	90 ± 5,8	450 ± 65

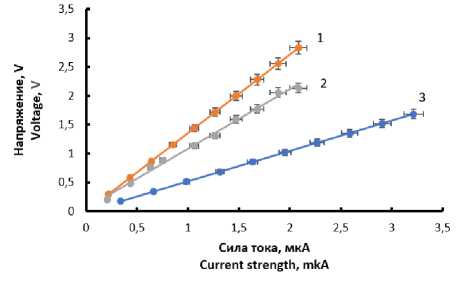
Рисунок 3. Вольтамперная характеристика эластичной ткани саржевого переплетения с электропроводящим покрытием: 1 – технический углерод, 2 – нанотрубки, 3 – графит

• Figure 3.    Voltage characteristic of elastic twill weave fabric with an electrically conductive coating: 1 – carbon black, 2 – nanotubes, 3 – graphite

Добавка политетрафторэтилена, введенная в состав спрея марки Graphit 33/200, для предотвращения агрегации частиц графита имеет незначительный негативный эффект снижения электропроводности. Использование данного модификатора тканей в аэрозольной упаковке представляется наиболее перспективным.

Для обоснования возможности использования тканей пропитанных растворами полимеров и покрытых дисперсиями графита в качестве основы резисторов и прогнозирования их свойств необходимо количественное описание напряжения в ткани, возникающего при растяжении и зависимости электрической проводимости полимерной композиции от деформации.

Для использования тканей с покрытием в качестве тензодатчиков исследовали их деформационно-прочностные свойства.

Диаграмма растяжения датчиков с высокой степенью достоверности (R2 = 0,92–0,99) может быть разделена на два линейных участка (рисунок 4). Первый участок для тканисарже-вого переплетения марки Лицей Active в интервале относительной деформации растяжения 2÷30% в наибольшей степени соответствует практическому применению волокнистого материала для изготовления тензодатчиков и датчиков деформации на спецодежде из тканей и описывается уравнением ϭ = 0,09 ԑ + 0,28. Второй участок в интервале 30 ÷ 100% уравнением ϭ = 0,3 ԑ – 6,74. Для трикотажного полотна кулирного переплетения в интервале относительной деформации растяжения 2 ÷ 30%, который также соответствует практическому применению тензодатчиков зависимость напряжения от деформации описывается уравнением ϭ = 0,11 ԑ + 0,45, а второй участок в интервале 30 ÷ 100% уравнением ϭ = 0,19 ԑ – 4,3.

По технической диаграмме растяжения датчиков видно, что механические свойства на стадии удлинения могут быть охарактеризованы величиной условного модуля упругости: для эластичной ткани саржевого переплетения модуль упругости равен 11 МПа при деформации менее 30% и 30 МПа при больших удлинениях для трикотажного полотна модуль упругости равен 9 МПа при деформации менее 30% и 19 МПа при предельных удлинениях.

Тензочувствительность датчиков к механическому напряжениюна различных волокнистых основах при растяжении представлены в таблице 2.

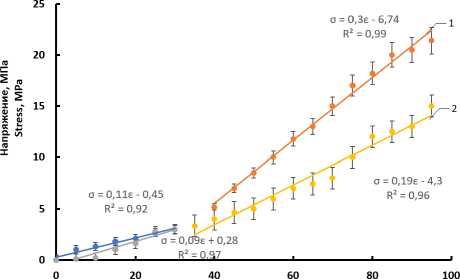
Относительное удлинение, % Relative elongation, %

Рисунок 4. Зависимость напряжения от деформациипри растяжении лент вырезанных по диагонали: 1-эластичная ткань саржевого переплетения, 2 – трикотажное полотно

• Figure 4.    The dependence of stress on strain during diagonal stretching: 1 – elastic twill weave fabric, 2 – knitted fabric

Таблица 2.

Тензочувствительность волокнистых датчиков

Table 2.

Strain sensitivity of fiber sensors

Волокнистая основа датчика	Тензочувствительность Δ F , кПа-1
	Растяжение в диапазоне относительной деформации, %
	0 ^ 15	15÷30
Ткань саржевого переплетения	1234	3765
Трикотажное полотно	1352	4882

Вследствие высокой податливости тканевых подложек коэффициент тензочувствитель-ности во всем диапазоне деформаций превосходит достигнутое значение GF на электропроводящих композитах матричной структуры на три десятичных порядка [16].

Обсуждение

Наличие двух линейных интервалов на зависимости механических и электрических свойств полимерных композитов на основе тканей обусловлено их макроструктурой и наличием синтетического полимера в составе нити. В диапазоне деформаций 0 ÷ 30% расстояние между частицами графита на нитях в направлении растяжения ткани увеличивается вследствие чего частично нарушается их электрический контакт и электросопротивление возрастает. Однако при этом, вследствие боковой контракции ленты и сближения нитей, образуются контакты в поперечном направлении и снижение электропроводности датчика не столь значительно.

При вытяжке более 30% боковая контракция ленты завершается, расстояние между центрами частиц графита на нитях увеличивается, электрические контакты нарушаются с большей интенсивностью и сопротивление возрастает в 40 раз быстрее (рис. 5).

Для определения параметров чувствительности тензодатчика к деформации (GF) достаточно информации об электрическом сопротивлении деформированных образцов многослойных тензорезисторов, выполненных на различных подложках (таблица 3) и значения электросопротивления слоя проводящей композиции до растяжения ( R 0 ).

Коэффициент чувствительности к деформации ( GF ) тензодатчика на основе ткани не превышает 10 в диапазоне деформации в диагональном направлении до 20%, а коэффициент чувствительности к деформации на трикотаже вне зависимости от направления высечки образцов из полотна на два порядка выше и составляет 945 ± 5,2 до относительного удлинения до 30% и 92 ± 2,2 в интервале относительного удлинения 30÷45%.

По данным технологического университета Тоёхас (Япония) наибольшую чувствительность к деформации полимерных композитных тензодатчиков удается получить при использовании наночастиц серебра с размерами менее 100 нм [10]. В пленках из полиди-метилсилоксана с нанодисперсией серебра относительное изменение сопротивления возрастает в 20 раз почти линейно (0,05 ÷ 0,98) при растяжении композитной пленки до 50%. Лабораторный образец такого датчика способен растягиваться до 140%, но сопротивление может быть корректно измерено при относительном удлинении лишь до 60%.

Коэффициент чувствительности к деформации ( GF ) тензодатчика с наночастицами серебра в эластичной матрице, полученного в работе [10] составляет на начальном этапе растяжения 270, а датчика при большей относительной деформации 110. Тензодатчики и датчики деформациис высоким коэффициентом GF полученным за счет монолитной интеграции растяжимой подложки с изменяющейся жесткостью и чувствительной пленки, содержащей перколяционную сеть из нанопроволок серебра признаны соответствующими эксплуатационным требованиям гибкой электроники [17–18]. При этом параметров тензочув-ствительности, т. е. изменению электрического сигнала при изменении механического напряжения в указанных статьях не приводится.

При циклических деформациях растяжения и сокращения датчиков проявляется эффект Патрикеева-Малинза, который заключается в обратимости деформации и существенном различии первого и последующих циклов. Такое явление наблюдается не только в резистивных тензодатчиках, но и в механике композитов органической и неорганической природы [19]. В настоящее время физическая природа эффекта Патрике-ева–Маллинза является объектом теоретических и экспериментальных исследований в коллективах ученых разных стран [20].

(Rl-Ro)\Ro

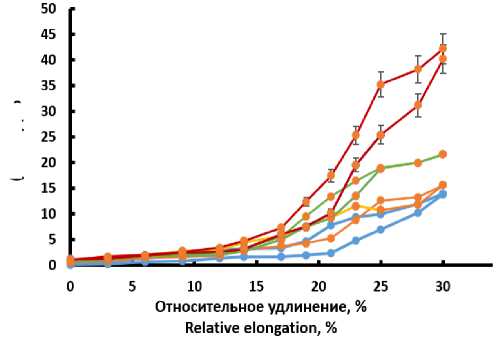
Рисунок 5. Циклическая деформация датчика на основе трикотажа

• Figure 5.    Cyclic deformation of the sensor based on knitwear

На рисунке 5 показано относительное из-менениеэлектросопротивления тензодатчика на основе трикотажа при многократном растяжении. Видно, что первый цикл деформации имеет большее изменение электросопротивления, чем последующие циклы. Это различие имеет место как при растяжении, так и при сокращении. После второго цикла эффект Патри-кеева-Малинза не проявляется. При многократных деформациях гистерезис не превышает 4%.

Гистерезис играет важную роль для тензодатчиков находящихся под динамической нагрузкой. Это эксплуатационный критерий для датчика, который предназначен для использования в качестве носимой электроники. Гистерезис сигнала датчика свыше 8–10% может приводить к потере чувствительности датчика к нагрузке вследствие увеличения доли необратимой деформации [21, 22].

Заключение

Показана возможность получения электропроводящих волокнистых материалов путем послойного нанесения на ткани аэрозолей растворов высокомолекулярных соединений и дисперсий графита в органических жидкостях и / или водной дисперсии углеродных нанотрубок.

Предложено устройство, изготовлены лабораторные образцы и получены вольтампмер-ные характеристики резисторов и тензодатчиков на основе тканей и трикотажа с углеродным покрытием. Установлены линейные зависимости сигнала датчика от деформации, с различными значениями чувствительности к деформации при малых и предельных удлинениях. Коэффициент чувствительности к деформации ( GF ) тензодатчика на основе ткани не превышает 10 в диапазоне деформации в диагональном направлении до 20%, а коэффициент чувствительности к деформации тензодатчика на основе трикотажа вне зависимости от направления высечки образцов из полотна на два порядка выше и составляет 950 до относительного удлинения до 30% и 90 в интервале относительного удлинения 30÷45%.

Определены значения истиной тензочув-ствительности датчиков, полученных напылением суспензии графита на трикотаж, которые вследствие высокой податливости трикотажа достигают рекордных 4900 и 1350 кПа-1 при больших и малых удлинениях соответственно.