Пружинные аккумуляторы с выходным поворотным звеном

• 1.    Закон изменения потенциальной энергии в зависимости от угла поворота.

• 2.    Зависимость усилия пружины от угла поворота выходного звена.

• 3.    Жёсткость и максимальное усилие пружины.

• 4.    Приведённый к оси выходного звена момент трения в шарнирах.

• 5.    Закон изменения движущего момента, который при постоянном приведённом моменте инерции, аналогичен по виду закону ускорения.

• 6.    Зависимость скорости выходного звена от угла поворота.

• 7.    Время поворота на заданный угол, при заданных моменте инерции и жёсткости пружины.

Знание этих характеристик позволяет конструктору осознано выбирать те или иные пружинные аккумуляторы с учётом их основных характеристик и сравнительного анализа при конструировании пружинных приводов и уравновешивающих устройств.

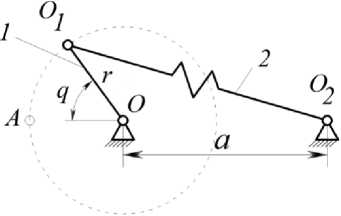
Рис. 1. Схема нелинейного пружинного аккумулятора с выходным поворотным звеном и пружиной растяжения

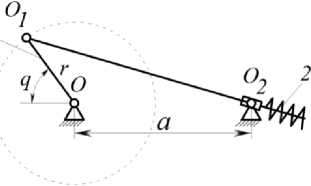
Рис. 2. Схема нелинейного пружинного аккумулятора с выходным поворотным звеном и с пружиной сжатия

Рассмотрим более подробно некоторые из этих характеристик. Момент, действующий на выходное звено, определяется выражением:

М = cL пр h                        (1)

где h - плечо вращающего момента определяется по рис. 3 из соотношения:

ar sin q = h ^r² + а² + 2ar cos q (2)

Для пружинных аккумуляторов, представленных на рис. 1 и 2, выходная моментная характеристика определяется следующим выражением:

М = acr sin q ( 1 - , ^{a r} =) (3)

\    ^r²+a²+2ar cos qj

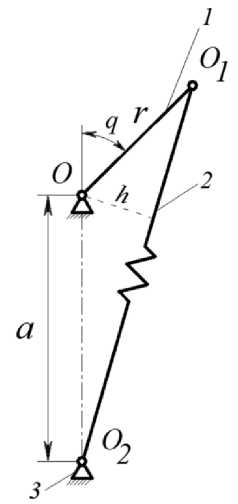
Рис. 3. Схема пружинного аккумулятора для определения геометрических характеристик

Для определения областей изменения межосе- вого расстояния, введем безразмерный коэффициент

a ' = - .

r

М = cr² sin q • М'

) - уравнение, опреде-

где М' = a' I 1 - “r

I-

a ' -1

1+a '2 +2a ' cos q

ляющее значение момента в безразмерном виде.

На рис. 4 в общем виде показано семейство мо- ментных характеристик нелинейного пружинного ак- кумулятора при единичном значении радиуса поворотного звена при различных значениях межосевого расстояния, определяющих моменты на выходном звене. Необходимо отметить, что при увеличении межосевого расстояния амплитудное значение увеличивается и смещается к положению неустойчивого равновесия, при этом площадь, ограниченная каждой кривой, во всех случаях одинаковая – это и есть работа, которая равна максимальной потенциальной энергии.

Для сравнения различных видов пружинных аккумуляторов возьмём пружинный аккумулятор с синусной моментной характеристикой, представленный на рис. 5. Момент такого нелинейного пружинного аккумулятора определяется следующим выражением:

М = M_max sin q (5)

Пружинный аккумулятор с такой характеристикой невозможно реализовать с углом поворота равным 2я по динамическим и конструктивным ограничениям. Однако грузовой аккумулятор позволяет реализовать привод с углом поворота равным 2л [6]. Пружинные аккумуляторы с синусной моментной характеристикой могут быть реализованы в системах уравновешивания звеньев при их вертикальном расположении или при угле поворота q <2и [4].

Определим законы изменения потенциальной энергии для пружинных аккумуляторов, представленных на рис. 1 и 2.

Для рассматриваемых пружинных аккумуляторов с одним поворотным рычагом (рис. 1, 2) при одинаковой жёсткости пружин c и радиусе поворота г, максимальная потенциальная энергия в положении неустойчивого равновесия равна:

V max = 2cr² (6)

где с – жесткость пружины; r=OO 1 – радиус закрепления пружины на выходном звене; q – текущий угол поворота выходного звена.

Текущее значение потенциальной энергии определяется следующим выражением:

V = 0,5cL пр 2

Lпр = ^r2 + a2 - 2ar sin q - L0

где a=OO2 – расстояние между осями выходного звена и шарнирного соединения пружины с корпусом; L0 -минимальная длина пружины, a = r + L0

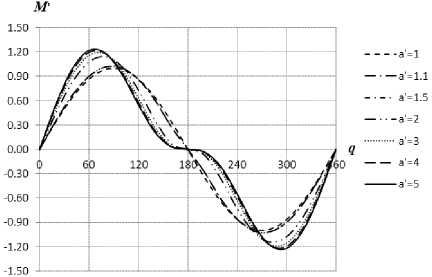
Рис. 4. Семейство моментных характеристик нелинейного пружинного аккумулятора с выходным поворотным звеном

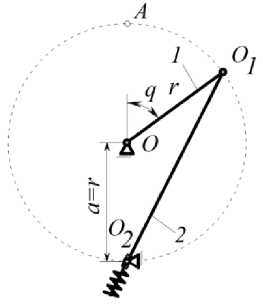
Рис. 5. Схема нелинейного пружинного аккумулятора с выходным поворотным звеном при a = r

Так как максимальное удлинение пружины в рассматриваемом пружинном аккумуляторе равно 2r, то Lo = 2^, Ку - коэффициент удлинения пружины. КоКу- у эффициент удлинения пружины в стандартных цилиндрических пружинах лежит в пределах от 0,5 до 4 [3]. Тогда значения а будут изменяться от 1,5r до 5r, а безразмерный параметр в пружинных аккумуляторах с пружинами растяжения a' е [1,5 .„ 5]. Для пружин сжатия a' е [1,1... 5].

С учётом уравнений (8), (9) уравнение (7), определяющее текущее значение потенциальной энергии, для пружинного аккумулятора примет вид:

V _m = j (7^r 2 + a² + 2ar cos 4 - L_o)           (10)

V m =^ v                          (ii)

где V = (V1 + a ' ² + 2a ' cos q - (a ' - 1)) - уравнение, определяющее значение потенциальной энергии в безразмерном виде.

Текущее значение потенциальной энергии в зависимости от угла поворота для всех представленных выше схем будут определяться их конструктивными параметрами. Семейство графиков зависимости потенциальной энергии от угла поворота в общем виде представлено на рис. 6. Зависимость потенциальной энергии для синусного пружинного аккумулятора от угла поворота q определяется выражением:

V = 2cr2 • cos2 ^

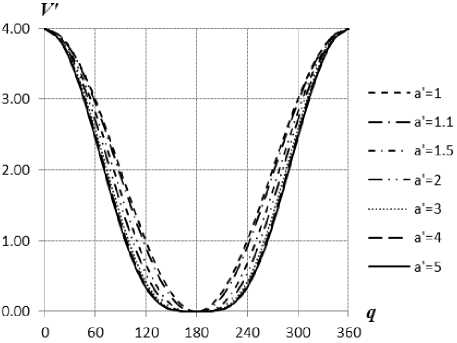
Рис. 6. Зависимость потенциальной энергии нелинейного пружинного аккумулятора от угла поворота: V = f(q)

Текущее значение усилия пружины, с учётом уравнений (8), (9) определяется следующим выражением:

Рпр = cL пр(13)

или

Р _пр = c(7^r 2 + a² + 2arcosq - L_o) (14)

Рпр = сгВПр (15)

где Р пр = 71 + a ' ² + 2a' cos q - a' + 1 - уравнение, определяющее значение усилия пружины в безразмерном виде.

Графики зависимости усилия пружины нелинейного пружинного аккумулятора от угла поворота представлены в общем виде на рис. 7.

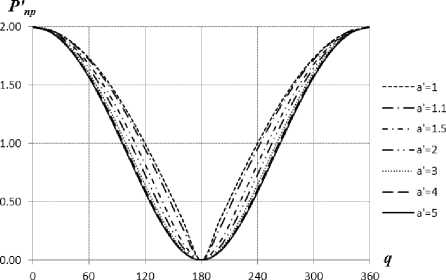
Рис. 7. Зависимость усилия пружины нелинейного пружинного аккумулятора от угла поворота: Р _пр = f(q)

Для определения скорости выходного звена за- пишем уравнение полной механической энергии НПА, без учёта диссипативных потерь:

V_ma x - V m = ^                (16)

Текущая угловая скорость определяется из уравнения (15) для полной механической энергии не- линейного пружинного аккумулятора и равна:

q=J

2(У т_Дх -У т )

Максимальная угловая скорость выходного зве- на имеет место при прохождении положения устойчи- вого равновесия и равна:

jfjcr^{2 q} =.

-0,5c^7 ^r 2 + ct² + 2ar cos Q-L q ) )

^q =

•q'

1+a^,2 + 2a ' cos q-(a ' -1)^

где q ' = ^J1 -^

уравнение, определяющее значение угловой скорости в безраз- мерном виде.

На рис. 8 в общем виде показано семейство графиков зависимости угловой скорости нелинейного пружинного аккумулятора от угла поворота. Зависимость угловой скорости выходного звена от угла пово- рота для синусного аккумулятора имеет вид:

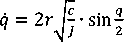
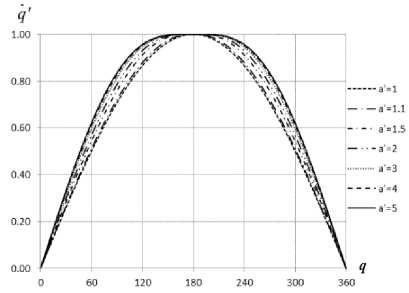
Рис. 8. Зависимость угловой скорости нелинейного пружинного аккумулятора от угла поворота: q = f(q)

Рассмотрим, какие законы движения можно получить с помощью нелинейных пружинных аккумуляторов с выходным поворотным звеном. При угле поворота, равным 2я , можно получить или точный синусоидальный закон ускорения (грузовой аккумулятор), или синусоидальный закон, в котором скорость и ускорение меняются непрерывно, и свои изменения начинают и оканчивают нулевыми значениями. Время поворота для нелинейного пружинного аккумулятора на угол 2т г определяется интегральным уравнением:

^ =                                  (21)

Это уравнение можно записать в виде

' =    \  ^'^к«         (2²)

При решении данного интегрального уравнения для синусного аккумулятора в первом приближении получаем значение коэффициента Ktq = 24,5, для пружинного аккумулятора при a' = 5, получаем значение коэффициента Ktq = 19,6. Следует отметить, что увеличение а' приводит к увеличению быстродействия и уменьшению времени поворота. Решение уравнения (22) позволяет определить время поворота и, следовательно, жесткость пружины. Изменения конструктивного параметра – длины рычага r позволяет уменьшать или увеличивать жесткость пружины.

При создании пружинных приводов основными параметрами являются момент инерции и требуемое время поворота. Знание основных характеристик позволяет конструктору осознано выбирать те или иные пружинные аккумуляторы с учётом их основных характеристик и сравнительного анализа при конструировании шаговых приводов. В отношении плавности поворота пружинный привод на базе нелинейного пружинного аккумулятора с выходным поворотным звеном и углом поворота 2 я является идеальным, так как скорость, так и ускорение меняются непрерывно, и своё изменение начинают и оканчивают нулевыми значениями. Применение пружинных аккумуляторов оправдано их малыми габаритами и высоким быстродействием.

Рассмотренные выше нелинейные пружинные аккумуляторы имеют рабочий угол поворота равный q = 2я. Такие пружинные аккумуляторы могут использоваться, как в приводах с компенсацией диссипативных потерь в процессе движения, так и в приводах с их предварительной компенсацией. В последнем случае в положении устойчивого положения пружина должна иметь предварительный натяг.