Pseudo Random Ternary Sequence and Its Autocorrelation Property Over Finite Field

Published Online September 2017 in MECS DOI: 10.5815/ijcnis.2017.09.07

- 1

if x = 0

else if x = nj .

otherwise

T = { t .} for i = 0,1,2, _ , n - 1, _ ,          (18)

where t e { 0,1, -1 } and n is the period of the proposed ternary sequence such as n = p^m -1.

F. Autocorrelation

The autocorrelation R_T ( x ) of the ternary sequence

T is generally defined as follows:

The proof for each case of (23) is explained below. It should be noted that, here n = ( p^m - 1 )/( p - 1 ) , j = 0,1,2,3, ^ , and i is mainly appeared at summations and holds the relation 0 <  i <  n = ( p^m - 1 ) .

B.1. The case of ^x = ⁰

In this case, the autocorrelation of the ternary sequence T is calculated as follows:

n - 1

i = 0

n - 1

Rt (x) = E i=0

/Р

Tr ( to i ) + A/ ) /p

where, x represents the shift value.

• III.    Proposed Ternary Sequence

This paper proposes a ternary sequence T . This section introduces its definition and then mathematically shows the autocorrelation property of this proposed sequence.

The case that Tr ( to i ) = 0 appears p^m -1 times. When the shift value is equal to 0, Tr ( to i ^{+ x} ) and Tr ( to ) are the same. The Legendre symbol returns only { 0,1, and -1 } values. Based on this condition, all the possible values become ( 0 x 0 ) = 0, ( 1x1 ) = 1, and

( -1х-1 ) = 1  . Depending on whether or not

Tr ( ю ' ) + A = 0, (24) becomes as follows:

Rt(x)=  2  0 +  2

Тг ( ю ) + A =0     Tr ( ю ' ) + A #0

= pm1 • 0 + (pm-1 - pm-1)-1,(25)

where, ' = 0 ~ p m - 2. Thus, the following relation is obtained for the case of x = 0,

RT (x) = pm -1- pm-1.(26)

• B.2.    The case of x = nj

*                       p m - 1 ) / ( p - 1 )

Let g be a generator of F m . Then gis a non-zero element in the prime field F and is also a generator of F *. Therefore, from here on g(p )(p ) will be denoted as gˆ. Based on the linearity of the trace function, the autocorrelation is calculated as follows:

' g ir ( ю ) + a

n - 1

R t ( X ) = 2

' = 0

k

• •    X # ( - ( g j ) х A ( 1 - g j ) ,       because       of

g- j Tr ( ю ' ) + A # 0, thus Y cannot be 0.

• •    A ( 1 - g^j ) X 7¹ does not become 0, thus Y # g^j .

• •    X = A , where Tr ( Ю ) = 0 appears   ( p m ^-1 - 1 )

times. Therefore, the case that Y = 1 appears ( p^{m -1} - 1 ) times.

• •    The other cases, where Y is the element of F - { 0,1, g^j } appears p m ^-1 times.

From the above conditions, following formula is obtained:

^{p -1}                   j

R_T( x ) = У| /1- p m ^-1 1 ^ g / I-  / .     (31)

^T     p    pp

Y =0 V/            k ' ' 7 V

According to the property of the Legendre symbol, following relation is obtained for the case of x = nij ,

R ( x ) = - pm ^{- 1}1 ^g/ I- 1

^t '   '     * i / p j

= ( - 1) j ^{+ 1} p m ^{- 1} - 1.

According to the Property 1 and (13), the above equation can be rewritten as-

• B.3.    The default case (otherw se)

In this case, the autocorrelation is calculated by-

Rt (X )=  2  0 +2 0 + gjTr(ю)+ A=0    Tr(ю)+A=0

g ^JTr ( ю ' ) + A#0

'§JTr (ю')+A/' /p k                 7

' Tr ( ю ' ) + A/

/p k              7

Tr ( ю ' ) + A #0

Depending on the Property 3 and Property 4,

R t ( X ) =    2

g j Tr ( Ю ) + A # 0

Tr ( Ю ) + A # 0

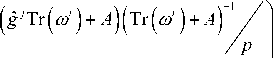
Let, X = Tr ( Ю ) + A , then X # 0, the above equation is rewritten as,

R_T ( x ) =

g j Tr ( ю ) + a #0

f^{( g}

+ A ( 1 - g

) XVA / p

Тг ( ю ' ) + A #0

n - 1

R t ( x ) = 2

I = 0

r ^{Tr (ю + x} ) + A/

/ p k

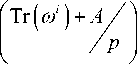
Here x is not divisible by ni and o ^x does not belong to F _p .

By using Ю , consider the following basis W in

W = {®x,1, a2, a3,^, am-1}.(34)

Again let B be the dual basis of W .

B = {Д„ в1, £2,..., Pm-1}.(35)

Assume that Ю can be represented like this- m-1

l = 0

Now, let ( g j + A ( 1 - g j ) X, ¹ be denoted by Y . Then following conditions and facts should be noted:

Then, Ю+x is expressed by- m-1 i+x             xx to — 2 ci, 1P1® .

l — 0

Based on the Property 6, the initial value of Tr( to ) is given by, Tr( to ) — c ,. Hence W and B are the dual basis to each other, then the value of Tr( ® ' ^{+ x} ) is given by Tr( to ^{i + x} ) — c ₀. Substituting the values of Tr( to ) and Tr( ® ' ^{+ x} ) in (33), the following equation is obtained:

Let f ( x ) be x ⁴ + x ³ + x ² + 2 x + 2, which a primitive polynomial over F . Here, the period of the sequence T becomes p^m -1 — 80 and the sequence becomes as follows:

T — {01111111010110011111

11100111110011111010 10000100101101110101 10111110001101110111}.     (42)

i — 0

The autocorrelation of T is given as follows:

By considering all the cases inside the Legendre symbol, the above equation can be rewritten as-

	"53	if x — 0
R T , ( X ) — '	26	else if x — 40	(43)
	- 1	otherwise,

RT(x)— Z ci,0 + A #0

c ,1 + A *0

+ Z ⁰ + Z ⁰ + Z 0.        (39)

c ,o + A — 0       с,- о + A * 0       с,- о + A — 0

c i ,1 ⁺ A * 0       c i ,1 ⁺ A ^{— 0}       c i ,1 ⁺ A ^{— 0}

Since to cannot represent the zero vector, the number of vectors such that c_{z 0} — 0 and c_iX — 0 is one less than that of the other combinations like c_z0 — 0 and c_n — 1. Thus, the last subtraction is required in (40).

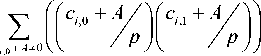
c , ,1 + A # 0

p-1 р-V/     ,\ / i pm-2 SZ ((ab/pMУ■)}

According to the Property 2, the first part of above (40) will become 0 . Thus, the following relation is obtained,

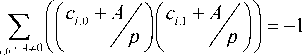
d ⁺ A # 0

and Fig. 1 shows its autocorrelation graph.

• B.    Analysis for p — 7, m — 3 and A — 6

Let f ( x ) be x ³ + 6 x ² + 6 x + 2, which a primitive polynomial over F . Here, the period of the sequence T becomes p^m -1 — 342 and the sequence becomes as flows:

T6 — {10111100111101111111111011111101

1111100100111010111110101011111111 1110111111111111011111011011111111 1111111110111111111111001111111111 1111111111111111111011111111111111 1111111111111111101101101111111111 1111101110011111111110111111111101 1111111101111111010111011111101111 011010111111110111111110111111111111}. (44)

The autocorrelation of T is given as follows:

Finally, the autocorrelation of the ternary sequence T in (23) is proven.

	■ 293	if x — 0
R T 6 ( x ) — -	48	else if x — 57,171,285
	- 50	else if x — 144,228
	- 1	otherwise,

• IV. Result and Discussion

This section experimentally shows the autocorrelation property of the proposed ternary sequence with some examples. The notation T , denotes the proposed sequence with the parameter A — 2. Throughout this section, { -1 } is represented by { 1 } .

• A.    Analysisfor p — 3, m — 4 and A — 2

and Fig. 2 shows its autocorrelation graph.

C. Analysis for p — 11, m — 2 and A — 5

Let f ( x ) be x ² + 5 x + 2, which a primitive polynomial over F . Here, the period of the sequence T₅ becomes p^m -1 —120 and the sequence becomes as follows:

T = {101111110110111111111111111111

1 1111011110111 1 1 1 11111 11111001

111111011111111111111111101011}. (46)

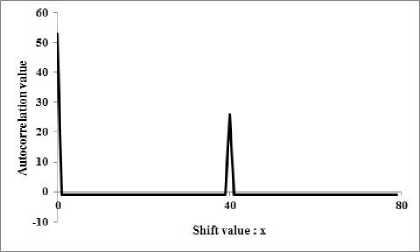
Fig.1. R_T ( x ) with p = 3, m = 4 and A = 2.

• D. Analysis for p = 13, m = 2 and A = 10

Let f ( x ) be x ² + 4 x + 11, which a primitive polynomial over F . Here, the period of the sequence T₁₀ becomes p m -1 = 168 and the sequence becomes as follows:

T10 = {1110111111010111111111111111

1 111 1 1 11 11101 1 11 11 1011011111 1111111111111111111111111111 1111111111111111111111101111 1011111111111001110111111111

11 11110111111111011111 1 11 1 11}.  (48)

The autocorrelation of T is given as follows:

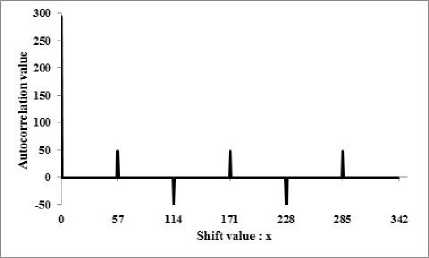
Fig.2. R_T ( x ) with p = 7, m = 3 and A = 6.

	' 155	if x = 0
R ( x ) = -	12	else if x = 14,42,70,98,126,154  ^
	- 14	else if x = 28,56,84,112,140
	- 1	otherwise,

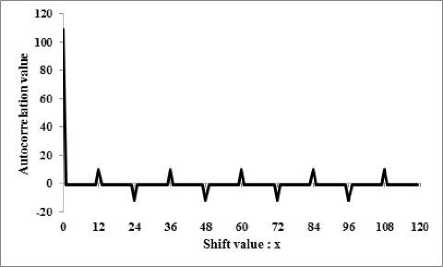
Fig.3. R_T ( x ) with p = 11, m = 2 and A = 5.

In this sequence 0,1,and - 1 appears 11, 54, and 55 times, respectively. This also ensures the identical appearance of 1 and - 1 in the whole sequence. The autocorrelation of T is given as follows:

and Fig. 4 shows its autocorrelation graph.

• E.    Analysis for p = 17, m = 2 and A = 8

Let  f (x)  be  x2 +15 x +12,  which a primitive polynomial or F . Here, the period of the sequence T becomes pm -1 = 288 and the sequence becomes as follows:

T = {11111111111011101111111111111111

11111111111111111111111111111111 11 1011110011111111111111101 11111 1111111111111111 1111110111111111 11110111111111111111111111111111 11111111111111111111111111101111 11111111110111111111111111111111 11110111111101111111111111111110

11111111110101111110110111111111}. (50)

The autocorrelation of T is given as follows:

271    if x = 0

[ 109

^R t , ⁽ x ) = '

- 18

else if x = 18,54,90,126,162,198,234,270

^R T 5 ^{( X} ) =

- 12

—

if x = 0

else if x = 12,36,60,84,108 else if x = 24,48,72,96

otherwise,

- 1

else if x = 36,72,108,144,180,216,252 otherwise,

and Fig. 3 shows its autocorrelation graph.

and Fig. 5 shows its autocorrelation graph.

• F.    Features of the sequence

By observing all the above autocorrelation graphs, it is found that the period n of the sequence becomes

maximum by setting the parameters p , m , and non-zero A . The autocorrelation of the proposed sequence has been mathematically shown in (23). This equation also theoretically guarantees the maximum period.

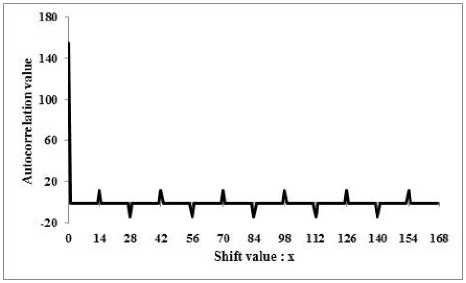
Fig.4. R_T|o ( x ) with p = 13, m = 2 and A = 10.

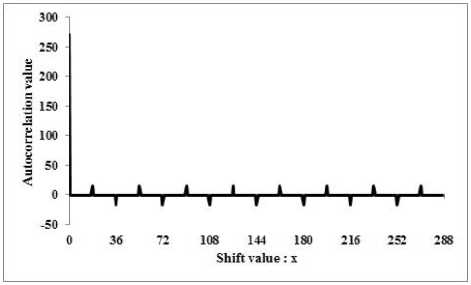
Fig.5. R_{T g}( x ) with p = 17, m = 2 and A = 8.

One crucial point about the non-zero prime field scalar value A is that, by adding this new parameter A does not have any impact in the autocorrelation calculation because (23) confirms that autocorrelation does not depend on the value of A . However, each individual value of A is responsible for generating completely different sequences.

In addition, for each case, the autocorrelation has ( p - 1 ) peaks only such as in Fig. 1 - Fig. 5. Among all the peaks, only one of them has the maximum value. As example, in Fig. 2 the maximum peak value is 293 that corresponds to the case of x = 0 in (23). The other ( p - 2 ) smaller peaks conforms the case of x = nj in (23). Except the ( p - 1 ) peaks, other parts in the autocorrelation graph always have a constant value of - 1, which corresponds to the last case in (23). Therefore, the autocorrelation graph can be explained by (23).

The autocorrelation and cross-correlation properties of a sequence are important in the code division multiple access (CDMA) communication systems, where the ternary sequence of having low values of the autocorrelation property can be used as a signature sequence for each user. Additionally, this can improve the self-synchronization capability of the CDMA communication system [14]–[16].

• V. Conclusion and Future Works

In this paper, the authors have proposed an approach to generate a ternary sequence by utilizing a primitive polynomial, trace function, Legendre symbol, and a nonzero scalar A over the odd characteristic prime field F m . Choosing the parameters p,m, and A, the number of peaks and the length of the sequences are appropriately controlled. In addition, the mathematical proof of typical features like the period and autocorrelation are also explained in this paper. Furthermore, these properties of the proposed sequence are also observed based on some experimental results.

As future works, the authors will evaluate the linear complexity of their proposed pseudo random ternary sequence. In addition, more efficient calculation procedure will be introduced. Furthermore, the evaluation of the cross-correlation property of the proposed sequence will be one of their important future works.