Псевдоматричный фильтр Блума для задач быстрого сравнения текстов

Задача быстрого нахождения подобных текстов не нова. Исследования идут в течение многих лет и начались с приложений простого текстового поиска в 1970-х гг. [1]. Дополнительный импульс в исследования внесли проекты по расшифровке генома человека и работы в различных областях интернет-индустрии, таких как обнаружение дубликатов веб-страниц [2], фильтрация для вебадресов [3], обнаружение плагиата [4] и мн. др.

Приложения по обнаружению подобных текстов, как правило, используют проверку в два этапа. На первом этапе происходит быстрое формирование предопределенного множества, а на втором осуществляется детальная верификация объектов данного множества. Таким образом, сначала необходимо сократить количество сравниваемых документов с нескольких сот тысяч до сотен или десятков, а затем проводить детальное сравнение, с целью разметки схожих сегментов текста.

Существуют различные подходы к решению задач быстрого сравнения текстов, но для обработки больших массивов текста подходят не все. Один из возможных подходов основан на фильтре Блума, который помогает проводить быстрое определение членства элемента во множестве с некоторой вероятностью ложноположительного результата. Фильтр Блума – это вероятностная структура данных, придуманная Б. Блумом в 1970 г. [5], позволяющая компактно хранить множество элементов и проверять принадлежность заданного элемента множеству.

На этапе предварительного отбора, с целью выявления некоторого количества потенциальных кандидатов, фильтр Блума может успешно проводить быстрый поиск схожих частей текста, осуществляя его при этом в большом объеме документов. Детальное сравнение может быть сделано с помощью других методов, с меньшей производительностью, но с более точным результатом.

Необходимо отметить, что само понятие сходство может быть формализовано различными способами [6]. В данной статье под сходством мы будем понимать идентичные сегменты текста без каких-либо его модификаций. В работе рассмотрены проблемы, связанные с практическим применением фильтра Блума, предложен подход, позволяющий увеличить плотность данного фильтра за счет построения специального индекса, отслеживающего загрузку документа в фильтр. Также рассмотрен алгоритм удаления элемента, сохраняющий локализацию элементов.

Фильтр Блума (далее – ФБ) представляет собой вероятностную структуру данных, позволяющую компактно хранить множество элементов и проверять принадлежность заданного элемента множеству [7]. Основная идея заключается в использовании независимых хеш-функций для представления объекта из множества S = { x ₀, x ₁, …, x _{( n – 1)}} в виде бинарного вектора фиксированного размера m . Фильтр Блума использует k независимых хеш-функций h ₀, h ₁, …, h_{k – 1}, чтобы случайным образом разместить каждый элемент в диапазоне {0, …, m – 1}. Чтобы вставить элемент x в фильтр, значения соответствующих битов для хеш-функций { h_i ( x ), 0 ≤ i ≤ k – 1} должны быть установлены в 1. Чтобы проверить принадлежность элемента x фильтру, соответствующие значения { h_i ( x’ ), 0 ≤ i ≤ k – 1} должны быть вычислены и сравнены со значениями в фильтре. Если все соответствующие биты принимают значение 1, то элемент x принадлежит множеству.

Вероятностное вычисление h_i может сформировать ложноположительный результат [8], который определяется следующим образом [9]:

. (1)

\ т)

Как видно из формулы (1), вероятность ложноположительного результата может быть снижена

* Выполнение данного исследования поддержано грантом РФФИ по теме «Разработка новых структур данных и алгоритмов для задач быстрого сравнения текстов», проект №13-07-98004.

за счет увеличения размера фильтра m . Оптимальный размер фильтра Блума может быть определен исходя из n – количества элементов во множестве S и p´ – степени приемлемого риска получения ложноположительного результата.

Классический ФБ имеет следующие специфические особенности:

• 1.    Вследствие фиксированного размера фильтра m он имеет постоянное время проверки и вставки элементов. Эта особенность делает его привлекательным инструментом для проверки принадлежности элемента большим массивам, так как время проверки не увеличивается при увеличении множества { S }.

• 2.    Удаление любого элемента из фильтра требует его пересоздания. Если один элемент множества { S } должен быть удален, то необходимо пересоздать весь фильтр, так как значение отдельного бита зависит от многих элементов фильтра.

• 3.    Если количество элементов во множестве { S } превысит значение n , то новое значение бинарного вектора фиксированного размера m должно быть пересчитано и фильтр должен быть пересоздан.

С того момента, как ФБ был впервые предложен более 40 лет назад, выполнено множество работ по его модификации, связанных с решением проблем фиксированного размера вектора, локализации и удаления элементов множества. Один из способов решения этих проблем – это использование счетчиков для ФБ [10]. Данный подход позволяет хранить количество инициализаций конкретного индекса. Добавление или удаление элемента фильтра может быть осуществлено с помощью увеличения или уменьшения соответствующего счетчика. Хотя такой подход сохраняет простоту и эффективность проверки принадлежности элемента множеству, но он увеличивает затраты памяти. Например, применение однобайтового счетчика, который может хранить до 255 инициализаций конкретного индекса, приводит к увеличению потребления памяти в 8 раз.

Динамические или матричные фильтры Блума [11] решают проблему фиксированного размера вектора путем добавления дополнительных нулевых векторов размера m . Каждый новый вектор считается новой инициализацией пустого фильтра. Такой подход позволяет осуществлять неопределенный рост элементов S за счет дополнительных проверок, так как членство должно быть проверено в каждой строке матрицы. Количество требуемых проверок линейно зависит от размера фильтра S . Удаление любого элемента в фильтре вызывает только удаление соответствующих строк из матрицы.

Последовательность определенного количества слов или символов принято называть шингл (shingle) или грамматика (grammar) [12, 13]. В данной работе будет использован первый из этих терминов. Как правило, при сравнении текстов шингл – это некоторая символьная последовательность, равная нескольким словам и очищенная от знаков препинания и прочих символов. Полное множество таких последовательностей в документе определяется как текст T = { t ₀, t ₁, …, t_{z – 1}}. Если мы сравниваем два документа T_i и T_j длиной z_i и z_j соответственно и сравнение производим с помощью ФБ, то его размер m должен удовлетворять следующему условию: m ≥ max { z_i , z_j }. И если использовать ФБ для сравнения одного документа T’ с массивом документов { T }, то размер ФБ должен быть достаточно большим, чтобы помещать все документы. Кроме того, если два документа содержат абсолютно одинаковые шинглы и оба помещены в ФБ, то в нем они отразятся одинаковыми значениями функции, равными единицам, и, следовательно, не будет возможности определить источник документов.

Очевидно, что существует аналогичная проблема, когда необходимо удалить документ из сравниваемого множества { T }. S. Geravand и Ahmadi предложили решение по использованию матричного фильтра Блума (далее – МФБ). Их идея заключается в том, чтобы использовать набор фильтров, каждый из которых состоит из шинглов одного документа [14]. Текст, который планируется проверить, помещается в фильтр отдельной строкой и сравнивается с каждой строкой МФБ. Хотя множество независимых фильтров не похоже на классический ФБ, такое множество обладает одним важным свойством: количество XOR-операций проверок членства элемента во множестве для МФБ линейно зависит от размера матрицы. При использовании одинакового фиксированного размера всех строк матрицы сохраняется свойство высокой производительности фильтра.

Этот подход обладает недостатком в виде неэффективного потребления памяти каждой строкой в матрице из-за двух факторов: в одной строке сохраняется только один документ и документы должны быть одной длины m . Последнее дает возможность производить вычисления для фильтра только один раз, что значительно повышает скорость сравнения документов. Первое ограничение может быть ослаблено путем добавления в матрицу дополнительного индекса. Далее рассмотрим такой индекс и алгоритмы его использования.

Псевдоматричный фильтр Блума (далее – ПМФБ) будет состоять из неограниченного коли- чества фильтров Блума одинакового размера [15]. Главное отличие заключается в использовании одного фильтра Блума для хранения не одного документа, а нескольких, если это возможно. Из равенства (1) мы можем найти вектор фиксированного размера m, который позволит ограничить степень приемлемого риска p для элементов максимального количества n [16]:

„2-11-1*2

: : ■ : >;/ .

Зная, что значение m зафиксировано для всего ПМФБ с целью достижения высокой скорости сравнения, мы можем утверждать, что если существует ограничение для размещения одного и только одного документа в одном ФБ, то мы можем встретить его в следующих случаях:

• -    количество шинглов в документе превышает количество элементов массива n - такой документ не может весь быть помещен в одну строку;

• -    количество шинглов в документе намного меньше количества элементов массива n - фильтр заполнен слабо, что приводит к неэффективному использованию памяти.

Субоптимальное распределение памяти будет требовать, чтобы степень приемлемого риска p была немного меньше, чем максимальное количество n . Чтобы обеспечить такое распределение памяти для ПМФБ, необходимо поддерживать два дополнительных индекса. Первый должен отслеживать остаток свободного места в каждой строке фильтра. Второй служит для хранения индексов документов, размещенных в каждой строке ПМФБ. На рисунке 1 представлен пример ПМФБ.

Рис. 1. Пример ПМФБ

В этом примере в каждой строке ПМФБ размещено по два документа (T). В строке может быть размещено любое количество документов. Индекс размещения связывает строки фильтра с загруженными текстами документов {T}. Для каждой строки соответствующий индекс определяет документы, которые в ней хранятся. Например, на рисунке 1 показано, что документ хранится в двух строках. Далее в статье будет показано, что в реальных приложениях не будет такого равномерного распределения и многие документы могут быть сохранены в одной строке. Если ФБ’ скомпилированы из документов T’ и имеют определенное сходство с ФБ., мы можем сказать, что текст T’, возможно, схож с одним из документов множества (T), размещенного в ФБ.. В дальнейшем детальное сравнение может подтвердить такое предположение. Это может быть сделано с помощью любого подходящего метода, например по алгоритму Левенштейна. Этап детального сравнения документов выходит за рамки статьи.

Предлагаемая структура данных позволяет относительно легко удалять документ из фильтра без увеличения потребления памяти. Если документ T_i должен быть удален, то только строка (строки) фильтра, содержащая этот документ, должна быть пересоздана.

Так, если в данном примере (см. рис. 1) документ T 1000 был удален из коллекции, то только строки ФБ_h _ 1 и ФБ_h должны быть пересозданы, что является относительно мелкой работой с вычислительной точки зрения. Таким образом, высокая плотность шинглов в строках матрицы дополняется небольшими вычислительными затратами по сравнению с МФБ [17]. Плотность каждого отдельного фильтра в матрице можно оценить с помощью индекса. Фильтры со слабым заполнением могут содержать дополнительные сегменты текста.

Предложенная архитектура имеет следующие важные особенности:

• 1.    Плотность для каждого ФБ. выше по сравнению с ПМФБ, что увеличивает эффективность использования памяти.

• 2.    Увеличение плотности приводит к лучшей вычислительной эффективности структуры данных. При этом важно отметить, что, хотя вычислительная эффективность ФБ остается на уровне 9 ( n * d ), в этой структуре d - это число строк, требуемых для размещения документа, а не полное число документов. Как показал эксперимент, приведенный ниже, количество строк ПМФБ значительно меньше общего количества документов.

• 3.    Количество бинарных проверок прямо пропорционально размеру коллекции { T }.

• 4.    Документ из коллекции удаляется относительно легко.

• 5.    Размер матрицы прямо пропорционален общему числу шинглов в коллекции.

Далее рассмотрена эффективность предложенного подхода, приведен пример расчета размера и плотности фильтра.

Чтобы проверить предложенный подход по использованию ПМФБ, были проведены два эксперимента. Первый был направлен на оценку степени сжатия ПМФБ, второй – на изучение применимости ПМФБ к реальным данным.

Целью первого эксперимента было показать, что на реальных данных размер ПМФБ имеет явное преимущество перед размером МФБ. Для этого были использованы тестовые данные с соревнований по обнаружению плагиата PAN 2009 [18]. Блок данных содержал 14428 документов, содержащих заимствованные куски текста. Среднее количество слов в документе было около 38000. Более 95% документов содержали меньше чем 123000 слов. Представленные в таблице 1 расчеты основаны на следующих утверждениях:

• 1.    Текстовые шинглы (фразы из нескольких слов) были составлены из слов методом «скользящего окна», и их количество приблизительно равно количеству слов в тексте. Само количество слов в шингле может влиять на степень детализации поиска в ПМФБ, но этот вопрос выходит за рамки данной статьи.

• 2.    Последовательность размещения документов в фильтре не влияет на его емкость. На практике данное утверждение не совсем верно, так как если случайные документы постоянно добавляются и удаляются в/из ПМФБ, это приводит к фрагментации индекса, тем самым снижается его поисковая производительность. Вопрос может быть решен путем создания некоторого порога для коротких шинглов при размещении в пустых строках фильтра.

Таблица 1

Размер фильтра и операции над блоком тестовых данных

Значения	Пояснения
p = 0,05	Степень приемлемого риска ложноположительных срабатываний равна 5%
n = 123000	В фильтре такого размера разместится более 95% документов. Если текст документа имеет более чем 123000 слов, то он будет помещен в несколько строк фильтра. Если менее, то свободное место в строках будет занято текстом из других документов
m = 766,933 бит	См. формулу (2), 766933 бит – около 94 Кб
d = 4489	Общее количество строк в ПМФБ равно отношению общего количества слов в блоке к количеству слов в строке
M ~ 411 Мб	Общий размер ПМФБ для размещения всех 14428 документов блока

Из таблицы 1 видно, что при размещении в ПМФБ информация сжата в пропорции 1:3,2 по сравнению с МФБ. При простой реализации МФБ в матрице понадобится 14428 строк вместо 4489. Кроме того, около 5% документов не попали бы в одну строку матрицы и исчезли бы из области поиска. Увеличение размера матрицы до самого большого документа в корпусе (~ 428000 слов) приведет к увеличению размера МФБ в 4 раза.

Степень сжатия 1:3,2 также показывает, что 95% документов распределены в одной или двух строках матрицы. Такое распределение позволяет считать, что в случае удаления документа из фильтра необходимо будет пересоздать только одну или две строки матрицы. Здесь же возникает вопрос повторного использования пространства. Мы можем предложить алгоритмы, аналогичные алгоритмам «сборки мусора», которые позаботятся об освободившемся пространстве после того, как документ был удален из ПМФБ. Процедуру заполнения такого пространства можно производить в интервал времени, когда операции поиска в системе могут быть отложены.

Очевидно, что повышение плотности размещения в фильтре улучшает эффективность сравнения. И если найдено сходство ФБ’ и ФБ_i , то соответствующий текст T’ и T_i следует сравнивать более подробно. В случае ПМФБ сходство ФБ’ и ФБ_i означает, что текст T’ должен быть сравнен с более чем одним документом. В соответствии с приведенным выше примером в 95% случаев в среднем T’ должен быть сравнен минимум с 4 документами и максимум с 8 документами, так как 95% документов размещены по одной или двум строкам матрицы. Таким образом, с одной стороны, с увеличением длины строки матрицы n улучшается сжатие, но, с другой стороны, это увеличивает нагрузку на компоненты системы, которые будут выполнять детальное сравнение.

Целью второго эксперимента была проверка применимости ПМФБ для обнаружения сходства текстов. Для сравнения были использованы два множества. Первое множество состояло из 500 документов, в текст которых были произведены вставки текста из 50 различных документарных источников. Каждая вставка была взята только из одного из 50 источников и размещена внутри документа случайным образом. Все документы содержали примерно около 4000 слов. В связи с тем что все тестовые документы в данном блоке имели одинаковое количество слов, не было как такового сжатия данных с использованием технологии ПМФБ и каждый из документов был помещен в отдельную строку матрицы. Каждый из 50 исходных документов сравнивался со всеми 500 документами тестового блока. Уровень сходства оценивался количеством единиц в одинаковых позициях одной строки [19]. Ожидалось увидеть некоторое сходство среди совершенно разных документов, так как фильтры Блума способны иметь некоторый уровень ложных срабатываний. Интересовал вопрос о том, что фактические вставки текста производят более высокий уровень сходства по сравнению с общим фоновым уровнем. Эксперимент подтвердил это утверждение для всех 50 источников. Если в документах находилась часть исходного текста, то эти части имели отличительные всплески на графике уровня сходства. Пример такого графика для одного из источников представлен на рисунке 2. На нем показано 10 различных уровней сходства для 10 источников. Крайний левый пик графика соответствует 5%-й вставке исходного текста из документа, правый – 50%-й вставке. На основе результатов этого эксперимента мы можем утверждать, что ПМФБ подходит для предварительного сравнения текстовых документов, если часть текста документов (5% и более) была без изменения скопирована из какого-либо источника.

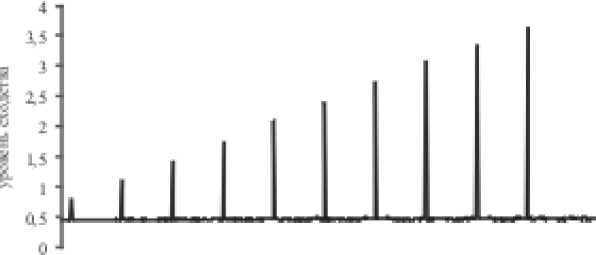
конф .veyirane

Рис. 2. Пример сравнения исходного документа с блоком из 500 документов

Третий эксперимент был проведен на большом блоке тестовых текстов для оценки уровня ложноположительных и ложноотрицательных срабатываний. Для оценки эффективности ПМФБ были использованы тестовые данные для соревнований по обнаружению плагиата PAN 2009 [20]. Хотя классический фильтр Блума склонен к ложноотрицательным срабатываниям, ПМФБ может вести себя по-другому. Документ максимального размера – в уравнениях (1) и (2) это значение n – при размещении в битовой строке будет представлен максимальным количеством шинглов. Но фактически, чтобы оценить все возможные комбинации в одной строке, необходимо рассмотреть все возможные шинглы. Например, если брать шингл, состоящий из трех слов, то общий объем n будет состоять из возможных троек слов документа, т.е. по документу, состоящему из 104 слов, возможно сгенерировать 1012 всевозможных комбинаций. Поэтому рассмотрение n как максимально возможного количества шинглов в документе увеличивает ложноположительные срабатывания. Это, в свою очередь, приведет к увеличению ложноотрицательных срабатываний, а менее строгие критерии сравнения будут использованы для уменьшения количества ложноположительных срабатываний.

Блок тестовых данных PAN 2009 содержал 14428 документов, из которых 3607 имели вставки заимствованного текста – плагиат [21]. Количество операций сравнения для всех документов тестового блока – около (14 * 103 * 14 * 103) /2 ~ 108. В процессе сравнения были использованы два подхода для заполнения ПМФБ. При первом подходе документы располагались в строках, причем документы помещались целиком и в строке могло быть размещено несколько документов. При втором подходе – документы, по длине не поместившиеся в одну строку, располагались в нескольких строках матрицы. В таблице 2 показано, что увеличение плотности документов в матрице привело к уменьшению ложноположительных срабатываний, но количество ложноотрицательных срабатываний увеличилось вдвое. Кроме того, при втором подходе строки фильтра были заполнены только на 50% от своей емкости, что в результате снизило показатель ложноположительных срабатываний. И в том и другом подходе имеется некоторое количество ложноотрицательных срабатываний. Анализ этих срабатываний показал, что все они были связаны с документами, которые содержали менее 1% текста, заимствованного из исходных документов. Кроме того, в 26 документах из 117, по которым были ложноотрицательные срабатывания, вставленный текст был модифицирован, с учетом того что сравнение производилось на уровне слов, такие результаты можно считать ожидаемыми. Результаты с ложноположительными срабатываниями в обоих подходах разнятся. Наблюдается значительное уменьшение количества ложноположительных срабатываний при уменьшении плотности размещения текста в строках матрицы на 50%. Эту особенность можно использовать при разработке инструментов сравнения текстов. Если имеется возможность предоставить ПМФБ двойной размер памяти, то значительно снизится нагрузка на второй этап с детальным сравнением документов.

Таблица 2

Результаты различных способов размещения текста документа в ПМФБ

Результат	Количество срабатываний при размещении текста, шт. (%)
	в одной строке	в нескольких строках
Ложноположительное срабатывание (от общего числа возможных попарных сравнений)	301977 (~0,31%)	9322 (~0,01%)
Ложноотрицательное срабатывание (от общего числа документов с плагиатом)	51 (~1,5%)	117 (~3%)

Проведенные эксперименты показали, что ПМФБ может быть использован в системах быстрого сравнения текстов для фильтрации большого объема документов, но при этом возможны пропуски модифицированного текста.

Одним из возможных направлений улучшения качества работы предложенной структуры данных является использование методов распознавания стиля документа (стилеметрии) [22] для снижения объема шинглов, загружаемых в ФБ. В этом случае стилевые характеристики позволят определить неоднородность текста и выбрать ограниченное число шинглов в ФБ. Дополнительная компрессия, выполненная подобным образом, должна снизить объем памяти, требуемый для ПМФБ, и, как следствие, увеличить скорость сравнения. Чтобы установить, насколько этот подход повлияет на качество определения схожих фрагментов, требуется провести дополнительные эксперименты.

Таким образом, для быстрого сравнения документов предлагается использовать структуру данных, основанную на идее, реализованной в фильтре Блума. Предложенные структура данных и алгоритмы их обработки позволяют эффектив- нее использовать память, а дополнительный индекс дает возможность находить потенциально похожие документы, даже если они были размещены в одной строке фильтра. Этот индекс также позволяет улучшить проведение операции удаления документов из фильтра.

Предложенный подход имеет ограничение, связанное с тем, что быстрое побитовое сравнение возможно только в операционной памяти вычислительной системы: весь фильтр должен быть в памяти компьютера. Даже при частичном размещении фильтра на дисковом пространстве теряются все его скоростные преимущества. На основе эксперимента, описанного выше, можно констатировать, что даже минимальная конфигурация серверного оборудования с несколькими гигабайтами оперативной памяти позволяет обрабатывать сотни тысяч документов. Первый эксперимент показал заметное преимущество размера псевдо-матричного фильтра Блума (ПМФБ) над размером соответствующего матричного фильтра Блума. Результаты второго эксперимента показали применимость ПМФБ-подхода для фильтрации текстов, содержащих 5% (и более) заимствованного текста.

• 1.    Knuth D., Morris Jr.J., Pratt V. Fast Pattern Matching in Strings // SIAM Journal on Computing. 1977. №6 (2). Р. 323–350.

• 2.    Brin S., Davis J., García-Molina H. Copy detection mechanisms for digital documents // SIGMOD Rec. 1995. №24 (2). Р. 398–409.

• 3.    Cormack G.V. Email Spam Filtering: A Systematic Review // Found. Trends Inf. Retr. 2008. №1 (4). Р. 335–455.

• 4.    Butakov S., Scherbinin V. The toolbox for local and global plagiarism detection // Comput. Educ. 2009. №52 (4) Р. 781–788.

• 5.    Bloom B.H. Space/time trade-offs in hash coding with allowable errors // Commun. ACM. 1970. №13 (7). Р. 422–426.

• 6.    Федотов А.М., Барахнин В.Б. К вопросу о поиске документов «по аналогии» // Вестник Новосибирского государственного университета. Серия: Информационные технологии. 2009. Вып. 4. Т. 7. С. 5–7.

• 7.    Bloom B.H. Op. cit.

• 8.    Ibid.

• 9.    Broder A., Mitzenmacher M. Network Applications of Bloom Filters: A Survey // Internet Mathematics. 2005. №1 (4). P. 485–509.

• 10.    Fan L., Cao P., Almeida J., Broder A. Summary cache: a scalable wide-area web cache sharing protocol. IEEE/ACM Trans. on Networking. 2000. №8 (3). Р. 281–293.

• 11.    Guo D., Wu J., Chen H., Luo X. Theory and Network Applications of Dynamic Bloom Filters // INFOCOM 2006. 25th IEEE International Conference on Computer Communications. Proceedings. 2006. Р. 1–12,

• 12.    Karp R.M., Rabin M.O. Pattern-matching algorithms // IBM Journal of Research and Development. 1987. №31 (2). Р. 249–260.

• 13.    Schleimer S., Wilkerson D., Aiken A. Winnowing: Local Algorithms for Document Fingerprinting // Proceedings of the ACM SIGMOD International Conference on Management of Data. 2003. P. 76–85.

• 14.    Geravand S., Ahmadi M. A Novel Adjustable Matrix Bloom Filter-Based Copy Detection System for Digital Libraries // 11th IEEE International Conference on Computer and Information Technology. CIT 2011. Proceedings. P. 518–525.

• 15.    Ibid.

• 16.    Bloom B.H. Op. cit.

• 17.    Geravand S., Ahmadi M. Op. cit.

• 18.    Potthast M., Eiselt A., Stein B., Barrón-Cedeño A., Rosso P. PAN Plagiarism Corpus PAN-PC-09. URL: http://www.uni-weimar.de/medien/webis/research/corpora .

• 19.    Geravand S., Ahmadi M. Op. cit.

• 20.    Schleimer S., Wilkerson D., Aiken A. Op. cit.

• 21.    Ibid.

• 22.    Stamatatos E. A survey of modern authorship attribution methods. J. Am. Soc. Inf. Sci. 2009. №60 (3). P. 538–556.