Пучки Фурье-Бесселя с конечной энергией

Большое внимание в оптике уделяют инвариантным к распространению световым пучкам, которые распространяются в свободном пространстве или в оптической системе, сохраняя свою поперечную структуру (вплоть до масштаба и поворота).

Среди пучков, которые распространяются без дифракции, наиболее известны пучки Бесселя [1], пучки Матье [2] и параболические пучки [3]. Все они представляют собой решение непараксиального уравнения Гельмгольца, обладают бесконечной энергией и вследствие этого могут быть сгенерированы только приближенно. Например, пучки Бесселя обычно генерируются с помощью аксикона [4, 5], в то время как их изображения в дальней зоне (идеальные оптические вихри), как это было показано в [6], лучше формируются с использованием другого фазового элемента. В том же 1987 году, когда были открыты пучки Бесселя, были предложены пучки Бесселя– Гаусса [7], обладающие конечной энергией. Как пучки Бесселя, так и пучки Бесселя–Гаусса не являются Фурье – инвариантными, поскольку преобразование Фурье – пучков Бесселя дает кольцевую дельтафункцию Дирака, тогда как преобразование Фурье – пучков Бесселя–Гаусса описывается модифицированной функцией Бесселя. Позже появились различные семейства вихревых пучков, амплитуда которых пропорциональна функции Бесселя. К этим семействам относятся пучки Бесселя с квадратичной радиальной зависимостью [8], обобщенные пучки Бессе- ля–Гаусса [9], пучки Ханкеля–Бесселя [10], асимметричные пучки Бесселя [11] и Бесселя–Гаусса [12] или дробные пучки Бесселя [13]. Однако все перечисленные выше типы пучков Бесселя [1,7 – 13] не являются Фурье-инвариантными. В [14] описаны не изменяющиеся по форме бесселевы пучки (в том числе высокого порядка), которые экспериментально генерировались из Гауссова пучка с помощью двух аксиконов.

Параксиальное распространение в свободном пространстве и в оптических системах обычно описывается некоторыми интегральными преобразованиями, такими как преобразование Френеля, ABCD-преобразование или преобразование Фурье. Последнее описывает распространение от передней фокальной плоскости тонкой сферической линзы к задней фокальной плоскости. Для невихревых полей собственные функции указанных линейных канонических преобразований подробно исследованы в [15]. Среди оптических вихрей наиболее известным Фурье-инвариантным полем является пучок Лагерра–Гаусса (ЛГ) [16]. Обычные пучки ЛГ имеют широкую темную область в центре. Это создает ряд проблем в задачах интерферометрии, где требуются пучки с более узким темным пятном. Такие пучки также можно использовать для эффективного вращения металлических (поглощающих) частиц, поскольку такие микрочастицы захватываются в центральную темную область.

В этой работе мы аналитически описываем световое поле, которое инвариантно к преобразованию Фурье, содержит оптический вихрь и имеет слабые боковые лепестки. Это поле удовлетворяет паракси- альному волновому уравнению. Однако его комплекснозначная амплитуда найдена только в зоне дифракции Фраунгофера. Этот пучок имеет конечную энергию, хотя и не обладает Гауссовой огибающей. По мнению авторов, в данной работе впервые продемонстрирован пучок с конечной энергией, комплексная амплитуда которого содержит только функцию Бесселя и амплитудный множитель (степень от радиальной полярной координаты). Отметим, что радиальное распределение комплексной амплитуды найденного пучка пропорционально функции Бесселя дробного порядка. Если сравнивать с полуцелыми бесселевыми пучками [13], представленные пучки Бесселя дробного порядка описываются функцией Бесселя, имеющей порядок нечетного целого числа, деленного на 6. Главное геометрическое отличие предложенных пучков Бесселя дробных порядков от мод ЛГ с нулевым радиальным номером заключается в том, что темное пятно первых меньше. А основное отличие от бездифракционных бесселевидных пучков [14] – слабые боковые лепестки.

Вычисляя интеграл по φ, мы получим:

E 2 ^{( p} , 9 ) = ⁽ - i ) ^{m +1} _{f a} ^k + i_{)Z 6} exp ⁽ im о )^х

да v    (2-m)/3 T

^X J ^r        J ( 2 m - 1)/6

( a r ² ) exp ( i a r ² ) J_m

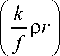
dr .

В [18] есть интеграл (выражение 2.12.40.15):

да

J x < ^2-v)/³

sin bx ² cos bx ²

J ( _{2 v- 1})/6 ( bx ² ) J v ( cx ) dx

= ( 4 b ) ^(v-2)/3 c '^{: 3}

sin ф cos ф

^J ( 2 V- ¹)/⁶

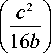
где b , c >0, Re ν >–(7±3)/4 и

y = (v +1)---.                                   (6)

616 b

Используя этот интеграл, из уравнения (4) получим:

Амплитуда пучков Фурье–Бесселя

Пусть исходное поле в начальной плоскости (передняя фокальная плоскость сферической линзы) имеет следующую комплексную амплитуду:

E i ( r , ф ) = (7 а r )

- ( m + 1 )/3

X

^{X J} ( 2 m - 1)/6 ( ^a r 2 ) exP ( i « r 2 ⁺ im ф ) ,

где ( r , φ) – полярные координаты, m – топологический заряд оптического вихря, α – коэффициент масштабирования. Заметим, что в отличие от известных радиально-симметричных оптических вихрей m -го порядка, вблизи оптической оси комплексная амплитуда не возрастает, как r^m . Ниже мы получим дополнительное условие для порядка вихря m .

Согласно [17], в дальней зоне (задняя фокальная плоскость сферической линзы) комплексная амплитуда имеет вид:

• i да 2 n

E2 (p, 9) ' J J Ei (r, ф)х 2nf 00

x exp

- if p r cos ( ф-9 ) | rdrd ф ,

где ( ρ, θ) – полярные координаты в дальней зоне, k =2π / λ – волновое число света с длиной волны λ, f – фокусное расстояние линзы.

Подставляя (1) в (2), получим:

E 2 ⁽ p , ^{9 )}=^ i7 fj(^ r ) ^{( V} J ( 2 m - 1 )/ 6 ^(a r ^{2 )X 2 n f} 0 0

x exp | i a r ² + im ф- if p r cos ( ф-б ) | rdrd ф .

x exp

r ikp_ I 16 a f ²

E 2 ( p , 9 ) = i ^{-2( m + 1 ) 3}

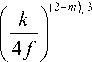
_a( m - ^{5 )} 6 p ^-( m + ¹)/ 3

⁺ im ⁹ I ^J ( 2 m - 1)/6

r 22pL)

I 16 a f ² )

Согласно уравнениям (1) и (7), входное и выходное поля имеют одинаковую осесимметричную структуру интенсивности:

I (r, ф) = E (r, ф)|2~ ^m+1V3J(22m-1),6 (^) , где ξ = βr2, а β – некоторое действительное число. Из уравнений (1) и (7) также можно видеть, что если α = k /(4f ), то входной и выходной пучки имеют одинаковый радиус.

В некоторых специальных случаях, когда, например, m =2, 5, 8, 11, ..., функция Бесселя приобретает полуцелый порядок, и комплексная амплитуда может быть выражена через элементарные функции. Например, при m =2:

E 1 ( r , ф ) = V2/ n ^- 1 sin ^ 1 exp ( i ^ 1 + 2 i ф ) , k

E 2 ( p , 9 ) = ——§₂ 1 sin ^ 2 exp ( - i ^ 2 + 2 i 9 ) ,

V 8 n f a где

^ 1 =a r ² ,

^2 = k^— .

² 16 a f²

Стоит отметить, однако, что Фурье-инвариантное распределение, полученное из уравнений (1) и (7), имеет недостаток. Комплексная амплитуда светового поля должна быть непрерывной. Чтобы избежать сингулярности при r =0, топологический заряд дол-

жен удовлетворять условию m ≥ 2. Однако из формул (8) и (9) видно, что даже при m =2 существует вихрь 2-го порядка без нуля интенсивности, так как комплексные амплитуды (8), (9) вблизи оптической оси имеют вид:

E1 (r ^ 0, ф) = ^2/n exp (iar2 + 2iф),

E 2 ( p^ 0, 0 ) =

k        f ik ² p ²

exp I -—V8nfa   ( 16af2

+ 2 i 0

Кроме того, не только само поле, но и его производная также должна быть непрерывной (поскольку магнитное поле должно быть непрерывным). Выражение для ∂ E / ∂ r довольно громоздко, и здесь оно не приведено, но оно показывает, что для исключения сингулярности (без нулевой интенсивности) мы должны полагать, что m ≥ 5. При m =5 комплексная амплитуда может быть записана следующим образом:

E 1 ( r , ф ) = 72/П - 5 2 x x ( sin ^ 1 -^ 1 cos ^ 1 ) exp ( i ^ 1 + 5 i ф ) ,

E2 (p,0)= V5fx x(sin ^2 -^2 cos -;) exp (-i§2 + 5i0), где ξ1 и ξ2 определены в (10) и (11).

Энергия мод Фурье–Бесселя дробного порядка

Получим выражение для энергии предложенных пучков. Уравнение (7) можно переписать в виде:

E ₂ ( p , 0 ) = i 2 m ⁺¹⁾/³ — x

4 a f                         (14)

■- m+1V6 exp (-i _. im 0) J(2 m _,)/6 (10, где ξ определяется как ξ2 в (11):

^ = k ² p ² /( 16 a f ² ) .                                (15)

Таким образом, энергия пучка определяется выражением

W = J j|Eг (p,0)|2 pdpd0 = да

^J^ m ^+1)/3 J 22 m - 1)/6 (^) d ^

^a 0

Используя справочный интеграл (выражение

2.12.31.2 в [18]), получаем энергию пучка:

W =

г/m +1 / n32             ( 6 J 1

3    m2 rCmi^ If! m+4 Iff m+5 la

¹1 6 H 6 H 6 ^J

Таким образом, в отличие от обычных бездифрак-ционных пучков Бесселя, энергия пучков Фурье– Бесселя дробных порядков конечна.

Моделирование

Ширина пучка

В этом параграфе мы сравниваем пучки Фурье– Бесселя дробного порядка с хорошо известными модами ЛГ, которые сохраняются при распространении в пространстве и, в частности, в дальней зоне. В исходной плоскости комплексная амплитуда моды ЛГ (в полярных координатах) имеет вид:

f V2 r 1 m

E 1 ( r , ф )= ----

V ^W 1 ^J

r f 2 r21 f r2Lmp \ —— I expl--- + im ф

V w 1² J    V w 12

где w 1 – радиус перетяжки Гауссова пучка, m и p – азимутальный (топологический заряд) и радиальный индексы моды соответственно. Далее мы полагаем радиальный индекс p равным нулю, чтобы избежать периферийных световых колец (так как пучки Фурье– Бесселя, как будет показано ниже, имеют в начальной плоскости и в дальней зоне одно световое кольцо почти без боковых лепестков). Когда такой пучок падает на сферическую линзу, то в фокальной плоскости, применяя преобразование Фурье, мы получим следующее распределение амплитуды:

m

( J^1          2 2

E2 (p, 0) = (-i) I — I ---- x expl-2- + im0|, (19)V f JV W2 J V w2      J где f – фокусное расстояние линзы, а

Zr = kw ¹- , W 2 = W 1 f . (20) 2 z R

На рис. 1 показаны распределения интенсивности и фазы пучков Фурье–Бесселя дробного порядка и мод ЛГ в начальной плоскости (передняя фокальная плоскость линзы) и в дальней зоне (задняя фокальная плоскость линзы). В ходе моделирования использовались следующие параметры: длина волны λ = 532 нм, фокусное расстояние линзы f = 1 м, топологический заряд оптического вихря m =5. Коэффициент масштабирования моды Фурье–Бесселя дробного порядка и радиус перетяжки моды ЛГ соответственно равны α = k /(4 f ) ≈ 2,95 мм ^–2 и w 1 =(2 f / k )^1/2 ≈ 411 мкм. При этих значениях размер пучка в выходной плоскости точно такой же, как в исходной. Размер расчетной области R =2 мм (– R ≤ x , y ≤ R) . Распределения интенсивности и фазы в начальной плоскости были рассчитаны с использованием формул (1) и (18), тогда как распределения интенсивности в выходной плоскости были получены с использованием преобразования Френеля, реализованного в виде свертки с применением алгоритма быстрого преобразования Фурье.

Как видно из рис. 1, распределения интенсивности в выходной плоскости действительно выглядят очень похожими на распределения во входной плоскости, хотя они были получены численно с помощью двух преобразований Френеля, а не по формулам (7) и (19). Оба пучка имеют поперечную интенсивность в виде светового кольца, в то время как распределение их фаз кардинально отличается. В то время как мода ЛГ содержит только фазу вихря, пучок Фурье–Бесселя дробного порядка дополнительно имеет фазу, подобную параболической линзе. Также видно, что световое кольцо пучка Фурье–Бесселя намного толще, вследствие чего внутреннее темное пятно меньше. Ширина кольца по полуспаду интенсивности у пучка Фурье–Бесселя составляет 624 мкм, тогда как световое кольцо ЛГ имеет ширину 340 мкм, т.е. почти вдвое уже. У моды ЛГ боковые лепестки отсутствуют, в то время как у пучка Фурье–Бесселя дробного порядка боковые лепестки составляют 4,6% от максимальной интенсивности.

е)

Рис. 1. Распределение интенсивности (а, в, д, е) и фазы (б, г) пучка Фурье–Бесселя дробного порядка (а, б, е) и моды ЛГ (в, г, д) в исходной плоскости (передняя фокальная плоскость линзы) (а – г) и в дальней зоне (задняя фокальная плоскость линзы) (д, е)

г)

Расходимость пучка

Дополнительно была изучена расходимость обоих видов пучков. Параметры были выбраны так, чтобы пучок Фурье–Бесселя дробного порядка и мода ЛГ имели одинаковый радиус кольца в исходной плоскости: 1 мм. На рис. 2 показаны распределения интенсивности пучка Фурье–Бесселя и моды ЛГ в передней и задней фокальных плоскостях тонкой линзы. В процессе моделирования были использованы следующие параметры: длина волны λ =532 нм, фокусное расстояние линзы f = 1 м, топологический заряд оптического вихря m = 5. Коэффициент масштабирования моды Фурье–Бесселя дробного порядка и радиус перетяжки моды ЛГ соответственно равны α≈ 1,526 мм –2 и w1 ≈ 633 мкм (такие α и w1 позволяют получить радиус кольца распределения интенсивности r1 = 1 мм в исходной плоскости). Размер расчетной области R =3 мм (– R ≤ x, y ≤ R). Распределения интенсивности в начальной плоскости были рассчитаны с использованием формул (1) и (18), тогда как распределения интенсивности в выходной плоскости мы получили с помощью формул (7) и (19).

Рис.

плоскости (передняя фокальная плоскость линзы) (а, в) и в дальней зоне (задняя фокальная плоскость линзы) (б, г)

На рис. 3 показаны сечения пучка Фурье–Бесселя и моды ЛГ в передней и задней фокальных плоско- стях линзы.

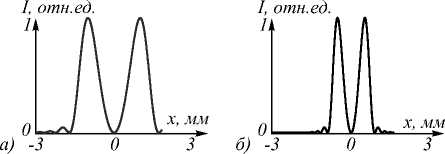
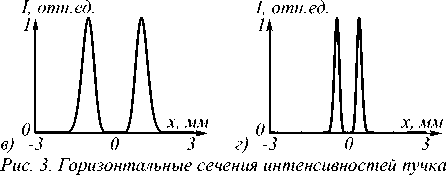
Фурье–Бесселя дробного порядка (а, б) и моды ЛГ (в, г)

в исходной плоскости (передняя фокальная плоскость линзы) (а, в) и в дальней зоне (задняя фокальная плоскость линзы) (б, г)

Как показывает численное моделирование (рис. 2–3), в дальней зоне (задняя фокальная плоскость) для пучка Фурье–Бесселя радиус максимальной интенсивности на 22 % больше ( r 2 ≈ 516 мкм), чем для моды ЛГ (r 2 ≈ 422 мкм). Как и на рис. 1, световое кольцо пучка Фурье–Бесселя на рис. 2 намного толще, чем у моды ЛГ. Ширина по полуспаду интенсивности составила 404 мкм и 223 мкм соответственно.

Мы дополнительно измерили диаметр по полу- спаду интенсивности внутреннего темного пятна во входной плоскости (рис. 3а, в), где радиус кольца обоих пучков одинаков. Он составил 1,14 мм и 1,5 мм для пучка Фурье–Бесселя и моды ЛГ соответственно.

Таким образом, для пучка Фурье–Бесселя дробного порядка площадь темного пятна почти в два раза меньше (58 %). Даже в задней фокальной плоскости (рис. 3 б , г ), несмотря на больший радиус кольца пучка Фурье– Бесселя, диаметр его темного пятна меньше, чем у моды ЛГ (592 мкм и 634 мкм соответственно).

Разница в размере радиуса светового кольца пучка Фурье–Бесселя и моды ЛГ может быть объяснена теоретически исходя из используемых формул. Согласно (18) и (19) радиальная зависимость амплитуды моды ЛГ вблизи центра равна | E | ~ r^m . Уравнения (1) и (7) показывают, что для пучка Фурье–Бесселя дробного порядка | E | ~ r ^{( m – 2)/3}. Это означает, что при r << 1 интенсивность вблизи центра для пучка Фурье– Бесселя растет намного быстрее, чем для моды ЛГ.

Распространение пучка Фурье–Бесселя в свободном пространстве

Чтобы проследить динамику распространения пучка Фурье–Бесселя в свободном пространстве, надо от поля (1) вычислить преобразование Френеля. В отличие от преобразования Фурье, использование которого позволило получить распределение комплексной амплитуды в дальней зоне (7), мы не смогли это сделать аналитически и в данном параграфе приводим численные результаты расчёта распределения интен- сивности в нескольких поперечных плоскостях. На рис.4 показаны эти распределения для следующих параметров расчёта: длина волны λ =532 нм, топологический заряд оптического вихря m =5, масштабирующий множитель пучка Фурье–Бесселя α≈ 1,526 мм –2 (в этом случае радиус кольца в начальной плоскости равен 1 мм), расстояния распространения 0, 0,5 м, 1 м, 3 м, 5 м, 10 м, 30 м, и 50 м. Расчётная область – R ≤ x, y ≤ R, где R =3 мм (z =0 и z =0,5 м), R =4 мм (z = 1 м), R =5 мм (z =3 м), R = 10 мм (z =5 м), R =20 мм (z = 10 м), R =50 мм (z =30 м), R =75 мм (z =50 м).

Из рис. 4 видно, что пучок Фурье–Бесселя не модовый и его поперечное сечение при распространении меняется. Несмотря на форму широкого кольца в начальной плоскости (рис. 4 а ), в некоторых других плоскостях распределение интенсивности состоит из нескольких колец, и даже в тех плоскостях, где кольцо одно (рис. 4 г ), относительная ширина кольца (ширина кольца, делённая на его радиус) намного меньше, чем в начальной плоскости. При дальнейшем распространении, однако, в дальней зоне распределение интенсивности снова приобретает форму (с точностью до масштаба), в точности совпадающую с формой в начальной плоскости (рис. 4 з ).

а)

д)

б)

е)

1 мм

в)

ж)

г)

з)

Рис. 4. Распределения интенсивности пучка Фурье–Бесселя в нескольких поперечных плоскостях, расположенных на расстояниях z=0 (начальная плоскость) (а), 0,5 м (б), 1 м (в), 3 м (г), 5 м (д), 10 м (ж), 30 м (ж), 50 м (з)

Заключение

В этой работе мы рассмотрели световые пучки Фурье–Бесселя дробного порядка, которые содержат оптический вихрь, имеют слабые боковые лепестки и инвариантны к преобразованию Фурье. Все другие известные пучки Бесселя не являются Фурье-инвариантными. Радиальное распределение комплексной амплитуды данных пучков пропорционально функции Бесселя дробного порядка (нечетное целое число, деленное на 6). Эти пучки имеют конечную энергию и при этом не обладают Гауссовой огибающей. У пучков Фурье–Бесселя дробного порядка внутреннее темное пятно меньше, чем у мод ЛГ с нулевым радиальным номером. Возможные области применения предложенных пучков включают в себя оптическую связь [19], интерферометрию [20] и оптический захват [21].

Работа выполнена при поддержке Российского фонда фундаментальных исследований РФФИ (грант № 18-29-20003) в теоретической части, Российского научного фонда (грант № 18-19-00595) в части моделирования и Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение» и «Заключение».