Пучки Пирси с орбитальным угловым моментом

Вихревые лазерные пучки, обладающие орбитальным угловым моментом, являются объектом пристального внимания в оптике. Они находят применение при уплотнении каналов передачи информации в системах беспроводной связи со скоростью несколько терабит в секунду [1], оптическом захвате и вращении микрочастиц [2], зондировании атмосферы в присутствии турбулентности [3].

Примерами вихревых пучков являются хорошо известные лазерные пучки Бесселя [4], Лагерра– Гаусса [5], гипергеометрические моды [6].

Эти пучки при распространении в пространстве либо сохраняют свою структуру [4], либо масштабно увеличиваются [5,6]. Для применения в задачах микроманипуляции их требуется сфокусировать с помощью микрообъектива. Такая фокусировка неизбежно приводит к искажению формы пучка из-за аберраций фокусирующего объектива. Однако известны лазерные пучки, обладающие свойством автофокусировки. У таких пучков распределение интенсивности в фокусе строго определено. Примерами лазерных пуков с автофокусировкой являются пучки Пирси [7]. В [7] рассмотрены пучки Пирси как трёхмерные аналоги пучков Эйри [8].

Распределение комплексных амплитуд таких пучков описывается функцией Пирси [9, 10], определяемой как интеграл от комплексной экспоненты, аргумент которой является полиномом (подобно функции Эйри).

Угловой спектр таких пучков представляет собой параболу с фазовой модуляцией. Эти пучки обладают свойством автофокусировки и восстанавливаются после искажения препятствиями. В [11] предложен виртуальный источник, формирующий пучок Пирси. В [12, 13] приведено обобщение функции Пирси и рассматриваются структурно-устойчивые половинные пучки Пирси.

Обычные пучки Пирси [7] являются суммой двух половинных пучков Пирси первого порядка. Угловой

спектр половинных пучков Пирси представляет собой не параболу (как у пучков Пирси из [7]), а только одну её половину. Заметим, что пучки Пирси не обладают орбитальным угловым моментом. Также в [12, 13] рассмотрены двумерные аналоги пучков Пирси, обладающие искривлённой траекторией, то есть обладающие ускорением при распространении.

В данной работе на основе двумерных половинных пучков Пирси получены параксиальные вихревые пучки Пирси, обладающие орбитальным угловым моментом. Комплексная амплитуда таких пучков пропорциональна вырожденной гипергеометрической функции, и по форме они совпадают с гипергеометрическими модами [6]. Но так как пучки Пирси обладают свойством автофокусировки, то и полученные здесь вихревые пучки Пирси обладают также свойством автофокусировки.

1. Двумерные половинные пучки Пирси

В этом разделе, следуя [12, 13], кратко рассмотрим двумерные половинные пучки Пирси. Комплексная

амплитуда параксиальных двумерных половинных пучков Пирси в начальной плоскости имеет вид:

+^

E(x,0) = j exp

isp

Г X I

।       । + iS 2p

Y

V x о 7

ds =

= HPe P° ( x/x о ) .

В (1) x – поперечная Декартова координата, продольная координата z в (1) равна нулю, x ₀ – масштабный множитель. С помощью преобразования Френеля можно показать, что на некотором расстоянии z комплексная амплитуда (1) будет равна

+^

E (x, z) = j exp

. n I x I .[.. Z I 2p iSp I I + i I 1--2 I sp

V x о j v   2 kx о j

d s .    (2)

Сделаем замену переменной интегрирования s = (1 – z / z e )^{–1/(2 p )} t , где расстояние автофокуса равно z e = 2 kx 0 ², k – волновое число света. Тогда вместо (2)

получим для комплексной амплитуды двумерного половинного пучка Пирси:

E ( x , z )

x HPe^

= ( 1 - zk 1 ^{( 2} p '

(              A

_____X_____

I x0 (1 - z(ze ) J

.

Замену переменной интегрирования можно делать только для z <  z_e . В противном случае пределы становятся мнимыми. Но из (2) следует, что

E ( x , z e + Q = E * ( ^- x , Z_e ^-Z ) ,                      ⁽⁴⁾

т.е. после прохождения пучка через плоскость автофокусировки z = z_e распределение его интенсивности является зеркальным отражением распределения интенсивности до плоскости z = z_e относительно оптической оси.

Из (4) видно, что в начале распространения (до фокальной плоскости z = z_e ) в любой поперечной плоскости z <  z_e координаты максимумов интенсивности пучка определяются по формуле:

x max = У т ^Х 0 V¹ — ^{( z}K ) , ⁽⁵⁾ где y_m – координата m -го максимума функции |HPe 2 ^ ( x )| 2 . Дважды продифференцировав (5) по z , получим, что при z <  z _e будет выполняться неравенство (d x max /d z )(d² x max /d z ²) > 0, что свидетельствует о наличии ускорения траектории пучка перед фокусировкой. Из свойства симметрии (4) следует, что после прохождения через плоскость z = z _e пучок начнёт распространяться с замедлением.

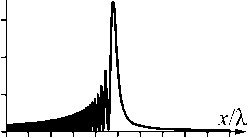
Для примера рассмотрим распространение двумерного половинного пучка Пирси при p =2. Пусть длина волны света равна 1 = 532 нм, масштабный коэффициент в (1) пусть равен x ₀ = 1 . Тогда фокусное расстояние будет равно z e = 4 п1 . На расстоянии z = 3 z_e /4 пучок сужается в два раза, в нашем случае это расстояние равно z = 3 п1 . Максимальная интенсивность при этом увеличивается в два раза. В плоскости z_e = 4 п1 поле (2) «бесконечно» сужается, и возникает автофокус. Для выбранных параметров интенсивность в начальной плоскости имеет вид, показанный на рис. 1 а . Моделирование проводилось конечноразностным методом распространения пучка (BPM-методом) в области -80 1 <  x < 80 1 , 0 <  z < 30 1 . На рис. 1 б показано рассчитанное распределение интенсивности в плоскости Oxz . На рис.1 в,г показаны сечения интенсивности (рис. 1 б ) при z =0 (рис. 1 в ) и z = 75 1 /8 (~3 п1 ) (рис. 1 г ). Из рис. 1 видно, что действительно пучок сузился в два раза: при z =0 координата чётвертого нуля равна примерно -10 1 , а при z = 75 1 /8 она равна примерно -5 1 .

Максимальная интенсивность на рис. 1 г в два раза выше максимальной интенсивности на рис . 1в. Кроме того, видно, что и на рис. 1в, и на рис. 1г интенсивность второго максимума примерно в два раза меньше интенсивности главного максимума, что также демонстрирует изменение светового пучка при распространении только в масштабе, но не в структур е.

z / 1

I, отн. ед.

z e

I, отн. ед.

а) -40 -20 0 20 40

8 0642 в)

б) -20 -10 0 ul, отн. ед.

x / 1

10 20

16-

\bl j^^ ¹

-8 -4 0 4 8

-8 -4 0   4   8

Рис. 1. Распределение интенсивности двумерного половинного пучка Пирси, рассчитанное BPM-методом: сечение интенсивности вдоль оси x при z = 0 (a), интенсивность в плоскости Oxz (негатив)(б), сечения интенсивности вдоль оси x при z = 0 (в)(увеличенная картинка (а)) и при z = 75 X /8 (г)

• 2.    Вихревые пучки Пирси, или гипергеометрические пучки с автофокусировкой

Рассмотрим комплексную амплитуду параксиального трёхмерного монохроматического лазерного пучка, представляющую собой непрерывную суперпозицию двумерных половинных пучков Пирси, каждый из которых повёрнут на полярный угол θ , и у каждого пучка, входящего в суперпозицию, фаза про -порциональна углу поворота n θ:

^E np ( ^x , У , ^z = ⁰ ) =

^(- i ) 2 n

n 2 n

- _J e⁶ * ⁶ d 6

x

^

x J exp

. 7n . n | xcos9+ y sin9 isp + isp I------------------

I       x0

d s ,

где n – целое число, которое называется топологическим зарядом оптического вихря, p – действительное число, задающее порядок половинного пучка Пирси. Заметим, что у обычных пучков Пирси [7] p =2, и интеграл в (6) по переменной s берётся от минус до плюс бесконечности. Пучки (6) с разным топологическим зарядом n ортогональны, а с разным порядком p не ортогональны.

Оба интеграла в (6) можно вычислить, тогда вместо (6) получим:

exp

E np ⁽ r , Ф , z = ⁰⁾ =----

i П [ pn + 1 I x + in Ф

2 I 2 p J

2 pn !

x

n ₂

I pn +1 II r I I pn +1      , . r IXг I          III 1F11  -----, n +1, -i—X I,

I 2p J|2x0 J    | 2p         4x2 J где (r, φ) – полярные координаты, Г(x) – гамма-функция, 1F1(a,b,x) – вырожденная гипергеометрическая функция [14].

С помощью преобразования Френеля можно по-

а суперпозиция (6) в этой плоскости имеет вид (в полярных координатах):

лучить комплексную амплитуду оптического вихря

( - i ) n 2 ⁿ

E np ( r , Ф , z = — e ) = P in d 9^{X 2 n} 0

Пирси (6) на произвольном расстоянии z в виде:

exp

E np ⁽ r , Ф , z ) =

i n

Г pn +1 |I 2 P J

+ in ф

1/2 p

2 pn l l 1 - — I

I ze J

x

X Г | pn+l | £ n F

I 2 P J

Г pn +1

I 2 p

n +1, - i £2

где

£ =----- r----- , — e = 2 kx 0

2 x ₀ 1 - ^— z_e

Можно проверить, что из (8) при z =0 получается (7). Из (8) следует, что при n ≠ 0 на оптической оси ( r =0) при любом z будет нулевая интенсивность, а распределение интенсивности будет иметь вид набора концентрических колец с центром на оптической оси. Но при n =0 пучок (8) не будет вихревым и кольцевым, то есть на оптической оси будет отличная от нуля интенсивность, и комплексная амплитуда будет иметь вид:

^E 0 p ⁽ r, z ) =

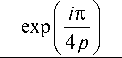
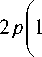
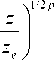
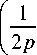
1 F 1

у,1, ^- i ^£ 2 2 p

Комплексная амплитуда (9) описывает параксиальную волну с бесконечной энергией, сходящуюся в точку на оптической оси, аналогично сферической или параболической волнам. Из (8) видно, что при z = z e аргумент ξ стремится к бесконечности. Исполь-

зуя асимптотику при x → ∞

x

n

1 F 1

Г pn +1

I ² p

. .       ■ 2

, n + 1, - ix

^, x

получим, что в плоскости автофокусировки ( z = z e ) комплексная амплитуда (8) пропорциональна

E np ( r , Ф ,— = — . ) . expM.                   (11)

Из (11) следует, что в плоскости автофокусировки ( z = z_e ) формируется острый фокус, но в центре фокуса в одной только точке интенсивность равна нулю (если n ≠ 0). Докажем кратко наличие осевого нуля интенсивности в фокальной плоскости. Согласно (2), комплексная амплитуда двумерного пучка Пирси в фокальной плоскости равна

+^

E ( x , z = — e ) = J exp

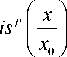
d s ,

™ xj exp is 0 L

_p r cos ( 6-ф ) x ₀

d s ,

Внутренний интеграл на оптической оси ( r =0) равен бесконечности, однако при смене порядка интегрирования получим:

Enp ( r, Ф, z = ze ) =

(-i ) n 2n

^

J dsx

2 n

J

exp in 6 + i

rsp

---cos (6-ф)

x ₀

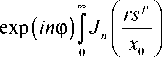
d6=

При r =0 подынтегральное выражение строго равно нулю, а значит, и осевая интенсивность в фокальной плоскости также равна нулю.

Замечательным свойством вихревых пучков Пирси является то, что расстояние автофокусировки z e = 2 kx 2 не зависит от параметров пучка p и n . Это означает, что любая суперпозиция таких пучков с разными номерами p и n будет фокусироваться на том же расстоянии z e . Это свойство вихревых пучков можно использовать для формирования заданного распределения интенсивности и орбитального углового момента в плоскости автофокусировки.

На рис. 2 показаны распределения интенсивности радиального ( n =0) и вихревого ( n =5) пучков Пирси на разных расстояниях от начальной плоскости: z =0 ( а, г ), z = 0,75 z_e ( б, д ) , z = 0,999 z_e ( в, е ). На расстоянии z = 3 z_e /4 картина дифракции сжимается в два раза по сравнению с картиной в плоскости z =0, а на расстоянии z = 0,999 z e – в 10 3 раз. Сечение интенсивности, изображённой на рис. 2 в , показано на рис. 3, ширина

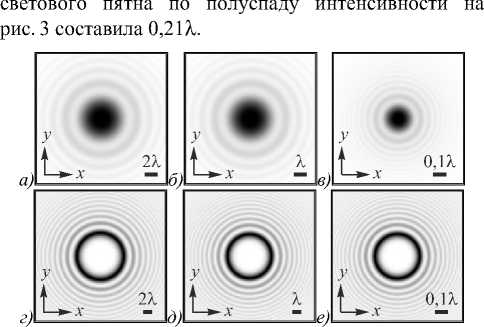
Рис. 2. Распределения интенсивности (негатив) вихревого пучка Пирси при n = 0 (а, б, в) и при n = 5 (г, д, е) в плоскостях z = 0 (а, г), z = 3ze/4 (б, д), z = 0,999ze (в, е)

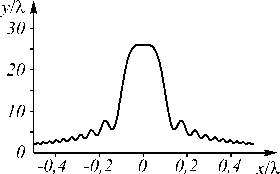
Рис. 3. Сечение интенсивности вблизи фокуса (z=0,999ze) при n=0

Рис. 2 рассчитан по формуле, аналогичной (6):

(-i) n 1

np ⁽ * ^, y ^, z ⁾ = 2 n ( 1 - zjz e ) 1 ^{( 2} p ^)X

x J e in ⁶ HPe 2 D

* cos y sin ⁶ l * oVl ^- zz . J

d 6 ,

при этом использовалось тождество, связывающее функцию Пирси при p = 2 с функцией Бесселя первого рода:

HPe 2 D ( ^ ) =

= -JB exp [- i ^f ^ --11 J_{x /4}^f ^ 1 +          (13)

4 V 2     _ l 8 8 J J 141 8 J л              Г f ^2 3пf^1

⁺Ж ysgn⁽^ exP ^- i I      I ^J 14 I Ж

4 V 2                 l 8    8 J l 8 J

модам (15) в начальной плоскости (при y =0). Заметим, что функция (11) Фурье-инварианта и её Фурье-образ равен

E n ( р , , ) = ( - , ) ^{n + 1}exP ( in ⁶ ) , р> 0.               (16)

р

Но при n + 0 и р =0 амплитуда (16) равна нулю. Можно предположить, что гипергеометрические моды (14) и вихревые пучки Пирси (8) отличаются сдвигом по оптической оси на расстояние автофокусировки. Это косвенно подтверждается методологией получения ускоряющихся пучков из замедляющихся путём смещения вдоль оптической оси [16].

Приравнивая аргумент ξ в (8) к значению, при котором модуль амплитуды достигает максимума ξ ₀ , получим зависимость изменения радиуса кольца с максимальной интенсивностью от расстояния вдоль оптической оси:

Го = 2 * 0 ^ 0 1--.                                   (17)

ze

Из (17) видно, что при z = z e радиус кольца равен нулю. Если, аналогично (5), вычислить первую и вторую производные по z от радиуса кольца (17), то они будут одного знака. Это означает, что вихревой пучок Пирси распространяется до фокуса по ускоряющейся траектории и «круто» сходится в фокус, аналогично кольцевым пучкам Эйри [17].

Это тождество получается из нескольких справочных интегралов (выражения 3.696 в [15]).

Заметим, что вихревые пучки Пирси (8) при p = 1 по структуре совпадают с известными гипергеометрическими модами [6] при у =0:

3. Вихревые пучки Пирси–Гаусса

exp

E n y ( r , Ф , z ) =----

- i n ( n - i Y+ 1 ) + in ф

Пучки (8), как и пучки (14), обладают бесконечной энергией аналогично пучкам Бесселя [4]. Понятно, что если преобразование Френеля от функции (6) вычисляется явным образом с помощью специальных функций (8), то аналогично может быть вычислено преобразование Френеля от функции (6), умноженной на Гауссову

i7, I z xexp ^lnI — _ 2 lz 0 .

x^n/2 F f n - i7+1

¹¹ 1 2

2 п n !

Г f n+iy+1

x

,

,

1/2

Z(> I

— I x z J

где £ = kr 2 /(2 z ), z ₀ = kw 2 /2.

В (14) w – масштабный фактор, аналогичный * ₀ , Y — действительный параметр, аналогичный p . Хотя при p = 1 в (6) имеет место суперпозиция параболических волн, а не обычных пучков Пирси [7] при p =2. Отличие между (8) и (14) ещё в том, что вихревые пучки Пирси (8) в начальной плоскости имеют аналогичный вид (7), а гипергеометрические моды (14) порождаются комплексной амплитудой вида[6]:

E n _Y( ^r , ^Ф , z = ⁰ )

1 f w

2 n l r

exp

( r I i yln I — I + in ф l w J

Сравнивая (11) и (15), видно, что вихревые пучки Пирси (8) в плоскости автофокуса (Фурье-плоскость) имеют вид (11), аналогичный гипергеометрическим

экспоненту. Поэтому рассмотрим вихревые пучки Пирси–Гаусса в начальной плоскости, умножив комплексную амплитуду (6) на Гауссову экспоненту:

( - i ) ⁿ

F np ( * , У , z = 0) = exp ^p               2 n

2 п       ^

x J e ' ^{n 6} d 6 j exp is ^{2 p} + is

0           0        _

^^^^^^в

2     2 Л

* ² + у ² I

Jx

_p J * cos 6 + у sin 6

l        * 0

(18) d s ,

где σ – радиус перетяжки Гауссова пучка.

Комплексная амплитуда вихревых пучков Пирси– Гаусса на произвольном расстоянии от начальной плоскости получается с помощью преобразования Френеля и равна:

^F np ^{( r} , Ф , ^z ) =

x exp

exp

i

-—( n + 1) + in Ф

2 pn

x

r ²        ikr ²

+

O ² ( z ) 2 R ( z )

g ^{(1 - 2 p} )/ ^p ( z ) q -¹/ ^p ( z ) x

x Г I pn + 1 1 ^ n 1 F 1 1 pn + 1 l 2 p J l 2 p

n +1, - i^

где

s=

r

2 x ₀ g ( z ) q ( z ) ,

g ( z ) =

z

z ₀

i ,

q ( z )

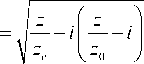
k o ²

o( z) = o

7                      7,

1 + — , R (z) = z I 1 + -2

z ₀

z

При σ → ∞ амплитуда (19) переходит в (8). Заметим, что произведение g ( z ) q ( z ) в знаменателе аргумента ξ является комплексным числом и не равно нулю ни при каком z . При z = z_e модуль произведения g ( z ) q ( z ) достигает минимума. То есть в отличие от вихревых пучков Пирси (8), у вихревых пучков Пирси–Гаусса (19) в плоскости автофокусировки радиус пучка минимальный, но отличен от нуля. Но при этом вихревые пучки Пирси–Гаусса обладают конечной энергией и могут быть сформированы с помощью жидкокристаллического модулятора света.

Заметим также, что пучки (19) при p = 1 и при z_e → ∞ по своей структуре совпадают с гипергеометрическими пучками [18] при m =-1, у =0. Но пучки в [18] не обладают свойством автофокусировки.

Заключение

В работе получены следующие результаты:

– получено новое решение параксиального уравнения Гельмгольца (уравнения типа Шредингера), описывающее двухпараметрическое семейство структурноустойчивых трёхмерных вихревых пучков Пирси (уравнение (8));

– показано, что комплексная амплитуда вихревого пучка Пирси по структуре совпадает с комплексной амплитудой гипергеометрических мод [6], но в отличие от них обладает свойством автофокусировки;

– вихревой пучок Пирси распространяется до фокуса по ускоряющейся траектории и «круто» сходится в фокус аналогично кольцевым пучкам Эйри [16];

– получено также явное выражение для комплексной амплитуды вихревых пучков Пирси–Гаусса (уравнение (19)) с конечной энергией, которые обладают свойством автофокусироки, но радиус пучка в фокусе конечен, в отличие от вихревых пучков Пирси с бесконечной энергией, у которых радиус пучка в фокусе равен нулю.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9), а также грантов РФФИ 13-07-97008, 14-29-07133, 1407-31092, 15-07-01174, 15-37-20723 и 15-47-02492.