Пучки только с поперечной интенсивностью в фокусе

В настоящее время отмечается рост интереса исследователей к использованию азимутально-поляризованного света [1]. Первоначально азимутальная поляризация предлагалась для получения компактных пятен [2, 3]. Однако позднее были найдены и другие ее применения. Например, в работах [4, 5] азимутально-поляризованный пучок используется для генерации третьей гармоники в ансамблях кремниевых наночастиц (квадрумеров и тримеров). Именно азимутально-поляризованный свет оказался наиболее подходящим для возбуждения Ми резонансов в исследуемых олигомерах – было достигнуто улучшение генерации на два порядка по сравнению с использованием линейной поляризации. В работе [6] предложен оптоволоконный сенсор, в котором в качестве основной моды распространяется азимутально-поляризованная мода.

Достаточно интригующим видится использование азимутально-поляризованного света для манипуляций с намагниченностью, последняя вычисляется как векторное произведение напряженности электрического поля на ее комплексное сопряжение: M ~ E × E*. В первую очередь повышенный интерес к изучению намагниченности вызван её возможным применением в системах оптомагнитной памяти [7, 8]. Из-за отсутствия продольной составляющей электрического поля намагниченность в азимутально-поляризованном пучке всегда направлена вдоль оси распространения. Таким образом ранее удавалось получать пятна [9], иглы [10, 11], цепочки [12, 13] и массивы [14] намагниченности. В работе [15] наблюдается усиление магнитного поля в центре квадруполей и гексаполей из кремниевых микросфер при освещении их светом азимутальной поляризации.

Отметим, что в классическом азимутально-поляризованном пучке направление поляризации меняется непрерывно [1]. В данной работе будет показано, что такие же свойства, как у азимутально-поляризованных пучков, могут быть получены и у секторных азимутально-поляризованных пучков, содержащих V-линии сингулярности. Ранее подобные кусочно-непрерывные состояния поляризаций рассматривались в работах [16– 18]. В работе [16] рассматривались оптические вихри с цилиндрической поляризацией полуцелых порядков. В работе [17] рассматривалась фокусировка векторных пучков дробных порядков, а в работе [18] – векторный пучок, «сшиваемый» из двух других векторных пучков – верхняя половина с одним порядком, нижняя – с другим. Изначально в таких пучках отсутствует спин: поляризация в каждой точке фокусируемого пучка является линейной, однако при острой фокусировке возникает ненулевая продольная составляющая спинового углового момента, что говорит о появлении областей, в которых поляризация эллиптична. Данный эффект является частным случаем спин-орбитального взаимодействия в остром фокусе. Создавать пучки с разрывами поляризации можно с помощью метаповерхностей: на основе суперосцилляций [19] или субволновых решеток [20].

В данной работе численно с помощью формул Ричардса–Вольфа была промоделирована острая фокусировка векторных пучков с азимутальной поляризацией и пучков с V-линией неопределённости поляризации. Было продемонстрировано, что в остром фокусе для этих пучков отсутствует продольная составляющая напряженности электрического поля. Ранее подобный эффект демонстрировался только для азимутально-поляризованных пучков. Отсутствие продольной составляющей напряженности электрического поля приводит к отсутствию поперечных составляющих спинового углового момента и поперечных составляющих намагниченности. Была показана возможность создания секторных азимутально-поляризованных пучков с помощью векторных волновых пластинок.

1. Моделирование острой фокусировки Формулы Ричардса–Вольфа

Моделирование в данной работе было проведено через вычисление в среде Matlab интеграла Ричардса– Вольфа [21, 22]:

• г а 2п

E ( р , у , z ) = - if J J B ( 0 , ф ) Т ( 0 ) P ( 0 , ф ) х

^ 0 0

х exp { ik [р sin 0 cos ( ф-у ) + z cos 0^| } sin 0 d 0 d ф ,

где E (ρ, ψ, z ) – напряжённость электрического поля в фокусе, B (θ, φ) – амплитуда электрического поля во входном зрачке широкоапертурной оптической системы (θ – полярный угол, φ – азимутальный), T (θ) – функция аподизации линзы, f – фокусное расстояние, k =2π /λ – волновое число, λ – длина волны (в моделировании считалась равной 532 нм), α – максимальный полярный угол, определяемый числовой апертурой линзы ( NA =sin α), P (θ, φ) – вектор поляризации для напряжённости электрического поля, имеющий вид:

P ( 0 , ф ) =

1 + cos ² ф ( cos 0- 1 ) sin ф cos ф ( cos 0- 1 ) - sin 0 cos ф

sin ф cos ф ( cos 0- 1 ) 1 + sin ² ф ( cos 0- 1 ) - sin 0 sin ф

a ( 0 , ф ) +

b ( 0 , ф ) ,

где a (θ, φ) и b (θ, φ) – функции, описывающие состояние поляризации x - и y -компонент напряжённостей фокусируемых пучков. Для простоты вычислений в моделировании считалось, что зонная пластинка ( T (θ) = cos (θ)^–3/2 [23], NA = 0,95) фокусирует плоскую волну B (θ, φ)= 1 в воздухе n = 1.

Азимутально-поляризованный свет

Поляризация, при которой напряженность электрического поля направлена строго азимутально, известна уже достаточно хорошо. Отсутствие в данном случае продольной составляющей напряженности электрического поля следует непосредственно из век-

торных уравнений Максвелла, записанных для цилиндрической системы координат: при обнулении производной по азимутальному углу система из шести уравнений разбивается на две системы, каждая из которых содержит по три уравнения (можно провести аналогию с ТЕ- и ТМ-поляризацией). Одна из систем тогда имеет вид:

d H p д z

дндEv _, др 0 dt Ev,

<

д E у = д z

-I

д H р

■ ,ЩЬ „ , д t

1 д ( р e у )        д H z

—-—- ^^- , , д t

_р др

где Н – напряженность магнитного поля, ε и μ – диэлектрическая и магнитная проницаемости, ε 0 и μ 0 – электрическая и магнитная постоянные. Поле, описываемое (3), содержит только одну компоненту электрической напряженности.

Для классического азимутального пучка напряженность электрической компоненты исходного пучка в (1) имеет вид:

E ( 0 , ф )

f a (^фГ | t b ⁽ф⁾J

- sin ф cos ф

Подставив уравнение (4) в (2), можно видеть, что

P _z ( 0 , ф ) = sin 0 cos ф sin ф- sin 0 sin ф cos ф = 0. (5)

Ранее изучался только случай азимутальной поляризации. Азимутальная поляризация – частный случай пучка с V-точкой сингулярности [24], расположенной в центре пучка. На рис. 1 показано направление поляризации в исследуемых пучках: на рис. 1 а показано направление для азимутально-поляризованного пучка. Отметим, что направление поляризации в пучке на рис. 1 б совпадает с направлением поляризации азимутально-поляризованного пучка, прошедшего через бинарную ступеньку [25, 26].

Результат фокусировки азимутально-поляризованного пучка показан на рис. 2. Показано распределение интенсивности (рис. 2 а ) и ее отдельных составляющих. Из рис. 2 г видно, что продольная составляющая равна нулю.

Отметим, что отсутствие продольной составляющей напряженности электрического поля приводит к тому, что вектор спинового углового момента будет содержать только продольную компоненту:

S = 8-1 - Im ( E * х E ) , (6)

где ω – угловая частота света. Постоянную 1/(8πω) будем опускать. Интересно, что спиновый угловой момент противоположен, а по абсолютному значению отличается лишь множителем от вектора намагниченности:

M = i γ [ E × E *],

где γ – магнитооптическая восприимчивость.

(а)

(в)

t i M^^v UMM И И ПЛ м и t И

.^x/// /

(г)

И И ИЛ ЛИ И И

(б)

V/xx*--^*-'	^^xXK X
У /XXX^	Лхх\\X
У j(/K^^*"	^xxxV\X
v //xx-*^	.xXW h \
V///xx*.	kX W \ И
MM >x И H M"^	x M H M
* 1 HW	mww
A X \xx^'	'^ * # i i t
	* * ^ У V V
	-»"X >■ ^ # f
.X X хж^-».^^	X к ^ ^
	^^.^///Ук

И / М /л М И И

В (9) x = kr sin9, J m ( x ) - функция Бесселя m -го порядка, A (θ) – действительная функция, описывающая амплитуду входного поля в плоскости входного зрачка апланатической системы, зависящая только от угла θ . Подставив (8) в (6), можно показать, что продольная компонента СУМ всегда будет нулевой.

Пучок с V-линией неопределенности поляризации – секторная азимутальная поляризация

Можно получать и другие пучки, не обладающие z -компонентой электрического поля. Такое возможно, если в пучке, помимо V-точки сингулярности в центре, будут также V-линии сингулярностей [24]. В таком случае для начального поля (1) функции поляризации будут иметь вид [28]:

E ( 9 , ф ) =

^f a Ml t b wj

cos(2 ф ) - 1 sin(2 ф )

Подставив (10) в (2), можно показать, что:

Рис. 1. Направление поляризации в исследуемых пучках: азимутально-поляризованном (а), пучке с V-линией сингулярности (б, в), пучке с двумя V-линиями сингулярности (г)

P z ( 9 , ф ) =

= - sin 9 cos ф ( cos ( 2 ф ) - 1 ) - sin 9 sin ф sin ( 2 ф ) =     (11)

- sin 9< - cos ф + cos ф cos ( 2 ф ) + sin ф sin ( 2 ф ) [ = 0.

cosф

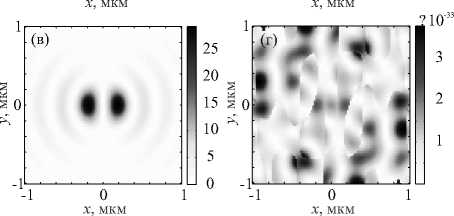
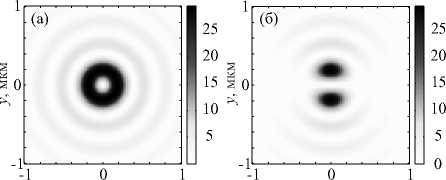
Рис. 2. Двумерные распределения интенсивности и её отдельных составляющих в фокусе пучка с азимутальной поляризацией первого порядка: I (а), Ix (б), Iy (в), Iz (г)

На рис. 3 показано распределение интенсивности и ее отдельных составляющих в плоскости фокуса для пучка (8). А на рис. 4 – распределение продольной составляющей СУМ на расстоянии λ от фокуса: непосредственно в фокусе для этого пучка все компоненты СУМ равны нулю [28]. Под интенсивностью понимается сумма квадратов модулей отдельных компонент напряженности электрического поля: I =| E x |²+| E y |²+| E z |²= I x + I y + I z [1].

Ранее [27] было показано, что компоненты напряженности электрического поля для азимутально-поляризованного света имеют вид:

E x = - sin ф [ 1 1 - 1 2 ] ,

E y = cos ф [ 1 1 - 1 2 ] ,                                 (8)

E z = 0,

где

I = — [sin 9 cos ¹/² 9 (1 + cos 9 ) A ( 9 )e ik ^{cos 6} Ji ( x ) d 9 , ^ 0

I ₂ = f [sin 9 cos ¹/² 9 (1 - cos 9 ) A ( 9 )e ^ikzcos ⁹ J_ ]( x ) d 9 . ^ 0

s

s

-1-1

-1-1

x, мкм x, мкм

Рис. 3. Двумерные распределения интенсивности и её отдельных составляющих в фокусе пучка с V-линией неопределённости поляризации: I = Ix + Iy + Iz (а), Ix (б), Iy (в), Iz (г)

0,5

-0,5

-1

-1 -0,5 0 0,5 1

0,5

-0,5

-1

x, мкм

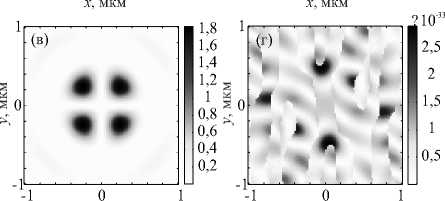
Рис. 4. Распределение продольной компоненты спинового углового момента Sz на расстоянии λ от фокуса

Аналогичный пучок с V-линией неопределенности сингулярности, но повернутый относительно пучка (8), имеет вид (рис. 1 в ):

а ( ф ) = sin ( 2 ф ) , b ( ф ) = - cos ( 2 ф ) - 1.

Можно также посекторно задавать направление поляризации. Например, 1-й и 3-й секторы - ( а ( ф )=-sin( ф ), b ( ф ) = cos( ф )), а 2-й и 4-й - ( а ( ф ) = sin( ф ), b ( ф ) = -cos ( ф )). Такое векторное поле будет обладать двумя V-линиями неопределенности поляризации (рис. 1 г ). Для данного случая результат фокусировки приведен на рис. 5–6. На рис. 5 показана интенсивность и ее составляющие, а на рис. 6 – продольная компонента СУМ в фокусе.

-1-1

2 'Z

x , мкм

-1

'z

x , мкм

Рис. 5. Двумерные распределения интенсивности и её отдельных составляющих в фокусе пучка с двумя V-линиями неопределённости поляризации: I (а), Ix (б), Iy (в), Iz (г)

-1

2.    Экспериментальное получение пучков

Для получения азимутально-поляризованного света в настоящее время есть коммерчески доступные q-пластинки (нами использовался LBTEK VR1). Падающий на такой элемент линейно-поляризованный вдоль оси x свет преобразуется в азимутально-поляризованный пучок, а линейно-поляризованный вдоль оси y – в радиально-поляризованный пучок, реализуя таким образом матрицу Джонса:

-1

-2

-3

• x, мкм

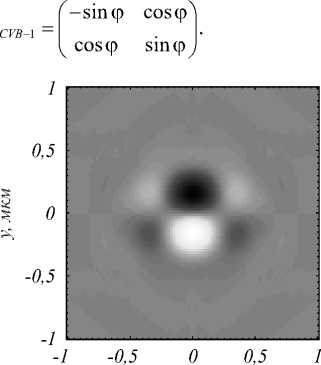
Рис. 6. Распределение продольной компоненты спинового углового момента Sz в фокусе

На рис. 7 показана интенсивность пучка, полученного при прохождении линейно-поляризованного света через q -пластинку при разных положениях поляризатора-анализатора перед регистрирующей камерой. Отметим здесь, что регистрация поперечных компонент не представляет труда, в то время как регистрация продольной компоненты невозможна прямыми измерениями. Однако продольная компонента может быть вычислена через измеренные поперечные компоненты. Например, в [29] продольная компонента вычислялась с помощью Стокс-полариметрии и итерационного алгоритма восстановления фазы.

Рис. 7. Изображение азимутально-поляризованного пучка на камере без анализатора (а) и с анализатором, повернутым на угол 0 (б) и 90 градусов (в)

Из рис. 7 видно, что поляризация пучка соответствует азимутальной.

Получить пучки (10) можно также с помощью q-пластинки. Для этого можно пропустить через элемент (13) линейно-поляризованный вдоль оси x пу- чок, но такой, в котором поляризация нижнего сегмента отличается знаком от верхнего сегмента. Тогда поляризация для верхнего сегмента пучка будет описываться вектором Джонса:

• -    sin ф cos ф 1 - sin ф

E =1 .  -*1Ш    J I ,         (14)

^ cosф SinфJ^0J ^cosф J а для нижнего:

• -    sin ф cos ф - 1 sin ф

E = I II I = I | .                  (15)

^ cos ф sin фJ^ 0 J ^- cos фJ

В качестве пучка, в котором поляризация отдельных сегментов отличается знаком, можно взять пучок Гаусса–Эрмита (0,1). Нами для получения пучка Гаусса–Эрмита использовался пропускающий модулятор Holoeye LC2012 (рис. 8). Затем пучок совмещался с центром q -пластинки. Получившийся пучок фокусировался линзой L 4 с малой числовой апертурой на камеру, перед которой помещался поляризатор-анализатор P 3 . Результат фокусировки показан на рис. 9.

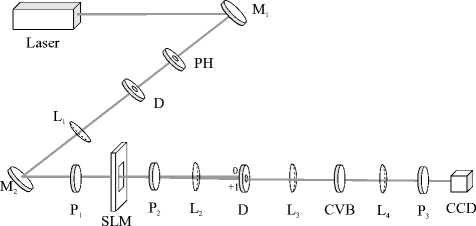
Рис. 8. Laser – лазер MGL-F-532-700 (λ = 532 нм), M1, M2, – зеркала, PH – пинхол (диаметр отверстия – 50 мкм), L1 – L4 – линзы (f1 = 400 мм, f2 = 150 мм, f3 = 125 мм, f4 = 100 мм), D – ирисовая диафрагма, SLM – пространственный модулятор света (Holoeye LC 2012), P1-P3 – поляризаторы, CVB – векторная волновая пластинка (LBTEK VR1), CCD –

CCD-камера (UCMOS10000KPA)

Рис. 9. Изображение сфокусированного пучка с V-линией неопределенности поляризации (10) на камере без анализатора (а) и с анализатором, повернутым на угол 0 (б) и 90 градусов (в)

Из рис. 9 видно, что, несмотря на малую числовую апертуру фокусирующей линзы, картина распределения интенсивности в фокусе согласуется с моделированием (рис. 3).

Заключение

В данной работе численно с помощью формул Ричардса–Вольфа была промоделирована острая фокусировка векторных пучков с азимутальной поляризацией и пучков с V-линией неопределённости поляризации. Было продемонстрировано, что в остром фокусе для этих пучков отсутствует продольная составляющая напряженности электрического поля. Ранее подобный эффект демонстрировался только для азимутально-поляризованных пучков. Наличие V-линий и отсутствие продольной компоненты напряженности электрического поля приводит к тому, что вектор спинового углового момента содержит только продольную компоненту. Была также показана возможность экспериментальной генерации исследуемых пучков.

Работа выполнена при поддержке гранта Российского научного фонда № 23-12-00236 (в части теории) и в рамках Государственного задания НИЦ «Курчатовский институт» (в части эксперимента).