Пыльный вихрь и волчок

Широко известен пыльный вихрь, который представляет собой почти вертикальный столб пыли – см. рис. 1. Такой вихрь имеет вертикальную ось вращения, высоту - несколько десятков метров, диаметр – несколько метров, скорость внутри вихря – около 10 м/сек, время существования - несколько десятков секунд [8]. Существуют и подобные ему явления –воздушный, пепловый, водяной вихри – см. рис. 2 из [9]. Этот вихрь имеет диаметр около 0.1 м. Причинами возникновения песчаных вихрей принято считать различные атмосферные явления (ветер, нагрев атмосферы). Однако само существование песчаного вихря - сохранение формы и движение трудно объяснить теми же причинами. Кроме того, существуют и движутся такие вихри и на Марсе, где атмосфера отсутствует [8]. Поэтому при объяснении таких вихрей главными являются вопросы об источнике энергии и причинах устойчивости в столь необычной форме.

Автор уже рассматривал в [4] математическую пыльного вихря. В отличие от этого ниже предлагаемая модель, где явным образом используются силы Кориолиса (реальность которых обоснована в [1, 2]), как внутренние силы, обеспечивающие устойчивость вертикальной струи. Возможно, что обе эти модели удастся объединить, но здесь не делается таких попыток и не выполняется какое-либо сопоставление прежней и новой моделей.

Рис. 1.

Рис. 2.

Далее рассматривается вопрос: «Как устроен пыльный вихрь?», а вопрос «Как она возникает?» остается без ответа.

2.    Волчок

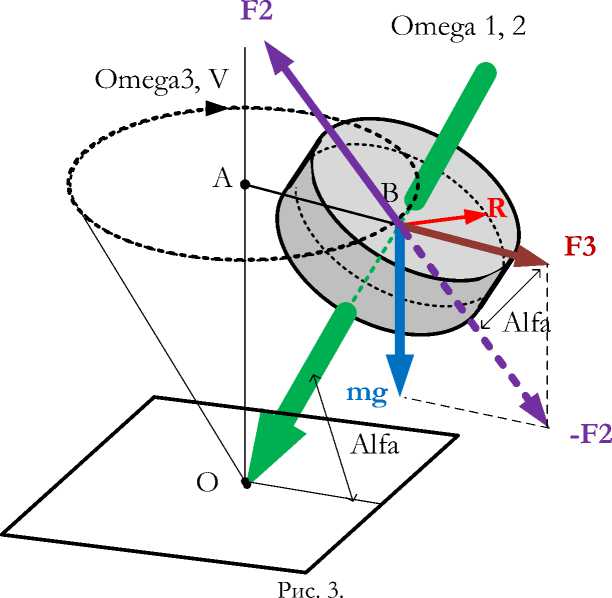
На рис. 3 показан волчок в простейшем варианте. При этом волчок с массой т имеет вид цилиндра с радиусом R и высотой h , наклонен к горизонтальной плоскости под углом К . У волчка существуют

• •    вращение волчка вокруг собственной вертикальной оси с угловой скоростью W_{1 ?}

• •    вращение волчка, наклоненного под углом К к горизонтальной плоскости, вокруг собственной оси с угловой скоростью w₂,

• •    прецессия по окружности волчка, наклоненного под углом К к плоскости, с угловой скоростью w₃ ,

• ♦    линейная скорость прецессии V ; это скорость движения т.

В на радиусе АВ, вращающемся с угловой скоростью ^ 3 (см. рис. 3):

v = M₃hcos(&y                               (1)

В [3] показано, что
1 ш3 = nR2- -----777^-1. 5         (q+nR2/^ 1	(2)
(b-a)	(3)
Ш7 =     7^1 , 2    (a+b)  1 ,
где
q = h 2 — (^h 2 — R2^ &. ,	(4)
a = 4nR 2 ,	(5)
b = n 2 R 4 /q.	(6)

В [3] построена математическая модель волчка в которой приняты следующие обозначения действующих сил и механических моментов (см. рис. 3):

• •    сила Кориолиса, действующая на т. В на радиусе АВ,

F2 = -2тш2 x v;(7)

• •    центробежная сила, направленная по горизонтали АВ от центра,

F3 = m^2^cos(^);

• •    сила тяжести, направленная вертикально вниз,

F^ = —mg;(9)

• •    суммарная сила, как векторная сумма,

Fs = F2+F3+F4;(10)

• •    горизонтальная и вертикальная проекции этой силы F_sx и F_sy соответственно;

• •    опрокидывающий момент вращения волчка вокруг точки вращения

М = hF_sxsin(x) — hF_sycos(x).                  (11)

• •    cила давления на точку вращения, направленную вдоль штанги,

Т = —hF_sxcos(x) — hF_sysin(x).                 (12)

Построенная таким образом математическая модель волчка позволяет ответить на вопрос о том, почему волчок не падает. Этот вопрос не нов. Его задавал в 1890 г. проф. Джон Перри [10, стр. 93]. Он писал «…в волчке, очевидно, только с вращением появляется жизнь и устойчивость, или, другими словами, только тогда выступают силы, противодействующие земному притяжению, которое стремится опрокинуть волчок. Откуда берутся эти силы и чем они объясняются?» Вопрошающий интуитивно чувствует, что первоначальный толчок не может дать ту 118

энергию, которая нужна для долгого и энергичного вращения. Ответ полученный в [3] состоит в том, что в волчке действуют реальные (не фиктивные) силы Кориолиса и центробежных силы.

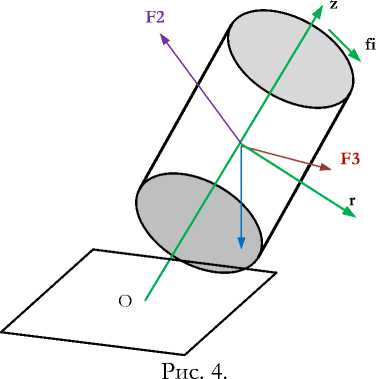
Перечисленные выше силы, очевидно, действуют на каждую точку – элементарную массу волчка. Рассмотрим такие массовые силы в цилиндрической системе координат г, ф, z , где ось z совпадает с осью цилиндра, т.е. наклонена под углом К к горизонтальной плоскости -см. рис. 4. Бyдем обозначать такие массовые силы как F_r, F y , F_z. Для вычисления этих сил заметим предварительно, что вместо сил F₂, F₃, F₄ необходимо использовать соответственно силы

А = ^—- F, f₃ = ^r F  f = - F₄ .           (13)

J 2   mR 2   3 mR 3   4 m 4               v 7

Здесь коэффициент — появляется потому, что все силы, отнесенные ко всей массе волчка, должны относиться к единице массы р — удельной массе материала. Коэффициент - появляется потому, что

R силы F2,F3, рассчитываемые относительно радиуса волчка, должны рассчитываться относительно радиуса г текущей точки. Обозначим векторную сумму:

fs=f2+f3+f4.(14)

Обозначим еще проекции этой силы на ось z и на ось г , как f_sz и f_sr соответственно. Тогда получим :

Fr = fsr,(15)

Fp = 0,(16)

Fz = fsz.(17)

Предположим теперь, что материалом волчка является жидкость, но он тем не менее сохраняет свою цилиндрическую форму . В таком жидком волчке должны соблюдаться законы гидродинамики, т.е. возникшие в нем массовые силы F_r, F ^ , F_z должны вызвать внутренние течения – массовые тока жидкости со скоростями V_r, V ^ ,V_z. Можно полагать, что эти внутренние течения не меняют распределение масс внутри волчка и поэтому не изменяют массовые силы и скорости волчка, как целого. Однако массовые силы F r ,F p ,F z должны будут выполнять работу на преодоление внутреннего трения, т.е. время существования такого волчка будет ограничено.

3. Уравнения гидродинамики

Очевидно, для описания жидкого волчка следует использовать гидродинамику. Уравнения гидродинамики для вязкой несжимаемой жидкости имеют следующий вид [6]:

div(v) = 0 ,                                        (18)

Р^ + Vp — pДv + p(v ■ V)v — pF = 0 ,         (19)

где p = const - постоянная плотность, p - коэффициент внутреннего трения,

• p - неизвестное давление,

• и = \у_х> V y , V z ] - неизвестная скорость, вектор,

F = [F_x,F_y,Fz] - известная массовая сила, вектор,

• X, y,z,t - пространственные координаты и время.

В этих уравнениях неизвестны p, V .

Если система является замкнутой, то система уравнений (18, 19) в стационарном режиме принимает вид [6]:

div(v) = 0,                                         (20)

• —p^v + VD—p^F = 0,                  (21)

где неизвестны D.V . Уравнение (21) решается методом, предложенным [6]. При этом решение всегда существует и является единственным. После решения уравнения (21) определяются скорости и величина D , а давление вычисляется по уравнению вида

P = ~(W ² ) ,                                (22)

где

W ² = (У * + V y + v_z).

В (22) слева – давление, а справа плотность кинетической энергии течения . Интеграл плотности по объему определяет энергию в объеме водоворота

Если система абсолютно замкнута (например, в безбрежном океане или просто при достаточно большом максимальном радиусе), то выполняется условие ^D ~ 0. Таким образом, для замкнутой системы выполняются уравнение вида р ■ Av + р ■ F = 0.                                  (24)

и определяется плотность энергии (22). Метод расчета таков, что не требует знания граничных условий – точность расчета тем больше, чем больше область интегрирования

Будем рассматривать математическую модель жидкого волчка в системе цилиндрических координат Г, ф, Z. Предположим, что в нем существуют скорости, направленные вдоль этих осей vr, v^, vz и являющиеся функциями этих координат.

В уравнении (24) с учетом (15-17) принимает вид р- Avr + fsr = 0, р- Av^ = 0,

Р ■ Avz+ fsZ = 0, где лагранжиан Av в цилиндрических координатах определяется

формулой вида Г |( ^ + г)Э A v=kl-е+г)£ LAVz -1     /1 л аЛг 1ч+г)—

1 d2vr d2vr " r2 дф2 dz2 + 4тЭ + Т^'     (28) r2 дф2    dz2 + 1 d2vz + d2vz r2 дф2 dz2 -

Из (26, 28) следует, что

д2*Ф - n д*Ф - г dr2    0, dr C, Vф   СГ, (29) где С - некоторая константа. По определению, Vф = ыг,                                        (30) следовательно, формула (26) соответствует формуле (30). При этом система уравнений (25-27) вырождается в систему двух уравнений: (1 । ..V2vr , 1 d2vr , d2vr , r z      n \r ' Ч dr2 ' r2 дф2 ' dz2 ' Jsr/ р А тЛ^г V + Г) dr2 + r2 дф2 + dz2 + fsz/P Решение этой системы уравнений имеет вид: vr = br(r) • exp(<* ф + xz) Vz = bz(r) • exp(« ф + xz), , 0. () (32) (33) (34) где ^,Х - некоторые константы, а b(r) — неизвестные функции аргумента г. Тогда уравнения (31, 38) после сокращения на общие множители примут вид:

( г ^{+ г}) 1^ ⁺ ^^{Ьг +} ^ + ^f r ^/p = °'

Q ^{+ r})^ ⁺ ^^b z +X^2b z ⁺f sz^ = °.        (³⁶⁾

При вышеопределенных функциях f_sr(v) и f_sz(r') эти уравнения могут быть решены численным дифференцированием.

Давление внутри цилиндра может быть найдено (22, 23):

Р = -2^Vr +^ф + ^Я

Это давление превращает жидкий цилиндр волчка в твердое тело и удерживает жидкость в объеме цилиндра. Поэтому жидкий цилиндр ведет себя твердый волчок. Распространение этого утверждения на «пыльный цилиндр» требует более строгих доказательств. Но мы пока удовлетворимся ссылкой на эксперименты, поставленные природой: водный и пыльный вихри идентичны – см. рис. 1 и рис. 2. Другая аналогия следует из [11]: струя воды ведет себя как твердое сверло, при добавлении в воду абразива это сверло становится еще тверже.