Quantum fuzzy inference gate design in robust intelligent control of robotics and mechatronics

Soft computing methodologies, such as genetic algorithms (GA) and fuzzy neural networks (FNN) had expanded application areas of fuzzy controller (FC) by adding optimization, learning and adaptation features [1, 2]. For complex and ill-defined (fuzzy) dynamic control objects that are not easily controlled by conventional control systems (such as proportional-integral-derivative – PID-controllers) – especially in the presence of fuzzy model parameters and different stochastic noises – the System of Systems Engineering methodology provides fuzzy controllers (FC) as one of alternative way of control systems design [3].

It is difficult to design optimal and robust intelligent control system, when its operational conditions have to evolve dramatically (aging, sensor failure and so on). Such conditions can be predicted but it is difficult to cover such situations by a single knowledge base (KB) of FC.

Using unconventional computational intelligence toolkit we propose a solution of such kind of generalization problems by introducing a self-organization design process of robust KB-FC that supported by the Quantum Fuzzy Inference (QFI) based on quantum soft computing ideas [4 – 7].

Problem’s Formulation

• A.    Main problem and tools

The learning and adaptation problems of FC’s are the interesting topic in control theory. Many existing solutions are using different models of artificial neural networks based on the back-propagation (BP) algorithm, Kohoen multilayer structure and so on [1]. Adaptation processes have based on different models of iterative stochastic algorithms. These schemes are successfully working if the control task performed in absence of underdetermined stochastic noises in world environments, in sensors, in control loop, etc.

Unfortunately, methods based on BP-algorithms and iterative stochastic algorithms do not guarantee the required control robustness level and accuracy in complex unpredicted control situations.

One of main problem in modern FC design technology is how to design and introduce robust KBs into control system for increasing self-learning, self-adaptation and self-organizing capabilities that enhance robustness of developed FC in unpredicted control situations [5].

The solution of this task based on Soft Computing Optimizer (SCO) is developed in [2]. QFI model including allows self-organization level in intelligent control system [3 – 7]. QFI uses the laws of quantum computing technologies [8 – 10] and applies next operations: superposition, quantum correlations (entanglement or quantum oracle), and interference [9 – 11].

• B.    Method of solution

Proposed QFI system consists of a few FCs, each of which provides solution in one set conditions of control system [2]. QFI system revises the results of fuzzy inference of each independent FC and proposes in on-line the generalized control signal output [5]. The output QFI signal combines best features of the each independent FCs.

• C.    Main goal

The main purpose of QFI is to produce a self-organization capability for many unpredicted control situations. QFI produces robust optimal control signal for the actual control situation using a redundant amount of information in KB’s of individual FCs [7, 12].

In this work the main ideas of quantum computation and quantum information theory [9, 10, 13] applied in developed QFI methods are introduced. Robustness of new types of self-organized intelligent control systems is demonstrated.

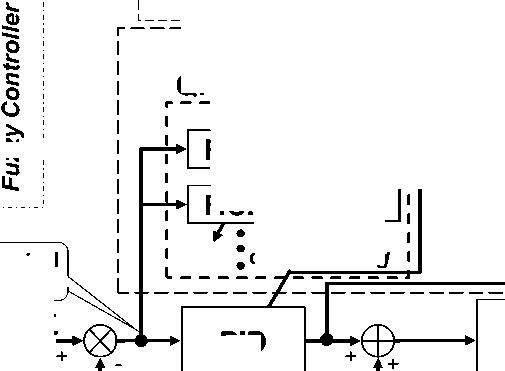
Structure of QFI

QFI design is needed to apply the additional operations as superposition, entanglement (quantum correlation or quantum oracle) and interference that physically are operators of quantum computing.

Let us introduce briefly the particularities of quantum computing and quantum information theory that are used in the quantum block QFI (Fig. 1) supporting a self-organization capability of FC in robust intelligent control system (ICS).

• A.    Quantum computing

The fundamental result of quantum computation stays that all of the computation can be embedded in a circuit, which nodes are the universal gates [9 – 11]. These gates offer an expansion of unitary operator U that evolves the system in order to perform some computation.

Thus, naturally two problems are discussed: (i) Given a set of functional points S = {( x, y )} find the operator U such that y = U • x ; (ii) Given a problem, fined the quantum circuit that solves it.

E

Design of robust KB on-line tuning off-line tuning QFC

О co 3 О

SCO + QCO

Ref.

PID

Control error

N N

F.C. 1

QFI

F.C. 2

Noise in model parameters

Delay time in sensor

m(t)

Z-1

Noise with timedependent statistics

Control object

Real physical object or simulation model

Noise in sensor

Control Situation

New more realistic control situations

Figure 1. Structure of robust ICS based on QFI model

Algorithms for solving problems of quantum computing may be implemented in a hardware quantum gate or in software as computer programs running on a classical computer. It shows that in quantum computing the construction of a universal quantum simulator based on classical effective simulation is possible in [10, 11].

In the general form, the model of quantum algorithm computing comprises the following stages:

• -    preparation of the initial state | ^ _out );

• -    application the Hadamard transform for the initial state in order to prepare the superposition state;

• -    application of the quantum correlation operator to the designed superposition state;

• -    application of the interference operator;

• -   application of the measurement operator to the result of quantum computing | ^ _out ).

Hence, a quantum gate approach can be used in a global optimization of KB structures of ICSs that are based on quantum computing, on a quantum genetic search and quantum learning algorithms [3, 11].

• B.    Quantum information resources in QFI algorithm

The quantum algorithm for QFI the following actions are realized [3, 14, 16]:

• -    The results of fuzzy inference are processed for each independent FC;

• -    Based on the methods of quantum information theory, valuable quantum information amount hidden in independent (individual) KBs is extracted;

• -    In on-line, the generalized output robust control signal is designed in all sets of KBs of the FC.

• -    The output signal of QFI in on-line is an optimal signal of control of the PID controller gains schedule.

2.Entanglement (Oracle)

Therefore, the domain of efficiency of the ICS can be extended by including robustness property, which is a very important characteristic of control quality [2, 3].

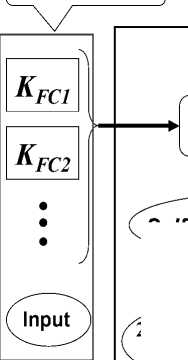
QFI use unitary invertible (quantum) operators (Fig. 2) for computing physical laws of control. They based on of quantum information theory as following: superposition, quantum correlation (entangled operators), and interference. The forth operator, measurement of result quantum computation, is classical and irreversible.

max. for normalization probability density function

SC Optimizer

T emplating

max K

normalization

I

Self-Organization

QFI block

P

Choice of Correlation type

quantum state

(Q-bit)  II

4 states selection

2 4 = 16 possibilities

SelfAssembly

1.Superposition

3.Interference

max. probability Amp.

Extraction of hidden quantum information

selected (measured) possibility

[ scaling factor p

IV

III

Grover’s Searching Q-Gate

should be implemented

New_{K QFI}

Decoding

VI

C = { C p , C d , C i }

Result

• Figure 2. The functionality structure of QFI

Optimal control process based on value information amount that extracted from a few KBs (that are designed by soft computing) and are founded on the following facts from quantum information theory [12]: (i) the effective quantum data compression; (ii) the splitting of classical and quantum parts of information in quantum state; (iii) the total correlations in quantum state are “mixture” of classical and quantum correlations; and (iv) the exiting of hidden (locking) classical correlation in quantum state [9, 12, 13].

If these facts are used, the extraction an additional amount of quantum value information from KBs becomes possible to wise control organization. These facts are the informational sources of QFI background. That is QFI using compression and rejection procedures of the redundant information in a classical control signal.

Fig. 2 describes the functional diagram and structure of QFI, and Fig. 3 describes programmable algorithmic gate of QFI realization of which can be implemented using both classical and quantum computer, and can also be integrated into different control system and embedded intelligent controllers.

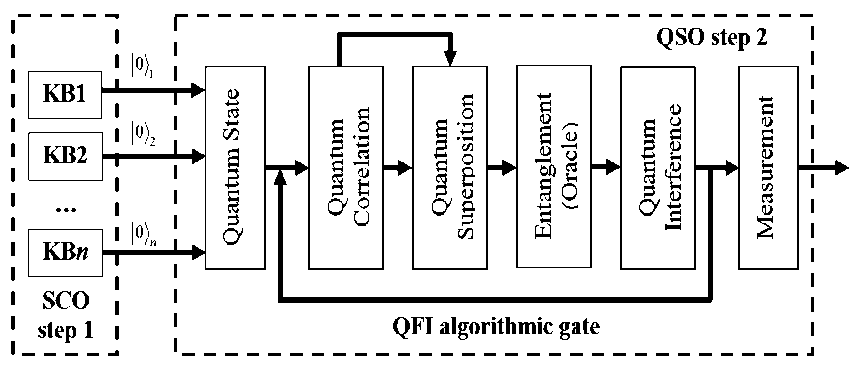
Figure 3. Quantum algorithmic gate of QFI realization

• C.    Remote quantum base optimization

Scaling factor is used in remote quantum base optimization as the adjustable parameter. Scaling factor is used in the final step of forming the gain of PID (Fig. 2).

During operation, data in symbolic form are passed via COM-port. The control system reads data from the sensors and sends them to a computer for further processing. By taking the input values, the GA evaluates the previous decision, and carries a QFI to check the following solutions. The result of the QFI is sent to the remote device for generates of control action.

Benchmark’s simulation

Often, FC designed for a typical situation cannot cope with the tasks of control in unforeseen situation. We demonstrate that by introducing a quantum generalization of strategies in fuzzy inference in on-line from a set of pre-defined FC's can achieve additional robustness for unforeseen situations control. This kind of quantum algorithm is a new quantum algorithm without entanglement. Consider an example of globally unstable control object as “cart – pole” and robotic manipulator.

Benchmark 1: Globally unstable control object simulation

This is a typical Benchmark of control theory, they demonstrating a quality of control system. Task of control is to achieve the stability of inverted pendulum in vertical position. The motion of the dynamic system “cart – pole” is described by the following equations (control object is an essentially nonlinear dissipa-

tive system):

^ u + Е f t ) + az + az — mlO1 sin O ^    • g sin O + cos O ---^--1----3--kO ..                            m + m O =------------------- 7---------"777л ------------2-----,                     (1) ( 4 m cos2 O l - 3    mc + m J u + E ( t ) — axz — a^z + ml ( O2 sin O — O cos O ) z —                                                , mc + m

A mathematical model (1) of the control object presented above contains the following variables: 6 is the pendulum deviation angle (degrees); z is the movement of the cart (m); g is the acceleration of gravity (9.8 m/s²); m_c is the pendulum mass (kg); l is the pendulum half-length (m); £ ( t ) is the stochastic excitation; and u is the control force acting on the cart (N).

Note that the model has underdetermined parameters such as friction in the pendulum shaft and friction surface on the wheel. Verification of the model with these parameters was considered in [15].

Compare the different regulators: classic PID controller, with constant coefficients, fuzzy controllers FC1 and FC2, based on SCO, and QFI controllers based on different types of correlations: Quantum-SpaceTime (Q-ST), Quantum-Time (Q-T), Quantum-Space (Q-S). These QFI controllers are based on FC1 and FC2, and optimized using remote connection.

The mathematical modeling and physical experiments in two situations control:

• -    typical situation (S1), the delay of control is standard - 0.015 sec;

• -    unforeseen situation (S2), the delay of the control error - 0.035 seconds.

The simulation results are shown in Fig. 4 – 6.

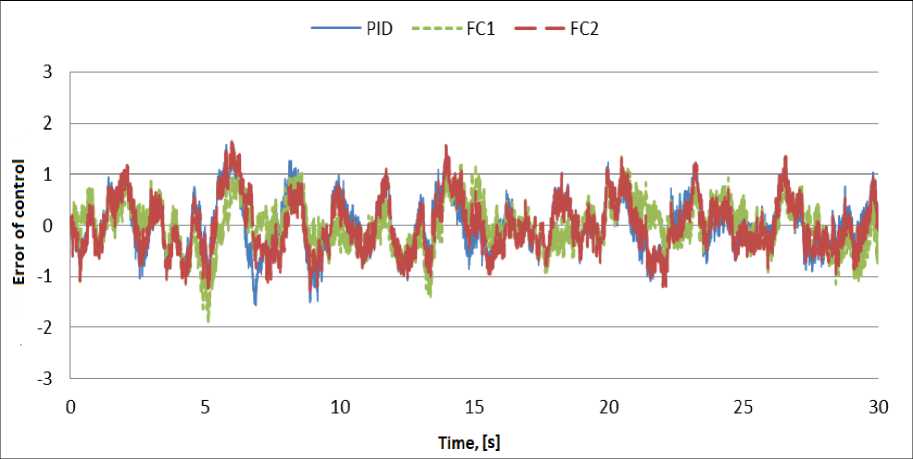
Figure 4. Deflection of pendulum. Simulation in typical situation S1

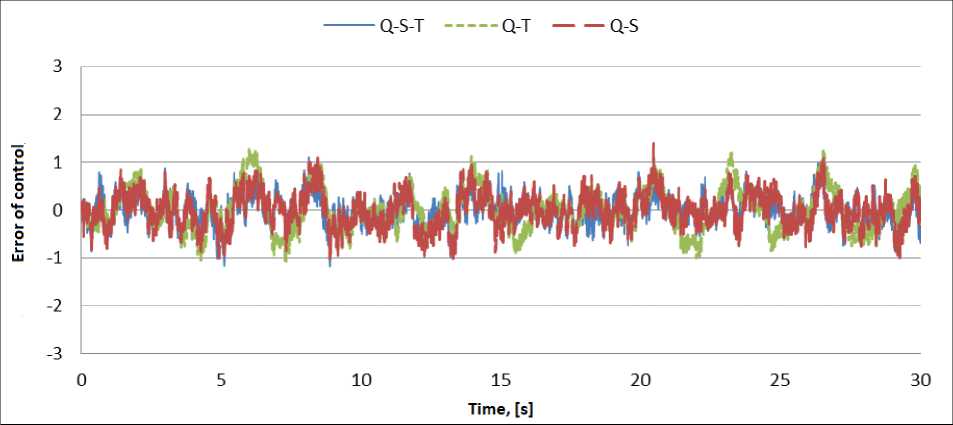
Figure 5. Deflection of pendulum. Simulation in typical situation S1

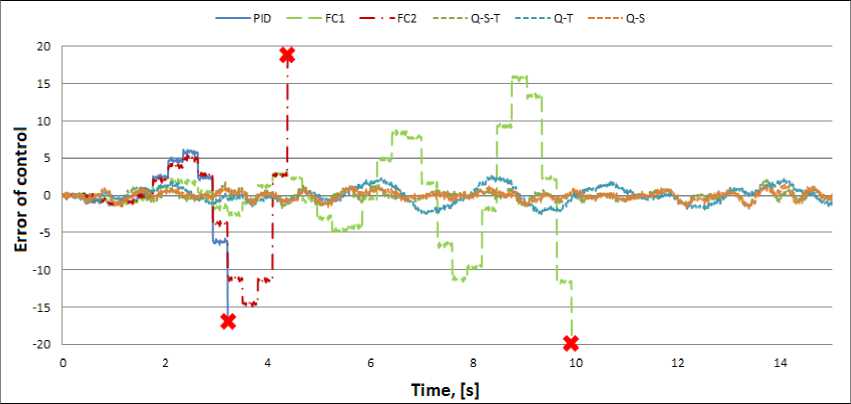
Figure 6. Deflection of pendulum. Simulation in unforeseen situation S2

For experiments, we use a robot that is shown in Fig. 7.

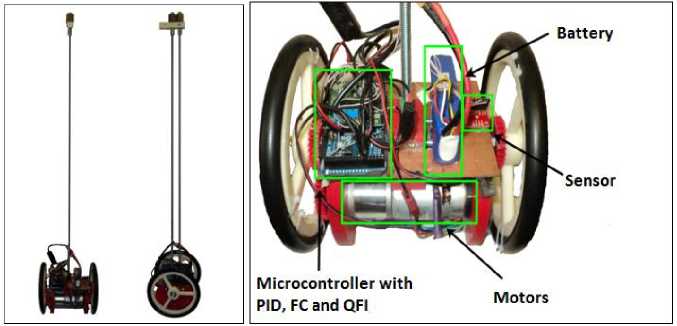
Figure 7. Mobile robot configuration

Result of experiments is shown in Fig. 8 – 10.

As show the results of simulation and experiment, quantum strategy of control can effectively cope with the tasks of control, even in extreme situation in which FC's, underlying QFI, cannot cope with the task of control.

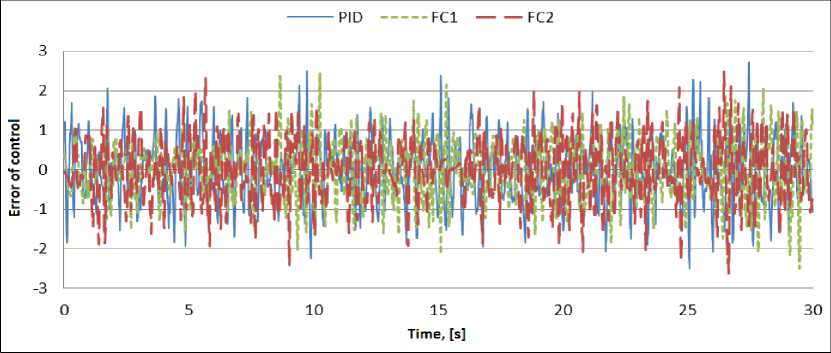
Figure 8. Deflection of pendulum. Experiment in typical situation. PID and FC controllers

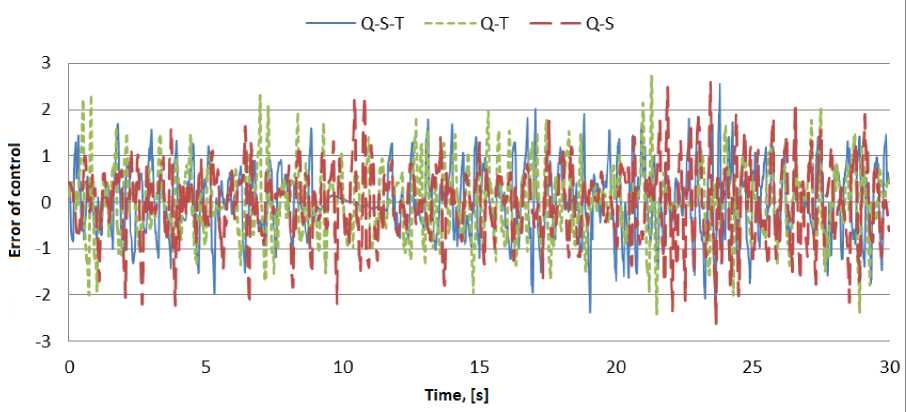
Figure 9. Deflection of pendulum. Experiment in typical situation. QFI controllers

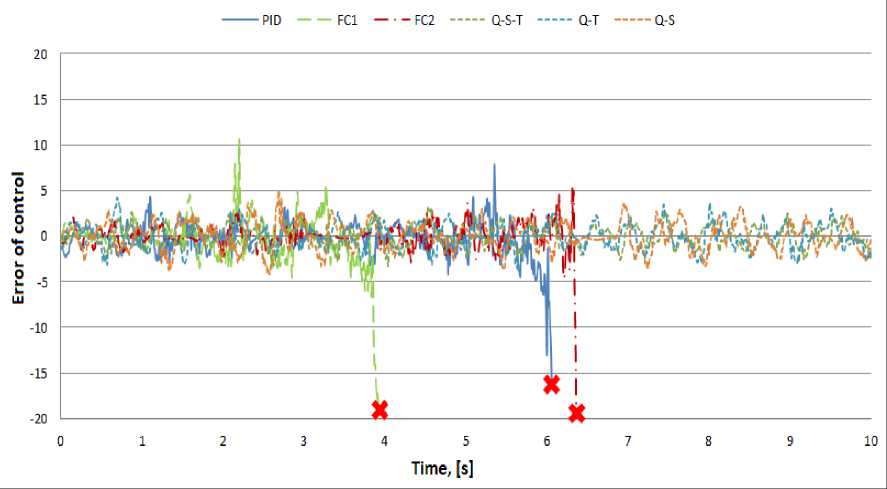
Figure 10. Deflection of pendulum. Experiment in unforeseen situation

Related works Quantum computing approaching in robot path planning, navigation, learning, emotion design, decision making was applied in [19 – 23] etc. Our approach is based on quantum self-organization of knowledge bases using responses of fuzzy controllers on unpredicted situations in online [3, 18].

Benchmark 2: Robotic Manipulator

The seven degrees of freedom (7DoF) and seven-link robotic manipulator is described in this part.

Due control object is complex, ICS for 7DoF manipulator is constructed with using decomposition principal. Seven independent FCs (FC1 – FC7) are used for control each of manipulator link. The decomposition of control allows reducing complexity of constructing ICS.

However, character of ICS somewhat reduced due to independence of seven FCs (Fig. 11).

QFI unit introduction allows improving ICS behavior by self-organization of independent KBs in FC1 – FC7.

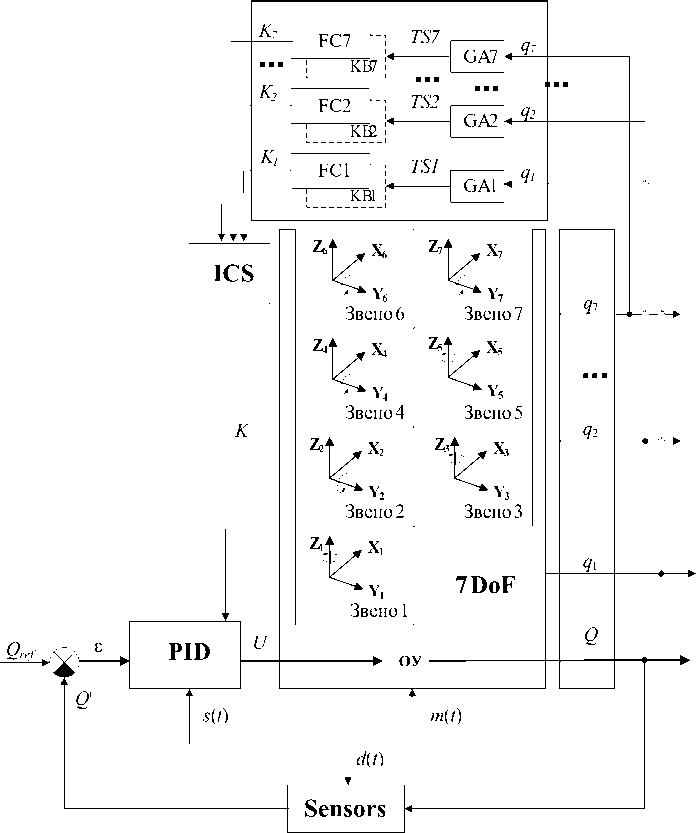
Figure 11. The structure of 7DoF manipulator ICS

Set of performance criteria is entered for estimate of control systems work against accuracy behavior:

• 1.    End Effector Positioning (EEP) error, (m).

• 2.  Relative overshot σ.

• 3.   Relative link positioning error ε.

• 4.   One iteration time t , (s).

• 5.    Complexity of control realization P .

• 6.  Full Control Behavior (FCB):

FCB = wp [EEP] + wp [o] + wp [e] + wP [ t ] + wp, where w = [0.4 0.1 0.1 0.2 0.2] is a weighting coefficient array.

Especially introduction of QFI unit helps to introduce robust control in internal unpredicted situations.

Consider the first internal unpredicted situation – the random noise in the control channel (see, the signal s ( t ) , Fig. 11). Comparison of manipulator behavior for control system based on soft computing and based on quantum soft computing in performance criteria terms is shown in Fig. 12 (on the base results of sixty five experiments).

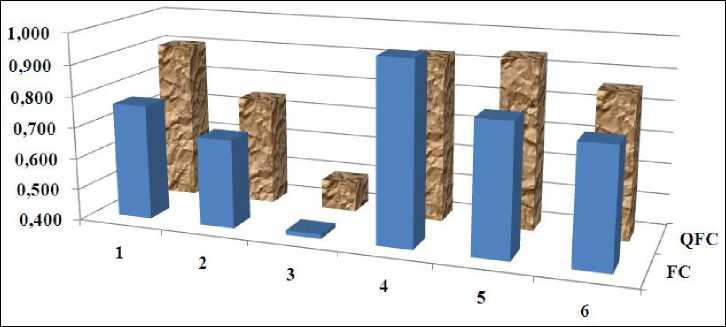
Figure 12. Manipulator behavior with random noise in the control channel: FC – based on soft computing, QFC – based on quantum soft computing

The results are demonstrating if ICS is used with QFI gate, all of evaluation of performance criteria improve (expect “One iteration time”).

The one of cases is shown in Fig. 13. Positioning accuracy is better if used ICS with QFI unit (in this case positioning error is 0.184 m). Positioning error is 1.918 m, if used ICS without QFI unit.

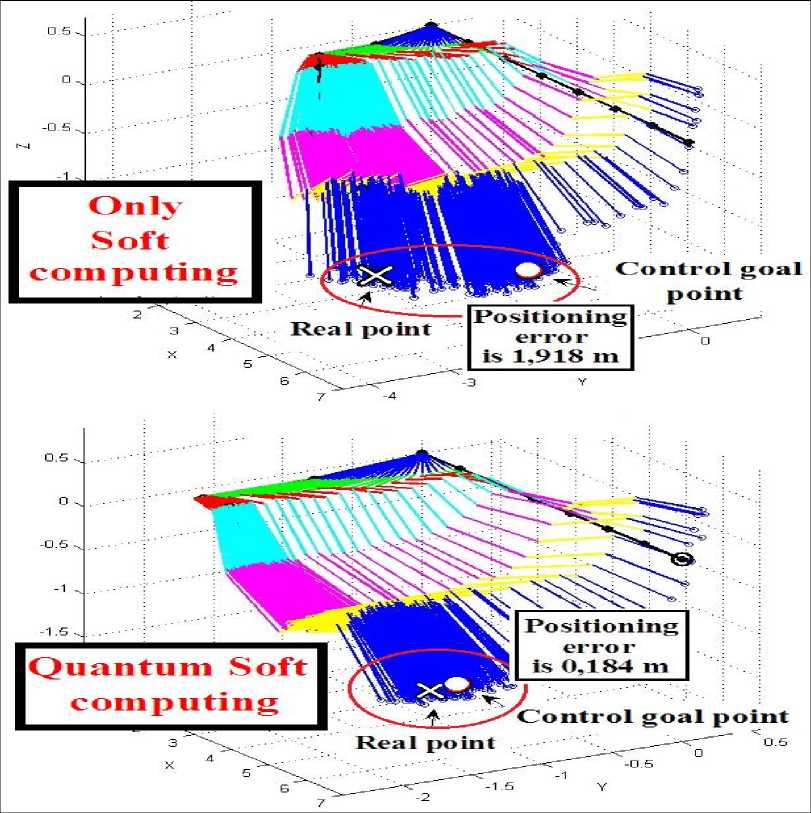
Figure 13. Manipulator behavior with random noise in the control channel

Consider the second internal unpredicted situation – random noise in the measurement system (see, the signal d ( t ) and «Sensors», Fig. 11). Comparison of Manipulator behavior for control system based on soft computing and based on quantum soft computing in performance criteria terms is shown in Fig. 14.

The results are demonstrating if ICS is used with QFI unit, all of evaluation of performance criteria improve (expect «One iteration time»).

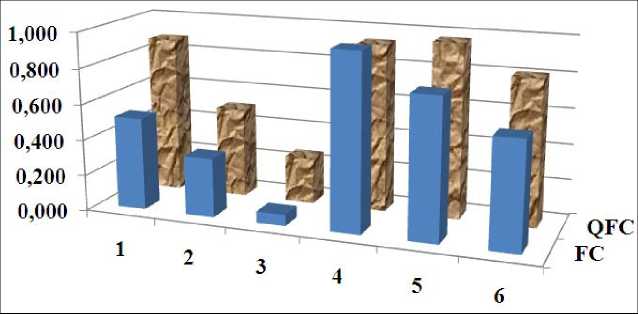
Figure 14. Manipulator behavior with random noise in the measurement system

The one of cases is shown in Fig. 15. Positioning accuracy is better if used ICS with QFI unit (in this case positioning error is 0.262 m). Positioning error is 2.519 m, if used ICS without QFI unit.

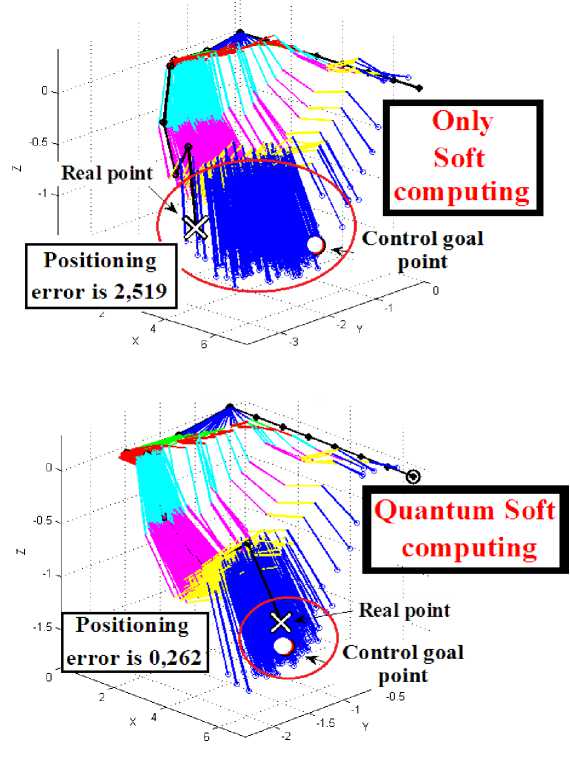
Figure 15. Manipulator behavior with random noise in the measurement system

Conclusions

Described approach opens new prospects for application of the model of quantum FC as the particular case of the quantum self-organization of KBs. The QFI introduction into control system with few independent KBs of FCs is allowed to improve control quality and robustness in unpredicted control situations that was presented on Benchmarks. QFI is a problem - independent programmable algorithmic gate. Thereby, it can be used in the different types of control system and embedded controllers. These facts present a great advantage, which manifests as the possibility of design of control with required robustness and accuracy in on line.