Quantum fuzzy inference model as quantum control algorithm of self-organization (minimum entropy principle relative to quantum knowledge)
Автор: Barchatova Irina
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 3, 2014 года.
Бесплатный доступ
The structure of quantum fuzzy inference (QFI) model that realize the self-organization process are considered. QFI is one of possible realization of quantum control algorithm of the self-organization processes that includes all of these features: (i) superposition; (ii) selection of quantum correlation types; (iii) information transport and quantum oracle (dynamic evolution); and (iv) interference. QFI model is introduced based on thermodynamics and information-theoretic measures of agent interactions in communication space between macro- and micro-levels (the entanglement-assisted correlations in an active system represented by a collection of intelligent agents).
Quantum fuzzy inference, quantum control algorithm of self-organization, knowledge base, minimum entropy principle, intelligent control, unpredicted situation
Короткий адрес: https://sciup.org/14123245
IDR: 14123245
Текст научной статьи Quantum fuzzy inference model as quantum control algorithm of self-organization (minimum entropy principle relative to quantum knowledge)
In control problems, the preservation of the property of operation robustness of a complex weakly structured (ill defined) control object due to application of intelligent control systems and intelligent computing is necessary condition for achieving the control objective in risk, hazard environments and contingencies (or off-optimum) control situations. From the algorithmic point of view, the efficient solution of the topical problem of providing stable operation of a control object in uncertainty conditions and preservation of ro- bustness of the intelligent control system means that in the applied algorithm of achieving the control objective the following necessary and sufficient (in the general case antagonistic) conditions are satisfied [1, 2]: (1) minimum of initial information on external environment (or perturbation acting on the control object); and (2) minimal consumption of generalized useful resource in the control object and intelligent control system. Therefore, the development of the correct algorithm of design of intelligent control system robustness is one of the topical problems of modern theory and control systems; this problem is referred to a complex and weakly studied field of development of intelligent control systems capable of efficient and reliable operation in risky conditions, contingencies, unpredicted and hazard environments [3–21]. The aim of this study is the development of information technology (IT) for design of robust KBs using quantum self-organization effects [2] in unpredicted and risky control conditions.
One challenge of control system design is achieving the control objectives in the presence of uncertainty. In control system design, there can be a tradeoff between achievable performance and robustness to uncertainty. For instance, increasing the performance of the closed-loop system can typically decrease robustness to uncertainty. Uncertainty can be associated with the control object, the environment, control objectives, the like, or any combination thereof. Control object uncertainty can include uncertainty in the parameters of the control object (for example, mass of the aircraft), in the dynamics of the control object (for example, unmodeled flexible modes of the wings of the aircraft), due to variations of dynamics over time (for example, due to component wear and/or fatigue), due to failures and damage (for example, sensor and/or actuator failures), the like, or any combination thereof.
Environmental uncertainty can include uncertainty in stochastic disturbances acting on the control object (for example, wind turbulence), sensor noise, sensor and/or actuator delays, the like, or any combination thereof. Control objective uncertainty can include uncertainty in a reference signal, changes in the control objectives after, for example, failures or faults (for example, after sustaining battle damage, an aircraft flight controller may relax its performance requirements in order to avoid aggressive maneuvers that may further damage the aircraft), the like, or any combination thereof.
A second challenge in control system design is compensating for risk by adjusting the controller gains, controller structure, control objectives, the like, and combinations thereof. Risk can include an occurrence of certain risk conditions and/or an information risk increment. Examples of risk conditions include, for example, actuator failure (such as an engine-out), severe environmental conditions (such as icing), hostile combat conditions, unreliable sensor measurements, and the like. The information risk increment can indicate the expected harm in relying on given information. For example, given a controller designed for a certain linear model of the control object, the information risk associated the controller can be the expected harm in using the control signal generated by the controller. Information risk increment can be based on the probability of a condition (for example, a probability that the controller is destabilizing), the expected loss if the harm occurs, observations (for example, sensor measurements), the like, or any combination thereof. When the information risk increment is large, it can be desirable to change the control structure and/or controller gains. Where the information risk increment is small, it can be desirable to utilize the controller. More detail regarding generating an estimate of the risk will be discussed below.
Because of tradeoffs between performance and robustness in situations with large uncertainty and/or information risk, conventional controllers may not be able to achieve satisfactory performance and/or stability for a number of variations of the uncertainty. A set of candidate controllers may be able to satisfy the control objectives in one or more of the number of variations of the uncertainty that conventional controls may not be able to achieve satisfactory performance and/or stability. If the set of candidate controllers can be constructed, a system can be configured to select a desired candidate controller online.
However, it may be difficult to construct the set of candidate controllers offline and/or online. First, the range of uncertainty may not be known. For example, in the context of an aircraft control object, it may be difficult to predict all variations of possible failure cases. Second, even if the range of uncertainty is known, it may be practically infeasible to design a set of candidate controllers to covers all possible realizations of the uncertainty.
To compensate for uncertainty and/or risk, an intelligent quantum tuning unit can construct and/or tune a controller by extracting knowledge from online data and from one or more knowledge bases. Knowledge bases can provide information concerning a specific subject matter. Examples of knowledge bases include controllers that provide information related to achieving the control objectives for the given measurements and for a certain realization of uncertainty. If there is a set of n candidate controllers, where n 2
Электронный журнал «Системный анализ в науке и образовании» Выпуск №3, 2014 год is a positive integer, a tuning unit can tune and/or construct a controller based on the combined outputs of n candidate controllers.
The result of development is guaranteed real time (on line) control in contingency control situations as a consequence of application of quantum control algorithm in the structure of the self-organized intelligent control system.
This article presents the principles of construction, structure, and practical application of the developed IT for design of robust knowledge bases of intelligent control systems capable of efficient and reliable operation in risky conditions and contingencies based on the self-organization model developed in [22, 24].
The structure of quantum fuzzy inference (QFI) model is described. QFI is a new quantum search algorithm (QA) and have realized the self-organization process. QFI is one of a possible realization of quantum control algorithm of self-organization processes that includes all of these features: (i) superposition; (ii) selection of quantum correlation types; (iii) information transport and quantum oracle (dynamic evolution); and (iv) quantum interference. QFI - model is based on thermodynamics and information-theoretic measures of active agent interactions in communication space between macro- and micro-levels (the entanglement-assisted correlations in an active system represented by a collection of intelligent agents). The (hidden) quantum value information is extracted from classical states of control signals with minimum entropy in “intelligent states”. From computer science viewpoint, the QA of QFI - model plays the role of the information-algorithmic and SW-platform support for design of self-organization process. Physically, the goal of the QFI algorithm is the support of the optimal thermodynamic and information trade - off between the control performance as stability, controllability and robustness in self - organization process. The main goal and properties of quantum control design algorithm of self-organization robust knowledgebase (KB) in intelligent control systems are described. The dominant role of self-organization in robust KB design of intelligent fuzzy controller for unpredicted control situations is discussed. Benchmark of robust intelligent control in unpredicted situation is introduced.
Example of efficient simulation of self-organization of robust KBs in intelligent control systems by dynamically unstable (with respect to generalized coordinates) essentially nonlinear control object is given. The model of control object is complicated by new (with respect to many known) constraints. In particular, the model of the control object contains in its structure random parametric perturbations, discrete constraints, contingencies, which represents a great algorithmic complexity for efficient application of conventional optimal control methods [23, 24].
Let us preliminarily discuss algorithmic specific features of quantum effects which reveal hidden information in classical states of control signals whose physical features and interpretation are considered in [25]. Hidden quantum information [26] extracted from classical states of control signals is used in the quantum design algorithm for efficient self-organization of robust KBs and is considered as the additional information resource.
Specific Features of Design of Self-Organization Properties of KBs Based on Quantum Effects
It was shown in [1] that in natural systems the sought robustness property is coded in the algorithm of reproduction of the self-organization process. Therefore, such systems can autonomously handle an unforeseen event using different (close, as regards the idea) approaches: (1) adaptation (learning, evolution) in the framework of which the system corrects its behavior in order to handle the event variation; (2) prediction (cognitivity) manifested in the fact that the system can “predict” the change of situation and determine more precisely its behavior (this property is a special case of adaptation and does not require that the system estimates the situation before it occurs); and (3) robustness consisting in the fact that the system can operate and achieve the objective if contingency perturbations of a certain type occur.
In natural systems, this property is achieved based on modular character, degeneration, distribution, or due to the excessiveness. Reliable operation of natural self-organized systems is provided by application of their separate properties, combination of above approaches and algorithmic formation of the complex of properties in changing or contingency conditions.
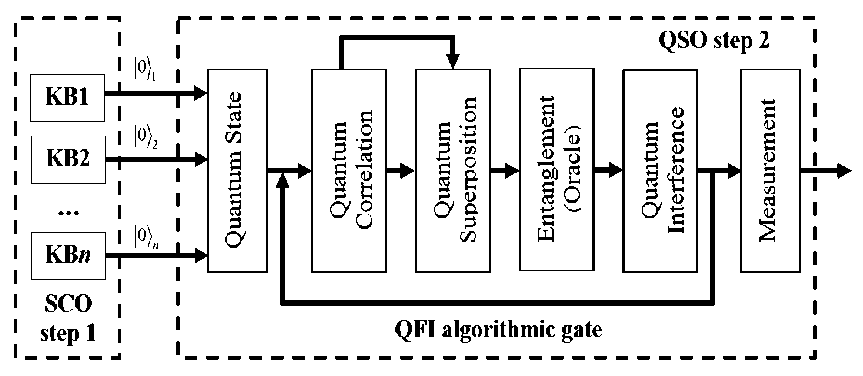
The robustness property of the KB is achieved by application of the quantum design algorithm of self-organization in the course of intelligent control which is schematically shown in Fig. 1.
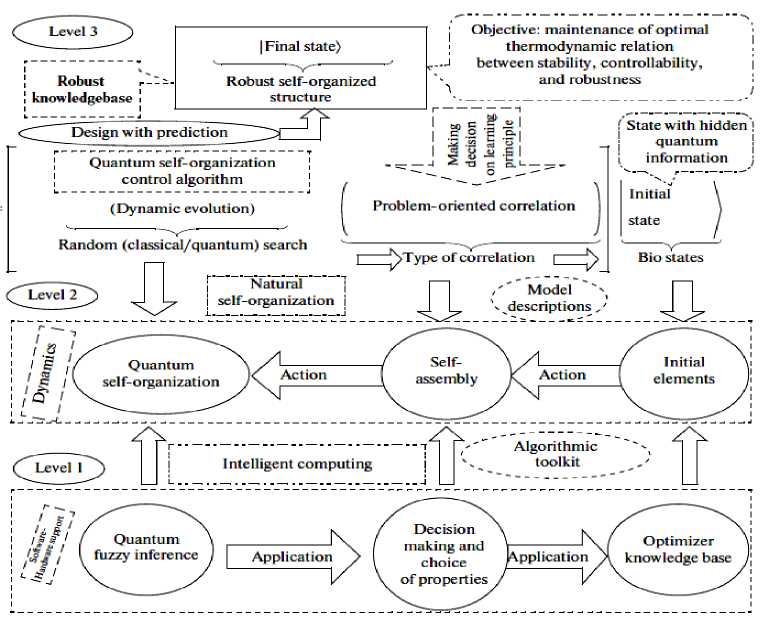
Figure 1. Hierarchical structure of quantum algorithm of design of self-organization of robust KBs in intelligent control system
The quantum algorithm is the part of the program structure of intelligent control system for realization of the required self-organization property.
Fig. 1 shows the hierarchical levels of the design process using the quantum algorithm, interconnection, and interrelation of the above self-organization properties of robust knowledge bases. The following levels of those shown in Fig. 1 were considered in detail in [1]: level 3 (physical model and objective of the self-organization control process, and physical interpretation of main operators of the quantum algorithm of knowledge base self-organization control), and level 2 (dynamics of evolution selforganization process).
It follows from Fig. 1 (see level 3) that in the general case of contingency control situations the process of design of optimal knowledge base using the information – thermodynamic criteria guarantees invariant real time reaching the control objective using the quantum self-organization algorithm with the required robustness level of intelligent control system. The proof of existence of this property was efficiently demonstrated in [27, 28] using the example of solution of the problem of optimal multi-objective criteria control in contingencies. The physical fact means that the optimal thermodynamic ratio between the stability, controllability, and robustness is preserved (see Fig. 1).
The process of design of robust KBs (Fig. 1) adequately corresponds to the above process of optimal support of introduced thermodynamic ratio between these fundamental control qualities (thermodynamics control quality trade off obtained in [1] as the physical self-organization criterion). It should be underlined that the effect of KB self-organization in the intelligent control system is based on the virtual process of extraction of additional (hidden) quantum information from the response (on the contingency) of classical control signals at the output of the KB designed in learning conditions [3] and is physically realized by the software toolkit.
The software – hardware support is shown in Fig. 1 (level 1). In this relation, let us elucidate the information properties and logical specific features of formation of the synergetic effect of self-organization discovered in [24] which is used in the software toolkit QCOptKB TM [25].
Information Processes of Formation of Synergetic Self-Organization Effects
The information synergetic effects of knowledge self-organization is the acquisition by the system of the required robustness property due to information (rather than direct physical) interaction of non robust KBs, i.e., the formation of the new quality in the united system which is absent in interacting subsystems making the whole1. This effect is realized by the process of information transfer and is the consequence of formation of virtual channels for transmission of quantum information between classical states of control signals.
This property is present in many quantum systems. Some of existing unusual physical phenomena which include the synergetic effect similar to that applied in this study were considered in [28 – 31]. In particular [31] contains the discussion of an interesting elucidating example: two subsystems each of which is in the mixed chaotic state (with nonzero maximal entropy) upon merging into one system form the pure (with zero entropy) state possessing higher order level (effect of quantum self - organization). In this case, the amount of information in the whole system is smaller than in each of its component subsystems. However, the classical subsystem by definition should be in the pure state in the united system, and for quantum system this requirement is not always satisfied. The paradox is that the entropy of the whole system is equal to zero, while the entropies of two subsystems are positive and have a maximal value of 1.
This fact means that the information contained in the whole system is smaller than the amount of information present in each of the subsystems. Elucidation of the physical meaning and specific features of this effect which can be difficult for comprehension and interpretation (from the point of view of Boolean logics) in relation with the development of processes of extraction of quantum information from classical states is given in [31]. This specific property of the structure of quantum states was formulated by Schrodinger as follows: “The best possible knowledge of a whole does not necessarily include the best possible knowledge of all its parts ”.
It is remarkable that this paradox can be solved due to an even stranger property (from the point of view of Shannon’s information theory), negative value of conditional entropy. Experiment proved the theoretical statement that two interacting subsystems in this case are found in mixed states with nonzero entropies. In this case nonclassical physical properties of nonlocal superposition with quantum correlation between subsystems as the mathematical object result in the paradox of violation of elementary arithmetic rule in the form 2 ≠ 1 + 1. Physical realization of the quantum state of superposition in electron nanostructure (“quantum coral”) with this property of transfer of quantum information by wave functions of subsystems is described in [32] (see complete analysis in [33]). Only statistical knowledge can be obtained by measurement from these subsystems.
Therefore, unlike the classical Shannon’s information theory, von Neumann quantum conditional entropy can take negative values if entangled states are considered. This fact is directly connected with quantum inseparability of entangled states, and they are interpreted as gigantically correlated (super-) states.
Thus, the negative character of conditional entropy indicates the presence of entangled states in the compound quantum system and determines the lower boundary of their correlation. The latter means that information on the state of the compound system is not maximal, and subsystems have more chaotic behavior than the compound system [34]. This property is used in the model of QFI in extraction of additional quantum information from classical control signals.
Therefore, information analysis of uncertainty in the state of the compound quantum system makes it possible to clearly explain the presence of unusual (nonclassical) properties: ignoring part of information on the state of subsystem results in the growth of quantum uncertainty.
As a result, the amount of quantum uncertainty in the “part” (subsystem) is larger than in the “complete” (compound) quantum system. This effect is absent in classical systems due to the properties of measure of Shannon’s information entropy. This strange for classical systems property, for which complete information on the compound system (zero entropy) is available, and only part of information on subsystems, characterizes the capability of quantum systems to self - organization due to the application of the property of super correlation (quantum correlation) contained in entangled states. It is due to the presence of quantum correlation of mixed compound states that it is possible to form the pure state.
This result characterizes the special property of synergetic effect inherent to the quantum compound system and absent in the classical system. This fact testifies the deep difference between classical and quantum states [26].
Therefore, excessive amount of information hidden in subsystems can be extracted and used as the additional information resource. The described information self - organization effect and found capabilities (additional amount of information due to quantum correlation) are applied in the model of QFI in formation of the robust control signal from two non robust signals using new types of quantum correlation.
Let us discuss the specific features of quantum control algorithm for the self-organization process shown in Fig. 1 (levels 2 and 3) from the point of view of complexity of quantum computing and software support of control processes of knowledge self-organization.
Generalized Structure of Quantum Control Algorithm of Self-Organization
The structure of the quantum control algorithm of self-organization (Fig. 1) involves all (necessary and sufficient) actions and operators (operators act from left to right) characterizing it as belonging to the class of quantum search algorithms [25]. From the point of view of the theory of quantum computing and algorithms the structure of quantum algorithm contains a number of specific features and actions: (1) preparation of the state of quantum superposition; (2) choice of the type of quantum correlation (in this case the determination (of the type and form) of quantum correlation depends on the class of nonlinearity of the control object); (3) application of operator of quantum oracle («black box» model); (4) exchange of partially extracted (hidden) quantum information between components; (5) dynamic evolution of «intelligent» quantum state by the criterion of minimum of information entropy; (6) application of quantum correlation as the alternative to classical correlation, which is considered as the additional resource of quantum algorithm; (7) application of the effect of massive parallel quantum computing; (8) introduction of the principle of amplification of probability amplitude of the sought solution; and (9) application of the operator of structural interference for extraction of the sought (found) solution.
These effects are achieved using quantum operators, which act in the interactive regime depending on the type of quantum algorithm. The number of iterations depends on the criteria of accuracy and termination of quantum algorithm. The mathematical model of self-organization is described on the qualitative level in the form of the following quantum algorithm [24]:
Final ordered state
Self - organizationof robust structure
Problem orientation of control object । Evolution of self- ]
I organization process J | Quantum | ZZ ZTT7 \
У b _______ 1 _______/ • I I • ( Type and form of correlation )
^ computing } --------------v--------------'
Quantum random search
Classical, quantum, mixed
|
"Building"blocks' |
|
|
< | Initial state) |
( Reproduced by given or ^ natural toolkit |
^Bio-inspired states where (•) means the application of the corresponding toolkit or operation (operators act from right to left).
At the first stage of algorithm (1) the knowledge base optimizer with soft computing is used to create the «building» blocks of knowledge self-organization based on the genetic algorithm in the form of control laws for the gains of the fuzzy PID controller on the basis of production rules of the knowledge base. The obtained trajectories of the control law are considered as the classical states, the chaotic paths of the intelli- gent collective motion of particles in the «swarm» with information interaction (swarm intelligence) which is one of the efficient methods of algorithmization of quantum models of description of the collective particle behavior (swarm method of collective particle behavior) [29]. Under certain assumptions the swarm method has the computing complexity of the simulation algorithm [3] of the dynamics of collective particle interaction with linear dependence on the number of particles, which yields great advantages in the case of constraints on the memory and time of simulation.
Let us consider (without losing generality) the simple case of two trajectories of the control laws of gains; these trajectories belong to the set S and S . According to (1), the superposition of the classical states on the set S = S S forms the unified quantum state in the form:
ψ S )= ∑ λ j ψ S j 1 ⊗ ψ S j 2 , (2)
j where ψ1 , ψS21 , и ψ1S2 ,
ψ 2 form the orthonormal computing basis in the space of states S and
S , respectively. Physically (2) is considered as one state in which entangled states are formed from the process of particle motion along classical trajectories due to the information exchange.
Fig. 2 shows the process of information exchange via quantum connection channels [35] between particles on the trajectories A∈ S and B∈ S. Here, the mediator М is the compound quantum object with the finite memory dimension d uniting three subsystems M, M, and M using the Hamiltonian H. The mediator M is the efficient channel which connects two different parts, the source of message А and the receiver of information В. In this case, А is supported by the quantum register A and B, respectively. The quantum register possesses partially ordered memory a,a, . The source А sends the message to В which is stored in the quantum memory a , a , , a , connected with the subsystem M of the mediator М; each memory element M contacts once, following the order indicated in Fig. 2 (shown by the arrow, i.e., first a , then a , etc.).
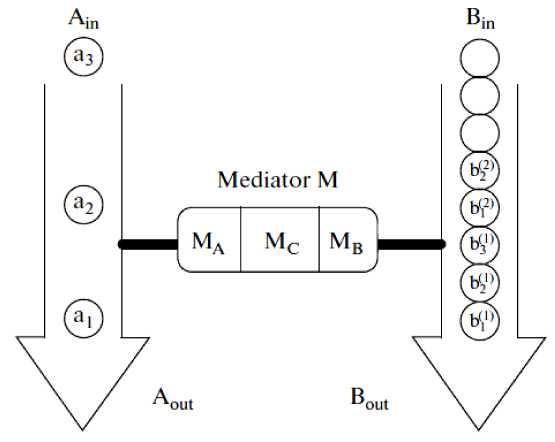
Figure 2. Information exchange process via quantum channels
The receiver B , having received the message from А , forms the memory b using the corresponding state v and is united with the subsystem M of the mediator М , following the order shown in Fig. 2; in this figure, A and B mean the input ports of devices used by A and B for transmission of q - bits at the contact with M . Similarly, A and B mean the output ports where q - bits are formed after the contact with the mediator M . It was shown in [2, 3] that the state of such quantum connection channel forms the unified quantum state with the mediator, and the particular spur of the density matrix (together with the density matrices of the source А and the receiver В ) is superposition (2) in the form of Schmidt decomposition in the
computational basis. In this case in the quantum information theory [34] quantum connection channels are used to transmit superposition of signals (2) with preservation of different types of correlation between agents.
-
D. Physical interpretation of quantum algorithm of self-organization control. From the point of view of the process of biologically reproducible evolution of self-organization at the first stage of application of the quantum algorithm (1) the superposition operator implements the procedure of formation of the set of non connected elements of the structure in the form of «building blocks» (templating) and codes the sought solution. In this case, the procedure of interaction of elements of micro- and macrolevels with information exchange between active agents is formed.
Remark. It should be mentioned that here, following the ideas and definitions of the self-organization theory [4 – 9] the active agents of the macrolevel [11, 12] are the current values of the control process obtained as a result of reaction of robust knowledge bases of the fuzzy controller. Active agents of the microlevel here are the virtual values of the control process obtained as a result of application of the quantum principle of complementarity to real values of the control state on the macrolevel.
Remark. There exists a «paradox» stating that self-organization contradicts the second thermodynamic law according to which the system evolution tends to chaos (entropy growth). This «paradox» was resolved [13, 14] in terms of multiple interactions of macro- and micro-levels of evolution (open thermodynamic system) of self-organization and decreased entropy production on the macro-level (ordering growth) due to increased entropy production on the micro-level (behavioral chaos growth).
The choice of the type of quantum correlation realizes the self-assembling of the required structure using the resource of interaction via communication and information transmission on the micro-level [27, 35]. In this case, the type of correlation determines the level of robustness of the intelligent control system. In this application of the quantum oracle, the «intelligent» quantum state of the self-organization structure, which contains valuable information for application and implementation of coordinated control, is calculated. The interference is used for extracting the results of coordinated control and robust knowledge design.
The particular model of the quantum algorithm of self-organization control based on the quantum fuzzy inference and its application in the technology of robust knowledge base design was considered in [24] and discussed below.
In particular, the following example was given: the quantum self-organization algorithm (based on the self-organization of the behavior of the swarm of people in the tunnel) for (real time) formation of knowledge based on robust knowledge bases in fuzzy PID controllers under the conditions of uncertainty of initial information and contingency control situations.
-
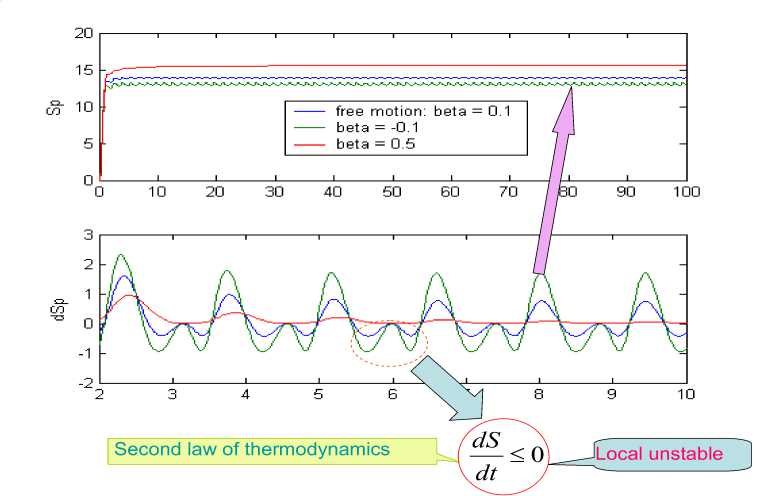
E. Application goal of quantum control algorithm of self-organization. Fig. 3a shows the main thermodynamic relation of the quality of robust intelligent control and the optimization criterion used in the quantum self-organization algorithm [22].
Remark. In Fig. 3 the following notation is used: V - is the Lyapunov function; ScOS Sc - is the entropy production in the control object and the controller, respectively;
n
-
V = 1 1 q i +
— S 2; S = Sc-- Sc ; qt = ^ ( qt , u,t ) are the motion equations of the control object; Sv vN is the
-
2 i = 1
von Neumann quantum entropy; ^ is the wave function; and p is the event probability. The derivation of relations in Fig. 3a can be found in [1, 2, 27].
Fig. 3b illustrates the details of the computational process of the choice of «intelligent» quantum state for the principle of minimal Shannon information entropy (maximal probability amplitude). In the course of evolution of self-organization the balanced relation between the used and potential resources of evolution of the (information–thermodynamic) behavior of the dynamic system is achieved [3].
Note the following aspects of development of the self-organization model: (1) the goal of the developed quantum algorithm of knowledge self-organization control is achieving the thermodynamic criterion (see Fig. 3a) of the optimal relation between the stability, controllability, and robustness which is used in real time in the control loop [2, 24]; (2) the principle of minimal generalized entropy of the «dynamic control object + controller» system provides simultaneous achieving the global robustness and implementing the optimal intelligent control with minimal loss of the useful energy resource [1].
-
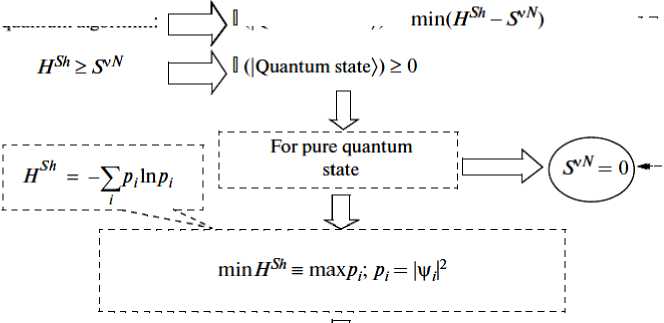
F. Difference of the model of quantum control algorithm of self-organization from biologically reproducible evolution of self-organization. The main differences are: (1) the quantum algorithm of selforganization control is described as the logical process of application of valuable quantum information extracted from classical states using quantum decision making strategies and facts of quantum information theory; (2) it contains the choice of the type and form of quantum correlation which influence the formation and form of the structure of the designed system; (3) structurally the quantum algorithm includes all necessary qualitative specific features and operators of natural (biologically reproducible) self-organization, which are described by quantum operators of the theory of quantum computing; (4) it is a new search quantum algorithm, which can be used to solve classically algorithmically unsolvable control problems; (5) it is implemented in real time using the reaction of classical fuzzy controllers on the new control error in the contingency control situation for the robust intelligent control design; and (6) it supports optimal thermodynamic relation between the stability, controllability, and robustness for real time design of intelligent self-organized control processes.
Closed system
Open system
Qi
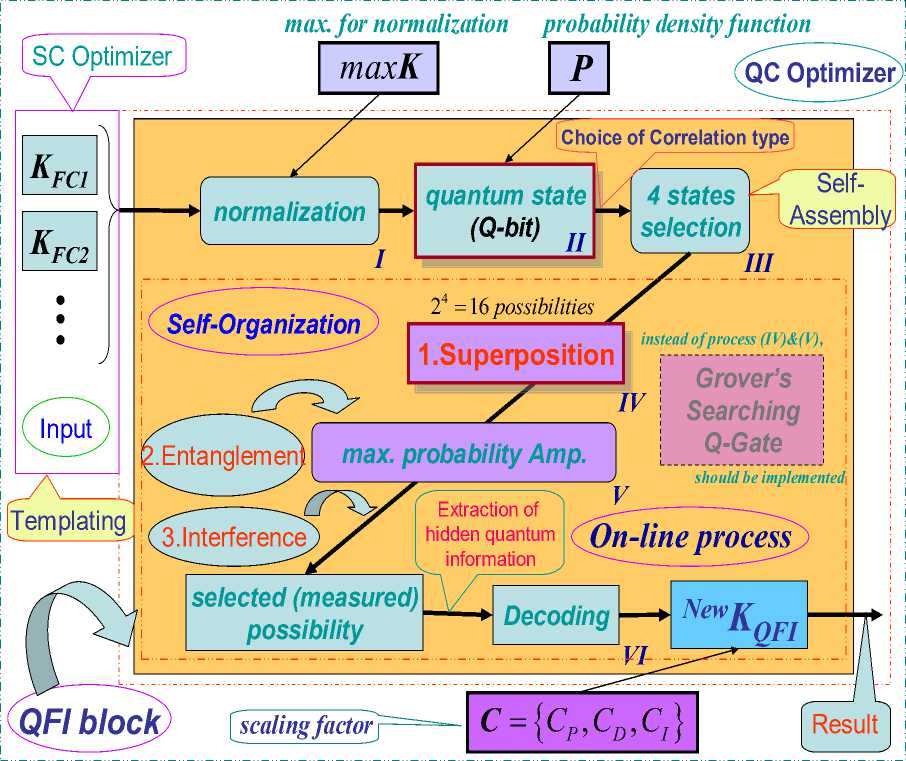
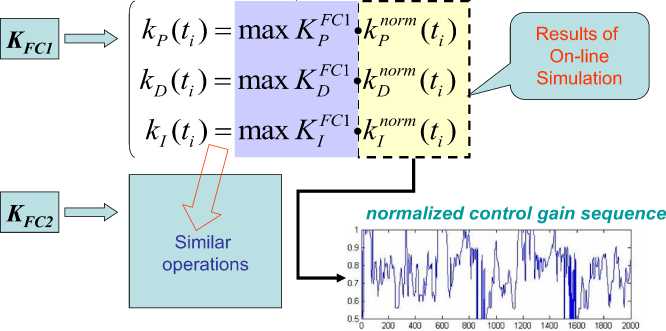
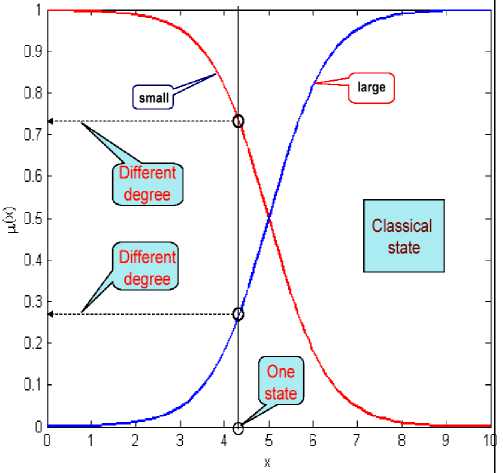
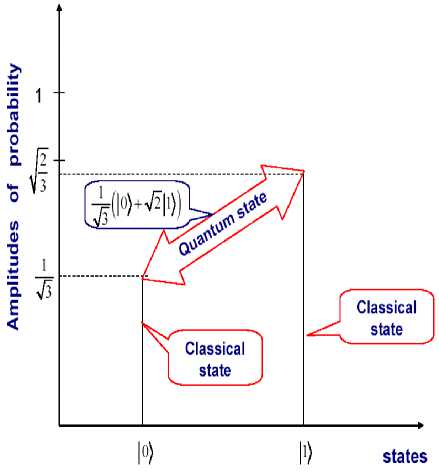
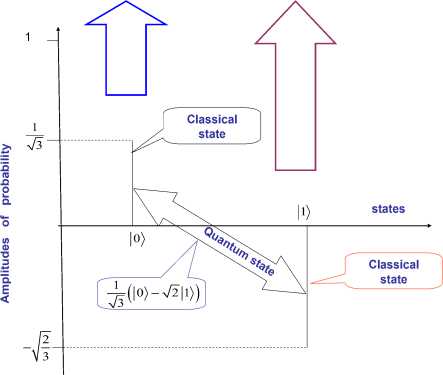
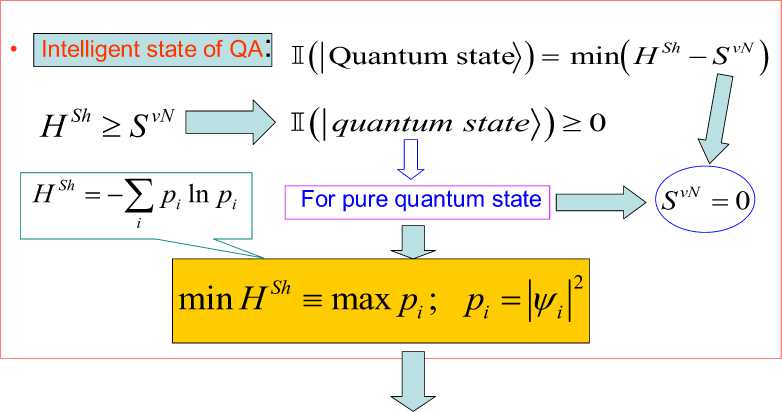
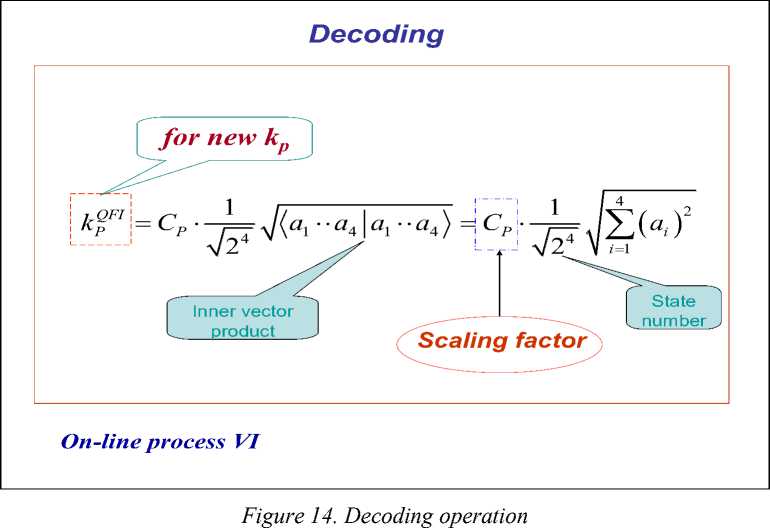
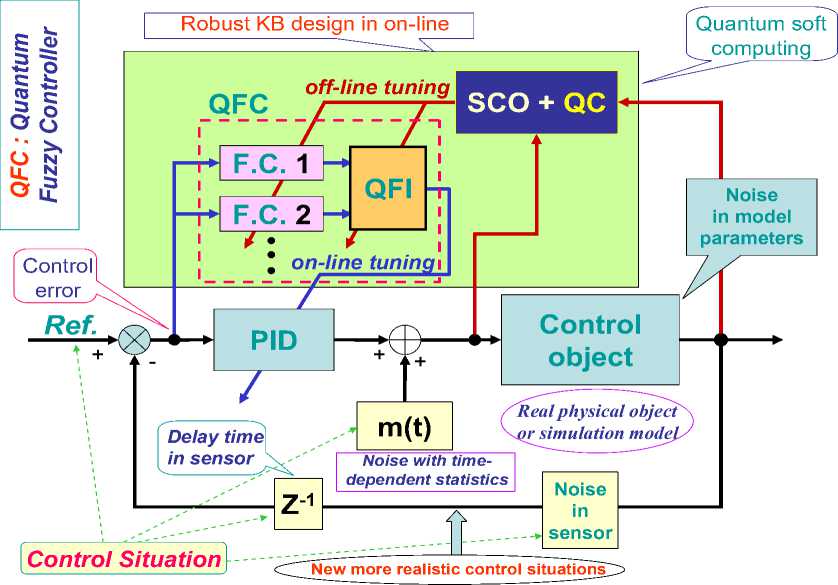
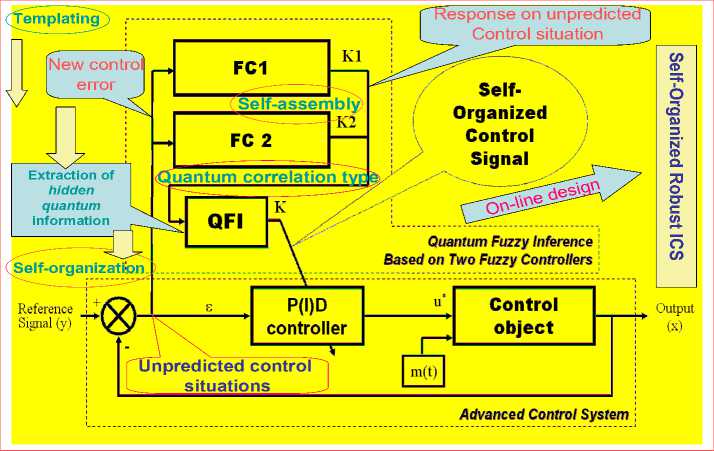
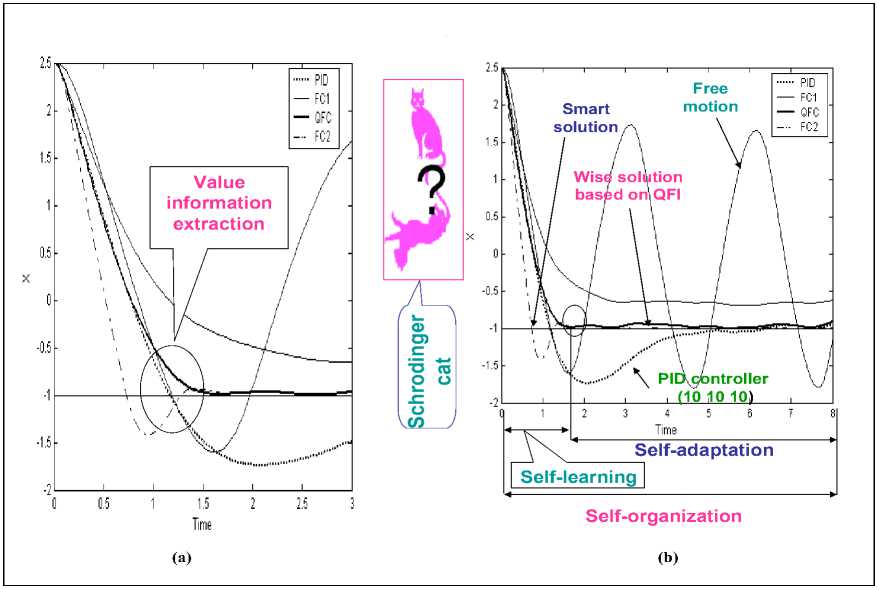
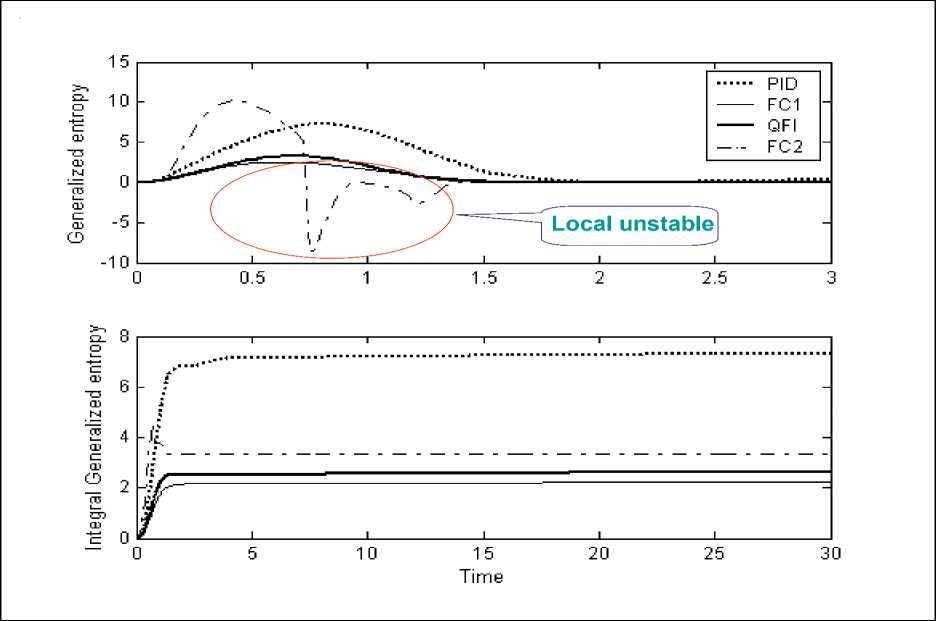
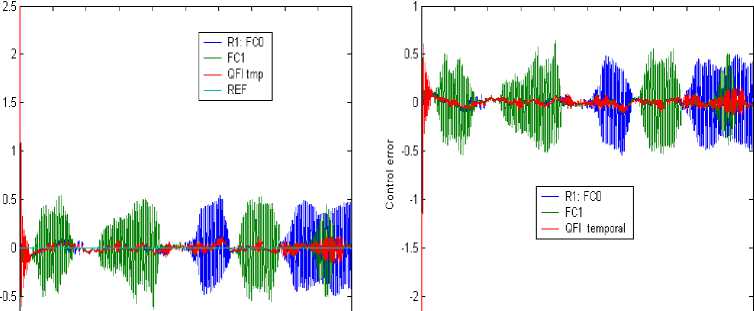
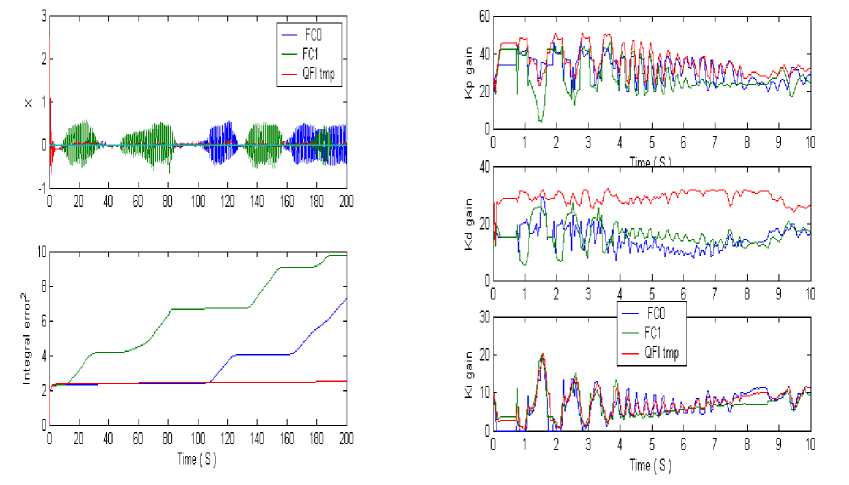
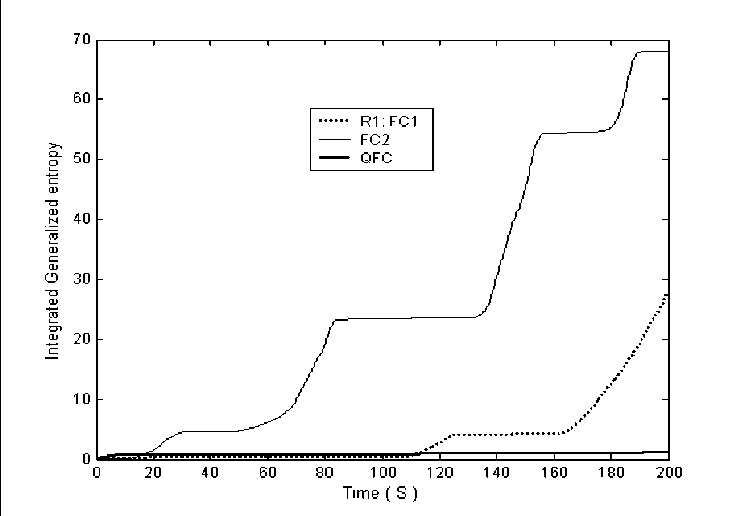
= 0 Control object Lyapunov function dV _ |<^co Tdt Thermodynamic relation between stability, controllability, and robustness 0 > S' = £»-" V(^ «. о + (Sco - 5c)(^CO -^C) Stability Control object dynamics Thermodynamic behavior condition (controllability) of control object (robustness) Generalized measure of entropy production (a) 1 ([Quantum state)) = Intelligent state of quantum algorithm: H^W = -logtmaxP^)) Principle of minimal entropy with respect to quantum knowledge Oracle in quantum fuzzy inference algorithm chooses the intelligent state using the maximal probability amplitude, which is equivalent to the minimal Shannon entropy (b) Figure 3. Robust control quality design: (a) thermodynamic quality criterion of robust control; (b) choice of «intelligent» quantum state Therefore, the quantum algorithm of knowledge self-organization control (1) contains the physically grounded and experimentally established quantum operators and is related to the new class of search quantum algorithms depending on the choice of the type and form of the problem orientation of quantum correlation. As a result, in the general case the solution to the classical algorithmically unsolvable problem is achieved based on application of efficient quantum decision making strategies. Let us consider particular case (1). Quantum Algorithm of Knowledge Self-Organization Control The mathematical model of quantum algorithm of knowledge self-organization in production rules of knowledge bases of hybrid PID controller follows from (1) as a particular case of quantum algorithm of selforganization and has the following form: Control laws for gains of fuzzyPID controller • ( Output) Self-organization of robust structure of knowledge base (Inference)[max (of probability amplitude)](superposition) z Quantum v computing • Quantum random search Problem orientation of control object < Choiceof type and form of vquantum correlation ? Typeandform of correlation v(External, internal) • (Classical, quantum, mixed)^ Formation of quality and depth of knowledge representation "Building"blocks Initialstate State of output of fuzzy ^Reaction of production rules of knowledge vbase in fuzzy controller with soft computing , (Input) • (Control error in contingency ) contoller for new control error Model (3) describes the mathematical structure of quantum fuzzy inference developed in [3, 22–24]. Therefore, the model of quantum algorithm in quantum fuzzy inference is the particular case of generalized model of quantum self-organization algorithm presented in Fig. 1 (level 3). Let us consider briefly the mathematical specific features of stages and numerical aspects of quantum algorithm (3) in the model of quantum fuzzy inference for design of robust knowledge bases based on synergetic self-organization principle. At the first stage of algorithm (3), optimizer knowledge base with soft computing is used to create “building” blocks of knowledge self-organization based on genetic algorithm in the form of control laws of gains of fuzzy PID controller using production rules of knowledge bases. The obtained trajectories of control laws are interpreted as classical states, chaotic paths of intelligent collective motion of particles in the “crowd”, with information interaction (swarm intelligence) and information exchange. This description is one of the efficient methods of algorithmization of quantum models of collective particle behavior (swarm method of collective particle behavior) [3, 29]. Fig. 4 describes programmable algorithmic gate of QFI realization of which can be implemented using both classical and quantum computer, and can also be integrated into different control system and embedded intelligent controllers. Figure 4. Quantum algorithmic gate of QFI realization Let us illustrate this approach using the example. QFI: Structure and applications to robust KB design Main problem solution of QFI is on-line design of robust KB for unpredicted control situations from individual KB (that are designed for concrete control situations with soft computing technology and stochastic simulation). The QFI is based on the physical interpretation of self-organization process on quantum level: on the model of the exchange, extraction, and transfer of quantum hidden information from/between classical particle’s trajectories in particle swarm and new types of quantum correlations between particle swarm trajectories. Structure of QFI is based on QA that includes superposition, entanglement, interference quantum operators, and new types of quantum correlations [3]. The structure of QFI was developed in [22, 24]. The (hidden) quantum value information extracted from classical states with minimum entropy in “intelligent states” of control signals. From computer science viewpoint, QA of QFI model plays the role of the information-algorithmic and SW-platform support for design of self-organization process. Physically, QFI supports optimal thermodynamic trade-off between stability, controllability and robustness in selforganization process. The dominant role of self-organization in robust knowledge base (KB) design of intelligent fuzzy controllers (FC) for unpredicted control situations is discussed. We will discuss the main goal and properties of quantum control design algorithm of self-organization robust KB in intelligent control systems. The dominant role of self-organization in robust knowledge base (KB) design of intelligent fuzzy controllers (FC) for unpredicted control situations is discussed. Benchmark of robust intelligent control in unpredicted situation is introduced. Let us consider the functional structure and work principle of main boxes in QFI as the Level 3 in Fig. 1. Structure of quantum fuzzy inference model and operator’s description Fig. 5 shows the structure and main boxes of QFI. QFI includes the following steps: 1. Normalization 2. Quantum state with hidden information 3. Choice of correlation type 4. Selection of state type 5. Superposition 6. Entanglement (Quantum oracle) 7. Interference 8. Measurement (Decoding). Figure 5. Structure and main boxes of QFI And correspondingly main boxes are included: (I) Normalization; (II) Quantum state (Q-bit); (III) Choice of correlation and selection of quantum state; (IV) Superposition state with hidden quantum information; (V) Quantum oracle; (VI) Decoding. Let us briefly discuss main physical meaning and box structure of QFI in Fig. 5. As example we will discuss (without loss of generality) the process of extraction of hidden quantum information, data processing, and design of robust KB for fuzzy PID-controller. We will use KB of two individual FC that was designed in off-line for two fixed (different) control situations. As inputs QFI is used in on-line the signals of two individual KB (KFC1, KFC2) from SC Optimizer. In this case SC Optimizer organizes the Templating as the finite set of control signal trajectories of coefficient gain schedules in corresponding fuzzy PID-controllers. This step is corresponded to the «Initial states» and «Templating». Next step is normalization process that shows in Fig. 6. This step includes the algorithmic operation as dividing on maximal amplitudes of amplitudes of corresponding control trajectories (Box « max K » and together with Box I in Fig. 5). Next step is design of corresponding quantum states. Figure 7 shows the main computing algorithm of quantum state based on the definition of quantum superposition [34]. In our case the space of states of subsystems is superposition of KB1 and KB2. Control laws of coefficient gain trajectories of fuzzy PID controllers designed on Soft Computing Optimizer (SCO) are included the important information about optimal control of control object in concrete (fixed) control situation. Coefficient gain trajectories of fuzzy PID controllers are considered as a random motion of particle swarm [3]. The physical interpretation of self-organization process on quantum level is introduced based on the model 12 of the exchange and extraction of quantum hidden information from/between classical particle’s trajectories in particle swarm. Normalization On-line process I maxK FC1 Figure 6. Normalization process Computer Science Interpretation Physical Interpretation quantum state Templating On-line process II probability distribution function Calculation 0.6 0.4 Hidden quantum information — I (х) - НЮ (у'.)2 = P {11., P} Quantum complementary 0^-----'- 1 0.5 0.55 0.6 0.65 0.7 0.75! 10.8 0.3 0.95 1 P {1#}=1 - P {l °\p } w 1, P 1, P control gain sequence ti Virtual state Real state ^T- qubit : quantum superposed state for k at t kFC^=^(yy0P'! °^ i, p Figure 7. Computing algorithm design of quantum superposition state New types of quantum correlations between particle swarm trajectories are introduced (see, Fig. 5, Box II and below). In Fig. 5, Box II together with Box III are design the superposition state and play the self-assembly role. For more deep understanding of physical meaning of QFI let us consider the physical peculiarities and differences between the definitions of quantum superposition and classical environment states on fuzzy set. Example: Quantum superposition. In fuzzy set theory physical state is mapping (by expert) on linguistic scale (generally in subjective form) as linguistic variable. Figure 8 shows the case description for linguistic variables «large» and «small» describing the physical state 4.28. According to the definition of fuzzy set theory the state «small» is described as 4.23/0.79 and the state «large» is described as 4.23/0.21. Figs 7 and 8 are demonstrated the difference between fuzzy and quantum states. Figure 8. Fuzzy sets for linguistic variables “small” and “medium” Figure 9. Quantum superposition of two classical states Thus one number (as physical state) is characterized by two linguistic variables and can have the interpretation as «small» with membership degree 0.79 and as «large» with membership degree 0.21. In this case linguistic variable «large» is described by membership function ^ that can be defined through membership function ^m of linguistic variable «small» as ^ = 1 - ^m, i.e. includes the law of negation. It is important that for this case the law of middle excluding is valid, and the fuzzy state is non-measurable. In quantum mechanics quantum state consists from two and more classical states with fixed amplitudes of probability and physically means one observable state (on the quantum mechanics language is called “observable”). Figure 9 shows quantum superposition state of two classical states «large» and «small». Figure 10 demonstrate the physical meaning of quantum superposition with different classical states as hi (| 0) + V2|1)) and -1^ (| 0) - V2|1)), correspondingly. Figure 10,b shows that amplitude of probability in quantum mechanics can be negative and characterize the non-Kolmogorov’s property of classical probability theory. (a) (b) Figure 10. Physical interpretation of probability amplitude of quantum states The essential difference between quantum superposition and fuzzy state is the result of measurement. In quantum mechanics the result of measurement (in fixed measurement basis) is one classical state with maximal amplitude of probability. Other classical states in superposition are non-accusable for observer. Quantum superposition state is objective state and observed in many experiments. For quantum superposition we have complementary law that as partial case includes the logical negation law. For example, for quantum superposition in Figs 8 and 10,a of the states 1 »large» and 0 «small» as —(|0) + 2111) the probability law gives: 3 = 1 . Z p = i=1,2 Fuzzy set theory also gives ^ + ^m= 1. But linguistic variables 11) «large» and 10) «small» in quantum superposition have different numerical values and differs from the case of fuzzy state that have only one (crisp) value. In quantum computing calculation process starting from action of evolution operator U on “initial” state 00 0 as unitary generalized Walsh-Hadamard transform: Uf =®Uf (i) Электронный журнал «Системный анализ в науке и образовании» where Uf (‘) = fW) - 1- f(i) ,V1 -f(') fi) , and ^f (i) define amplitude of probability of i th classical state in quantum superposition. As result we have the following: Uf 100.. .0) = pz^ , where |s^ define the superposition state from finite number of classical states. Thus every operator U maps qubit from initial state in mixed superposition state with fixed probability state f (i) . Geometrically operator U.^ is Bloch sphere with rotation around y axis on angle ^ = 2arcsin (f (i)). This approach can be used also for design of quantum fuzzy states when the analogy of probability marginal function plays a membership function [36]. Thus after signal normalization the operation of quantum bit’s forming is applied (Box II, Figure 8.2) from current values of normalized control signals. For this case probability density function is advanced calculated using representative trajectories of control signals. After integration the probability density function integral probability functions are received (Boxes «Р» and II, Figure 8.2). The defined integral probability functions are used for definition of «virtual» classical states 1 of control signals for design of superposition states using Hadamard transform (4) from current values of control signal inputs in QFI. Probability law as P(| 0)) + P(| 1)) = 1 is used, where P(| 0)) and P(| 1)) are current probability values of real and virtual states of control signal, correspondingly. According to description in Fig. 5, for the current normalized control signal 0 with integral (marginal) probability function his probability state is defined. As example, in Fig. 7 for numerical normalized real state 0 as 0.92 we have the probability state 0.8. Then we can define the probability of virtual normalized state |1) using calculation 1 - 0.8 = 0.2 and using same marginal probability function with inverse mapping calculate numerical value of corresponding virtual control signal. In our case the result is 0.63 (but 0.92 + 0.63 ^ 1 and we are used quantum principle of complementary, and do not can use the law of logical negation as 1 - 0.92 = 0.08). Therefore the superposition of quantum system state «real state – virtual state» has the following form: I ^=^ (#0°) 1°)+J1 -P (I ■) 10 )= quantum bit (qbit) . Figs 5 (Box IV) and 11,a show the design process of quantum superposition states from classical states of coefficient gain schedules of used two KB of fuzzy PID-controllers and fixed type of quantum correlation. In this case three types of quantum correlations between individual KB (that include hidden value information) are considered: spatial; temporal; and spatiotemporal. Figure 11,b show these three types of correlations between control law processes of two PID coefficient gain’s schedule. Figure 11,b show the example of spatial correlation design in QFI from control coefficient gains signals of two fuzzy PID-controllers. Superposition On-line process IV for new kp (superposition of 4 selected quantum states) kF”) /Л ^®| к FC1 'J .k "J Quantum superposed state = (y0P 'I °\. P + -^l, P 'I 01. P )« ^ (y ", P 'I 02, P+y 2, P ■ I 12, P ) « ( ytD "‘D + y‘D • ‘1,B ) « (y "D • "^ + У\d 12,B ) ^l^6sss^siitiHSes (n = 4) 0 0 0 0> . a‘ = y‘,P ' y2,P ' y‘,D ■ y2,D • 1= («1 -10000) + a" -10001) + • • ■ + an , -| 1110) + an • 1Ш0) 2" aa probability amplitude Figure 11, a. Computation algorithm of superposition states for proportional coefficient gain k [On-line process IV for new k (superposition of 4 selected quantum states)] Figure 11, b. Types of quantum correlations KB of these controllers is designed by SCO tool for two different control situations. Quantum spatial correlations (as type) classified on two classes of correlations: internal and external. Figure 11,b also shows these two classes of correlations. Internal quantum correlation is organized by statistical properties of first output control signal’s FC1 of coefficient gain schedule K . External quantum correlation is organized by corresponding statistical properties of first and second output control signal’s FC1 and FC2 of coefficient gain schedules K and K , where index « FC1 » means first FC and index « FC2 » means second FC. Figures 9 and 11,c show that new proportional coefficient gain knFC with spatial correlation is nFC FC1 FC2 FC1 FC2 kP =|kp ^®kp 2® kD /® ki) /, and includes the information about proportional and differential coefficient gains. Thus k"pC is behavior coordinator of four active agents {k)C 1^,|k)C2^,|k)C 1^,|k)C2^} and include value control information as response of these agents on unpredicted control situation. Figure 12 shows computing steps after superposition state design (see, Fig. 9). 4 states selection based on a type of QFI Self-assembly On-line process III for new k for new k for new k KFC1 KFC2 FC1 kD kFC1 kp kD kI Figure 11, c. Spatial (internal and external) quantum correlation between coefficient gain’s signals of two fuzzy PID-controllers Similar results as in Fig. 11,c are for temporal and spatiotemporal correlations. Therefore, the coordination control between coefficient gains is realized by design of different correlation types with different classes of internal and external correlations. Thus for discussed example of two fuzzy PID-controllers every quantum superposition state of designed coefficient gain is described with four qubits. Box “Oracle” calculates all amplitudes of probability of 16 classical states and recognize the maximum amplitude. Figure 13 shows the selection by maximum probability amplitude for new knFC . This Box plays the role of interference. FC1 Quantum superposed state ClassicalState 2n a-| 0000)+a • |oooi) + • • ak J ax a2 a3 a4) selected maximal possibility state max. quantum correlation ai a a •+ a„ч • I1110)+aT probability amplitude = yl,P ‘ y2,P ' yl,D ' y2,D = yl,P ‘ y2,P ‘ yl,D ‘ y2,D 16 yl,P ‘ y2,P ' yl,D ‘ y2,D Oracle Figure 12. Selection by maximum probability amplitude for new knFC (Superposition of 4 selected quantum states) Why maximum of amplitude probability? Oracle of QFI algorithm choice the intelligent state with maximum amplitude probability that equivalent to the minimum of Shannon entropy Figure 13. Selection by maximum probability amplitude for newk nFC Figure 14 show the decoding operation. Thus quantum random search operators of self-organization process are as following: superposition; oracle; interference; and decoding (measurement). These quantum operations are used in QA of QFI and simulation of robust KB. Quantum algorithm of hidden information extraction: selection and peculiarities Let us consider from quantum information theory viewpoint other details of QA for hidden quantum information extraction from superposition state (see, Figs 10 and 12). Without loss of generality we consider one way communication between players A and B with fixed amount of hidden (unobserved) classical correlation in quantum state. We discuss the calculation process of optimal value, for example, proportional coefficient gain k nFC of fuzzy PID-controller using KB (KB1 and KB2) of two FC that designed for different control situations. Other coefficient gains are calculated with similar ways. A. Superposition state. Figure 11 shows 16 possible classical states in superposition that describe different correlation combinations (different type and class) between corresponding coefficient gains of two fuzzy PID-controllers. These two fuzzy PID-controllers are designed for different control situations. Figure 16 shows the example of k^FC calculation on possible set {kFC 1, kFC2, kFC 1, kFC2} , where kFC1is the designed (in off-line) control signal value of proportional coefficient gain of fuzzy PID-controller for first control situation; kFC2is the designed (in off-line) control signal value of differential coefficient gain of fuzzy PID-controller for second control situation (that essentially differ [on external functionality conditions of control object] from first situation). Using tensor product between Hadamard’s transform new combinations as kFC1® kFC2is received. Other combinations are received in similar ways. Design process of new robust coefficient gains of PID-controller using superposition state in on-line have many peculiarities. 1. In this case superposition as quantum state help us logically joint different KB and introduce priority at correlation of any states in superposition using different optimal criteria. Design of KB based on SCO (soft computing technology) realized by genetic algorithm (GA) that is random search on fixed possible solution space. In this case the random search of three coefficient gains {kp,kD,k,} in designed fuzzy PID-controller is independent for these coefficients and coordination control between them is absent. Its means that possible search other combination of coefficient gain schedules that have similar control effect (force control). 2. New types and classes of quantum correlations can realize coordination control of coefficient gains using only physical source of applied type and class of correlation. In this case new type and class of correlation can compress and reduce redundant information in independent control laws of coefficient gains, and as result extract more value information from responses of fuzzy PID-controllers on new unpredicted control situations. Therefore, this process designs new KB of FC in on-line with required level of robustness using new types of coordination control and quantum correlations. Application of entanglement in these three types of correlations gives new possibilities for increasing of KB-robustness based on new physical phenomena as teleportation between quantum states in designed superposition. This approach does not have classical analogies and characterize pure quantum nature of designed effect in intelligent control. 3. Selection of priority quantum state with fixed (in this case spatial) type of correlation is realized in Box V (see, Fig. 5) based on the definition of «Intelligent quantum state». B. Intelligent quantum state. Let us consider one of possible approach to optimal criteria choice of priority state extraction from designed superposition (Box IV, Fig. 8.2) of possible coding states for coefficient gains of fuzzy PID-controller. For this goal we are used the definition of «intelligent quantum state» [37] as the state with minimal uncertainty (minimum in Heisenberg inequality uncertainty). This definition is correlated with solutions of quantum wave equations (Schrödinger-like etc) when wave function of quantum system is described coherent state and uncertainty elation have global minimum. Definition and computation of intelligent state in QA are described in [37] using the definition of von Neumann entropy and Shannon information entropy in this quantum state. According to the definition [37] «intelligent quantum state» is the minimum of difference between Shannon information entropy and physical entropy von Neumann on this quantum state: Л (| Quantum state)) = min(HSh - Sv), (6) where H Sh and SvN are Shannon and von Neumann entropies, correspondingly. According to quantum information law we have the following inequality: HSh > SvN i.e., I(| Quantum state)) > 0 . Remark. In quantum mechanics according to Born’s rule probability p of quantum system state equal to amplitude probability ^ in degree 2: p = ^|2 that strong discussed last time in physics [38]. From quantum information viewpoint pure quantum state have zero value of von Neumann entropy. Thus «intelligent quantum state» (8.15) in QA corresponds to minimum of Shannon information entropy of quantum state. This minimum is achieved for maximum probability state (according to definition of Shannon information entropy HSh =-^pt Inpt , i.e., global minimum observed for maximum probabil-i ity Pt ). While p = ^|2, i.e., amplitude probability in degree 2, thus principle of amplitude probability maximum at correlated state can be used as priority selection criteria of «intelligent» correlated (coherent) state in superposition of possible candidates. Therefore, quantum oracle model is realized with calculation of amplitude probabilities in superposition state with mixed types of quantum correlations (Box V, Fig. 58.27) and selection state with maximum amplitude probability. According to definition, quantum oracle has full necessary information about solution. This algorithm is described in Figure 12. Extraction of this information (as analog of interference) is realized together of decoding operation. In our case decoding operation is standard procedure (inner product in Hilbert space) and described in Figure 14. With selection scaleable coefficient of designed output coefficient gains is realized iteration work of QFI. The developed QA-model for QFI can solve classical problems of robust KB design for FC in structures of ICS that does not have analogs of solutions in classical random algorithm’s families. This algorithm have polynomial computing complexity (BQP -class of computation complexity). C. Information transfer and communication in self-organization process. Let us consider the communication process between two KBs as communication between two players A and B, and let d = 2n. Ac- Электронный журнал «Системный анализ в науке и образовании» Выпуск №3, 2014 год cording to the law of quantum mechanics, initially we must prepare a quantum state description by density matrix p from two classical states (KB1 and KB2). The initial state p is shared between subsystems held by A (KB1) and B (KB2), with respective dimensions d, 1 d-1 1 p=^ SS(I W ®l <X'I) A ®(Ui*) B • 2 d k=0t=0 Here Uo = I and Ux changes the computational basis to a conjugate basis: |(ijujk^| = 1/dd V i, k . In this case, B chooses k randomly from d states in two possible random bases, while A has complete knowledge on his state. The state p can arise from the following scenario. A picks a random n-bit string k and sends B |k) or H®n | k) depending on whether the random bit t =0 or 1. Here H is the Hadamard transform. A can send t to B to unlock the correlation later. Experimentally, the Hadamard transform and measurement on single qubits are sufficient to prepare small, I(l) (p) = “logd • the state p and later extract the unlocked correlation in p . The initial correlation is The final amount of information after the complete measurement M in one-way communication is as [26] I a (p') = IC-)(p) = logd + 1, i.e., the amount of accessible extracted information increase. This phenomenon is impossible classically. However, states exhibiting this behaviour need not be entangled and corresponding communication can be organized using Hadamard’s transform [26]. Therefore, using the Hadamard transformation and a quantum correlation as communication between a few KB’s it is possible to increase initial information by quantum correlation. Structure of self-organized intelligent control system based on QFI model Let us consider the peculiarities of application the developed quantum control algorithm of selforganization to structures of self-organized intelligent control systems. Figure 15 show two equivalent structures of robust intelligent control system based on QFI model. In particular, Figure 15, a show the design process of robust KB based on QFI and quantum soft computing technology. For two different (fixed) control situations with SCO using new type of global intelligent feedback are prepared in off-line tuning corresponding two KB for FC1 and FC2. Unpredicted control situations (new reference signal, delay time in sensor system, noises in sensor system, in parameters and excitation on control object, etc) reflect new control error (see, Fig. 15, a). Let us consider the peculiarities of control system structure that is presented in Fig. 15. - Responses of these two FC1(2) are new control signals of coefficient gains for fuzzy PID-controllers. - These control signals are inputs to QFI that in parallel are prepared in superposition state (see, Figs 7 and 11). - Output of QFI is a new control signal for coefficient gains of PID-controller. - Thus two FC1(2) together with QFI organize in on-line tuning the structure of QFC (see, Fig. 16, a). - Figure 16, b show how the structure of intelligent control system based on QFC is realized the selforganization principle based on QFI model and supports the thermodynamic trade-off. - Template of initial states is organized from current control signals as response on a new control error from unpredicted control situation. - Self-assembly of control signals is realized with superposition and selection of new quantum correlation in superposition of corresponding signals. - Extraction of value hidden information is realized in QFI with corresponding quantum operators as quantum oracle and interference that increases the information amount for decision making according (6). - As result new robust self-organized KB is designed. (a) (b) Figure 16. Two equivalent structures of self-organized intelligent control system Q: What is a difference between our approach and Natural (or man-made) models of selforganization? A: Main differences are as followings. 1. In our approach a self-organization process is described as a logical process of value information extraction from hidden layers (possibilities) in classical control laws using quantum logic of QFI-models based on main facts of QC and QAs theories; 2. Structure of QFI is includes all of natural elements of self-organization (templating, self-assembly, and self-organization structure) with corresponding quantum operators (superposition of initial states, selection of quantum correlation types and classes, quantum oracles, interference, and measurements). 3. QFI is quantum search algorithm (belonging to QPB-class) that can solve classical algorithmic unsolved problems. 4. In QFI the self-organization principle is realized using the on-line responses in a dynamic behavior of classical FCs on new control errors in unpredicted control situations for the design of robust intelligent control; 5. Model of QFI supports the thermodynamic interrelations between stability, controllability and robustness for design of self-organization processes. Let us consider concrete example of practical application of QFI to robust KB design of fuzzy PID-controllers. Robust KB design of fuzzy PID-controllers: Application of QFI In this section we are briefly describe the application of QFI to design of robust KB of fuzzy PID-controller for intelligent control system of essentially non-linear control object. Example: Robust intelligent control of non-linear control objects (with essential dissipation and local unstable). Equation of motion and designed control force are described together with thermodynamic constraint as following: x + [ 2в + ax2 + kxx2 -1] x + kx = £( t) + u (t); ^x- = ^2p + ax2 + kxx2 - 1J x • x, where £(t) describes random excitations with fixed probability density functions; u(t) is designed optimal control force; S and x are entropy production and entropy production rate, correspondingly. x dt If in Eq. (8) we have condition as: 2в + ax2 + kxx2< 1 then entropy production rate is non-positive, i.e., ^x< 0 and the system (8) has local time-dependent unstable states. Figure 17 show the thermodynamic interpretation of local unstable states in (8). Remark. Negative entropy production for local unstable states in oscillatory processes was also described in [39]. The system (8) has different dynamic behavior if parameters of structure are changing: for в = 0.5 (other parameters are for example, a = 0.3;kx = 0.2;k = 5) the system (8.17) is asymptotically stable; for в = -1 (other parameters are same as before) the system is local unstable and has auto-vibration cycles. Dynamic phase portrait of the system (8) has strange attractor. Thus for small vibrations the system (8) is local unstable and it is design problem of robust control for reference signal x = 0 and small random vibrations of control object. Figure 17. Thermodynamic interpretation of local unstable states in (8) А. Let us consider off-line tuning of FC in learning situations. Learning situation of KB-design for FC1. Initial parameters of (8) are в = 0.5;a = 0.3;kx = 0.2;k = 5 and initial conditions are x0; x0= 2.5; 0.1; reference signal xref = 0; coefficient gain are simulated in the range [0, 10]; external random excitation is random process with Raleigh probability density function. This control situation is defined as teaching situation TS1. Learning situation of KB-design for FC2. Initial parameters of (8) are в = -1; a = 0.3; kx = 0.2; k = 5 and initial conditions are x0; x0= 2.5; 0.1; reference signal xref = -1; coefficient gain are simulated in the range [0,10]; external random excitation is random process with Raleigh probability density function (same as in TS1). This control situation is defined as teaching situation TS2. B. Control problem: (i) transfer control object from initial state x, x= 2.5, 0.1 in final state (reference signal) in present of random noises on control object, changing of parameters in structure of control object and control goals (reference signals); (ii) estimate sensitivity and level of robustness of designed FC1(2) in comparison with traditional PID-controller and self-organized FC with KB designed on basis of QFI in unpredicted control situation. Figure 17,a show simulation results of control in situation TS2 using structure in Fig. 16. In this case TS2 is unpredicted control situation for FC1 (essentially are changing parameters of control object structure and reference signal). Figure 18,b shows main performance and principle of self-organization process that is described in Figure 18,a. C. Analysis of simulation results and physical interpretation of self-organization process in QFC in unpredicted control situation. Figure 8.17,a shows that in transient process (temporal period interval [0, 1.5 sec]) self-organized QFC is used trajectory of traditional PID-controller with smaller integral coefficient gain. Fi gure 19 shows values of generalized entropies in system «control object + FC» according to Eq. (8). In this case entropy production in control object and in QFC is decreased. Figure 18. Simulation results of intelligent control for fixed control situation TS2 Figure 19. Temporal behavior of generalized entropies In this case we have necessary equilibrium between qualitative and quantitative characteristics of Lyapunov stability, controllability, and robustness of control processes: minimum of generalized entropy guarantee robustness stability and controllability of (8). As mentioned above in this case FC2 was tuning in TS2 and for FC1 this situation is unpredicted control situation. QFC is used coordination control between correspond control signals based on quantum correlation in QFI and Eq. (8). Using this effect self-organized QFC can extract the value information from transient process of FC2 and response of FC1 on unpredicted control situation: QFC is used in control laws of coefficient gains the information about optimal time re-26 Электронный журнал «Системный анализ в науке и образовании» Выпуск №3, 2014 год sponse (smart solution) of FC2 in TS2 (see, Figure 18, a) and then after self-learning begin organize selfadaptation (see, Fig. 18, b) using the performance of non-periodical process of FC1 (without transient process). It is important that itself FC1 do not achieve the control goal (see, Fig. 18, b), and FC2 is used transient process and has local unstable states (see, Fig. 19). Therefore, to achieve the control goal (reference signal as -1) in self-organized QFC is realized selflearning process, extraction of value information for design wise control signal of coefficient gains from response of two FC1(2) on unpredicted control situation and then is used adaptation in real time. Quantum (unlocked) hidden correlation is used in self-organized QFC for design of coordination control between coefficient gains in fuzzy PID-controller. In our case quantum correlation includes the information about current values of coefficient gains and self-organized QFC is used for achievement of control goal the performance of optimal time control of FC2 and non-transient (aperiodical) behavior of FC1. As result high quality and performance of intelligent control is achieved. Remark. In above discussed example the effect of value information extraction for self-organized QFC with QFI was achieved in situation when FC2 is used in learning situation TS2. So we consider the robustness of intelligent control system on learning situations when one of situation TS2 was considered as unpredicted control situation for FC1 that tuning on TS1 (for TS1 was changing essentially parameter в in control object structure and reference signal). It is the paradox (from advanced control viewpoint) that with FC1 (that do not achieve the control goal) and FC2 (that have transient process and local unstable) the selforganized QFC can achieve the control goal using information from responses of both controllers FC1(2). Q: This effect is saved in more general (than learning situations) unpredicted control situations? Let us below given the positive answer on this important for intelligent control question. Example: Robustness of self-organized QFC in unpredicted control situation. For the answer on this question we will consider more complex unpredicted (for both FC1 and FC2) control situation. For new unpredicted control situation we have prepared following new parameters: (i) reference signal xref = 0 ; (ii) Raleigh external noise; (iii) new parameter в = - 0.1 in control object; (iv) constraint on control force u< |10| [N]; (v) in measurement system is introduced Gaussian noise with coefficient gain 0.02; (vi) time delay of control error signal 0.0125 sec. Other parameters are similar as in above example. Thus unpredicted control situation is characterized with new noises in measurement system, time delay of current control error information for FC1 and FC2, and jump changing of structure parameter in control object. Figure 20 shows results of simulation using structure of intelligent system in Figure 16. '10 20 40 60 80 100 120 140 160 180 200 '^O 20 40 60 80 100 120 140 160 180 200 Time (S) (a) (b) Figure 20. Results of dynamic behavior (a) of control object; and (b) control error Control laws of coefficient gains and integral control error are shown in Figure 21. Fig. 22 shows the loss of resource of intelligent control system as increases of generalized entropy productions in the system as general object: «control object + fuzzy PID-controller». The results of simulations are shown that both FC1 and FC2 do not achieved the control goal and have increased loss of resources. QFC can extract the important information from responses of these FCs and control object, and achieve the control goal with minimum of entropy production. New unpredicted control situation: new type of Rayleigh noise; new sensor delay time = 0.0125;sensor noise in measurement; new model parameters: beta = - 0.1 Figure 21. Results of simulation of integral error and control laws of coefficient gains Figure 22. Temporal behavior of generalized entropies of FC1, FC2 and QFC It’s means that in this case self-organization in QFC supports the thermodynamic trade-off between stability, controllability, and robustness in control object behavior (8). Therefore, the effect of self-organization in QFC is saved for complex unpredicted situation. The simulation results show also that from two non robust FC1(2) with using of quantum control strategies it is possible to design universal robust QFC with simple control laws of coefficient gain schedules of fuzzy PID-controller. Therefore, according to Figure 18 self-organization process can be separated in this case on two complementary parts: self-learning (in transient process) and self-adaptation that increase the level of robustness of intelligent control systems in on-line. Similar effect was described in [22 – 25]. The discussed examples are illustrated the effectiveness of quantum approach to design of wise robust intelligent control and for solving with quantum soft computing classical algorithmic unsolved problems on classical level based on the methodology [27, 28, 40 - 46]. Conclusions SCO allows us to model different versions of KBs (multiple-KB) of FC that guarantee robustness for fixed control environments. 1. Self-organization principle in quantum FC with minimum entropy in intelligent control states in on-line regime is introduced. 2. The QFI block enhances robustness of FC using a self-organizing capability. 3. Designed quantum FC achieves the prescribed control objectives in many unpredicted control situations: The reliability of intelligent control system based on QFI is increased in unpredicted control situations. 4. Using SCO and QFI we can design wise control of essentially non-linear stable and, especially, of unstable dynamic systems in the presence of information uncertainty about external excitations and of changing reference signals (control goal), and model parameters. 5. Control laws based on QFI are simple for the physical realization. 6. QFI based FC (QFC) requires minimum of the initial information about external environments and internal structure of control object model. 7. On-line process for extraction of the value information for wise control and in design of the unified robust KB in quantum FC is used.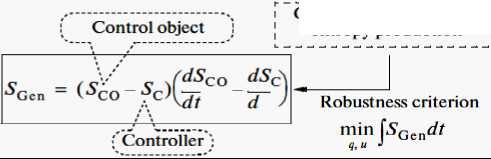



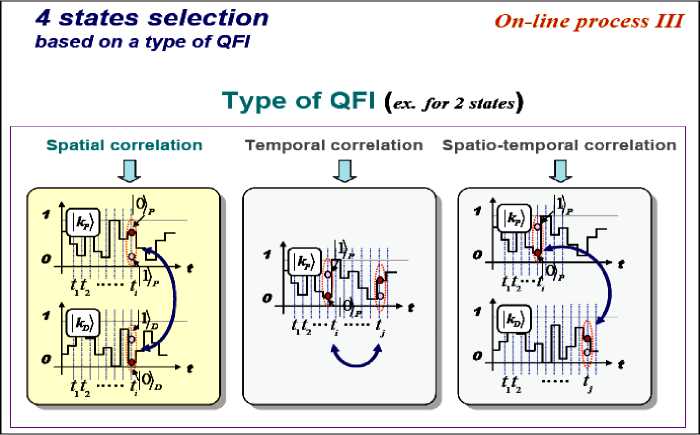
P
® k FC2
® k FCl
® k FC C


Список литературы Quantum fuzzy inference model as quantum control algorithm of self-organization (minimum entropy principle relative to quantum knowledge)
- Ulyanov S.V. Self-organized control system: US patent, №. 6, 411, 944, 1997; see also Self-organization fuzzy chaos intelligent controller for robotic unicycle: A new benchmark in AI control // Proceedings 5th Intelligent System Symposium, Tokyo, Sep. 29 -30, 1995. - Pp.41-46.
- Ulyanov S.V., Litvintseva L.V., Ulyanov I.S., Ulyanov S.S. Quantum information and quantum computational intelligence: Quantum optimal control and filtering - Stability, robustness, and self-organization models in nanotechnologies // Note del Polo Ricerca, Università degli Studi di Milano. - Milan, 2005. -Vol. 82.
- Ulyanov S.V., Litvintseva L.V., Ulyanov S.S. Quantum swarm model of self-organization process based on quantum fuzzy inference and robust wise control design // Proc. 7th International Conference on Application of Fuzzy Systems and Soft Computing (ICAFS'2006), September 13-14, 2006. - Siegen, Germany, 2006. - Pp. 10-19.
- Camazine S., Deneubourg J.-L., Franks N.R., Sneyd J., Theraulaz G., Bonabeau E. Self-organization in biological systems. - Princeton University Press, 2008.
- Hemelrijk C.K. (Ed.) Self-organisation and evolution of social systems. - UK: Cambridge University Press, 2005.


