Quantum software engineering. Pt II: quantum computing supremacy on quantum gate-based algorithm models

Ulyanov S., Tyatyushkina O., Korenkov V. Quantum software engineering Pt II: Quantum computing supremacy on quantum gate-based algorithm models. System Analysis in Science and Education, 2021;(1):81– 129. Available from:

There are several known quantum algorithms that offer various advantages or speedups over classical computing approaches, some of them even reducing the complexity class of the problem. These algorithms generally proceed by controlling the quantum interference between the components of the underlying entangled superpositions in such a way that only one or relatively few quantum states have a significant amplitude in the end. A subsequent measurement can therefore provide global information on a massive superposition state with significant probability. The coherent manipulation of quantum states that defines a quantum algorithm can be expressed through different quantum computational modes with varying degrees of tunability and control. The most powerful quantum computing mode presently known is the universal gate model, similar to universal gate models of classical computation. Here, a quantum algorithm is broken down to a sequence of modular quantum operations or gates between individual qubits. There are many universal quantum gate families operating on single and pairwise qubits, akin to the NAND gate family in classical computing. One popular universal quantum gate family is the grouping of two-qubit CNOT gates on every pair of qubits along with rotation gates on every single. With universal gates, an arbitrary entangled state and thus any quantum algorithm can be expressed. Alternative modes such as measurement-based or cluster-state quantum computing can be shown to be formally equivalent to the universal gate model. Like the NAND gate in the classical CMOS technology, the particular choice of a universal gate set or even a mode of quantum computing is best determined by the quantum hardware itself and its native interactions and available controls. The structure of the algorithm itself may also impact the optimal choice of gate set or quantum computing mode.

The difference between classical and quantum algorithms (QA)s is following: problem solved by QA is coded in the structure of the quantum operators. Input to QA in this case is always the same. Output of QA says which problem was coded. In some sense, you give a function to QA to analyze and QA returns its property as an answer without quantitative computing. QA studies directly qualitative properties of the functions. The core of any QA is a set of unitary quantum operators in matrix form or corresponding structure of quantum gates. In practical representation, a quantum gate is a unitary matrix with a particular structure. The size of this matrix grows exponentially with the number of inputs, making it impossible to simulate QAs with more than 30-35 inputs on a classical computer with von Neumann architecture. Background of quantum computing is matrix calculus. New quantum gate-based algorithms and new algorithmic paradigms

(such as adiabatic computing which is the quantum counterpart of simulated annealing) have been discovered. We can explore several aspects of the adiabatic quantum computational model and use a way that directly maps any arbitrary circuit in the standard quantum computing models to an adiabatic algorithm of the same depth. Many quantum algorithms developed for the so-called oracle model in which the input is give as an oracle so that the only knowledge we can gain about the input is in asking queries to the oracle. As our measure of complexity, we use the query complexity. The query complexity of an algorithm A computing a function F is the number of queries used by A . The query complexity of F is the minimum query complexity of any algorithm computing F .

We are interested in proving lower bounds of the query complexity of specific functions and consider methods of computing such lower bounds. The two most successful methods for proving lower bounds on quantum computations are as follows: the adversary method and the polynomial method. An alternative measure of complexity would be to use the time (temporal) complexity that counts the number of basic operations used by an algorithm. The temporal complexity is always at least as large as the query complexity since each query takes one-unit step, and thus a lower bound on the query complexity is a lower bound on the temporal complexity. For most existing quantum algorithms, the temporal complexity is within poly-logarithmic factors of the query complexity.

One barrier to better understanding of the quantum query model is the lack of simple mathematical representations of quantum computing models. While classical query complexity (both deterministic and randomized) has a natural intuitive description in terms of decision trees, there is no such easy description of quantum query complexity. The main difference between the classical and quantum case is that classical computations branch into non-interacting sub computations (as represented by the tree) while in quantum computations, because of the possibility of destructive interference between sub-computations, there is no obvious analog of branching. The bounded-error model is both relevant to understanding powerful explicit non-query quantum algorithms (such as Shor’s factoring algorithm) and theoretically important as the quantum analogue of the classical decision tree model.

There are other modes of quantum computation that are not universal, involving subsets of universal gate operations, or certain global gate operations with less control over the entire space of quantum states. These can be useful for specific routines or quantum simulations that may not demand full universality. Although global adiabatic Hamiltonian quantum computing can be made universal in certain cases, it is often better implemented as non-universal subroutines for specific state preparation. Quantum annealing models do not appear to be universal, and there is current debate over the advantage such models can have over classical computation. Gates that explicitly include error, or decoherence processes, used to model quantum computer systems interacting with an environment via quantum simulation.

Main Quantum Computing Circuits and Gate-based Devices Platform

The fundamental concepts required for designing and operating quantum computing devices by reviewing state of the art efforts to fabricate and demonstrate quantum gates and qubits demonstrated [1-23].

The development of quantum computing technologies builds on the unique features of quantum physics while borrowing familiar principles from the design of conventional devices. The near-term challenges for devices based on semiconducting, superconducting, and trapped ion technologies with an emphasis on design tools as well as methods of verification and validation summarized. The generation and synthesis of quantum circuits for higher-order logic that can be carried out using quantum computing devices discussed. While the tutorial captures many of the introductory topics needed to understand the design and testing of quantum devices, several more advanced topics have been omitted due to space constraints. Foremost is the broader theory of quantum computation, which has developed rapidly from early models of quantum Turing machines to a number of different but equally powerful computational models. In addition, we have largely omitted the sophisticated techniques employed to mitigate the occurrence of errors in quantum devices. Quantum error correction is an important aspect of long-term and large-scale quantum computing, which uses redundancy to overcome the loss in information from noisy environments. Finally, the review of quantum computing technologies is intentionally narrowed to three of the leading candidates for large-scale quantum computing. However, there is a great diversity of experimental quantum physical systems that can be used for encoding and processing quantum information. Quantum computing promises new capabilities for processing information and performing computationally hard tasks. This includes significant algorithmic advances for solving hard problems in computing, sensing, and communication. The breakthrough examples of Shor’s algorithm for factoring numbers and Grover’s algorithms for unstructured search have fueled a series of more recent advances in computational chemistry, nuclear physics, and optimization research among many others. However, realizing the algorithmic advantages of quantum computing requires hardware devices capable of encoding quantum information, performing quantum logic, and carrying out sequences of complex calculations based on quantum mechanics.

For more than 35 years, there has been a broad array of experimental efforts to build quantum computing devices to demonstrate these new ideas. Multiple state-of-the-art engineering efforts have now fabricated functioning quantum processing units (QPUs) capable of carrying out small-scale demonstrations of quantum computing. The QPUs developed by the commercial vendors such as IBM, Google, D-Wave, Rigetti, and IonQ are among a growing list of devices that have demonstrated the fundamental elements required for quantum computing. This progress in prototype QPUs has opened up new discussions about how to best utilize these nascent devices.

Quantum computing poses several new challenges to the concepts of design and testing that are unfamiliar to conventional CMOS-based computing devices.

For example, a striking fundamental challenge is the inability to interrogate the instantaneous quantum state of these new devices. Such interrogations may be impractically complex within the context of conventional computing, but they are physically impossible within the context of quantum computing due to the nocloning principles. This physical distinction fundamentally changes the understanding how QPUs are designed and their operation tested relative to past practice. This tutorial provides an overview of the principles of operation behind quantum computing devices as well as a summary of the state of the art in QPU.

The continuing development of quantum computing will require expertise form the conventional design and testing community to ensure the integration of these non-traditional devices into existing design workflows and testing infrastructure. There is a wide variety of technologies under consideration for device development, and this tutorial focuses on the current workflows surrounding quantum devices fabricated in semiconducting, superconducting, and trapped ion technologies. We also discuss the design of logical circuits that quantum devices must execute to perform computational work.

Principles of Quantum Computing

The principles of quantum computing derive from quantum mechanics, a theoretical framework that has accurately modeled the microscopic world for more than 100 years. Quantum computing draws its breakthroughs in computational capabilities from the many unconventional features inherent to quantum mechanics, and we provide a brief overview of these features while others offer more exhaustive explanations. In quantum mechanics, all knowable information about a physical system is represented by a quantum state. The quantum state is defined as vector within a Hilbert space, which is a complex-valued vector space supporting an inner product. By convention, the quantum state with label Ψ is expressed as a column vector using the “ket” notation as ψ , while the dual vector is expressed as the row vector ”bra” ψ . The inner product between these two vectors is ψψ and normalized to one. An orthonormal basis for an N-dimensional Hilbert space satisfies ij = δ , and an arbitrary quantum state may be represented within a

N - 1

complete basis as ψ = ∑ cj . Given the continuous amplitudes that define their quantum states ψ , j = 0

quantum computers have characteristics akin to classical analog computers, where errors can accumulate over time and lead to computational instability. It is thus critical that quantum computers exploit the technique of quantum error correction (QEC), or at least have sufficiently small native errors that allow the system to complete the algorithm. QEC is an extension of classical error correction, where ancilla qubits are added to the system and encoded in certain ways to stabilize a computation through the measurement of a subset of qubits that is fed back to the remaining computational qubits. There are many forms of QEC, but the most remarkable result is the existence of fault-tolerant QEC, allowing arbitrarily long quantum computations with sub-exponential overhead in the number of required additional qubits and gate operations. Qubit systems typically have native noise properties that are neither symmetric nor static, so matching QEC methods to specific qubit hardware noise profiles will play a crucial role in the successful deployment of quantum computers. The general requirements for quantum computer hardware are that the physical qubits (or equiva- lent quantum information carriers) must support (i) coherent Hamiltonian control with sufficient gate expression and fidelity for the application at hand, and (ii) highly efficient initialization and measurement.

These seemingly conflicting requirements limit the available physical hardware candidates to just a few at this time. Below we describe those platforms that are currently being built into multi-qubit quantum computer systems and are expected to have the largest impact in the next decade. As we will see below in a definition of levels of the quantum computer stack and a sampling of vertical implementations and applications, the near-term advances in quantum computer science and technology will rely on algorithm designers understanding the intricacies of the quantum hardware, and quantum computer builders understanding the natural structure of algorithms and applications.

Quantum Algorithms. Practical interest in quantum computing arose from the discovery that there are certain computational problems that can be solved more efficiently on a quantum computer than on a classical computer, notably number factoring (Shor’s algorithm) and searching unstructured data (Grover’s algorithm). Quantum algorithms typically start at a very high level of description, often as pseudo code. These algorithms are usually distinguished at this level of abstraction by very coarse scaling of resources such as time and number of qubits, as well as success metrics, such as success probabilities or the distance between a solution and the optimal value. Quantum algorithms can be broadly divided into those with provable success guarantees and those that have no such proofs and must be run with heuristic characterizations of success. Once a quantum algorithm has been conceptualized with the promise of outperforming a classical algorithm, it is common to consider whether the algorithm can be run on near-term devices or for future architectures that rely on quantum error correction. A central challenge for the entire field is to determine whether algorithms on current, relatively small quantum processors can outperform classical computers, a goal called quantum advantage. For fault-tolerant quantum algorithms on the other hand, there is a larger focus on improving the asymptotic performance of the algorithm in the limit of large numbers qubits and gates. Shor's factoring and Grover's unstructured search algorithms are the examples of “textbook” quantum algorithms with provable performance guarantees. A handy guide to known quantum algorithms is the quantum algorithm zoo, Another important example is the HHL algorithm which is a primitive for solving systems of linear equations. Factoring, unstructured search, and HHL are generally thought to be relevant only for larger fault-tolerant quantum computers.

Another class of quantum algorithm are quantum simulations, which use a quantum computer to simulate models of a candidate physical system of interest, such as molecules, materials, or quantum field theories whose models are intractable using classical computers. Quantum simulators often determine physical properties of a system such as energy levels, phase diagrams, or thermalization times, and can explore both static and dynamic behavior. There is a continuum of quantum simulator types, sorted generally by their degree of system control. Fully universal simulators have arbitrary tunability of the interaction graph and may even be fault-tolerant, allowing the scaling to various versions of the same class of problems. Some quantum simulations do not require the full universal programmability of a quantum computer, and are thus easier to realize. Such quantum simulators will likely have the most significant impact on society in the short run. Example simulator algorithms range from molecular structure calculations applied to drug design and delivery or energy-efficient production of fertilizers, to new types of models of materials for improving batteries or solar cells well beyond what is accessible with classical computers.

Variational quantum algorithms such as the variational quantum eigensolver (VQE) and the quantum approximate optimization algorithm (QAOA) are recent developments. Here, the quantum computer produces a complex entangled quantum state representing the answer to some problem, for example, the ground state of a Hamiltonian model of a material. The procedure for generating the quantum state is characterized by a set of classical control parameters that are varied in order to optimize an objective function such as minimizing the energy of the state. One particular area of active exploration is the use of VQE or QAOA for tasks in machine learning or combinatorial optimization, as discussed below. Variational quantum solvers are a workhorse in near-term quantum hardware, partly because they can be relatively insensitive to systematic gate errors. However, these algorithms are usually heuristic: one cannot generally prove that they converge. Instead, they must be tested on real quantum hardware to study and validate their performance and compare to the best classical approaches.

Quantum algorithms are typically expressed at a high level with the need to estimate actual resources for implementation. This often starts with a resource estimate for fault-tolerant error-corrected quantum computers, where the quantum information is encoded into highly entangled states with additional qubits in order to protect the system from noise. Fault-tolerant quantum computing is a method for reliably processing this encoded information even when physical gates and qubit measurements are imperfect. The catch is that quantum error correction has a high overhead cost in the number of required additional qubits and gates. How high a cost depends on both the quality of the hardware and the algorithm under study. A recent estimate is that running Shor’s algorithm to factor a 2048-bit number using gates with a 10 - 3 error rate could be achieved with currently known methods using 20 million physical qubits. As the hardware improves, the overhead cost of fault-tolerant processing will drop significantly; nevertheless, fully fault-tolerant scalable quantum computing is presently a distant goal. When estimating resources for fault-tolerant implementations of quantum algorithms, a discrete set of available quantum gates is assumed, which derive from the details of the particular error-correcting code used. There are many different techniques for trading off space (qubit number) for time (circuit depth), resembling conventional computer architecture challenges. It is expected that optimal error correction encoding will depend critically upon specific attributes of the underlying quantum computing architecture, such as qubit coherence, quantum gate fidelity, and qubit connectivity and parallelism.

Estimating resources for quantum algorithms using realistic quantum computing architectures is an important near-term challenge. Here, the focus is generally on reducing the gate count and quantum circuit depth to avoid errors from qubit decoherence or slow drifts in the qubit control system. Different types of quantum hardware support different gate set and connectivity, and native operations are often more flexible than fault-tolerant gate sets for certain algorithms. This optimizing of specific algorithms to specific hardware is the highest and most important level of quantum computer co-design.

Conventional Quantum Algorithms

Historically, Shor's and Grover's algorithms, which are sometimes referred to as “textbook algorithms,” were the first algorithms of practical relevance where a quantum computer offered a dramatic speedup over the best-known classical approaches. Here we consider co-design problems and full-stack development opportunities that arise from mapping these textbook algorithms to quantum computing platforms. At the top of the stack, the challenges that both algorithms face include implementing classical oracles with quantum gates. In Grover's algorithm, the oracle can be implemented using Bennett’s pebbling game. However, it is a non-trivial task to find an efficient reversible circuit, since the most efficient implementation on a quantum computer may not follow the structure suggested by a given classical algorithmic description, even when latter is efficient. There are also intriguing questions in terms of how we can use classical resources to aid in quantum algorithms. For example, in Shor's algorithm we can leverage classical optimizations such as windowed arithmetic, or trade off quantum circuit complexity with classical post-processing complexity. One of the key challenges in implementing textbook algorithms in physical systems is to optimize these algorithms for a given qubit connectivity and native gate set. While these technology-dependent factors will not affect asymptotic scaling, they could greatly influence whether these algorithms can be implemented on near-term devices. For instance, high connectivity between qubits can provide significant advantages in algorithm implementation. Also, in this vein, the work has been done to implement Shor's algorithm with a constrained geometry (1D nearest neighbor), but there are many open questions that involve collaborations across the stack.

Developing implementations of Shor's algorithm and Grover's algorithm will provide exciting avenues for improved error correction, detection, and mitigation. While error correction codes are often designed to correct specific types of errors for particular physical systems, considering error correction for textbook algorithms provides a basis for designing error correction for both application and hardware. Because the output of these textbook algorithms are easily verifiable, they are good testbeds for error mitigation and characterization. For example, simple error correction/mitigation circuits, including randomized compiling, could be implemented in the context of small implementations of Grover’s algorithm and Shor’s algorithm to better understand the challenges in integrating these protocols into more complex ones. While this approach has been used in the quantum annealing community, it could be fruitful to explore in more detail for textbook gate-based algorithms.

Grover’s algorithm seems to break down in the presence of a particular type of error that appears to be unrealistic in actual physical systems. For other algorithms, realistic errors do not appear to be as detrimental. Testing textbook algorithms on different architectures with and without error mitigation would provide us with a way to explore the space of errors relative to a specific algorithm, and give insight into which realistic errors are critical. This would inform error mitigation (not necessarily correction) techniques at both the code and hardware level, tailored to specific algorithms. This way of viewing error correction calls for a full integration of experts at the hardware, software, and algorithm design levels. The work on these textbook algorithms will lead to improved modularity in the quantum computing stack. In software design, modularity refers to the idea of decomposing a large program into smaller functional units that are independent and whose implementations can be interchanged. Modular design is a scalable technique that allows the development of complex algorithms while focusing on small modules, each containing a specific and well isolated functionality. These modules can exist both at the software level as well as at the hardware level. As an example, in classical computing, the increased use of machine learning algorithms and cryptocurrency mining has led to a repurposing of GPUs. In the design of full implementations of quantum algorithms such as Shor’s and Grover’s, modular design can be applied by using library functions that encapsulate circuits for which an optimized implementation was derived earlier. The examples include quantum Fourier transforms, multiple-control gates, libraries for integer arithmetic and finite fields, and many domain-specific applications such as chemistry, optimization, and finance. All major quantum computing programming languages are open source, including Googles Cirq, IBMs QisKit, Microsofts Quantum Development Kit, and Rigettis Quil, which facilitates the development and contribution of such libraries. Highly optimized libraries that are adapted to specific target architectures as well as compilers that can leverage such libraries and further optimize code are great opportunities for large-scale collaborative efforts between academia, industry, and national labs. Like libraries, programming patterns provide opportunities for modularity. Programming patterns capture a recur-ring quantum circuit design solution that is applicable in a broad range of situations. Typically, a pattern consists of a skeleton circuit with subroutines that can be instantiated independently. The examples of patterns are various forms of Quantum Phase Estimation (QPE), amplitude amplification, period finding, hidden subgroup problems, hidden shift problems, and quantum walks.

Implementing textbook algorithms will become important benchmarks for the quantum computing stack as a whole and also at the level of individual components. The need for such benchmarks is evident in the recent proliferation of a variety of benchmarks that test various aspects and components of quantum systems and entire systems, such as quantum volume, two-qubit fidelity, cross-entropy, probability of success, reversible computing, and the active IEEE working group project. It is not likely that any single benchmark will characterize all relevant aspects of a quantum computer system. However, implementing textbook algorithms provides an easy-to-verify test of the full quantum system from hardware to software, as all the aspects of the system must work in concert to produce the desired output.

Quantum Software. A quantum computer will consist of hardware and software. The key components of the software stack include compilers, simulators, verifiers, and benchmarking protocols, as well as the operating system. Compilers - interpreted to include synthesizers, optimizers, transpilers, and the placement and scheduling of operations - play an important role in mapping abstract quantum algorithms onto efficient pulse sequences via a series of progressive decompositions from higher to lower levels of abstraction. The problem of optimal compilation is presently intractable suggesting an urgent need for improvement via sustained research and development. Since optimal synthesis cannot be guaranteed, heuristic approaches to quantum resource optimization (such as gate counts and depth of the quantum circuit) frequently become the only feasible option. Classical compilers cannot be easily applied in the quantum computing domain, so quantum compilers must generally be developed from scratch. Classical simulators are a very important component of the quantum computer stack. There are a range of approaches, from simulating partial or entire state vector evolution during the computation to full unitary simulation (including by the subgroups), with or without noise. Simulators are needed to verify quantum computations, model noise, develop and test quantum algorithms, prototype experiments, and establish computational evidence of a possible advantage of the given quantum computation. Classical simulators generally require exponential resources (otherwise the need for a quantum computer is obviated), and thus are only useful for simulating small quantum processors with less than 100 qubits, even using high-performance supercomputers. Simulators used to verify the equivalence of quantum circuits or test output samples of a given implementation of a quantum algorithm can be thought of as verifier. Benchmarking protocols are needed to test components as well as entire quantum computer systems. Quantum algorithm design, resource trade-os (space vs. gate count vs. depth vs connectivity vs. fidelity, etc.), hardware/software co-design, efficient architectures, and circuit complexity are the examples of the important areas of study that directly advance the power of software. The quantum operating system (QOS) is the core software that manages the critical resources for the quantum computer system. Similar to the OS for classical computers, the QOS will consist of a kernel that manages all hardware resources to ensure that the quantum computer hardware runs without critical errors, a task manager that prioritizes and executes user-provided programs using the hardware resources, and the peripheral manager that handles peripheral resources such as user/cloud and network interfaces. Given the nature of qubit control in near-term devices which requires careful calibration of the qubit properties and controller outputs, the kernel will consist of automated calibration procedures to ensure high fidelity logic gate operation is possible in the qubit system of choice.

Control Engineering. Advancing the control functions of most quantum computing implementations is largely considered an engineering and economic problem. Current implementations comprise racks of test equipment to drive the qubit gate operations, calibrate the qubit transitions and related control, and calibrate the measurement equipment. While appropriate for the early stages of R&D laboratory development, this configuration will limit scalability, systems integration and applicability for fielded applications and mobile platforms, and affordability and attractiveness for future applications. The quantum gate operations for most qubit technologies require precise synthesis of analog control pulses that implement the gates. These take the form of modulated electromagnetic waves at relevant carrier frequencies, which are typically in the microwave or optical domain. Depending on the architecture of the quantum computer, a very large number of such control channels might be necessary in a given system. While the advances in communication technologies can be leveraged, these have to be adapted for quantum applications. A significant level of flexibility and programmability to generate the required pulses with adequate fidelity must be designed into the control system for quantum computers. The advancement of controls in quantum computing will ultimately require high-speed and application-specific optimized controls and processing. This situation mirrors the explosive advancement of the telecommunications industry in its implementation of 100 to 400+ Gb/s coherent digital optics formats and integrated RF and microwave signal processing for mobile applications. In the short run, however, the challenge we face is defining the control functions and features relevant for the target qubit applications and deriving the required performance specifications. This work is necessary before a dedicated, integrated, and scalable implementation such as ASIC development becomes viable. Near-term applications in quantum computing and full system design activities are critical in identifying and defining these needs. There are strong opportunities to engage engineering communities - in academia, national laboratories, and industry - with expertise ranging from computer architecture to chip design to make substantial advances on this front. To foster such efforts, it will be necessary to encourage co-design approaches and to identify common engineering needs and standards. Generating the types of signals needed can benefit significantly from digital RF techniques that have seen dramatic advances in the last decade. We envision commercially available chipsets based on field-programmable gate arrays (FPGAs) and ASICs that incorporate “System on a Chip” (SoC) technology, where processing power is integrated with programmable digital circuits and analog input and output functions. Besides the signal generation necessary for implementing the gates, other control needs include passive and active (servo) stability, maintenance of system operation environment (vacuum, temperature, etc.), and managing the start-up, calibration, and operational sequences. Calibration and drift control are important to both atomic and superconducting systems, though in somewhat different ways. In fixed-frequency superconducting systems, maintaining fidelities above 99% requires periodic calibration of RF pulse amplitudes; for tunable transmons, low frequency tuning of magnetic flux is required to maintain operation at qubit sweet spots. For atomic qubits, calibrating local trapping potentials and slow drifts in laser intensities delivered to the qubits is necessary. These calibration procedures, which can be optimized, automated, and built into the operating mode of the quantum computer system with help of software controls, are the candidates for implementation in SoC technologies. The development of optimal operating procedures for drift control and calibration processes will require innovation at a higher level of the stack. For example, dynamically understanding how control parameter drifts can be tracked and compensated and when recalibration is needed (if not done on a fixed schedule) will require high-level integration.

Specific performance requirements will help drive progress, by co-design of engineering capabilities and quantum control needs. For example, there is a need for electronic control systems encompassing: (i) analog outputs with faster than 1G samples/s; (ii) synchronized and coherent output with over 100 channels and extensible to above 1000 channels; (iii) outputs switchable among multiple pre-determined states; and (iv) proportional-integrative-derivative (PID) feedback control on each channel with at least kHz bandwidth. Common needs for optical control systems include (i) phase and/or amplitude modulation with a bandwidth of ≈ 100 MHz; (ii) over 100 channels and extensibility to above 1000 channels; (iii) precision better than 12 bits (phase or amplitude); and (iv) operating wavelengths to match qubit splitting.

An essential consideration of the control engineering for high-performance quantum computers is noise. The noise in a quantum system has two distinct sources: one is the intrinsic noise in the qubits arising from their coupling to the environment, known as decoherence, and the other is the control errors. Control errors can be either systematic in nature, such as drift or cross-talk, or stochastic, such as thermal and shot noise on the control sources. The key is to design the controller in a way such that the impact of stochastic noise on the qubits is less than the intrinsic noise of the qubits, and the systematic noise is fully characterized and mitigated. The possible mitigation approaches include better hardware design, control loops, and quantum control techniques.

Qubit Technology Platforms. The various quantum computer technology platforms in terms of their ability to be integrated in a multi-qubit system architecture. To date, only a few qubit technologies have been assembled and engineered in this way, including superconducting circuits, trapped atomic ions, and neutral atoms. While there are many other promising qubit technologies, such as spins in silicon, quantum dots, or topological quantum systems, none of these technologies have been developed beyond the component level. The research and development of new qubit technologies should continue aggressively in materi-als/fabrication laboratories and facilities. However, their maturity as good qubits may not be hastened by integrating them with modular full-stack quantum systems development proposed here, so we do not focus this roadmap on new qubit development. In any case, once alternative qubit technologies reach maturity, we expect their integration will benefit from the full stack quantum computer approach considered here. It is generally believed that fully fault-tolerant qubits will not likely be available soon. Therefore, specific qubit technologies and their native decoherence and noise mechanisms will play a crucial role in the development of near-term quantum computer systems. There are several systems-level attributes that arise when considering multi-qubit systems as opposed to single- or dual-qubit systems. Each of these critical attributes should be optimized and improved in future system generations:

• -    Native quantum gate expression . Not only must the available physical interactions allow universal control, but high levels of gate expression will be critical to the efficient compilation and compression of algorithms so that the algorithm can be completed before noise and decoherence take hold. This includes developing overcomplete gate libraries, as well as enabling single instruction, multiple data (SIMD) instructions such as those given by global entangling and multi-qubit control gates.

• -    Quantum gate speed . Faster gates are always desired and may even be necessary for algorithms that require extreme repetition, such as variational optimizers or sampling circuits. However, faster gates may also degrade their fidelity and crosstalk, and in these cases the speed to complete the higher-level algorithmic solution should take precedence.

• -    Specific qubit noise and crosstalk properties . Qubit noise properties should be detailed and constantly monitored, for there are many error mitigation techniques for specific or biased error processes that can improve algorithmic success in the software layer. Quantum gate crosstalk is usually unavoidable in a large collection of qubits, and apart from passive isolation of gate operations based on better engineering and control, there are software solutions that exploit the coherent nature of such crosstalk and allow for its cancellation by design.

• -    Qubit connectivity. The ability to implement quantum gate operations across the qubit collection is critical to algorithmic success. While full connectivity is obviously optimal, this may not only lead to higher levels of crosstalk, but ultimately resolving the many available connection channels may significantly decrease the gate and algorithmic speed. Such a trade-off will depend on details of the algorithm, and a good software layer will optimize this trade-off. A connection graph that is software-reconfigurable will also be useful.

• -    High level qubit modularity . For very large-scale qubit systems, a modular architecture may be necessary. Just as for multi-core classical CPU systems, the ability to operate separated groups of qubits with quantum communication channels between the modules will allow the continual scaling of quantum computers. Modularity necessarily limits the connectivity between qubits, but importantly allows a hierarchy of quantum gate technologies to allow indefinite scaling, in principle.

Increasing the number of qubits from hundreds to thousands will be challenging, because current systems cannot easily be increased in size via brute force. Instead, a new way of thinking on how to reduce the number of external controls of the system will be needed to achieve a large number of qubits. This could be approached by further integrating control into the core parts of the system or by multiplexing a smaller number of external control signals to a larger number of qubits. In addition, modularizing subsystems to be produced at scale and integrating these into a networked quantum computer may well turn out to be the optimal way to achieve the necessary system size. Many challenges and possible solutions will only become visible once we start to design and engineer systems of such a size, which will in turn be motivated by scientific applications.

In these series of textbooks, we concentrate our attention on quantum software and hardware engineering approaches for search of intractable classical tasks from computer science, intelligent information technologies, artificial intelligence, quantum software engineering, classical and quantum control. Many solutions are received as new decision-making results of developed quantum engineering IT and have important scientific and industrial applications.

There are two main classes of algorithms where there is a potential quantum advantage - those that rely on Fourier transforms and those that perform searches (Fig. 1).

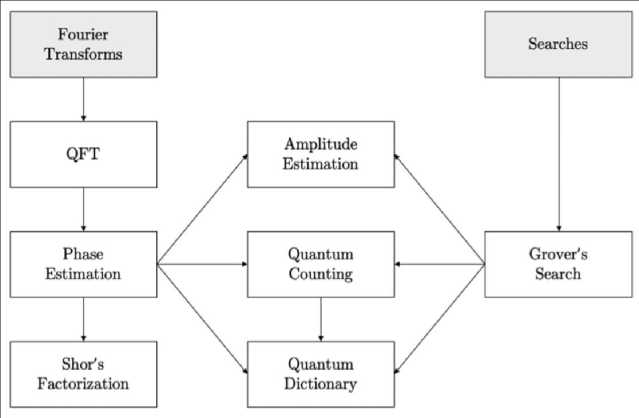
Fig. 1. The two main classes of quantum algorithms [8]

We can think of an oracle as a black box with a contract - the oracle applies the contract when it recognizes an element of a specified subset of the basis states. We call this subset of basis states the good states, and the rest of the states the bad states. The most common contract is to conditionally multiply the amplitudes of the desired basis states by (– 1). Many quantum algorithms rely on oracles to be efficient, and use a placeholder oracle in their definition. Selecting an oracle depends on the nature of the problem that needs to be solved.

A quantum computer is capable of solving a computational task that would require an unreasonable amount of time on any classical supercomputer. Quantum computing is currently moving from an academic idea to a practical reality. Quantum computing in the cloud is already available and allows users from all over the world to develop and execute real quantum algorithms. However, the companies which are heavily investing in this new technology such as Google, IBM, Rigetti, Intel, IonQ, NTU MISiS (Moscow), D-Wave and Xanadu follow diverse technological approaches. This led to a situation where we have substantially different quantum computing devices available thus far. They mostly differ in the number and kind of qubits and the connectivity between them. Because of that, various methods for realizing the intended quantum functionality on a given quantum computing device are available. This review provides an introduction and overview into this domain and describes corresponding methods, also referred to as compilers, mappers, synthesizers, transpilers, or routers.

Quantum Algorithms Realizing on Real Quantum Computing Devices

By exploiting the quantum phenomena such as superposition and entanglement, quantum computers promise to solve hard problems that are intractable for even the most powerful conventional supercomputers. In addition, remarkable progress has been made in quantum hardware based on different technologies such as superconducting circuits, trapped ions, silicon quantum dots, and topological qubits. A recent breakthrough in quantum computing has been the experimental demonstration of quantum supremacy using a superconducting quantum processor consisting of 53 qubits. Current and near-term quantum computing devices are often referred to as Noisy Intermediate-Scale Quantum (NISQ) devices [9], to highlight their limited size and imperfect behaviour due to noise. However, while quantum technologies need to improve coherence times and gate fidelities to achieve overall lower error rates, quantum computing in the cloud is already a reality offering small quantum computing devices that are capable of handling basic quantum algorithms. Companies such as Google, IBM, Rigetti, and Intel, have already announced 72-qubit, 50-qubit, 128-qubit, and 49-qubit superconducting devices, respectively.

In these quantum processors, qubits are arranged in a 2D topology with limited connectivity between them and in which only nearest-neighbor (NN) interactions are allowed. This is one of the main constraints of today’s quantum devices and frequently requires the quantum information stored in the qubits to be moved to other adjacent qubits – typically by means of SWAP operations. The quantum algorithms, which are described in terms of quantum circuits, neglect the specific qubit connectivity and, therefore, cannot be directly executed on the quantum computing device but need to be realized with respect to this and others constraints. The procedure of adapting a circuit to satisfy the quantum processor restrictions is known as the compiling, mapping, synthesis, transpiling, or routing problem. The mapping process often causes an increase of the number of quantum operations as well as the depth (number of time-steps) of the quantum circuit. The success rate of the algorithm is consequently reduced since quantum operations are error prone and qubits easily degrade their state over the time due to the interaction with the environment. To minimize the negative impact of the mapping, it is required to develop efficient methods that minimize the resulting overhead – especially for NISQ devices in which the lack of active protection against errors will make long computations unreliable.

The basics of quantum computing and, afterwards, will present two mapping approaches for realizing quantum algorithms on two different superconducting transmon devices. The first targets an IBM processor, the IBM QX4, that consists of five qubits. The second is meant to execute quantum circuits on the Surface-17 chip composed of seventeen quits (larger quantum architectures are available from both vendors, but to keep the following descriptions and examples simple). To evaluate the effect of a quantum gate on a quantum state, the respective vector (describing the quantum state) simply has to be multiplied with the respective matrix (describing the gate). The finite set of gates form a universal gate set, i.e., all quantum functions can be realized by them. Sequences of quantum operations finally define quantum algorithms which are usually described by high-level quantum languages (e.g. Scaffold or Quipper), quantum assembly languages (e.g. OpenQASM 2.0 developed by IBM or cQASM), or circuit diagrams.

For this purpose, circuit diagrams are using such as those in Fig. 2(a) as representation of quantum algorithms in the following.

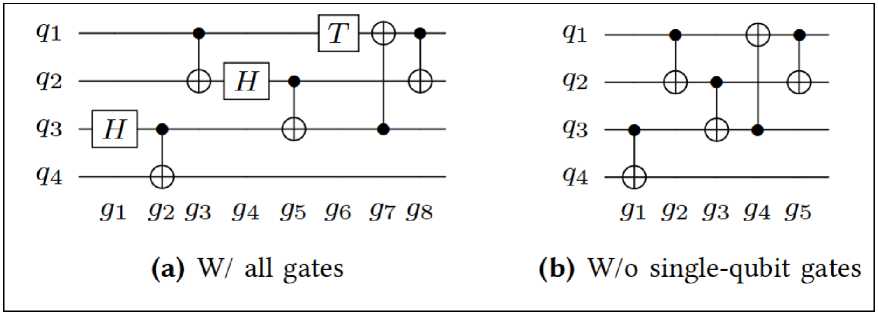
Fig. 2. An example of a quantum circuits

Here, qubits are visualized as circuit lines that are passed through quantum operations, which are denoted by boxes including their respective denominator in case of single-qubit operations and a black dot and a ⊕ symbol for control qubit and target qubit, respectively, in case of a CNOT operation. Note that the qubit lines do not refer to an actual hardware connection as in classical logic, but rather define in which order (from left to right) the respective operations are applied. Physical implementations of quantum computers may rely on different technologies. For example, will focus on quantum computers based on superconducting transmon qubits on silicon chips. Here, the operations are conducted through microwave pulses transferred into and out of dilution refrigerators, in which the quantum chips are set at an operating temperature of around 15 mK. Communication into, out of, and among the qubits is done through on-chip resonators.

As in classical computers, quantum algorithms described as programs using a high-level language have to be compiled into a series of low-level instructions like assembly code and, ultimately, machine code.

As sketched in Fig. 3, in a quantum computer these instructions need to be ultimately translated into the pulses that operate on the qubits and perform the desired operation.

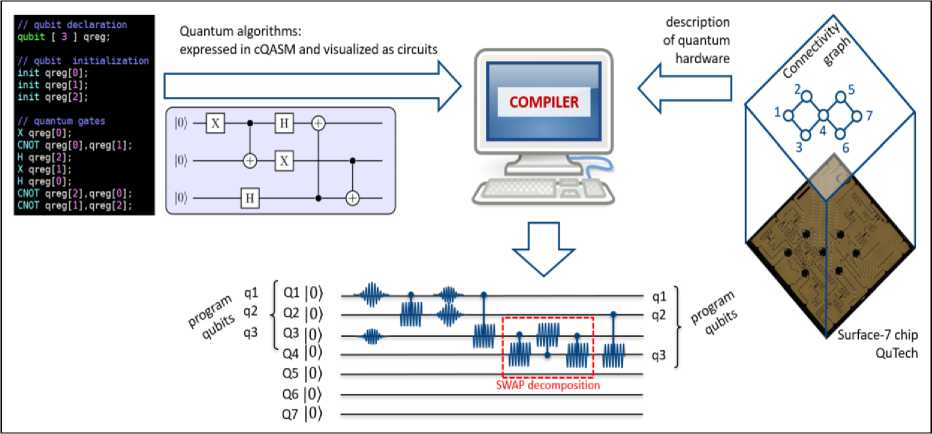
Fig. 3. Sketch of the mapping process for quantum algorithms

[The compiler depicted in the center receives two kinds of inputs: from the left it receives the quantum algorithm in terms of a sequential list of quantum gates to be executed (expressed in cQASM) and from the right the description of the machine, possibly including the control electronics in addition to the quantum hardware. Its output is a series of scheduled operations that can be executed by the machine and is depicted at the bottom in terms of the control signals that implement it. The initial placement of the program qubits q1, q2, q3 may differ from the final placement. For simplicity we have assumed that the CNOT and H gates are available in the machine’s gate set instead of the native gates of Surface-7].

Thus, quantum algorithms can be described as a list of sequential gates, each acting on a few qubits only, and visualized in terms of quantum circuits. Quantum circuits cannot be directly realized on real quantum processors, but need to be adapted to the specificity of each quantum device. In addition to preserving all dependencies between the quantum operations, compilers of quantum circuits must perform three important tasks: 1) express the operations in terms of the gates native to the quantum processor, a task called gate decomposition, 2) initialize and maintain the map specifying which physical qubit (qubit in the quantum device) is associated to each program qubit (qubit in the circuit description, sometimes called logical qubit in the literature), a task called placement of the qubits, and 3) schedule the two-qubit gates compatibly with the physical connectivity, often by introducing additional routing operations.

Remark . Often do not elaborate on the gate decomposition, apart from observing that most current quantum devices provide a native gate set that is equivalent and often larger than the universal gate set. The two remaining tasks are performed by the circuit mapper within the compiler. Notice that the task of initializing the qubit placement is expected to play an important role in near term devices, but will probably have a relatively limited impact when algorithms grow in depth. For this reason, the main focus will be on the problem of minimizing the routing overhead, arguably the most impactful mapping task especially when excluding quantum error correction.

The problem is simply stated: one needs to schedule a two-qubit gate but the corresponding program qubits are currently placed on non-connected physical qubits. The placement must therefore be modified with the goal of moving the involved qubits to adjacent connected ones. Quantum information cannot be copied and there is essentially one way of transferring it, namely by applying SWAP gates that effectively exchange the state of two connected qubits.

Another approach is based on teleportation, corresponding to long-distance transfer of the qubit state. It requires the creation of multi-qubit entangled states that are preliminarily distributed across the qubit register and that can be consumed to transfer a qubit state. Since the distribution of the entangled state requires SWAP gates, the teleportation approach can be seen as a SWAP-based routing with relaxed time constraints.

The functionality of the circuit mapper, which is usually embedded in the compiler, is sketched in Fig. 2. It requires two separate inputs, one related to the abstract algorithm to implement and the other associated with the quantum processor chosen for its execution. The former is usually provided in terms of high-level code or Quantum Assembly Language (QASM) instructions, an explicit list of low-level operations corresponding to single-and two-qubit gates, and can be visualized in the form of quantum circuits. The latter corresponds to a description of the hardware, from the qubit topology and connectivity to the electronics that generate and distribute the control signals. The compiler is in charge of decomposing the operations in terms of the gates native to the processor and then of the mapping process. The mapping process is comprised of the initial placement of qubits, qubit routing, and operation scheduling.

Several solutions have already been proposed for solving the mapping problem; that is, to make quantum circuits executable on the targeted quantum device by transforming and adapting them to the constraints of the quantum processor. Most of the works focus on NISQ devices such as the IBM or Rigetti chips as they are accessible through the cloud. The proposed mapping solutions differ and therefore can be classified according to the following characteristics:

• -    Quantum hardware constraints: one of the main restrictions of current quantum devices is the limited connectivity between the qubits. Different quantum processors, even within the same family, can have different topologies such as a linear array (1D), a 2D array with only nearest-neighbor interactions, or more arbitrary shapes. Although most of the works on mapping focus on the qubit connectivity constraint, there are other restrictions that originate from the classical control part and that reduce the parallelizability of quantum gates. This kind of constraint become more and more relevant when scaling-up quantum systems as resources need to be shared among the qubits.

• -    Solution approach and methodology: exact approaches are feasible when considering relatively small number of qubits and gates, giving minimal or close-to-minimal solutions. However, they are not scalable. Approximate solutions using heuristics can be used for large quantum circuits. Some used methods are (Mixed) Integer Linear Programming ((M)ILP) solvers, Satisfiability Modulo Theory (SMT) solvers, heuristic (search) algorithms, decision diagrams, or even temporal planners and reinforcement learning.

Cost function: there are different metrics that can be optimized in the mapping process. The most common cost functions are the number of gates (i.e. minimize the number of added SWAPs) and the circuit depth or latency (i.e. minimize the number of time-steps of the circuit). Recent works started optimizing directly for circuit reliability (i.e. minimize the error rate by choosing the most reliable paths).

Solution features: In addition to the just mentioned characteristics, there are other important features that can lead to better solutions. Some examples are the look-back strategy in the routing that refers to taking into account the previous already scheduled operations when selecting the routing path or the look-ahead feature that considers not only the current two-qubit gates that need to be routed and scheduled but also some of the future ones with some weights. Besides that, also pre-processing steps dedicated to particular quantum functionality have shown to be extremely beneficial.

Certain machines allow for extensive pre-compilation of the algorithms that solely excludes the routing operations and parallelization information. In this case the mapper receives QASM code that uses only the one- and two-qubit gates available to the device.

The output only adds routing operations. These machines require:

• -    symmetric two-qubit gates;

• -    homogeneous single-qubit gate set;

• -    the possibility of measuring any qubit in the same basis.

Here, SWAP gates are needed only to overcome the connectivity limitations. The mapper needs to know how to decompose SWAP gates into the available gate set. Often there are multiple ways to do so, for example each decom-position originates a second one obtained by exchanging the role of two qubits involved in the first one. While the transmon architecture of Surface-17 chip exhibits the three properties, they are not required for functioning quantum devices. When the properties are not satisfied, the mapper cannot fully separate the gate decomposition and routing tasks. When the two-qubit gates are asymmetric, decisions concerning the addition of extra gates must be made at the time of routing and scheduling. For example, when CNOTs are used as in the IBM architecture, extra Hadamard gates may be required to invert the role of the control and target qubits. This can be known only at the time of routing, i.e. when the qubit placement in the CNOT is known. When the available native one-qubit gates differ from (physical) qubit to qubit, the scheduling involves two steps.

Consider that one needs to schedule gate U acting on the k-th program qubit. In this case it is required to 1) compute the sequence of available gates that implements, or approximates, U for the different physical qubits (or at least those at short distance from the physical qubit currently associated to program qubit k), and 2) add the cost of the routing. Selecting the better option therefore requires performing multiple gate decompositions and can be done only at scheduling time when the placement is known. To date all architectures, provide the same set of one-qubit gates per physical qubit, but this may change due to the pressure of reducing control resources or when the gate fidelity is used as the metric to guide mapping decisions. Finally, when not all qubits can be directly measured or when the available measurements differ from qubit to qubit, additional gates are required. In the first case to move the quantum state towards measurable qubits, and in the second case to adapt the measurement basis.

Despite their differences, all mappers need an internal representation of key quantities and these can be combined in the concept of the execution snapshot. As the name suggests, the execution snapshot is a complete description of the algorithm and its current, usually partial, schedule.

It contains:

• -    the dependency graph of the algorithm with the indication of which gates have already been scheduled;

• -    the initial placement that associate each program qubit to a physical qubit;

• -    the current placement of the qubits

• -    the partial schedule with the timing information and explicit parallelism

• -    the settings of the control electronics for the execution.

The data structure specifying the execution snapshot varies from mapper to mapper. Here it provides an intuitive one: the dependency graph is a directed, acyclic graph with nodes representing the quantum gates and edges indicating dependencies (the target node corresponds to the gate that depends on the source node). Nodes can have one of two colors, differentiating the gates already scheduled from those that need to be scheduled. An additional color may mark the gates that can be scheduled next according to the algorithmic dependencies. Qubit placement is represented by an array of integers of size equal to the number of physical qubits: the k-th entry corresponds to the index of the program qubit associated to the k-th physical qubit, apart from a special integer indicating that the qubit is “free” in situations where the program requires less qubits than those present in the quantum hardware. Finally, the schedule with timing information can be provided as a table by discretizing the time into clock cycles, the greatest common divisor of the gates’ duration. This table also includes any additional gate from gate decomposition and routing. The mapper has to take into account the constraints from the control electronics. To this end one needs a way to track, for every clock cycle in which a certain gate can be performed according to the logical dependencies, if that gate can be executed compatibly with all the gates already scheduled. Therefore, the mapper needs to be aware of how the set of compatible gates (i.e. those part of the physically available gate set and that do not conflict with gates already scheduled) changes at each clock cycle, and update it dynamically. The conceptually simplest method is to keep an explicit list of the compatible gates for each physical qubit, but this may not be the most efficient implementation. In fact, more compact representations are derivable for specific architectures.

Devices based on superconducting circuits no mean the only approach to scalable quantum devices. Multiple physical implementation of quantum processors is being currently developed, including but not limited to trapped ions, silicon quantum dots, photonics, neutral atoms, and topological systems. The maturity of each technology is at a different point and the challenges to scalability are also different. We are interested to provide a few examples in which particular physical implementations provide unique features. We only present three of them for illustration purposes. Most architectures are limited to a planar connectivity between qubits, but trapped ions provide all-to-all connectivity, at least inside groups of tens of ions. This is originated by their long-distance Coulomb interaction and mediated by their collective vibrational modes. However, this desirable property comes at the price of reduced two-qubit gate parallelism. Finally observe that multi-qubit gates are also available for trapped ions and this may require an enlarged instruction set. Photonics architectures are uniquely positioned for tasks that combine computation and communication, like at the nodes of quantum repeaters’ networks. However, they are limited to demolition measurements in which the qubit is “destroyed” when measured since the photon is absorbed by the detector. One can generate a new photon to re-initialize the qubit state. In silicon quantum dots the role of qubits is played by the spin of electrons confined in electromagnetic potential wells called dots. The simplest scheme is one electron per dot, but alternative configurations are also considered. Two-qubit gates are implemented via the exchange interaction between two electrons in nearby dots. However certain dots can be momentarily empty and electrons can be moved to empty dots in a way that maintains the qubit coherence, the so-called shuttling operation. The electron movement can be interpreted either as a change in the device connectivity or as an alternative qubit routing not based on SWAP gates. Specialized mappers are required to take full advantage of these capabilities.

During the compilation process quantum circuits need to be modified to comply with the constraints of the quantum device. This usually results in an increase of the number of gates and the circuit depth, which affects negatively the reliability of the computation. Therefore, minimizing this mapping overhead is crucial, especially for NISQ devices in which no or hardly any error protection mechanisms will be used. Two examples of mappers developed for two specifics superconducting transmon processors, the IBM QX4 and the Surface-17, where different solution approaches are used. In addition, other device types, the internal data representations used by the mappers and described the peculiarities of other possible physical implementations of quantum processors. There are still several open questions requiring the attention of the community working on mappers of quantum algorithms.

First, what is the best metric to optimize? Most of the works use as the optimization metric either the number of gates or the circuit depth. Recent works started considering the expected reliability of the overall quantum computation. New metrics, or possibly a combination of the existing ones, need to be investigated.

Secondly, should aim for machine-specific solutions or more general-purpose and flexible ones capable of targeting different quantum devices and technologies and different optimization problems? So far, the proposed mappers can be considered ad-hoc solutions that are mostly meant for a particular chip or similar kind of processors in which qubits are moved by SWAPs.

While general-purpose mappers would avoid repeating the development effort for each device, the risk is that general optimization strategies will not take full advantage of the hardware capabilities. In addition, the change of the quantum technology may require very different mapping strategies.

Third, what is the good balance between the obtained solution and the time required to compile the circuit? It is necessary to analyze the trade-off between mapping optimizations and runtime, especially for large-scale quantum algorithms.

Finally, it is important to mention that these optimizations should consider both the quantum device and the quantum application characteristics. In this direction, proposes an approach which takes the planned quantum functionality into account when determining an architecture.

An application of an algorithm is only as efficient as the oracle it supplies. Let us consider the example of quantum gate-based computing approach apply qualitative description of quantum amplitude amplifier algorithm. There are multiple ways to implement the contract of multiplying the amplitudes of the recognized states by (– 1):

• 1.    Most texts in quantum computing use a nice trick that efficiently performs the multiplication with a

• 2.    Recall the ZXZX gate sequence, which multiplies the amplitudes of a state by (– 1) (Fig. 5). This works on any state, unlike the trick above, but at the cost of an increased number of gates.

single qubit. Prepare the state of an ancillary qubit with amplitudes a₀ = —and a_x = —, using an 0 ₂ 1 ₂

HX gate sequence on the default state. We then apply an X gate to that ancillary qubit, which flips the phase of control qubits (Fig. 4). Note that the trick only works on this specific state.

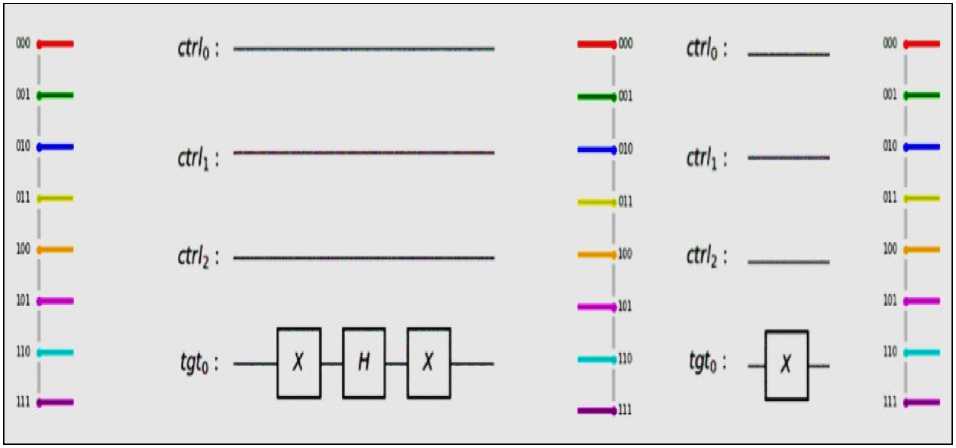
Fig. 4. A circuit that multiplies the state by (– 1) using a specially-prepared state, applied twice for illustration. [The target qubit is not shown in the histograms]

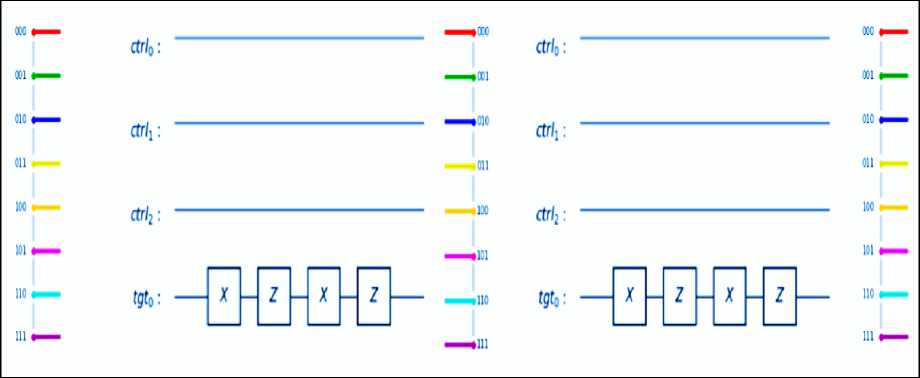
Fig. 5. A circuit using the ZXZX gate sequence, which multiples any state by (– 1), applied twice for illustration. [The target qubit is not show in the histograms]

Let’s take a look at a simple oracle, recognizing the basis states (binary strings) representing even integers. For a quantum system with three qubits, the oracle should negate the amplitudes of the basis states ending in 0, e.g. 000, 010, 100, and 110 (Figs 6 and 7).

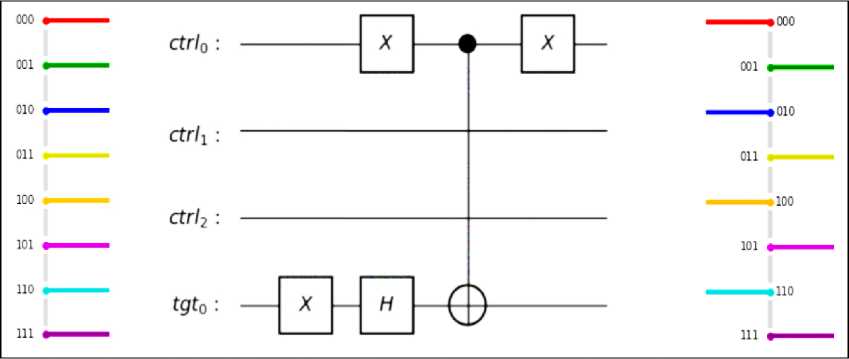
Fig. 6. An oracle that recognizes the even states and multiplies their amplitudes by (– 1) using the single-qubit trick

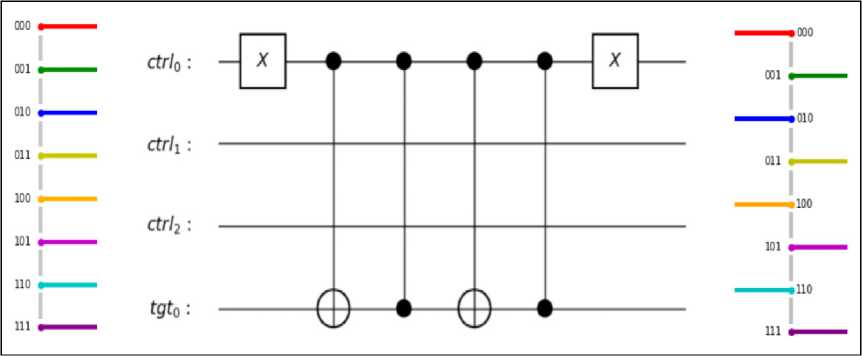
Fig. 7. An oracle that recognizes the even states and multiplies their amplitudes by (– 1) using the ZXZX gate

Next, let’s look at an oracle that recognizes a particular set of basis states specified element by element. In this example the oracle must examine all of the basis states, and multiply their amplitudes by (– 1) only if all qubits match an element in the given subset. We will need to introduce ancillary qubits, used as the controls of the multiplication gate(s) on the target qubit (see below Figs 8 and 9).

Note that we have to apply a control gate to the qubit at index j = 0. Recall the control gates are applied when the control qubit is 1. In order to match 0, we apply an X to that qubit. In the resulting state, the amplitudes of the even outputs have been multiplied by (– 1), and the amplitudes of the odd outputs remain unchanged.

Next, let’s look at an oracle that recognizes a particular set of basis states specified element by element, e.g. { 101,110 } . In this example the oracle must examine all of the basis states, and multiply their amplitudes by (– 1) only if all qubits match an element in the given subset. We will need to introduce n – 1 ancillary qubits, used as the controls of the multiplication gate(s) on the target qubit (Figs 8 and 9).

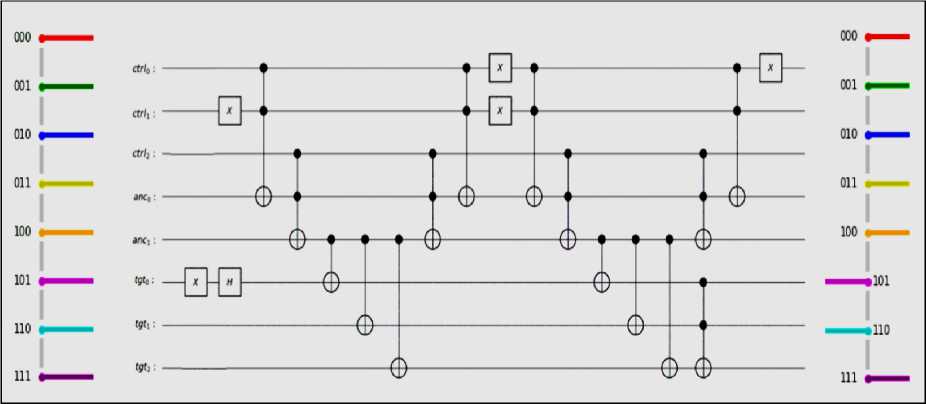
Fig. 8. An oracle that recognizes the states in a set, and multiplies their amplitudes by (– 1) using the single-qubit trick

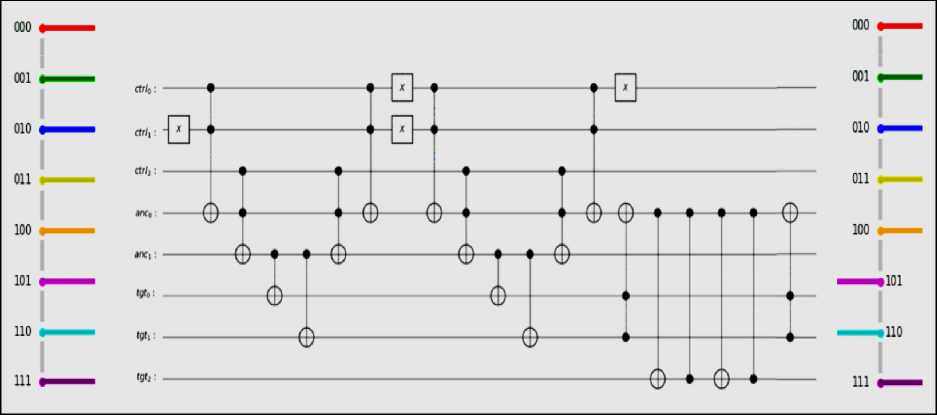
Fig. 9. An oracle that recognizes the states in a given set, and multiplies their amplitudes by (– 1) using the ZXZX gate

While this is a useful oracle, it is not very efficient, as it requires a large number of controlled gates to match all bits in the recognized basis states. Oracles can also be used for satisfiability problems like 3-SAT, in which we create a black box that recognizes the basis states that satisfy a Boolean expression. While we won’t provide an in-depth discussion, there is one in IBM’s introduction. Another interesting oracle is one that recognizes prime numbers, which could potentially be built using Shor’s algorithm. Here we concentrate our attention on quantum search problem in instructed data base.

In an efficient quantum computing we want to increase the probability of some desired outputs, and therefore decrease the number of times we need to repeat the computation. We have already seen how Phase Estimation can help increase the amplitudes of the outputs that best approximate a parameter. Grover’s algorithm performs amplitude amplification by using an oracle that recognizes a single basis state. The algorithm uses what is called the Grover iterate - consisting of a sequence of two steps (an oracle O and the diffusion operator) - which is applied a specific number of times. We discussed oracles in the previous subsection. The diffusion operator D has the net effect of inverting all amplitudes in the quantum state about their mean. This causes all the amplitudes of the good states to be scaled by at least , while the ampli-N tudes of all other outcomes (the bad states) decrease. If one thinks of the computation as a die, the probability of one of the faces is dramatically increased. Note that the amplitudes remain real throughout the application of the oracle and the diffusion operator. A complete implementation of Grover’s algorithm is provided in Appendix.

As an example, let’s examine a three-qubit quantum state with the desired outcome being 101, using the set-based oracle described in the previous subsection (Fig. 10).

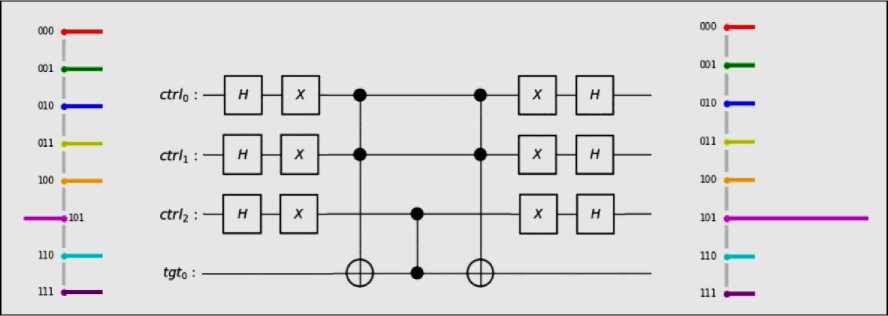
Fig. 10. A three-qubit state after a single pass of the oracle, which is then passed to the diffusion operator (multiplication of amplitudes by (– 1) not shown in the circuit)

We repeat the application of the oracle and the diffusion operator for I N V I iterations (Fig. 11).

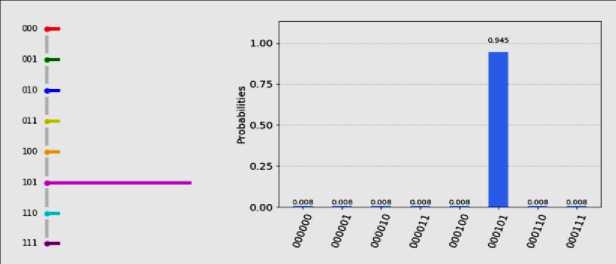
Fig. 11. The result of Grover’s algorithm after I V N = 8 = 2 I iterations of the oracle and diffusion operator

Note that it is possible to over-iterate, which would decrease the magnitude of the desired output during the application of the diffusion operator (Fig. 12).

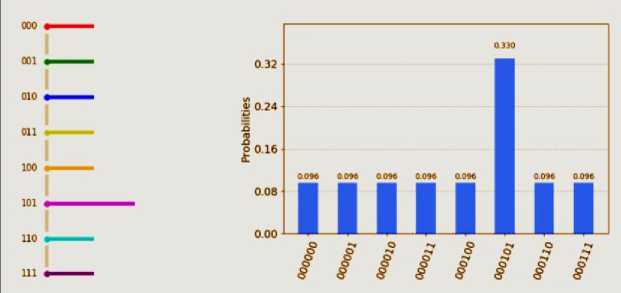
Fig. 12. The result of Grover’s algorithm after ^ V N = 8 + 1 = 3 j iterations of the oracle and diffusion operator

Therefore, any quantum computation can be simulated classically; the key question is about the efficiency. Much effort has been made trying to pin down the power of quantum computers based on the machinery of the computational complexity theory. In particular, the class of computational (decision) problems that can be solved efficiently by a quantum computer is called BQP (bounded-error quantum polynomial time); the counterpart for classical computers is called P (polynomial time). Of course, BQP cannot be less than P; in principle quantum computers can simulate classical computers efficiently. The point is that the foundation of quantum computation cannot be established without a proof showing that BQP is strictly larger than P (i.e. BQP ^ P). In this sense, this question is as interesting as the famous challenge of proving P ^ NP (non-deterministic polynomial time). A well-known instance of an NP problem is the factoring problem; Shor’s quantum algorithm is capable of solving the factoring problem in polynomial time, which is not achievable with the best classical algorithm discovered so far.

However, we still cannot rigorously exclude the possibility of the existence of an efficient classical algorithm for factoring. Although again without a proof, it is commonly believed that quantum computers are unable to solve some of the NP problems. In fact, the proof of this statement (if true) provides a possible path to prove P ^ NP.

Quantum supremacy. A potentially less demanding question would be, when do we expect a quantum computer to be able to perform some well-defined tasks (not necessarily related to any practical problem) that can-not be simulated with any currently available classical device, within a reasonable time? Once achieved, the status is called “quantum supremacy”. One may ask, what about Grover’s search algorithm, which provides a quadratic speed-up over the classical search? Can we say that we can already achieve quantum supremacy with Grover’s algorithm? The problem is that, instead of taking the large N limit, quantum supremacy requires us to determine the actual number of qubits and gates that can no longer be simulated by classical computers within a reasonable time.

To elaborate further, we remark that there can be two notions of classical simulation, namely “strong simulation” versus “weak simulation”. Strong simulation refers to the cases of calculating the transition probabilities, or expectation values of observables, to a high accuracy in polynomial time. Weak simulation requires the probability distributions to be accurately reproduced, which involves ‘sampling’ the different outcomes of the quantum devices. Some quantum circuits that cannot be strongly simulated with an efficient classical means may have efficient classical methods for weak simulation. However, we should be careful about the accuracy requirement in the simulation tasks. For example, for many decision problems, it may be sufficient to determine the transition amplitudes to within an additive error, instead of multiplicative error. In other words, the classical simulability of quantum computational problems depends on the accuracy requirement. Currently, there are three popular approaches for achieving quantum supremacy (see Fig. 13), namely (i) boson sampling, (ii) sampling IQP (instantaneous quantum polynomial) circuits, and (iii) sampling chaotic quantum circuits.

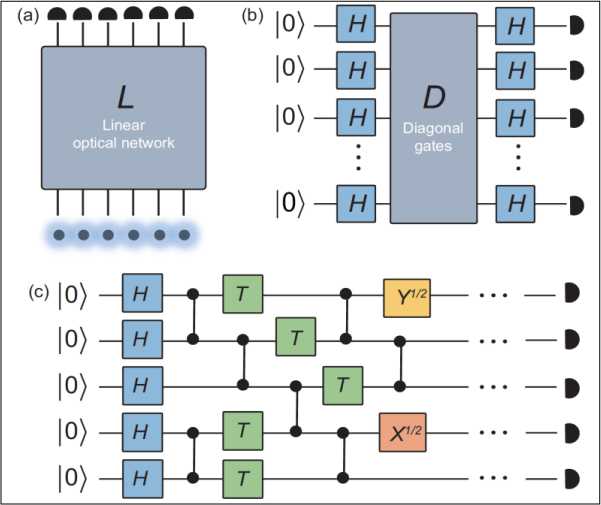
In all of these approaches, the distributions of different bit strings or photon numbers are sampled from the quantum devices. Furthermore, they all involve the assumption that classical computers are unable to efficiently determine the transition amplitudes, and/or reproduce (or approximate) the distributions of quantum devices performing these tasks, in the sense of both strong and weak simulations.

In boson sampling, single photons are injected into different modes of a linear optical network. The task is to determine the photon distributions at the output ports. The key feature of boson sampling is that the transition amplitudes are related to the permanents of complex matrices, which are in general very difficult to calculate exactly, or approximate to within a multiplicative error; these problems belong to the #P-hard complexity class. Moreover, efficient weak simulation of boson sampling is believed to be impossible, unless the polynomial hierarchy collapses to its third level. However, a recent numerical study suggests that, in order to achieve quantum supremacy with boson sampling, one needs to simultaneously generate at least 50 or more single photons, which is still highly technologically challenging. An interesting question is whether linear optics, in the setting of boson sampling, can be applied to solve decision problems. In this case, the transition amplitudes may need to be determined to an additive error. However, a large class of decision problems associated with boson sampling can be simulated by a classical computer, settling an open problem by Aaronson and Hance.

IQP circuits represent a simplified quantum circuit-based model. The initial state starts from the all-zero state, 00 0) , followed by applying Hadamard gates to each qubit. Then, diagonal gates are applied to the qubits, followed by applying Hadamard gates to each qubit again. The argument of showing the complexity in simulating IQP circuits is similar to that of boson sampling. In fact, the complexity of boson sampling was inspired by the complexity results of IQP circuits. However, when subject to noise, IQP circuits may become classically simulable.

Lastly, chaotic quantum circuits refer to the class of quantum circuits where two-qubit gates are applied regularly, while single-qubit gates are applied randomly from a gate set. The output distributions of these circuits approach the so-called Porter–Thomas distribution, which is a characteristic feature of quantum chaos. Recently, there have been several numerical investigations aiming to explore the ultimate limit of classical computing in simulating low-depth quantum circuits. For the ideal cases, one needs to consider both the qubit number and circuit depth for benchmarking quantum supremacy. However, in the presence of noise, these chaotic circuits may also become classically simulable for high-depth circuits.

Finally, other than these three approaches, one should expect that quantum supremacy can be achieved for many practical applications, e.g. simulation of quantum chemistry or quantum machine learning.

What’s a quantum circuit? A quantum circuit can be a tricky thing. Quantum computing promises to be faster than classical computing in some, but not all computational problems. Whether quantum computers can be faster than classical computers depend on the nature of the problem being solved. When speedups are possible, the magnitude of the speedup also depends on the nature of the problem. For example, in certain types of problems, the solving time with quantum computing could reduce to about the square root of the solving time with classical computing. That is, a problem that would require one million operations on a classical computer might require 1,000 operations on a quantum computer.

What’s a qubit? The basic memory units in a quantum computer are qubits, which are a generalization of the bits on a classical computer. A classical bit can take two distinct values, 0 and 1. At any given time, a bit has exactly one of these two values. As such, a bit is similar to a coin sitting on a table: it can be either in a head-up state (which we can consider to be the equivalent of a bit set to 0) or in the head-down position (bit set to 1). In contrast, a qubit can have more values than just 0 and 1. At a given time, the state of a qubit can be a combination of 0 and 1, called superposition. Using the coin analogy, superposition resembles a coin spinning in the air. Put informally, it’s like the qubit is in both basic states (0 and 1) at the same time. More formally, superposition is a weighted combination between the basic states 0 and 1.

How do quantum algorithms work? Quantum algorithms work by applying quantum operations (called quantum gates) on subsets of qubits. Quantum gates are analogous to instructions in a classical program. A quantum algorithm represented using gates is called a quantum circuit. Current models for quantum computing require quantum algorithms to be specified as quantum circuits on idealized hardware, ignoring details that could be specific to the actual hardware. This makes quantum algorithms more portable across different types of hardware, and it allows programmers to focus on the solution to the problem, not on the details specific to a given hardware. Thus, a quantum program needs to be translated into a representation that a given quantum computer can execute. This is known as quantum circuit compilation (QCC). (See the Fig. 14 for an illustration.)

Fig. 14. Structure of quantum circuit compilation (QCC) processes

Compiling a quantum circuit requires adding additional gates that move qubit states to locations where the desired gate could act upon them under the physical constraints of the actual quantum processor. In a way, this is similar to how a classical program is compiled from a language that programmers understand (e.g., C++) into a binary representation that the hardware can execute. Among potentially many compiled circuits that could correspond to a given quantum program, circuits with a shorter execution time are preferable. Part of the reason is a phenomenon known as decoherence: qubit states may get altered after a short time, due to factors such as interaction with the physical environment. For example, the commercial IBM 20-qubit environment has a coherence time of about 100 ms. Circuits with a shorter execution time could finish their running before decoherence occurs. However, computing a compiled circuit with a shortest possible execution time could come at a cost. Specifically, the question is whether such compilations can be performed efficiently (i.e., in a reasonably short time). So far this has been an open question.

Quantum computing can enable a variety of breakthroughs in research and industry in the future. Although some quantum algorithms already exist that show a theoretical speedup compared to the best-known classical algorithms, the implementation and execution of these algorithms come with several challenges. The input data determines, e.g., the required number of qubits and gates of a quantum algorithm. An algorithm implementation also depends on the used Software Development Kit which restricts the set of usable quantum computers. Because of the limited capabilities of current quantum computers, choosing an appropriate one to execute a certain implementation for a given input is a difficult challenge that requires immense mathematical knowledge about the implemented quantum algorithm as well as technical knowledge about the used Software Development Kits. Thus, a roadmap for the automated analysis and selection of implementations of a certain quantum algorithm and appropriate quantum computers that can execute the selected implementation with the given input data must be presented.

Quantum Computing has entered the NISQ (Noisy Intermediate-Scale Quantum) era where it may surpass classical computing with even imperfect quantum hardware. As one of its most promising applications, quantum machine learning is drawing intense attention for its potential supremacy on solving large-scale real-world learning tasks with quantum computers. Many algorithms have been proposed along this route, e.g., quantum supporting vector machine for classification problems, quantum principal component analysis and quantum generative adversarial learning. To enable quantum machine learning algorithms on NISQ processors, a popular approach is to construct quantum neural-network (NN) models with parameterized quantum circuits (PQC) that is trained by classical optimization algorithms. Such hybrid quantum-classical models have universal approximation capabilities and are able to achieve classically intractable feature learning tasks. Various applications have been put forward for quantum simulation of molecules combinatorial optimization and machine learning problems.

All these demands call for a hardware-friendly quantum machine learning scheme that can be efficiently deployed on NISQ processors. Ideally, the scheme should provide an end-to-end data pipeline that yields learning output from the input data with as less as possible hand-designed modules, and the entire physical implementation should be straightforward with only few ad-hoc elements/parameters to be selected.

Quantum computing is a promising field that may in future enable breakthroughs in various areas such as computer science, physics, and chemistry. The unique characteristics of quantum mechanics, such as superposition and entanglement, are the reasons why quantum computing is more powerful than classical computing for certain problems. In fact, some quantum algorithms already exist that show a theoretical speedup over their best-known classical counterparts. For example, the Shor algorithm provides an exponential speedup in factorizing numbers. With a large enough quantum computer, this algorithm could break cryptosystems such as the commonly used RSA. However, there are several challenges regarding the execution of quantum algorithms, which are considered in the following.

There exists a multitude of different implementations for quantum algorithms that are only applicable to certain input data, e.g., in terms of the number of qubits required for its encoding, which we refer to as input size. These implementations differ from each other in various aspects, e.g., the required number of qubits and operations. Thereby, both numbers often depend on the input data. This means that the input data influences whether or not a particular quantum algorithm implementation is executable on a certain quantum computer: If the number of required qubits or operations is higher than the number of provided qubits or the decoherence time of the quantum computer, the implementation with the given input cannot be executed on this machine. Also, error rates, fidelity, and qubit connectivity of a quantum computer play an important role in the decision.

The Quantum Computer Stack. Computer architectures are often defined in terms of their various levels of abstraction or “stack,” from the user interface and compiler down to the low-level gate operations on the physical hardware itself. The quantum computer stack can be defined similarly, as depicted in Fig. 15.

Quantum Software

Express in native gates/connectivity

Deploy error correction strategy

Qubit Technology

Interface control fields with qubit system

Fig. 15. Advances in all levels of the quantum computer stack, from algorithms and quantum software down to control engineering and qubit technology, will be required to bring quantum computers to fruition

[Scientific opportunities are expected at every level and at the interfaces between levels. At the highest levels, quantum computer algorithms are expected to advance many fields of science and technology. Midstack, the compilation and translation of quantum gates will allow for algorithmic compression to accelerate performance, while error-correction techniques will mitigate quantum computing errors. At the lowest levels, new ways to control interactions between qubit technologies may lead to better performance. Future capable qubit technologies will require tight integration with the other layers of the stack to realize their potential.]

However, the various levels of the quantum computer stack (especially the qubits themselves) are not yet cheap and commoditized like classical computer technology. So, it is critical that quantum computers be designed and operated with the entire stack in mind, with a vertical approach of co-designing quantum computer applications to their specific hardware and all levels in between for maximum efficiency. Indeed, early quantum computer system development may parallel current classical application-specific integrated circuits (ASICs) used for specific and intensive computations such as molecular structure or machine learning.

We list the levels of the quantum computer stack and point to various approaches at each level. The key to co-designing quantum computers is to acknowledge the great opportunities at the interfaces between different levels of the stack, which requires a high level of interdisciplinarity between the physical sciences, engineering, and computer science. In this textbook series, we illustrate how various levels of the quantum computer stack (see Photo below) will be exploited for several use cases.

Extreme susceptibility of quantum computation to noise is one of the crucial factors that hinder the development of large-scale quantum computers. By the means of optimizing gate count in a quantum circuit, it is possible to significantly reduce hardware errors and increase the accuracy of quantum computation. Optimal (or near-optimal) circuit compilation is an extremely challenging and still open problem due to addition- al constraints imposed by hardware configuration, such as restricted qubit connectivity and hardware-native gate set.

Efficient compilation of quantum algorithms and circuit optimisation is vital in the era of noisy intermediate scaly noisy devices. While there are multiple quantum circuit compilation and optimisation frameworks available, such as Qiskit (IBM), Pytket (CQC), Cirq (Google), there is no good way to compare their performance.

This problem solves by providing the solution for cross-benchmarking of quantum compilers. The comparison of different quantum compilation frameworks is based on a set of relevant metrics, such as final gate count, circuit depth, compiler runtime etc. Moreover, Arline Benchmarks allows user to combine circuit compilation and optimisation routines from different providers in a custom compilation pipeline to achieve the best performance. Quantum applied machine learning will make quantum algorithms run on NISQ computers and solve state-of-the art computational problems.

In addition, there is currently no accepted common quantum programming language. As a result, most quantum computer vendors have their proprietary Software Development Kit (SDK) for developing and executing implementations on their quantum computers. However, this tightly couples the implementation of a quantum algorithm to a certain kind of quantum computer. As a result, choosing an implementation for a quantum algorithm to be executed for given input data as well as selecting an appropriate quantum computer is a multi-dimensional challenge that requires immense mathematical knowledge about the implemented algorithm as well as technical knowledge about the used SDKs. Hence, (i) the selection of a suitable implementation of a quantum algorithm for a specific input and (ii) the selection of a quantum computer with, e.g., enough qubits and decoherence time is currently one of the main problems when quantum computing is used in practice. A roadmap for a Noisy Intermediate-Scale Quantum (NISQ) Analyzer that analyzes and selects (i) an appropriate implementation and (ii) suitable quantum hardware depending on the input data for a chosen quantum algorithm is needed.

The approach is based on defining selection criteria for each implementation described as first order logic rules. Thereby, we take into account the number of required qubits of the implementation and the number of provided qubits of eligible quantum computers, while vendor-specific SDKs are also heeded. In addition, the number of operations of an implementation is determined and the corresponding decoherence time of the different quantum computers are considered. To determine the number of qubits and operations of an implementation, hardware-specific transpilers provided by the vendors are used. The NISQ Analyzer is designed as a plug-in based system, such that additional criteria, e.g., error rates, fidelity, or qubit connectivity, can be added in the future.

Quantum Computers and NISQ . Instead of calculating with classical bits, quantum computers are calculating based on so-called qubits. As classical bits can only be in one of the two states 0 or 1, qubits can be in both states at the same time. The state of a qubit is represented as a unit vector in a two-dimensional complex vector space, and operators that are applied to these vectors are unitary matrices. Qubits interact with their environment, and thus, their states are only stable for a certain time, called decoherence time. The required operations have to be applied in this time frame to obtain proper results from computations. Furthermore, different quantum computing models exist, e.g., one-way, adiabatic, and gate-based. In this book, we only consider the gate-base quantum computing model, as many of the existing quantum computers, e.g., from IBM and Rigetti, are based on this model. In this model, unitary operations are represented as gates, combined with qubits and measurements they form a quantum circuit. Such quantum circuits are gate-based representations of quantum algorithms. The number of gate collections to be executed sequentially is defined as the depth of a quantum circuit. Within such a collection, called layer, gates are performed in parallel. The number of qubits is defined as the width of the circuit. Both properties determine the required number of qubits and the stable execution time of a suitable quantum computer.

Each quantum computer has a set of physically implemented gates. However, the sets of implemented gates differ from quantum computer to quantum computer. Thus, to create quantum circuits for specific problems, gates that are not implemented on the specific quantum computer must be realized by a combination of available gates. This is done by the hardware-specific transpiler of the vendor. Therefore, the transplier maps the gates and qubits of the circuit to the gate sets and qubits of the regarded quantum computers. The resulting transpiled circuit may have a different depth and width than the general circuit. Especially the depth can differ greatly between different quantum computers.

In present time quantum computers only have a small number of qubits and short decoherence times. Further, high error rates limit the number of operations that can be executed on these quantum computers before the propagated error make the computation too erroneous. However, it is assumed that quantum computers will have up to a few hundred qubits and can perform thousands of operations reliably soon. But the limitation is that these qubits will still be error-prone because for the correction of such errors many more qubits are needed. Thus, these quantum computers are also called NISQ machines.

There are a variety of quantum computers that are different regarding their number of qubits, their decoherence time, and their set of physically implemented gates. Therefore, there is serious heterogeneity of available quantum computers, and not every implementation can be executed on every quantum computer.

Quantum Algorithms and Implementations . Many quantum algorithms show a theoretical speedup over their best-known classical counterparts. The number of required qubits and operations for the execution of quantum algorithms often depends on the input data. E.g., the Shor algorithm requires 2n qubits for the integer N with a binary size of n to be factorized. For some implementations, additional qubits are required for executing the algorithm. E.g., QPE, which can be applied to compute the eigenvalues of a unitary matrix, needs in many of the existing implementations additional qubits which define the precision of the result. There are also implementations that can only process a limited input size, e.g., an implementation of Shor that can only factorize up to 15, but may require fewer operations than general, unlimited implementations. Thus, selecting an appropriate quantum computer to execute a certain quantum algorithm not only depends on the mathematics of execute a certain quantum algorithm not only depends on the mathematics of the algorithm itself but also on the physical requirements of its implementations.

In addition, current implementations of quantum algorithms are tightly coupled to the SDKs they are developed with. Companies like IBM and Rigetti offer their proprietary SDKs for their quantum computers, called Qiskit and Forest, respectively. There are also other SDKs that support the quantum computers of multiple vendors, e.g., ProjectQ or XACC. Nonetheless, most of the SDKs only support quantum computers of a single vendor as backends. Furthermore, implementations are not interchangeable between different SDKs because of their different programming languages and syntax. As a result, the majority of the developed implementations are only executable on a certain set of quantum computers provided by a specific vendor.

An implementation of a quantum algorithm implies physical requirements on a quantum computer. In addition, an implementation usually depends on the used SDR. We can summarize the challenges presented before and formulate the research question regarding the selection of quantum computers capable of executing a quantum algorithm for certain input data. For this purpose, the user has to consider different aspects regarding available quantum algorithm implementations and quantum computers. First, it has to manually find a suitable implementation for the required quantum algorithm, which can process the desired input. With the chosen quantum algorithm implementation, the user has to select a suitable quantum computer, that can be used to execute the implementation.

Thereby, the heterogeneity of the quantum hardware, with their different qubit counts, decoherence times, and available gate sets, has to be taken into account. Additionally, the mathematical and technical requirements on the quantum computer and the utilized SDK of the implementation have to be considered for the quantum computer selection. Thus, the selection of implementations and suitable quantum computers requires an immense manual effort and sufficient knowledge on the user side. Hence, the resulting research question can be formulated as follows:

”How can the selection of the quantum algorithm implementation and the suitable quantum hardware be automated based on the input data of the chosen quantum algorithm?”

Example: Quantum computing with neutral atoms. The level of control that has been achieved at the single particle level within 2D and 3D arrays of optical traps, while preserving the fundamental properties of quantum matter (coherence, entanglement, superposition), makes these technologies prime candidates to implement disruptive computation paradigms. In the technological strategy of Pasqal, as example, a startup developing such quantum processors to tackle some of the world's most challenging problems. It was presented the full quantum stack, from atoms / qubits to application interfaces, and propose a classification of a wide variety of tasks that can already be addressed in a computationally efficient manner in the Noisy Intermediate State Quantum era we are in. It was illustrated how applications ranging from optimization challenges to simulation of quantum systems can be explored either at the digital level (programming gatebased circuits) or at the analog level (programming Hamiltonian sequences). We give evidence of the intrin- sic scalability of Pasqal's technology in the 100-1,000 qubits range and introduce prospects for universal fault tolerant quantum computing and applications beyond quantum computing.

The emergence of quantum devices with a few hundred physical qubits (i.e. not error-corrected) opens many exciting perspectives in quantum computing and quantum simulation towards quantum advantage with respect to supercomputers. Among other platforms, fully programmable neutral atom devices display unique characteristics. By controlling quantum entanglement and superposition, either with quantum gates in the digital configuration or with Hamiltonians in the analog configuration, they represent a powerful tool to tackle scientific problems and computing challenges. We explicitly illustrated in the preceding sections how a wide variety of fields will be impacted by the advent of quantum-accelerated computing. We also showed the prospects for future developments at the hardware level, that will allow us to reach the 100 - 1,000 qubits range, and even beyond. In the longer term, neutral atom platforms exhibit many interesting features to push further their computational power and develop new applications. One first appealing direction will be to couple together several Pasqal processors with optical interconnects. This multi-core architecture would then allow us to substantially scale up the number of qubits available for computation. Not only will the increase of the number of physical qubits allow for the exploration of more industry-relevant use cases, but it will also make possible the implementation of quantum error correcting codes such as the surface code on large system sizes. This is one first possible path for the construction of a general-purpose fault-tolerant quantum computing device with neutral atoms. Coupling together distinct Pasqal processors will require to build coherent interfaces between atomic qubits and single photons, which in itself constitutes a great experimental challenge. But developing such an efficient interfacing between individual Pasqal processors and the outer world will also unlock other development avenues.

One application of reliable light-matter interfacing consists in using the atomic ensemble as a quantum memory for a photonic qubit. In that framework, quantum information encoded in an incoming photon can be stored in the atomic medium using the phenomenon of electromagnetically-induced transparency (EIT). Under EIT conditions, an atomic ensemble becomes transparent to light and a single photon can propagate inside it without losses under the form of a mixed light-matter excitation called a polariton. The polariton velocity is greatly reduced as compared to the speed of light in vacuum, and can even be temporarily set to zero, transforming then the atomic ensemble into a quantum memory. Such a quantum memory could be used for the distribution of quantum information over large distances, which represents a great challenge due to photon loss. Several so-called quantum repeater protocols based on atomic ensemble memories have been proposed to overcome this challenge, and experiments are progressing rapidly.

In addition, light-matter interfaces could be harnessed to engineer non-linearities between single photons at the single-particle level. This can be done by combining the EIT phenomenon with the strong dipoledipole interactions in Rydberg media. Under EIT conditions, a single photon can propagate without losses through the atomic medium. When a second photon penetrates inside the medium, the strong dipole-dipole interaction between the atomic components of the two polaritons will result in an effective interaction between the two photons. Such processes constitute a powerful resource for photonic quantum information processing, where quantum logic is applied between photonic quantum bits. In this area of Rydberg nonlinear optics, the Rydberg atoms are no longer the support of the quantum information, but rather act as a source of non-linearity for photonic qubits.

An interesting recent development about photonic quantum computing is the ability to engineer relatively simple error-correction procedures. The infinite dimensional Hilbert space of photons can be used to redundantly encode quantum information, without having to dramatically increase the number of quantum units. Such realizations have also been proposed with superconducting qubits that are used as resources (ancilla) to perform photonic gates in the microwave frequency range. The implementation of such photonic (or bosonic) codes would correspond to a second path towards a fault-tolerant architecture.

As briefly illustrated above, and summarized in Fig. 16, cold neutral atom devices hold great potential for the development of multiple key technologies in the second quantum revolution.

с ф Е Q О

Ф > Ф тз ст с о О) с О

Advanced quantum technologies based _NISq Quantum Processing Unit on atoms

Д Fast classical feedback

Device connectivity

Atom detection i—। Improved set of native operations

4 Noise mitigation

: etc.

Fig. 16. Diagram showing the impact of future technological improvements on (i) the quality of our processors in the NISQ era, and (ii) the development of our future atom-based quantum technologies [7]

In quantum algorithms, computation is described as a sequential application of quantum logic gates onto the qubits. This so-called digital approach to quantum information processing presents several key advantages, such as universality, as any operation can always be re-written with a finite subset of basis gates, and cross-device compatibility. Although the actual implementation of these quantum algorithms is still years away, as they would require ideal digital quantum processors, active research is currently exploring the capabilities of currently available quantum devices, which are imperfect and comprise a relatively modest number of qubits. These devices have recently shown that their computing capabilities can outperform classical supercomputers for a specific computing task. This opens up the so-called Noisy Intermediate Scale Quantum (NISQ) computing era, where 50-1,000 qubits devices allow for the exploration of the entanglement frontier, beyond what classical computers can do. In order to build a viable quantum processor, a broad variety of physical platforms are currently being investigated. Among them, arrays of single neutral atoms manipulated by light beams appear as a very powerful and scalable technology to manipulate quantum registers with up to a few thousands of qubits. In such quantum processors, each qubit is encoded into two electronic states of an atom. Nature provides that all the qubits are strictly identical when taken independently, as opposed to artifical atoms such as superconducting circuits or Silicon spin qubits that need to be manufactured with as little heterogeneity as possible. This feature is a remarkable advantage for neutral atom quantum processors to achieve low error rates during the computation. Atomic devices present other clear advantages with respect to other platforms, such as a large connectivity and the ability to natively realize multi-qubit gates.

In addition to the digital mode where the time evolution of qubits is described by quantum gates, control over the device can be realized at the so-called analog level, where the user can directly manipulate the mathematical operator (the Hamiltonian) describing the evolution of the ensemble of atoms. Not only does it allow for a finer level of control over pulses during the application of gates, but it also makes it possible to directly use the Hamiltonian of the system as a resource for computation. The fine level of control allowed by this analog setting, together with the large number of possible configurations, makes it a powerful tool for quantum processing.

Fundamental research on quantum information processing platforms using neutral atoms has been going on for years, and has led to impressive scientific results such as the simulation of highly complex quantum systems well above 100 qubits, beyond the reach of classical high-performance computers. Only recently did it become possible to contemplate manufacturing devices for commercial use thanks to continuous progress in design and engineering. The company Pasqal has been created in 2019 to leverage the technology developed at Institut d’Optique by the team of A. Browaeys and T. Lahaye in an academic setting precisely for the purpose of building fully programmable Quantum Processing Units (QPUs) for practical quantum advantage for customers.

Such a powerful machine can already bring value to several different fields, which will be described in top block of Fig. 17. For the digital control, we will provide access through all the major frameworks for digital quantum information processing (Qiskit, Cirq, Braket, Myqlm, QuTip etc.), allowing the users to leverage existing hardware-agnostic software tools for applications. For the analog control, we will additionally build a web-based graphical user interface for easy and interactive programming of experiments. In both cases, users will be provided with a precise control over the device dynamics. In the NISQ era, software and hardware development come by pair, therefore some specific software tasks will be developed internally, allowing us to unlock the full potential of Pasqal devices.

Fig. 17. Pasqal quantum stack and metrics to evaluate the performances of the quantum processor

[Applications (top block of the Quantum stack) can be divided into two groups: Quantum Simulation problems that involve the study of a quantum system, and standard computational problems. To solve these problems, the processor developed at Pasqal can be used in a digital way or in an analog way (middle block of the Quantum stack). The low-level part of the stack corresponds to the physical quantum processor.]

The most promising application is Quantum Simulation, where the quantum processor is used to gain knowledge over a quantum system of interest. As Richard Feynman already pointed out in the last century, it seems natural to use a quantum system as a computational resource for quantum problems. Pure science discovery will benefit from Pasqal processors, and fields of applications are numerous at the industrial level, including for example the engineering of new materials for energy storage and transport, or chemistry calculations for drug discovery. Beyond quantum simulation, Pasqal devices can also be used to solve hard computational problems, that cannot be efficiently solved on classical devices. Applications of NISQ computing notably encompass finding approximate solutions to hard combinatorial optimization problems, or enhancing the performances of Machine Learning procedures.

Prospective users will have two distinct ways to explore these applications with Pasqal devices, either at the digital level (programming gate-based circuits) or at the analog level (programming Hamiltonian sequences), as illustrated in the middle block of Fig. 17. For the digital control, we will provide access through all the major frameworks for digital quantum information processing (Qiskit, Cirq, Braket, Myqlm, QuTip etc.), allowing the users to leverage existing hardware-agnostic software tools for applications. For the analog control, we will additionally build a web-based graphical user interface for easy and interactive programming of experiments. In both cases, users will be provided with a precise control over the device dynamics. In the NISQ era, software and hardware development come by pair, therefore some specific software tasks will be developed internally, allowing us to unlock the full potential of Pasqal devices. In addition, electronic controls are needed to tune the light properties, apply instructions arising from the quantum software stack and extract information through atomic detection, as illustrated in Fig. 18.

Fig. 18. Schematic of the hardware components of the Pasqal device

[The user sends, through the quantum software stack, instructions to the register actuators, which initialize the quantum register, and to the processing actuators, which perform the computation. Information in the quantum register is extracted through detection of an image. It serves as an input for real-time rearranging of the register and as an output of the computation.]

The Pasqal Quantum Processing Unit (QPU) is able to implement both digital and analog quantum processing tasks. In digital computing, quantum algorithms are decomposed into a succession of quantum logic gates, described by a quantum circuit as shown in Fig. 19 (a).

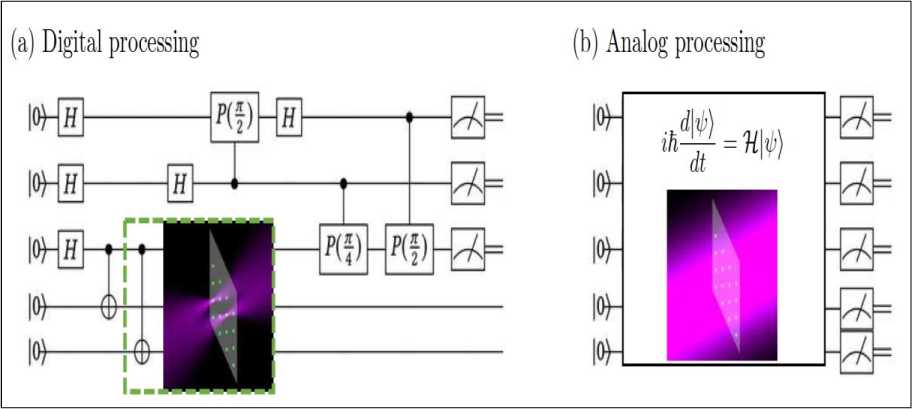
Fig. 19. Digital- vs analog processing. (a) In digital processing, a succession of gates is applied to the qubits to implement a quantum algorithm. Each gate is performed by addressing the qubits individually with laser beams. (b) In analog processing the qubits evolve under a tailored Hamiltonian н , for instance by illuminating the whole register with a laser beam. The wavefunction ψ of the system follows the chrodinger equation

The quantum gates are realized by shining ne-tuned laser pulses onto a chosen subset of individual atoms in the register. In analog computing, lasers are applied to realize Hamiltonian. The qubits evolve in time according to the Schrodinger equation, as illustrated in Fig. 19(b). The final state of the system is probed by measuring the state of each individual qubits.

Figure 20 depicts an overview of the approach for a NISQ Analyzer, which enables an automated analysis and selection of algorithm implementations and quantum hardware depending on the chosen quantum algorithm and specific input data.

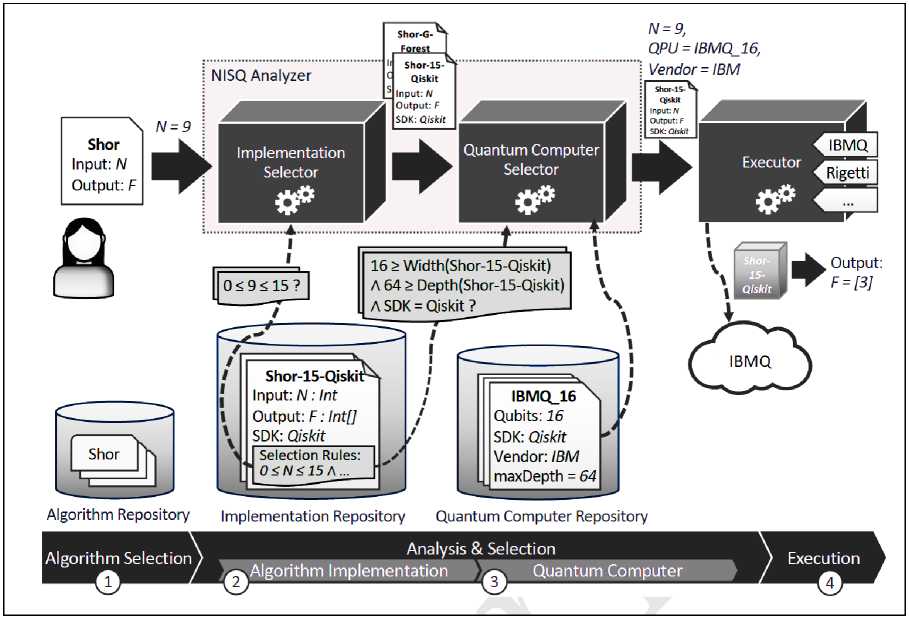
Fig. 20. Approach for automated implementation and quantum hardware selection. [adapted from Marie Salm et al. A roadmap for automating the selection of quantum computers for quantum algorithms // arXiv:2003.13409v1 [quant-ph] 30 Mar 2020]

In the example in Fig. 20 IBMQ-16 can execute Shor-15-Qiskit. In the step (4) Execution phase, the selected implementation is finally executed by the selected quantum computer, as seen in Fig. 20. The Executor supports the different SDKs and can be extended by further plug-ins. Thereby, the required SDK, e.g. Qiskit, is used to deliver the quantum circuit to the specific vendor via the cloud. Eventually, the result is returned and displayed to the user.

The NISQ Analyzer analyzes and selects for a chosen quantum algorithm and specific input data (i) an appropriate algorithm implementation and (ii) a suitable quantum computer, the implementation can be executed on, by means of defined selection rules. Thereby, the width and depth of the algorithm implementations are dynamically determined using hardware-specific transpilers and compared with the properties of available quantum computers. Since quantum computers and implementations are tightly coupled to their SDKs, the compatibility between the SDK used for the implementation and the SDK supported by the quantum computer has to be considered. The selected implementation is then sent to the corresponding vendor of the selected quantum computer.

The PQC is known as a black-box model with tunable parameters associated with layered one qubit or two-qubit quantum gates. Physically, the assigned two-qubit gates may have to be realized through a series of intermediate operations (e.g., SWAP) due to the lack of direct interactions between the target qubits. Thus, the actual complied quantum circuit is usually deeper than the designed circuit.

Today’s quantum computers first, are noisy, i.e. their qubits are erroneous, meaning that their actual states are not stable: the states decay over short periods of time. Similarly, the implementations of the gates used to manipulate the qubits are erroneous to, i.e. a gate does not manipulate the qubits it operates on exactly, resulting in small deviations from the expected result, and such errors propagate in course of the execution of an algorithm. The phenomenon that qubits are erroneous is referred to as decoherence, the phenomenon that gates are erroneous is referred to as gate infidelity. Second, todays industrial technologies of building quantum computers prohibit large numbers of qubits on a device: many qubits on a single device as well as the technology to control and connect them introduce disturbances of the qubits.

Thus, today’s technology has limited scalability, it is of intermediate scale only. Being noisy and of intermediate scale coined the term Noisy Intermediate Scale Quantum (NISQ) computers.

The Impact of Hardware on Quantum Algorithms. Because of noise and the limited number of qubits of NISQ machines, the depth d of a quantum algorithm as well as its width w must be controlled. In practice, the following simple formula results in a rule-of-thumb that is very helpful to assess the limits of executing a quantum algorithm on a given quantum computer: d⋅ w 1 . In this formula ε is the error rate of the quantum computer. Informally, the error rate subsumes decoherence times of qubits, precision and error frequency of gates etc. As implied by the formula, the depth d or the width w have to be “small”. For example, if an algorithm requires 50 qubits (w=50) and it should run on a quantum computer with an error rate of about 10-3 (ε ≈ 10-3), then d must be (significantly) less than 20 (d ≪ 20), i.e. the algorithm has to complete after at most 20 sequential steps - otherwise the result would be much to imprecise. Algorithms that require “few” qubits only can be simulated on classical computers. N qubits imply to store 2N amplitudes of the state of the corresponding N qubit quantum register. As a simplistic estimation (one byte for each amplitude) 2N bytes are needed to store the quantum state of N qubits. Thus, for 20 qubits 220 = (210)2 ≳ (103)2 = 106 bytes are required, i.e. the corresponding quantum state will fit into the main memory of most computers, while for 50 qubits 250 ≳ 1015 bytes are required which is hard even for large supercomputers today (although in special situations a little higher number of qubits can be simulated). Thus, quantum algorithms that are able to prove the power of quantum computers will make use of many qubits because otherwise these algorithms can be simulated on classical computers. According to the formula above, such an algorithm must have a low depth, and the algorithm is then called a shallow algorithm. But if an algorithm requires a high depth (a so-called deep algorithm) it can make use of a few qubits only and it can, thus, be simulated. This implies that quantum advantage has to be shown based on shallow algorithms, i.e. algorithms that use only “a few” layers of parallel gates.The low depth of shallow algorithms implied by the capabilities of today’s NISQ machines mandate to realize hybrid algorithms, i.e. algorithms that are split into classical parts and shallow quantum parts. The classical parts and quantum parts of a hybrid algorithm are performed in a loop where results are optimized from iteration to iteration. Optimization may affect both, the quantum parts of a hybrid algorithm as well as its classical parts.

Figure 21 shows the general structure of a hybrid algorithm (dashed elements indicate optionality).

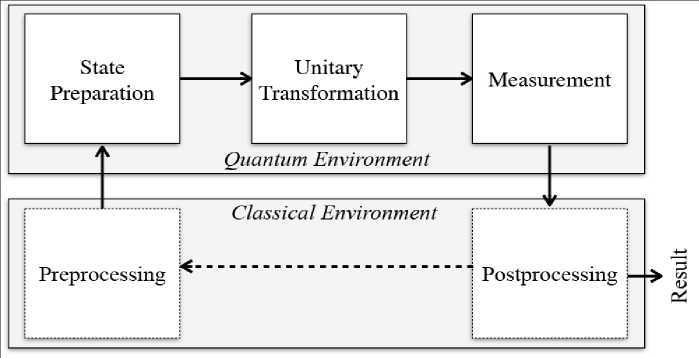
Fig. 21. General structure of a quantum algorithm

Its quantum part is structured like any quantum algorithm: it prepares the state to be manipulated by the unitary transformation representing the algorithm proper, and the result produced by the unitary transformation is measured and passed to the classical environment. If the measured result is satisfiable (e.g. it has a certain precision) it is delivered as the final result. Otherwise the measured result is postprocessed (e.g. parameters that are used to influence the creation of the quantum state are modified), and the output of the postprocessing is passed as input to a preprocessing step that controls the state preparation accordingly.

This structure of a hybrid algorithm is also the generic, principle structure of most quantum algorithms: the quantum state processed by the algorithm proper (i.e. the unitary transformation) must be prepared which typically requires classical preprocessing. The output produced by measuring the result of the algorithm proper must be postprocessed, e.g. by assessing or improving its quality. In many cases the postprocessing step will not kickoff another iteration, i.e. it will not pass input to the preprocessing step (this optionality is indicated in the figure by the dashed format of the arrow between post- and preprocessing). As a consequence, analyzing the unitary transformation, i.e. the algorithm proper is by far not enough for assessing whether or not an algorithm can be successfully executed on a NISQ device. State preparation (tightly interwoven with preprocessing) as well as measurement (tightly interwoven with postprocessing) must be considered to fully understand the requirements of an algorithm and to determine the depth and width of the circuit finally to be executed. Also, the algorithm proper must be analyzed, e.g. if it makes use of oracles: these subroutines contribute themselves to the depth and width of the overall circuit to be performed. The target machine on which the circuit implementing the algorithm should run has its impact on the overall circuit to be executed because it might support a different gate set than assumed by the algorithm or because the target machine reveals certain hardware restrictions.

The three high-level contributions are (i) to raise awareness of developers of quantum software in practice about the fact that the unitary transformation at the core of an algorithm (which is often the focus of its potential users) is not sufficient to assess its successful executability on a certain NISQ machine, (ii) to discuss the main sources of complexity increase of an algorithm when preparing it for execution on a certain NISQ machine, and (iii) to present details about tasks that have to be performed to transform an algorithm into a circuit ready to be executed on a NISQ machine. The need for these contributions has been triggered by work on using quantum algorithms in the humanities: We are working on a component that analyses quantum algorithms and evaluates their fit for certain NISQ machines. It is developing a platform [as part of the PlanQK project that includes the before-mentioned analysis component. Also, it works on a pattern language for quantum computing to support practitioners in developing (hybrid) quantum applications and what it describes in this contribution will result in several extensions of this pattern language.

The goal of provenance is to increase understandability, reproducibility, and quality of the end product or its production process. Provenance provides all the information that supports (i) the assessment of the appropriateness of a particular quantum device for successfully executing a circuit, or (ii) the transformation of a quantum algorithm into a circuit (or even a hybrid algorithm) that delivers acceptable results on a particular quantum device (or even in a hybrid environment). For this purpose, lots of information is needed.

First, information about the circuit implementing an algorithm in a hardware-independent manner must be available, like its gates used, its depth and width. Also, the results of the hardware-dependent transpilation process has to be made available. This information is either derived by inspecting the original circuit itself, or is made available on IBM’s devices as output of the transpiler. Second, information about the potential target quantum devices like their number of available qubits is important, their connectivity, the gate set physically supported by a given machine etc. Beyond this static information also dynamic values like the decoherence times of the qubits, the error rates of single qubit operations and two qubit operations, the error rate of the connections between any two qubits etc is key. This information can be directly retrieved from the devices provided by IBM Quantum Experience, for example. Finally, information subsuming or aggregating, respectively, the processing power of quantum devices is helpful provenance information. For this purpose, different metrics to specify or assess the capability of a quantum computer have been proposed (e.g. quantum volume, total quantum factor).

All this information has to be retrieved and made available for transforming or assessing circuits in a uniform manner across vendors of quantum devices and quantum algorithms. Thus, provenance results in a corresponding database containing static information as well as dynamic information that supports the assessment and transformation of circuits.

Provenance it needed as a basis for assessing and transforming quantum circuits properly. Part of this information can be determined in a one-time effort like static information about a circuit (e.g. its depth), other parts must be regularly provided like dynamic information about a quantum device (e.g. its calibration matrix).

Figure 22 depicts a simplistic architecture of a corresponding provenance system.

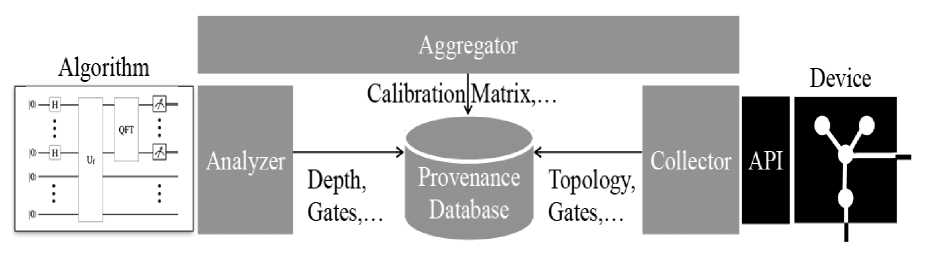
Fig. 22. Capturing provenance information

An analyzer parses algorithms or circuits, respectively, to derive information about the gates used, depth, width etc. A collector component uses APIs available in quantum environments to retrieve information about the topology of quantum devices, the gates directly supported by the hardware, transpiled circuits etc. An aggregator determines the calibration matrix of a quantum device.

Implementing a quantum algorithm on a NISQ device has several challenges that arise from the fact that such devices are noisy and have limited quantum resources. Thus, various factors contributing to the depth and width as well as to the noise of an implementation of an algorithm must be understood in order to assess whether an implementation will execute successfully on a given NISQ device. State preparation, oracle expansion, connectivity, circuit rewriting, and readout: these factors are very often ignored when presenting an algorithm but they are crucial when implementing such an algorithm on near-term quantum computers. This contribution will help developers in charge of realizing algorithms on such machines in (i) achieving an executable implementation, and (ii) assessing the success of their implementation on a given machine.

Its quantum part is structured like any quantum algorithm: it prepares the state to be manipulated by the unitary transformation representing the algorithm proper, and the result produced by the unitary transformation is measured and passed to the classical environment.

Example: A Portable Quantum Programming Framework for Quantum Accelerators (OpenQL). With the potential of quantum algorithms to solve intractable classical problems, quantum computing is rapidly evolving and more algorithms are being developed and optimized. Expressing these quantum algorithms using a high-level language and making them executable on a quantum processor while abstracting away hardware details is a challenging task. Firstly, a quantum programming language should provide an intuitive programming interface to describe those algorithms. Then a compiler has to transform the program into a quantum circuit, optimize it and map it to the target quantum processor respecting the hardware constraints such as the supported quantum operations, the qubit connectivity, and the control electronics limitations. For this purpose is proposed a quantum programming frame work named OpenQL, which includes a high-level quantum programming language and its associated quantum compiler. The programming interface of OpenQL describe the different layers of the compiler and it can provide portability over different qubit technologies. Experiments show that OpenQL allows the execution of the same high-level algorithm on two different qubit technologies, namely superconducting qubits and Si-Spin qubits. Besides the executable code, OpenQL also produces an intermediate quantum assembly code (cQASM), which is technology-independent and can be simulated using the QX simulator.

Example : A Portable Quantum Programming Framework for Quantum Accelerators (OpenQL). In the absence of a fully programmable quantum computer, the implementation of quantum algorithms on real quantum processors is a tedious task for the algorithm designer, especially in the absence of deep expertise in qubit control electronics. In order to make a quantum computer programmable and more accessible to quantum algorithm designers similarly to classical computers, several software and hardware layers are required: at the highest level, an intuitive quantum programming language is needed to allow the programmer to express the quantum algorithm without worrying about the hardware details. Then, a compiler transforms the algorithm into a quantum circuit and maps and optimizes it for a given quantum processor. Ultimately, the compiler produces an executable code which can be executed on the target micro-architecture controlling the qubits. A modular quantum compiler would ideally not expose low-level hardware details and its constraints to the programmer to allow portability of the algorithm over a wide range of quantum processors and qubit technologies. OpenQL1 is an open-source high level quantum programming framework. OpenQL is mainly composed of a quantum programming interface for implementing quantum algorithms independently from the target platform, and a compiler which can compile the algorithm into executable code for various target platforms and qubit technologies such as superconducting qubits and semiconducting qubits. OpenQL has some common characteristics with the early developed compilers, such as being an open-source, modular quantum compilation framework that is capable of targeting different hardware backends. However, the distinctive and, at the same time, the primary motivation behind OpenQL is that it is a generic and flexible compiler framework. These requirements directly translated into the OpenQL design to support multiple configurable backends through its platform configuration file. Finally, OpenQL is one of the engines behind QuTech’s Quantum Inspire platform, where the user can gain access to various technologies to perform quantum experiments enabled through the use of OpenQL’s plugin able backends and its ability to generate executable code.

Quantum Accelerator Model

Accelerators are used in classical computers to speed up specific types of computation that can take advantage of the execution capabilities of the accelerator such as massive parallelism, vectorization or fast digital signal processing. OpenQL adopts this heterogeneous computing model while using the quantum processor as an accelerator and provides a programming interface for implementing quantum algorithms involving both classical computation and quantum computation. Heterogeneous computing is a computing model where a program is executed jointly on a general-purpose processor or host processor and an accelerator or co-processor. The general-purpose processor is capable of executing not only general computations such as arithmetic, logic or floating point operations, but also controlling various accelerators or coprocessors. The accelerators or co-processors are specialized processors designed to accelerate specific types of computation such as graphic processing, digital signal processing and other workloads that can take advantage of vectorization or massive thread-level parallelism. Therefore, the accelerator can speedup a part of the computation traditionally executed on a general-purpose processor. The computation is then offloaded to the accelerator to speed up the overall execution of the target program. Examples of accelerators are the Intel Xeon Phi coprocessor, Digital Signal Processors (DSP), Field Programmable Gate Array (FPGA) that can be also utilized as accelerators to parallelize computations and speed up their execution. Finally, GeneralPurpose Computation on Graphics Processing Units (GPGPU) uses GPU as accelerator to speed up certain types of computations.

Quantum Processors as Accelerators . The OpenQL programming framework follows a heterogeneous programming model which aims to use the quantum processor as a co-processor to accelerate the part of the computation which can benefit from the quantum speedup. A quantum algorithm is generally composed of classical and quantum computations. For instance, Shor’s algorithm is a famous quantum algorithm for prime number factoring; as shown in Fig. 23 the algorithm includes classical computations such as the Greatest Common Divisor (GCD) computation which can be executed efficiently in a traditional processor, and a quantum part such as the Quantum Fourier Transform which should be executed on a quantum processor.

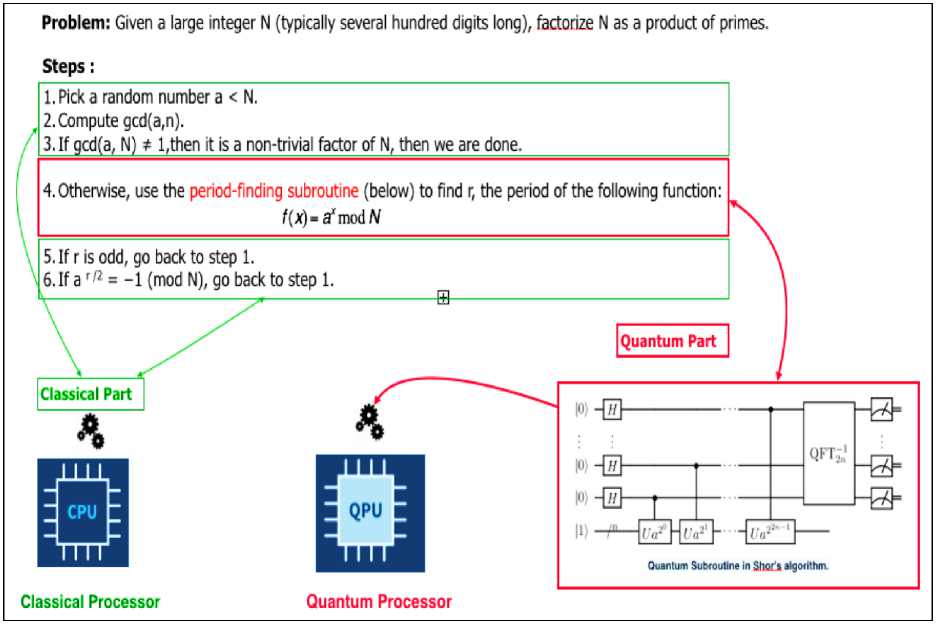
Fig. 22. Shor’s algorithm is composed of both classical computations and quantum computations

OpenQL uses traditional host languages, namely C++ and Python, to define a programming interface which allows the expression of the quantum computation and the communication with the quantum accelerator: the quantum operations are executed on the quantum processor using a dedicated micro-architecture and the measurement results are collected and sent back to the host program running on the classical processor. While non time-critical classical operations can be executed on the host processor, time-critical classical operations that need to be executed within the coherence time of the qubits, such as in error correction quantum circuits, can be ofа loaded to the accelerator to provide fast reaction time and avoid communication overhead between the host PC and the accelerator.

Figure 23 depicts OpenQL framework which exposes a high-level programming interface to the user at the top. The compiler implements a layered architecture which is composed mainly of two parts: a set of hardware-agnostic compilation passes that operate at the quantum gate level, and a set of low-level technology specific backends which can target different quantum processors with specific control hardware. The goal of those backends is to enable compiling the same quantum algorithm for a specific qubit technology without any change in the high-level code and making the hardware details transparent to the programmer. Moreover, this architecture allows the implementation of new backends to extend the support to other qubit technologies and new control hardware whenever needed.

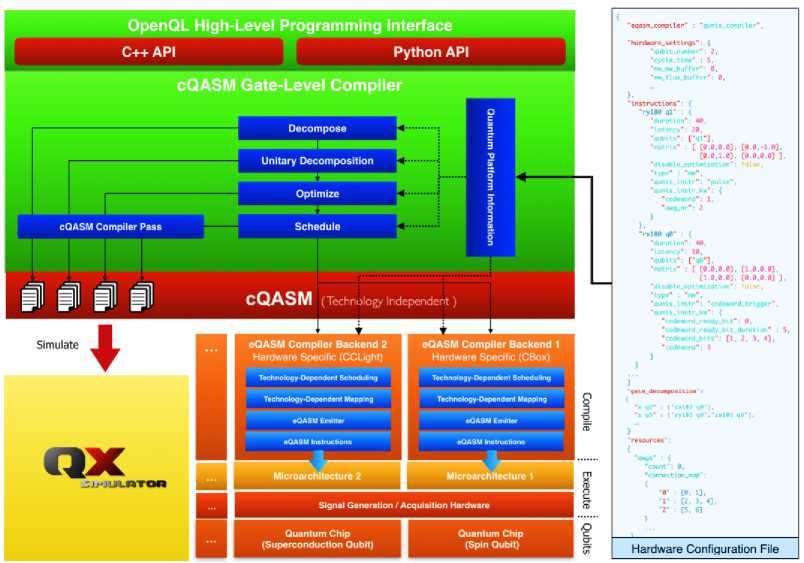
Fig. 23. OpenQL Compiler Architecture [11]

As the qubit control hardware is constantly evolving in the last years, this flexibility and portability over a wide range of hardware is crucial. This enhances the productivity and ensures the continuity of the research efforts towards a full-stack quantum computer integration.

The Quantum Assembly Language (QASM) is the intermediate layer which draws the abstraction line between the high-level hardware-agnostic layers (gate-level compilation stages) and the low-level hardware specific layers. The low-level layers are implemented inside a set of interchangeable backends each targeting a different microarchitecture and/or a different qubit technology.

The OpenQL framework is composed mainly of the following layers:

• -    A High-level programming interface using a standard host language namely C++ or Python to express the target quantum algorithm as a quantum program.

• -    A quantum gate-level compiler that transforms the quantum program into a quantum circuit, optimizes it, schedules it and maps it to the target quantum processor to comply to the different hardware constraints such as the limited qubit connectivity.

• -    The last stage of the gate-level compilation produces a technology-independent Common Quantum Assembly code (cQASM) which describes the final quantum circuit while abstracting away the low-level hardware details such as the target instruction set architecture, or the quantum gate implementation which differ across the different qubit technologies For now, our compiler targets Superconducting qubits and Si-Spin qubits but can be easily extended to other qubit technologies. The produced QASM code complies with the Common QASM 1.0 syntax and can be simulated in our QX simulator to debug the quantum algorithm and evaluate its performance for different quantum error rates.

• -    At the lowest level, different eQASM (executable QASM) backends can be used to compile the QASM code into instructions which can be executed on a specific micro-architecture, e.g. the QuMA micro-architecture. At this compilation level, very detailed information about the target hardware setup, stored in a hardware configuration file, is used to generate an executable code which takes into account various hardware details such as the implementation of the quantum gates, the connectivity between the qubits and the control instruments, the hardware resource dependencies, the quantum operation latencies and the operational constraints.

OpenQL provides three main interfaces to the developer, namely Quantum Kernel, Quantum Program and Quantum Platform.

Quantum Kernel. A Quantum Kernel is a quantum functional block which consists of a set of quantum or classical instructions and performs a specific quantum operation. For instance, the kernel could be dedicated to creating a bell pair while another could be dedicated to teleportation or decoding. OpenQL supports standard quantum operations. To allow for further flexibility in implementing the quantum algorithms, custom operations can also be defined in a hardware configuration file. These operations can either be independent physical quantum operations supported by the target hardware or a composition of a set of physical operations. Once defined in the configuration file of the platform, the new operation can be used in composing a kernel as any other predefined standard operation. This allows for more flexibility when designing a quantum algorithm or a standard experiment used for calibration or other purposes.

Quantum Program . As the quantum kernels implement functional blocks of a given quantum algorithm, a ”quantum program” is the container holding those quantum kernels and implementing the complete quantum algorithm. For instance, if our target algorithm is a quantum error correction circuit which includes the encoding of the logical qubit, the error syndrome measurement, the error correction and finally the decoding, we can create four distinct kernels which implement these four blocks, and it can add these kernels to the program. The program can then be compiled and executed on the target platform.

Quantum Platform. A ”quantum platform” is a specification of the target hardware setup including the quantum processor and its control electronics. The specification includes the description of the supported quantum operations and their attributes such as the duration, the built-in latency of each operation and the mathematical description of the supported quantum operation such as its associated unitary matrix. Therefore, the OpenQL quantum programming framework which includes a high-level quantum programming language and its compiler. A quantum program can be expressed using C++ or Python interface and compiler translates this high-level program into a Common QASM (cQASM) to target simulators. This program can further be compiled for a specific architecture targeting physical quantum computer. OpenQL has been used for implementing several experiments and quantum algorithms on several quantum computer architectures targeting both superconducting and semiconducting qubit technologies.

Quantum supremacy. Quantum supremacy is the goal of demonstrating that a programmable quantum device can solve a problem that classical computers practically cannot. In 2019, Google officially announced that it achieved the milestone of “quantum supremacy”. They performed the random circuit sampling on a programmable superconducting quantum processor with 53 available qubits called Sycamore (see Fig. 24).

Fig. 24. The Sycamore processor. (a) Layout of processor. (b) Photograph of the Sycamore chip

In their work, the improvement of the 2-qubit gate fidelity, and the reduction of cross talks in parallel gate operations are critical techniques for this progress. And finally, they showed a computational experiment that implements an impressively large two-qubit gate quantum circuit of depth 20, with 430 two-qubit and 1,113 single-qubit gates, and with predicted total fidelity of 0.2%.

From circuit model to control model. Let us take a closer look at an experimental superconducting quantum computing system shown in Fig. 25.

Fig. 25. The physical control ow of a hybrid quantum-classical algorithm deployed on a NISQ processor

The arbitrary waveform generator (AWG) produces control pulses that manipulate and measure the qubits on the processor. According to the qubit measurement outcomes, the classical computer runs the training algorithm to instruct the AWG to iteratively updates the control pulses. The controlled quantum evolution forms a quantum neural network (NN) parameterized by the time-dependent AWG parameters.

All gate operations in the PQC must be realized by shaped microwave pulses produced by an arbitrary waveform generator (AWG). These pulses are iteratively adjusted by a classical computer according to the empirical loss evaluated by measuring the control-guided output states. Thus, the entire PQC is in fact dictated by the AWG control pulses, whose amplitudes parameterize a new quantum NN realized by the controlled quantum dynamics. In this way, we can replace the gate-based model by a control-based model.

Interestingly, the control-based model also has a layered feedforward network structure owing to the piecewise-constant characteristic of AWG pulses. Ideally, the steering process of these pulses on the quan-

M.

H о 'E w ( t ) h l^V( t^ , where

tum system can be characterized by the Schrodinger equation: | V ( t )^ = - i

| V ( t )) is the quantum state (starting from an initial state 1| V ( t ₀ )^ = 10) of the entire system, and w i (t)/ • , W m (t) are the amplitudes of the control fields. Each control field consists of M piecewise constant sub-pulses over M sampling periods. The states | V ( t_k )^ at the end of each sub-interval form a layer of the quantum NN, and the control variables denoted by w =[ w ( t_k ),..., w_M ( t_k ) ] , k = 1,..., N , are the equivalent NN hyperparameters as schematically shown in Fig. 25. The depth of the quantum NN is equal to the number of AWG sampling periods during the entire quantum evolution.

The control-based model is a generalization of the gate-based model because any gate operation must be eventually realized through physical control pulses. Comparing with the gate-based PQCs, it is hardware more friendly because all parameters are directly adjustable without having to be artificially split into separate gates. From hand-designed to auto-selected features. In most PQC-based learning models, the data vector is mapped to the quantum state using a pre-selected encoder to represent the set of hand-designed features. As schematically shown in Fig. 26(a), the same strategy can be applied as well in control-based models.

DATA INPUT

control as weights

(a)

Ю)

State Preparation (selected encoder)

I^da ta^ Quantum NN (learning)

LABEL

Fig. 26. Quantum end-to-end learning models that consist of encoding and inference control networks. (a) The data is encoded to the quantum state through a pre-selected encoder; (b) the data is encoded to the quantum state through a data-to-control interface (a classical NN) via a selected set of agent control variables [19]

Effectively manipulating quantum computing hardware in the presence of imperfect devices and control systems is a central challenge in realizing useful quantum computers. Susceptibility to noise in particular limits the performance and algorithmic capabilities experienced by end users. Fortunately, in both the NISQ era and beyond, quantum control enables the efficient execution of quantum logic operations and quantum algorithms exhibiting robustness to errors, without the need for complex logical encoding.

Following the encoding control processes, inference control pulses are applied as weights to infer the class that the input belongs to. The encoder first ‘translates’ the data vector to a quantum state, following which a physical control is applied to prepare the system in this state. The applied control could be very difficult to design when the encoded states are highly entangled (e.g., in the amplitude encoding scheme for exploiting the superposition of quantum states). The scheme also becomes impractical when dealing with large-size datasets because every single sample needs an individually designed control pulse. The `transla-tion' from the data vector to the quantum state can be designed in an implicit and automatic manner. As is shown in Fig. 26(b), we introduce an intermediate data interface (e.g., a layer of classical perceptrons) that transforms the data vector into a selected set of agent control variables. The quantum state steered by these control variables then encodes the in-put data, but the encoded state is not explicitly (and neither necessarily) known unless being recon-structed through tomography. The introduced data-to-control interface is to be trained together with the rest part of the quantum NN, forming a hybrid quantum-classical neural network. The selected encoding control variables act as a hidden layer that passes the input data from the classical computer to the quantum processor. Once the interface is well trained, control pulses will be automatically generated to prepare the target encoded state. In addition, the encoding scheme also brings favored nonlinearity through the nonlinear control-to-state mapping, which potentially leads to better model expressivity in complex learning tasks. A hardware-friendly quantum end-to-end learning model can be easily deployed on NISQ processors. The hybrid quantum-classical model involves quantum neural networks parameterized by experimental addressable control pulses, and an embedded data-to-control interface for automatic feature selection. Numerical tests on the benchmarking MNIST dataset demonstrate that the model can efficiently achieve high performance with only a few qubit on real-world learning tasks without down-sampling the images. Taking into accounts of the precision, the size of dataset, and the model size, the scheme exhibits the best overall performance.

The model turns training process into an optimal control problem, both of which can be resolved with gradient-descent algorithms. This interesting connection between optimal control and machine learning problems can be dated back, where the famous Back Propagation algorithm was derived from foundational Pontryagin Maxi-mum's Principle (PMP) in optimal control theory. Recently, it was rediscovered that PMP can be effectively applied to deep learning, and from the opposite side, the design of robust quantum controls and quantum optimizers can be taken as the design of a generalized learning model.

When considering quantum control in the context of hardware stabilization for qubits in quantum computers, generally presented with three interrelated control-engineering-inspired approaches:

• -    Measurement-free open-loop control

• -    Destructive closed-loop feedback via projective measurements

• -    Indirect closed-loop feedback which preserves quantum coherence via weak measurements or the use of ancillae.

Open-loop control refers to feedback-free actuation on a system, as in the case of a timed irrigation system which can maintain a lawn without information on soil moisture or rainfall. It provides the substantial benefit that it is resource efficient and in the quantum domain has proven to be remarkably effective in stabilizing quantum devices both during free evolution and during nontrivial logic operations. In this framework, quantum logic operations are redefined to provide the same mathematical transformation within the computational space, but in a way that provides robustness against various error-inducing noise processes. The implementation of open-loop quantum control involves temporal modulation of incident control fields employed to enact manipulation of physical devices.

The use of feedback control, in which actuation is determined based on measurements of the system, is highly constrained by the destructive nature of projective measurement in quantum mechanics. While novel control strategies can be developed for predictive control during unsupervised periods, direct destructive measurements on data qubits are not commonly used within quantum computing architectures. These challenges may be mitigated through the use of indirect measurements on embedded sensor ancilla qubits. Such techniques use physically proximal qubits as transducers to detect local noise in the device with actuation on unsupervised data qubits. Weak measurements also provide a means to stabilize data with minimal perturbation to the encoded quantum information, and have seen adoption in superconducting circuits and NV diamond.

Quantum annealing is a practical approach to execute the native instruction set of the adiabatic quantum computation model. The key of running adiabatic algorithms is to maintain a high success probability of evolving the system into the ground state of a problem-encoded Hamiltonian at the end of an annealing schedule. This is typically done by executing the adiabatic algorithm slowly to enforce adiabacity. However, properly optimized annealing schedule can accelerate the computational process. Inspired by the recent success of DeepMind’s AlphaZero algorithm that can efficiently explore and find a good winning strategy from a large combinatorial search with a neural-network-assisted Monte Carlo Tree Search (MCTS), we adopt MCTS and propose a neural-network-enabled version, termed Quantum Zero (QZero), to automate the design of an optimal annealing schedule in a hybrid quantum-classical framework. The flexibility of having neural networks allows us to apply transfer-learning technique to boost QZero’s performance. We find both MCTS and QZero to perform very well in finding excellent annealing schedules even when the annealing time is short in the 3-SAT examples we consider in this study. We also find MCTS and QZero to be more efficient than many other leading reinforcement learning algorithms for the task of desining annealing schedules. In particular, if there is a need to solve a large set of similar problems using a quantum annealer, QZero is the method of choice when the neural networks are first pre-trained with examples solved in the past.

The quantum computing community has also investigated how to take advantage of this powerful artificial intelligence (AI) method to design quantum algorithms. In this section, we introduce the Monte Carlo Tree Search and an enhanced version equipped with neural networks, termed QZero. MCTS aims at finding a vector of discrete variables x ^∗ that maximizes or minimizes a target property f (x)evaluated by a problem-specific learning environment. For designing an annealing schedule, x = { x 1 , x 2 , x 3 ,..., x M }corresponds to coefficients of Fourier series introduced. MCTS performs the search on a M + 1-level tree structure. The zero-th level is just a root node, which denotes a starting point and carries no other significance. Every solution x specifies a path along the tree structure from top to bottom. In Fig. 27, we illustrate how a MCTS search is conducted on a (3 + 1)-level tree composed of 3 nodes in each level. Ignoring the zero-th level, the tree structure actually looks like a 3 by 3 square board shown in the right panel of Fig. 27.

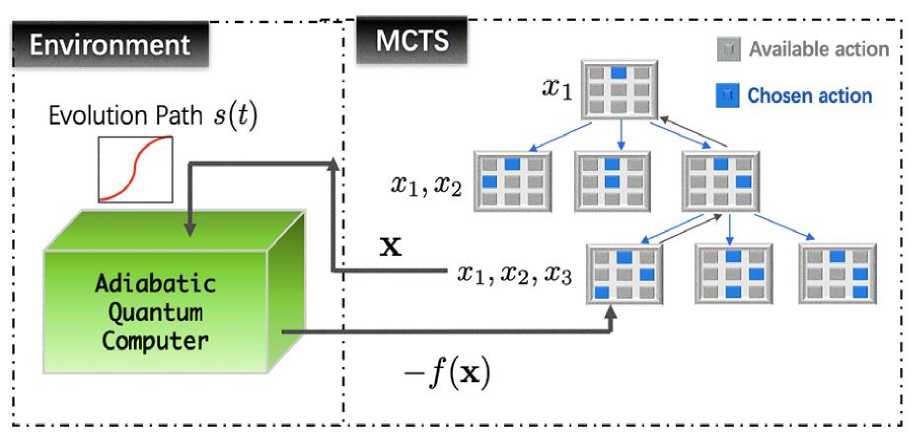
Fig. 27. Setup of MCTS

The MCTS starts at the root and traverses the tree level by level. The algorithm has to select a node (blue-colored box in figure) before proceeding to the next level. As illustrated in the Fig. 27, the MCTS decides a path by sequentially inserting x 1 , x 2 and x 3 into an array specifying the path {},{ x 1 },{ x 1 , x 2 },{ x 1 , x 2 , x 3 }, Each round of MCTS consists of four stages: selection, expansion, simulation and back propagation. In the selection stage, a path is traversed from the root down to a node x k at k -th level by choosing the nodes x i (with I ≤ k ) having maximum Upper Confidence Bound (UCB) score at each level x i = max a u a , where a represent the candidate action nodes in the corresponding level. The UCB score indicates how promising it is to explore the subtree under the current node. While MCTS is an extremely powerful approach to search a large combinatorial space, it is nevertheless a time-consuming procedure; especially, when the space grows exponentially with the number of Fourier components. If one is expected to solve a large set of similar problems, it will be highly desirable that one can utilize experiences in solving similar problems to accelerate the search. One way to achieve this goal is to combine MCTS with neural networks and resort to a host of transfer-learning techniques. In particular, we look up to the design of AlphaZero to introduce both policy and value net-works to enhance search efficiency of MCTS. Furthermore, these neural networks can be straightforwardly pre-trained by learning from past experiences of solving similar problems. Below, we discuss adaptations of the standard AlphaZero to work in the context of quantum annealing, and term it QZero. The following three points highlight the main differences between DeepMind’s AlphaZero and QZero.

Quantum annealer as a learning environment . Quantum annealers are usually used to solve problems under the adiabatic quantum computation (AQC) framework, which relates the solutions of a problem to the ground states of a problem-encoding Hamiltonian H final . Preparing the ground state of an arbitrary Hamiltonian is not a simple task. A common approach is to prepare the ground state of an alternative Hamiltonian H init that we can achieve with high success probability in experiments. Next, we slowly modify a timedependent Hamiltonian H ( s ) , along a pre-defined annealing path, until it morphs into H final at the end. According to the adiabatic theorem, the time-evolved wave function will be highly overlapped with the instantaneous ground state of H ( s ) .

Figure 28 gives an overview of the hybrid quantum-classical programming of a quantum annealer for automated path design.

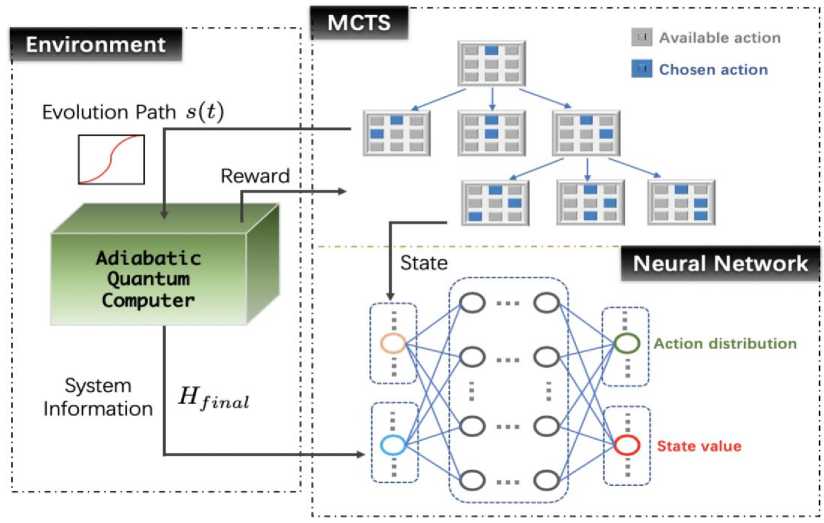
Fig. 28. Hybrid quantum-classical framework for designing annealing schedules. (i) Environment: a quantum annealer executes an annealing schedule encoding a specific problem and provides feedback, upon energy measurement, to a learning agent composed of MCTS and neural networks (for Quantum Zero). (ii) MCTS: the main search component of a learning agent. The search repeats the steps of selection, expansion, simulation and back propagation as introduced in the Method section. (iii) QZero: The self-play of MCTS can be assisted with neural networks, which takes the current path explored by the MCTS as state and system information (the Hfinal) as inputs and gives out action distribution and state values as outputs to guide MCTS. [adapted from Chen Y.-Q. Optimizing quantum annealing schedules: From Monte Carlo tree search to quantum zero // arXiv:2004.02836v1 [quant-ph] 6 Apr 2020)]

Hence, one retrieves the correct solution at the end of the annealing with high probability. More precisely, in each AQC calculation, we need to engineer a time-dependent Hamiltonian,

^H ( s ) = ( 1 - s ) H int + s^H final , s ^G [ 0,1 ]

The process of tuning the Hamiltonian has to be implemented slowly in comparison to the time scale set by the minimal spectral gap of H (s) along the annealing path. Clearly, the time takes to complete an AQC calculation depends crucially on the spectral gap of H (s) . In reality, it is often necessary to finish the calculation within a finite time duration T due to various reasons such as computational efficiency and noise corruptions. This time-limit constraint (on annealing) may violate the adiabatic evolution strictly required by AQC. Nevertheless, one can still run a quantum annealer with some schedule s (t), hoping to reach the ground state of Hfinal. We note this task of optimizing the schedule s (t) may be viewed as an optimal control problem aiming to minimize the energy as the cost function, argminV(T)|Hfmal\y(T)^, where {s(t)}

d

— |V ( t )) = - iH ( s ( t ))| v ( t )) and | v ( 0 ))

is the ground state of Hinit. The optimal control problem is now reduced to assigning values to the sequence x = {x1, x2, x3,..., xM}. MCTS and QZero (an enhanced MCTS boosted with value and policy NNs) to explore the combinatorial search space of all the possible values for x and decide the optimal sequence. The search algorithm is primarily executed on a classical computer; however, the evaluation of a particular annealing schedule x to give us the desired ground state is supposedly performed by a quantum annealer.

The quantum computer promises enormous information storage and processing capacity that can eclipse any possible conventional computer. This stems from quantum entangled superpositions of individual quantum systems, usually expressed as a collection of quantum bits or qubits, whose full description requires exponentially many parameters. However, there are two critical challenges in bringing quantum computers to fruition:

Challenge 1: The vast amount of information contained in massively entangled quantum systems is itself not directly accessible, due to the reduction of quantum superpositions upon measurement. Instead, useful quantum computer algorithms guide a quantum state to a much simpler form to produce some type of global property of the information that can be directly measured. However, the full scope of applications that can exploit entangled superpositions in this way and how exactly quantum computers will be used in the future remains unclear.

Challenge 2: Quantum computers are notoriously difficult to build, requiring extreme isolation of a large number of individual qubits, while also allowing exquisite control of their quantum states and high-accuracy measurements. Quantum computer technology is nothing like classical computer hardware and involves unconventional information carriers in exotic environments like high vacuum or very low temperature. Ultimately, large-scale quantum computers will utilize error-correction techniques that are much more complex than their classical counterparts.

There are several known quantum algorithms that offer various advantages or speedups over classical computing approaches, some even reducing the complexity class of the problem. These algorithms generally proceed by controlling the quantum interference between the components of the underlying entangled superpositions in such a way that only one or relatively few quantum states have a significant amplitude in the end. A subsequent measurement can therefore provide global information on a massive superposition state with significant probability.

The coherent manipulation of quantum states that defines a quantum algorithm can be expressed through different quantum computational modes with varying degrees of tunability and control. The most powerful quantum computing mode presently known is the universal gate model, similar to universal gate models of classical computation. Here, a quantum algorithm is broken down to a sequence of modular quantum operations or gates between individual qubits. There are many universal quantum gate families operating on single and pairwise qubits, akin to the NAND gate family in classical computing. One popular universal quantum gate family is the grouping of two-qubit CNOT gates on every pair of qubits along with rotation gates on every single qubit.

With universal gates, an arbitrary entangled state and thus any quantum algorithm can be expressed. Alternative modes such as measurement-based or cluster-state quantum computing can be shown to be formally equivalent to the universal gate model. Like the NAND gate in classical CMOS technology, the particular choice of universal gate set or even mode of quantum computing is best determined by the quantum hardware itself and its native interactions and available controls. The structure of the algorithm itself may also impact the optimal choice of gate set or quantum computing mode. There are other modes of quantum computation that are not universal, involving subsets of universal gate operations, or certain global gate operations with less control over the entire space of quantum states. These can be useful for specific routines or quantum simulations that may not demand full universality. Although global adiabatic Hamiltonian quantum computing can be made universal in certain cases, it is often better implemented as non-universal subroutines for specific state preparation. Quantum annealing models do not appear to be universal, and there is current debate over the advantage such models can have over classical computation. The gates that explicitly include error, or decoherence processes, used to model quantum computer systems interacting with an environment via quantum simulation.

Conclusions

Software engineering is a problem-solving process with roots in behavioral, engineering, project management, computer science, programming, cost management, and mathematical science. According to Fig. 29, the software engineering process can be defined as follows: "A software process can be defined as the coherent set of policies, organizational structures, technologies, procedures, and artifacts that are needed to conceive, develop, deploy, and maintain a software product." The general requirements for quantum computer hardware are that the physical qubits (or equivalent quantum information carriers) must support (i) coherent Hamiltonian control with sufficient gate expression and fidelity for the application at hand, and (ii) highly efficient initialization and measurement. These seemingly conflicting requirements limit the available physical hardware candidates to just a few at this time. Below we describe those platforms that are currently being built into multi-qubit quantum computer systems and are expected to have the largest impact in the next decade. As we will see below in a definition of levels of the quantum computer stack and a sampling of vertical implementations and applications, the near-term advances in quantum computer science and technology will rely on algorithm designers understanding the intricacies of the quantum hardware, and quantum computer builders understanding the natural structure of algorithms and applications.

Definition and structure of QSE

Jianjun Zhao (2020), Quantum Software Engineering Landscapes and Horizons

Software Engineering (SE) (Friedrich L Bauer):

The establishment and use of sound engineering principles in order to obtain economically software that is reliable and works efficiently on real machines

Nanostructures methods

Nanostructures Quantum algorithms and production for Quantum software,engineering quantum computer

Quantum software engineering (QSE) is the use of sound engineering principles for the development, operation, and maintenance of quantum software and the associated document to obtain economically quantum software that is reliable and works efficiently on quantum computers.

In this definition, we would like to highlight three important issues in QSE.

First, it is important to apply the "sound engineering principles" to quantum software development.

Second, the quantum software should be built "economically," Finally, the quantum software should be "reliable" and needs to work "efficiently" on quantum computers.

Quantum software engineering can be regarded as a branch of systems engineering, which involves the development of large and complex quantum software systems.

V.V. Korenkov, A.G. Reshetnikov, S.V. Ulyanov, Quantum software engineering Pt 3: Quantum supremacy modelling. -M.: Kurs, 2021.

Fig. 29. The definition of soft ware engineering and quantum software engineering

This is where the concept of the proposed Quantum Software Platform (QuSP) comes in [24]. Components of the QuSP and user groups involved are shown in Fig. 30.

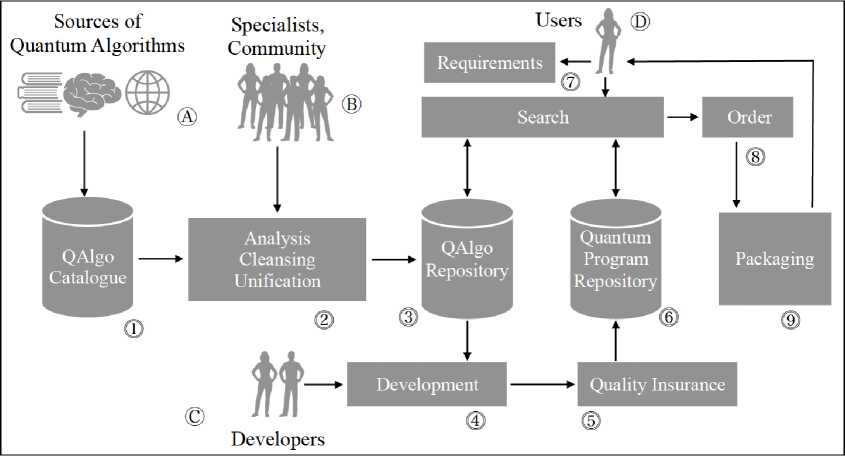
Fig. 30. Architecture of the quantum software platform QuSP

The algorithms for the QuSP come from many different sources (A) (NB: letters and numbers refer to labels in Fig. 30) such as the web, published articles or books. These algorithms are stored in a special database, the quantum algorithm catalog (1). A public community (analogous to an open source community) or specialists of the platform operator (B) can access this special database and analyze, clean and unify the algorithms (2). As a result, each quality-assured algorithm is stored in the Quantum Algorithm Repository (3). Based on the quality-assured algorithms, developers (C) can now implement these algorithms for execution on a quantum computer (4). These programs are also quality-assured (5) and stored in a quantum program repository (6). End users (D) of the platform can now search for quality-assured algorithms and programs in the QuSP (7). If an algorithm for a certain problem is not found or if an algorithm is not implemented by a program, the end user can make corresponding requests (7) to the community. For delivery, an algorithm or program is packaged (9).

Figure 31 shows the life cycle,which encompasses the following phases,each one is flowing into the next.

- Quantum software requirements analysis

-  Quantum software design

-  Quantum software implementation

-  Quantum software testing

-  Quantum software maintenance.

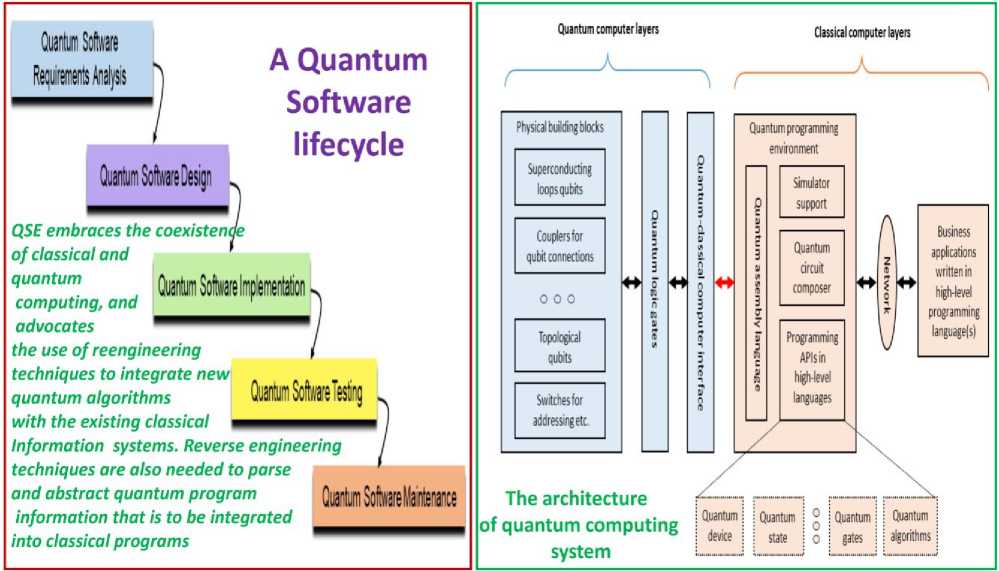
Fig. 31. A quantum software lifecycle and the architecture of quantum computing system

As shown in Fig. 31, the architecture comprises of two parts: quantum layer and classical layer. The quantum layer contains purely quantum hardware and circuitry, and can be considered as comprising the quantum processing unit (QPU). The detailed composition of this layer is listed as follows.

• -    Physical building blocks include quantum hardware that typically makes use of superconducting loops for the physical realization of qubits, and the physical qubit coupler/interconnect circuitry and other elements that are needed for qubit addressing and control operations.

• -    Quantum logic gates contain physical circuitry that makes up quantum logic gates.

• -    Quantum-classical interface includes the hardware and software which provides the interfacing between classical computers and a QPU.

First, the problem is defined at a high-level and based on the nature of the problem a suitable quantum algorithm is chosen. Next, the quantum algorithm is expressed as a quantum circuit which in turn needs to be compiled to a specific quantum gate set. Finally, the quantum circuit is either executed on a quantum processor or simulated with a quantum computer simulator.

Figure 32 demonstrated the visualization of a typical quantum algorithm workflow on a gate-model quantum computer.

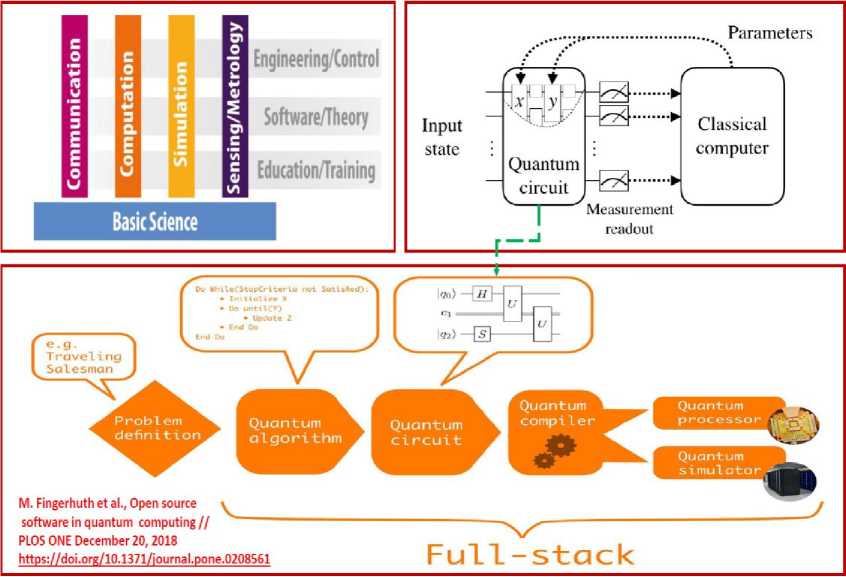
Fig.32. Visualization of a typical quantum algorithm workflow on a gate-model quantum computer

If the scale of the quantum system is still classically simulable, the resulting quantum circuit can be simulated directly with one of the available open source quantum computer simulators on a classical computer. The terminology is confusing, since hardware-based quantum simulators form a quantum computing paradigm as we classified above. Yet, we also often call classical numerical algorithms quantum simulators that model some quantum physical system of interest, for instance, a quantum many-body system. To avoid confusion, we will always use the term quantum computer simulator to reflect that a quantum algorithm is simulated on classical hardware.

As opposed to a quantum computer simulator, the quantum processing unit (QPU) is the actual quantum hardware representing one of the quantum computing paradigms.

Acknowledgments. Long time ago (in Moscow University, 1968) S.V. Ulyanov together with Slava Belavkin and Lev Levitin starting the R&D activity in the background of the quantum control and quantum information (in the group of Ruslan L. Stratonovich with the support from Andrey N. Kolmogorov.) The many years of fruitful and friendship discussions created many ideas and millstone results. Many thanks to our friends and for the mutual support in difficult temporal period of 90’s.

Capri, 2001.

This textbook is dedicated to the Slava’s memory.