Quantum software engineering supremacy in intelligent robotics

This report is concerned with the problem of discovering a new family of quantum algorithms (QA’s). The presented method and relative hardware implements matrix operations performed in second and third step of a QA the so-called interference and entanglement operators), this operators allow you to achieve a substantially increasing in computational speed-up with respect to the corresponding software realization of a traditional and a new quantum search algorithm (QSA). A high-level structure of a generic entanglement block that uses logic gates as analogy elements is described. Moreover, a new method for performing Grover interference without products is introduced. This model has the advantage that proving lower bounds is tractable which allows one to demonstrate provable speed-up over classical algorithms or to show that a given QA is the best possible [1, 2]. Next, we will describe the method of designing main quantum operators and hardware implementation of Grover’s algorithm for fast search in large unstructured database and related topics concerning the intelligent control in robotic of an ill-defined process including search-of-minima entropy uncertainty intelligent operations is described. Quantum supremacy of intelligent robotic control with quantum fuzzy inference demonstrated on Benchmarks.

General Structure of QA

A QA estimates (without numerical computing) the qualitative properties of the function f . From a mathematical standpoint, a function f is the map of one logical state into another. The problem solved by a QA can be stated in the symbolic form as follows:

Input	A function f: {O.iy ^ tO.l} "
Problem	Find a certain property of function f

The general structure of QA on Fig. 1 is demonstrated.

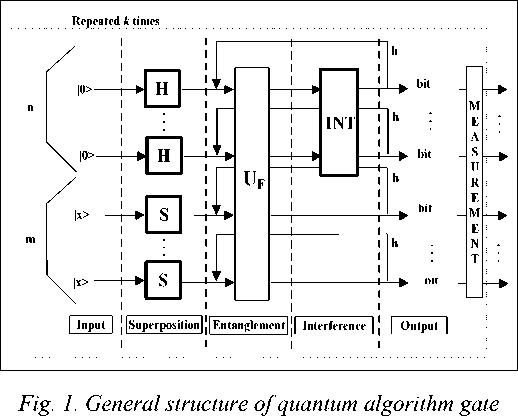
In general, the superposition operator consists of the combination of the tensor products Hadamard H operators with identity operator I :

72 L1

^^^^^^B

, i =

The superposition operator of most QAs can be expressed (see Fig. 1) as following: ( n_V(m

Sp = 1® H | ® I ® S I, where n and m are the numbers of inputs and of outputs respectively. Operator S may V i=1    /     V i=1 / be or Hadamard operator H or identity operator I depending on the algorithm. Numbers of outputs m as well as structures of corresponding superposition and interference operators are presented in [7] for different QAs.

Fig. 2 shows the general structure of QA that includes almost of described peculiarities.

Quantum massive parallel computing

SCO

Quantum KB optimizer

I ^N } = [ ( Interference )( Quantum oracle ) ] ( Superposition ) ^^^

^Answer     QC output      QAG design

Coding of function properties

Fig. 2. General structure of QA

C lassical input Problem

The quantum circuit is a high-level description of how these smaller matrices are composed using tensor and dot products in order to generate the final quantum gate as shown in Fig. 1. QA structure has three main quantum operators: superposition; entanglement (quantum oracle) and interference in quantum massive parallel computing.

Information and thermodynamic trade-off between control quality measures

For Fig. 3 the following notations are introduced: V – Lyapunov function; S, S entropy production in the of control object (Plant) and the regulator (Controller), respectively; Let us V – Lyapunov function as v=12L»1+1S!; S=S-Sc

- generalized entropy of control system; q( = p( q,, S.u, t) - the equation of motion of the plant; q – generalized coordinate; u – the desired control.

Assume that the control object is described in General form by the equation q _; = ^ ( q, , S . u , t ) , where q is the generalized coordinate and describes the movement of the control object, u is the control and S ( t ) = S p ( t ) - S c ( t ) is the generalized entropy of the system, as the difference between the production of entropy control object S and the entropy production control S by the regulator. Let us V – Lyapunov function as V = 1 ₂ ”₄ q 2 + 1 S ²; S = S_p - S_c and consider the following equation:

dV=1 2 q^( q, t,S (t), u )+( Sp - Sc )(Sp - Sc ).

Equation (1) relates in analytical form such qualitative concepts of control theory as stability V (Lyapunov function), controllability and robustness based on the concept of entropy of phenomenological thermodynamics [1].

This approach allows, as noted earlier, to find the necessary distribution between the levels of stability, controllability and robustness, which allows to achieve the goal of control in Unforeseen situations with a minimum consumption of useful resource by using as a fitness function in the genetic algorithm the minimum production of generalized entropy, which is included in the right part (1).

For Fig. 3 the equation of distribution of qualities of control of dynamic system connects in the analytical form on the basis of concept of entropy of phenomenological thermodynamics such qualitative concepts of the theory of control as stability, controllability and robustness.

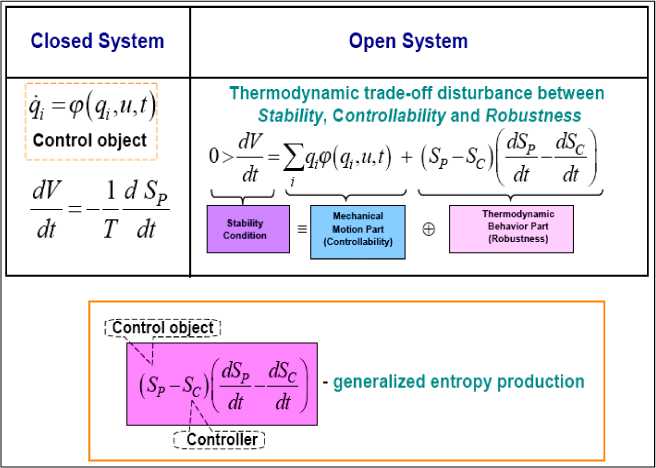
Fig. 3. Thermodynamic criterion of distribution of quality of robust control

As a result, the necessary distribution between the levels of stability, controllability and robustness, as a function of suitability in the genetic algorithm, the criteria for the minimum production of generalized entropy are used, which allows to achieve the goal of control in Unforeseen situations with a minimum consumption of useful resources.

The thermodynamic definition of S and information entropy H are related by the von Neumann relation

n as: S = kH = -Ep. In p., where k ® 1.38 -10—23 and is the Boltzmann constant. Consider now (1) with i=1

regard to the relation of thermodynamic entropy to Shannon information entropy. Substitute the Shannon information entropy - H in equation (1) instead of S ( t ). As a result, we obtain:

n

"T = T E q M q , t , k ( ^HC - H p ) , u ) + k ( ^HC - H p ) ( ^HC - H p ) ^ 0 .          (2)

dt 2 i = 1

Thus, Eq. (2) also relates stability, controllability and robustness, but already on the basis of Shannon information entropy, which also allows to determine the control for the guaranteed achievement of the control goal in unforeseen situations with the requirement of a minimum amount of information about the external environment and the state of the control object. Consequently, (1) and (2) constitute a system of equations, the solution of which determines the control, guaranteeing the achievement of the control goal in unforeseen situations with a minimum consumption of useful resources and the minimum required initial information [1, 4].

Quantum fuzzy inference based on quantum genetic algorithm in intelligent robotics

PID controller is a widespread type of controller in control loops. The controller is used in 70% of the industrial automation, most of them require constant adjustment, as a result of which they do not work very effectively, especially if the situation differs from the calculated one. Increasing robustness and efficiency is possible through the use of quantum computing and quantum search algorithms, and as a special case -quantum fuzzy inference (QFI). Without increasing the cost of a temporary resource – in online.

An example of such a control structure is shown in figure 4, which shows the integration of several fuzzy controllers into a single control system in the QFI block which allows creating a new quality in control – online self-organization of KB [1]. In general, the structure of a QAG based on a QGA described in (1) in the form:

QAG = [ ( Int ® ⁿ I ) • U_F ] h + 1 • [ QGA ] [ ⁿH ® m S ] .

QGA have already been actively used in human action recognition [5] and fault diagnosis of gearbox [6]. Structure of corresponding QAG on Fig. 4 is shown.

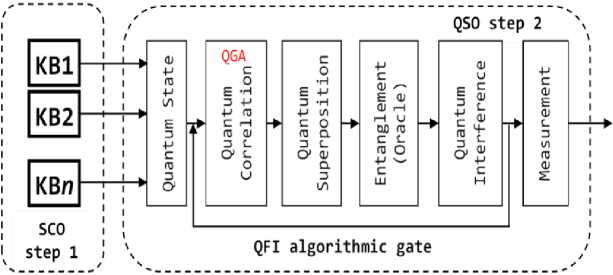
Fig. 4. QAG structure of QFI with QGA

The first part in designing Eq. (2) is the choice of the type of the entangled state of operator U . Developed by quantum genetic search algorithm (QGSA) (see, Fig. 5), is the basic unit of such an intelligent control system (ICS).

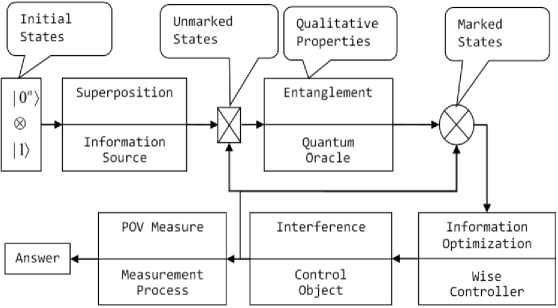
Fig. 5. Intelligent self-organizing quantum search algorithm for intelligent control systems

Results of simulation show computing effectiveness of robust stability and controllability of (QFI + QGA)-controller and new information synergetic effect: from two fuzzy controllers with imperfect knowledge bases can be created robust intelligent controller (extracted hidden quantum information from classical states is the source of value work for controller [1]) in on-line. Intelligent control systems with embedding intelligent QFI-controller can be realized either on classical or on quantum processors (as an example, on D-Wave processor type).

Two classes of quantum evolution (1) are described: QGA and hybrid genetic algorithm (HGA). The QFI algorithm for determining new PID coefficient gain schedule factors K (see, below Fig. 6) consists of such steps as normalization, the formation of a quantum bit, after which the optimal structure of a QAG is selected, the state with the maximum amplitude is selected, decoding is performed and the output is a new parameter K.

At the input, the QFI obtains coefficients from the fuzzy controller knowledge bases formed in advance based on the KB optimizer on soft computing. The next step is carried out normalization of the received signals [0, 1] by dividing the current values of control signals at their maximum values (max k), which are known in advance.

Formation of quantum bits. The probability density functions are determined. They are integrated and they make the probability distribution function. They allow defining the virtual state of the control signals for generating a superposition via Hadamard transform of the current state of the entered control signals.

The law of probability is used: p (| 0 ) ) + (|1 > ) = 1 , where p (| 0 ) ) is the probability of the current real state and p (| 1 ) ) is the probability of the current virtual state. The superposition of the quantum system "real state – virtual state" has the form (4)

I r ) = 1 (     '    ' 1 0) + ,/1 - P (i 0> ) 1 ) .                                     (4)

The next step is selection of the type of quantum correlation – constructing operation of entanglement. Three types of quantum correlation are considered: spatial, temporal and spatial temporal. Each of them contains valuable quantum information hidden in a KB .

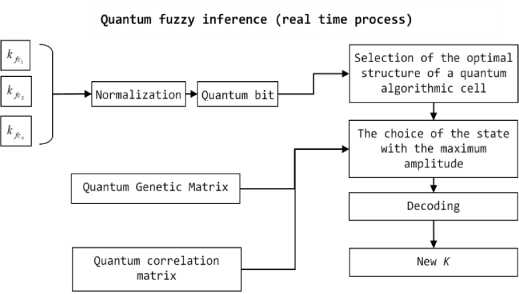
Fig. 6. Quantum fuzzy inference algorithm

Quantum correlation considered as a physical computational resource, which allows increasing the successful search for solutions of algorithmically unsolvable problems. In our case, the solution of the problem of ensuring global robustness of functioning of the control object under conditions of unexpected control situations by designing the optimal structure and laws of changing the PID -controller gain factors by classical control methods is an algorithmically unsolvable problem. The solution of this problem is possible based on quantum soft computing technologies [1, 4]. The output parameters of the PID -regulators are considered as active information-interacting agents, from which the resulting controlling force of the control object is formed. In a multi-agent system, there is a new synergistic effect arising from the exchange of information and knowledge between active agents (swarm synergetic information effect) [2]. There are several different types and operators of QGAs [3]. QGA and HGA are tested on example of the roots searching task of equation.

Remark. One of the interesting ideas was proposed in 2004, taking the first steps in implementing the genetic algorithm on a quantum computer [1, 2]. The author proposed this quantum evolutionary algorithm, which can be called the reduced quantum genetic algorithm ( RQGA ). The algorithm consists of the following steps: 1) Initialization of the superposition of all possible chromosomes; 2) Evaluation of the fitness function by the operator F; 3) Using Grover's algorithm; 4) Quantum oracle; 5) Using of the diffusion operator Grover G; 6) Make an evaluation of the decision. The search for solutions in RQGA is performed in one operation. In this case the matrix form is the result of RQGA action [7].

Benchmark Inverted pendulum

This is a typical Benchmark of control theory, they demonstrating a quality of control system. Task of

control is to achieve the stability of inverted pendulum in vertical position. The motion of the dynamic

system “cart – pole” is described by the following equations (control object is an essentially nonlinear

dissipative system):

g sin e + cos e

u + ^(t) + axz + a3z - mle sin 6

e =

m_c + m

^r 4 m cos² 6

—

v 3   mc + m v

- k6

u + £ ( t) - axz - a^z + ml (02 sin 6 - 6 cos 6) z =          mrm

A mathematical model (4) of the control object presented above contains the following variables: 6 is the pendulum deviation angle (degrees); z is the movement of the cart (m); g is the acceleration of gravity (9.8 m/s2); mc is the pendulum mass (kg); l is the pendulum half-length (m); ^(t) is the stochastic excitation; and u is the control force acting on the cart (N).

Note that the model has underdetermined parameters such as friction in the pendulum shaft and friction surface on the wheel. Verification of the model with these parameters was considered in [8 – 10].

Compare the different regulators: classic PID -controller, with constant coefficients, fuzzy controllers FC 1 and FC 2, based on SCO , and QFI controllers based on different types of correlations: Quantum-SpaceTime ( Q-ST ), Quantum-Time ( Q-T ), Quantum-Space ( Q-S ). These QFI controllers are based on FC 1 and FC 2, and optimized using remote connection.

The mathematical modeling and physical experiments in two situations control:

• -    typical situation (S1), the delay of control is standard – 0.015 sec;

• -    unforeseen situation (S2), the delay of the control error – 0.035 seconds.

The simulation results are shown in Fig. 7.

Mathematical modeling and experimental results are received for the case of unpredicted control situation and knowledge base of fuzzy controller was designing with SW of QCOptKBTM for teaching signal measured directly from control.

As model of unpredicted control was the situation of feedback sensor signal delay on three times. Results of controller’s behavior comparison confirm the existence of synergetic self-organization effect in the design process of robust KB on the base of imperfect (non-robust) KB of fuzzy controllers.

In unpredicted control situation control error is dramatically changing and KB responses of fuzzy controllers ( FC 1 and FC 2) that designed in learning situations with soft computing are imperfect and do not can achieve the control goal. Using responses of imperfect KB (as control signals for design the schedule of time dependent coefficient gain in PID -controller) in Box QFI the robust control is formed in online.

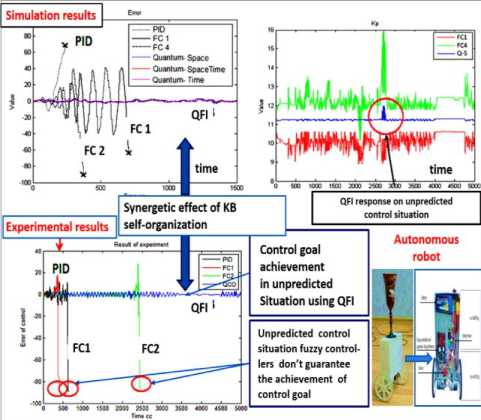
This effect is based on the existence of additional information resource that extracted by QFI as quantum information hidden in classical states of control signal (as response output of imperfect KB’s on new control error) [7 – 10].

Robotic Manipulator: Quantum supremacy

The seven degrees of freedom (7 DoF ) and seven-link robotic manipulator is described in this part.

Due control object is complex, ICS for 7 DoF manipulator is constructed with using decomposition principal. Seven independent FCs ( FC 1 – FC 7) are used for control each of manipulator link. The decomposition of control allows reducing complexity of constructing ICS .

However, character of ICS somewhat reduced due to independence of seven FCs (Fig. 8).

QFI unit introduction allows improving ICS behavior by self-organization of independent KBs in FC 1 – FC 7.

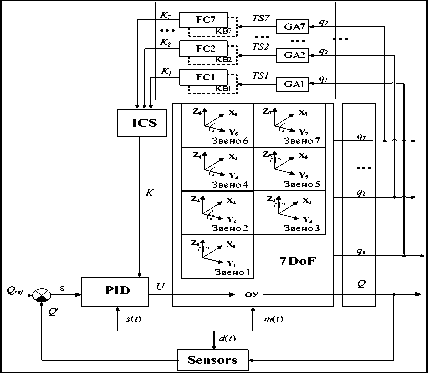
Fig. 8. The structure of 7DoF manipulator ICS

Consider the first internal unpredicted situation – the random noise in the control channel (see, the signal s ( t ) on Fig. 8). Comparison of manipulator behavior for control system based on soft computing and based on quantum soft computing in performance criteria terms is shown in Fig. 9 (on the base results of sixty-five experiments).

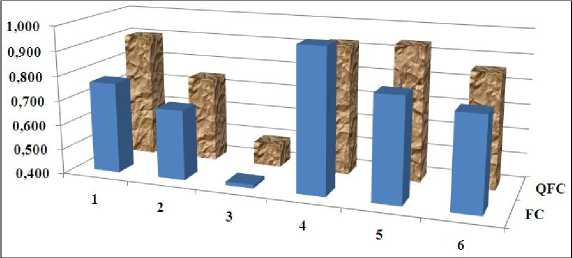
Fig. 9. Manipulator behavior with random noise in the control channel: FC – based on soft computing, QFC – based on quantum soft computing

The results are demonstrating if ICS is used with QFI gate, all of evaluation of performance criteria improve (expect “One iteration time”).

The one of cases is shown in Fig.10 (a). Positioning accuracy is better if used ICS with QFI unit (in this case positioning error is 0.184 m). Positioning error is 1.918 m, if used ICS without QFI unit.

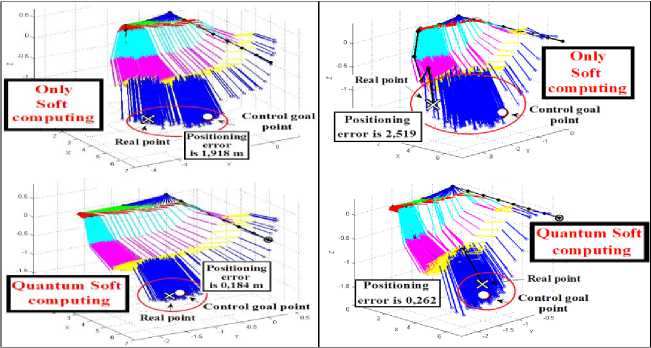
Fig. 10. (a) Manipulator behavior with random noise in the control channel, (b) Manipulator behavior with random noise in the measurement system

Consider the second internal unpredicted situation – random noise in the measurement system (see, the signal d ( t ) and “Sensors”, Fig. 8). Comparison of Manipulator behavior for control system based on soft computing and based on quantum soft computing in performance criteria terms is shown in Fig. 11.

The results are demonstrating if ICS is used with QFI unit, all of evaluation of performance criteria improve (expect “One iteration time”).

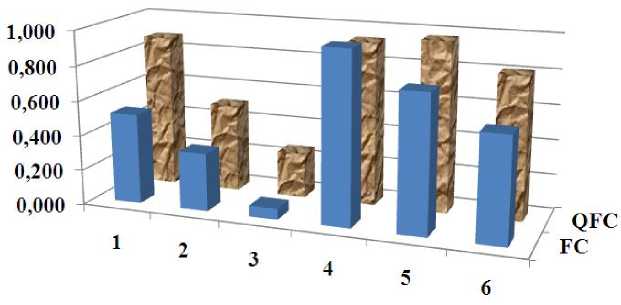
Fig. 11. Manipulator behavior with random noise in the measurement system

The one of cases is shown in Fig. 10 ( b ). Positioning accuracy is better if used ICS with QFI unit (in this case positioning error is 0.262 m). Positioning error is 2.519 m, if used ICS without QFI unit.

Conclusions

Physically, the synergistic effect means self-organization of knowledge and the creation of additional information, which allows the multi-agent system to perform the most useful work with minimal loss of useful resource and with a minimum of necessary initial information, while not destroying the lower, executive level of the control system. Together with the informational-thermodynamic law of intelligent control (optimal distribution of control qualities as "stability – controllability – robustness"), the IMS , developed as a multi-agent system, effectively ensures the achievement of the control goal under conditions of uncertainty of initial information and a limited useful resource.

Currently, end-to-end quantum information technologies have become widespread in such areas as unstructured database search, artificial intelligence, intellectualization of production processes, intelligent cognitive robotics, and many others. The development of this direction has made it possible to test a number of new types of algorithms for analyzing and processing data, which have proven themselves in the tasks of teaching and robust control of complex and weakly formalized objects, which sometimes function in emergency and unforeseen situations. These algorithms include, in particular, quantum algorithms for searching and retrieving knowledge, quantum neural networks and quantum genetic algorithms (see, Fig. 12).

New circuit implementation design method of quantum gates for fast classical efficient simulation of search QAs is developed. Benchmarks of design application as Grover’s QSA and QFI based on QGA demonstrated.

Applications of QAG approach in intelligent control systems with quantum self-organization of imperfect knowledge bases are described on concrete examples. Quantum supremacy demonstrated.

Results of controller’s behavior comparison confirm the existence of synergetic self-organization effect in the design process of robust KB on the base of imperfect (non-robust) KB of fuzzy controllers: from two imperfect KB with quantum approach robust KB can be created using only quantum correlation. In classical intelligent control based on soft computing toolkit this effect is impossible to achieve.

Quantum End-to-End Information

FackgrounIof Quantum Computational Intelligence

Quantum Soft Computing

Technology of Computational

Models of Applied Intelligent Toolkit

Quantum Deep MachineLearning with Applications

Physical Models Design from Experimental Data

Quantum Intelligent Contro^

Q Experiment Design uantum Search

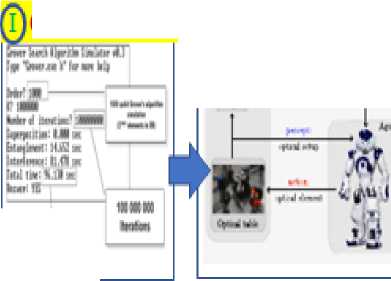
hh*te 1«M

Applications

^NICAmega-aiente project, JINR, Dubna

Intelligence:

• *    Al ecosystems;

• *    Physical equipment;

• *    Intelligent control;

• *    Cognitive systems;

• *    Intelligent robotics;

• *    Cognitive robotics;

• *    Quantum communication;

• *    Computational Intelligence Toolkit;

• *    Quantum algorithms of Analytic Big Data

• *    Quantum relativistic informatics

Fig. 12. Background of quantum computational intelligence

The research results were presented at the All-Russian Scientific and Practical Conference «NATURE. SOCIETY. MAN», Dubna University, 2020.