Quantum wavelet transforms generated by the product of the sine polynomial and the gaussian envelope on the tetrahedral graph

Published Online July 2018 in MECS DOI: 10.5815/ijigsp.2018.07.02

Graphs are mathematical objects that allow representing complex structures and facilitate their study [1]. In the last decade graph signal processing has been a hot subject in signal and information processing for different reasons [2]. Graphs are modeling tool suitable to many applications such as social and economic networks, epidemiology and biological networks, transportation networks, information networks, internet blog data, power grids arising in large variety of applications, generate large sets of raw data from which a detailed analysis may extract useful information [3]. Some data on this graphs can be modeled as scalar (or vectors) functions on each of its nodes, forming what is called signal graph [4]. A first step in modelling a graph signal consists of the construction of the appropriate signal transforms [5]; this would require the modeling of signals on graphs characterized by a connectivity or adjacency matrix that captures dependencies in the data [7], [6]. The eigenvalues of the Laplacian matrix give the discrete spectral frequencies [6]. In [7] Sandryhaila and Moura defined a shift or translation of the graph using adjacency matrix and arrived at notions of graph linear filtering and graph Fourier transform (GFT). In this context then the graph Fourier transform is defined as a projection on the generalized eigenvectors of the Laplacian matrix. This operator point of view allows not only to generalize the notion of transforms but also the notions of filtering and other general linear operations on graph signals [5]. There is an extensive literature that explored algebraic graph theory, spectral graph theory and wavelets transform on graphs [8], [9], [10] and [11] and references therein.

Graphs formally represent a network, which is basically a collection of interconnected objects. A network picture has been applied to various physical and biological systems to understand their governing mechanisms intuitively. Utilizing discretization schemes, both electrical and optical materials can also be interpreted as abstract ‘graph’ networks composed of couplings (edges) between local elements (vertices), which define the correlation between material structures and wave flows [12]. Chensheng Wu et al. [13] used a plenoptic wave front sensor to image the distorted beam into its 4D phase space. A fast reconstruction algorithm based on graph theory was applied to recognize the phase distortion of a laser beam and command the adaptive optics (AO) device to perform phase compensation. In [14] authors provided an experimental demonstration of how a fiber network can be treated as an optical oracle for the Hamiltonian path problem, the famous mathematical complexity problem of finding whether a set of towns can be travelled via a path in which each town is visited only once. In order to solve this Hamiltonian path problem, the graph was implemented as a network consisting of optical fibers (roads) that connected all of the five nodes (towns), and the network was probed using a short optical pulse.

Quantum computing is at the interface of quantum physics, mathematics and computer science. Quantum information theory has been investigated in connection with quantum algorithms and communication protocols using density matrices and operators associated with tensor-product of Hilbert vector spaces. In [15] authors showed a strong link between quantum experiments and graph theory. In the experimental setups to realize high dimensional multipartite quantum states each of the setup corresponded to an undirected graph, and every undirected graph corresponded to an experimental set up. A link between quantum physics and graph theory has been drawn before, but for different reasons [16]. For example, in Graph states [17], [18], which are related to the resources for measurement-based quantum computation [19], the vertices of the Graph correspond to qubits in a quantum state, and the edges correspond to correlations between two qubits. In different works, the Laplacian of a graph has been interpreted as the density matrix of a quantum state [20] with the Hamiltonian of such system approximated by the adjacency matrix of the graph, and the energy levels and states represented by eigenvalues and eigenvectors [21], this allowed to investigate new entanglement criteria [22].

The objective of this paper is to investigate the product of the sine polynomial and the Gaussian envelope which yields the matrix of vertices of the tetrahedral graph. The spectral analysis shows interesting properties of the Laplacian matrix, adjacency matrix and the eigenvalues matrix of the tetrahedral graph with applications in matrix representation of quantum gates. This paper is organized as follows: section II overviews the background and concepts from quantum graph, quantum logic gates and quantum wavelet transforms. Section III discusses the like Schrödinger Equation for the wavelet function consisting of a sine polynomial of four sinusoidal waves into a matrix of vertices of the tetrahedral graph. Section IV discusses the results out of this paper that include the modelling of quantum logic gates using the matrices derived from the tetrahedral graph. Finally, section V winds up with the conclusion highlighting an open up for future research directions that will arise out of this work linking the graph theory, the wave propagation theory, quantum theory and molecular orbital structures. This paper will obviously serve as a foundation for a variety of useful applications of graph theory to quantum image processing and quantum data compression and related areas.

• II.    R elated W orks

Quantum computation and quantum information are modern developments taking advantage from the Quantum Mechanics features to propose technological applications. Quantum mechanics deals with microscopic objects like atoms, molecules, etc. Here the consideration is given to only those quantities which may be measured. The evolution of quantum systems is completely determined by its Hamiltonian. The latter describing the quantum system exponentiated to produce a unitary operator. In the case of time-evolution, it is possible to achieve the same unitary transformation with different Hamiltonians, since the former is only concerned with the input and output of the transformation and not the intermediate state of the system. This is one reason for why there are so many different proposals for performing quantum computation in different physical settings [23].

The evolution of quantum systems is completely determined by its Hamiltonian. Pauling introduced quantum graphs of connected one-dimensional wires some decades ago [24]. Later Kuhn used Pauling’s idea [25] to describe organic molecules by free electron models. Some of the physical systems modeled by quantum graphs include electromagnetic waveguides [26], [27], mesoscopic systems [28], quantum wires [29], [30], excitation of fractons in fractal strictures [31], [32].

Quantum graphs with external leads (antennas) have been analyzed in detail in [33],  [34]. In [35] authors investigated Wigner’s reaction matrix using tetrahedral microwave networks that correspond to graph with the time reversal symmetry в = 1 . In [36] the author attempted to model electrical network using graph theory. The most fundamental concept of classical computation and classical information is Bit (binary digit). This is a system that can take on one of two values, such as true and false or 0 and 1. Qubit (Quantum bit) is the quantum analog of a bit. Classical computer circuits consist of wires and logic gates. In a similar way, quantum computer has a quantum gates from which quantum computing devices are designed. Quantum gates on a n-qubit can be described by a 2n by 2n matrices. Because of the normalization condition that requires

z ,  k, 1=i             (1)

there constrain for matrices which can be used as quantum gates. The matrix U describing the quantum gate should be unitary that is, U ^U = I, where I is the identity matrix [37]. The action of quantum logic gates is always logically reversible [38]. Construction of quantum gates from the elementary braid matrices of the stocks prices closely follows the work of L. S. Geogiev [45], [46], [47]. Hadamard gate, Pauli gates or Controlled-Z gate are some of the elementary quantum gates that are identified in the stock market structure [48]. The Fourier and Walsh-Hadamard transforms have been the ones studied most extensively by the quantum computing community [39],  [40],  [41]. The quantum Fourier transform (QFT) is now recognized as being pivotal in many known quantum algorithms [42]. Amir and Colin derived efficient, complete, quantum circuits for two representative quantum wavelet transforms, the quantum Haar and quantum Daubechies D(4) transforms. Their approach was to factor the classical operators for these transforms into direct sums, direct products and dot products of unitary matrices. They found that permutation matrices play a pivotal role in the development of wavelets transform and arise explicitly in the packet and pyramid but also in the factorization of wavelet kernels. they considered the particular set of permutation matrices arising in quantum wavelet transforms and developed efficient quantum circuits that implement them. Wavelet transforms are useful for quantum image processing and quantum data compression. It is natural therefore to consider how to achieve a quantum wavelet transform [39], [43]. The author in [44] calculated the admissibility constant and the demonstrated the covariant of Morlet wavelets, and hence eliminated two of the barriers to full use of this powerful technology for the analysis of foundational questions in quantum mechanics. He took the four-dimensional mother Morlet wavelet as the direct product of four one-dimensional mother Morlet wavelets, one for each coordinate.

to = 2 а ² п + п + 1 с у₂ = 2 ст²п — п + 1 ^ = 2 а ² п + п — 1 су₄ = 2 ст²п — п — 1

Given the Schrödinger wave equation:

III. S chrodinger L ike E quation F or W avelets

Computation of high frequency waves is a necessity in many scientific applications [72]. Fields requiring such computations include the semi-classical limit of the Schrödinger equation, communication networks, radio antenna engineering, laser optics, under water acoustics, seismic wave propagation, and reflection seismology [32]. Christopher L. Mueller [49] and H. Kogelinik and T. Li [50], used the concept of electromagnetic wave beams to describe mathematical techniques for Resonant Interferometer and Laser beams resonators. Gaussian beams are approximate high frequency solutions to PDEs which are concentrated on a single ray through spacetime. The quantum amplitude T linked to a quantum object satisfies the differential wave equation:

V ² ^ = 1^             (2)

d t ²

where V is the Laplacian operator and T represents a space filling and time-dependent physical field [51]. It is known that in most cases the laser beam is similar to plane waves; except that their intensity distribution is not uniform [50]. In this paper we will attempt to use the optical differential wave equation and the sine polynomial windowed by a Gaussian envelope to model some optical, microwave and radar system elements and some quantum phenomena based on the matrix of vertices of the tetrahedral graph to easy the computation complexity of PDEs.

In this paper, we consider the modulated wave form given by Eqn. (3) whose plane representation is shown in Fig.1.

T ( t ) = 100 cos(2 a ² п t ) sin( п t ) cos( t ) e ^а      (3)

Applying Euler’s formulae on Eqn. (3) and simplifying expressions transforms it into a family of sine polynomials given in Eqn. (4).

d ²

--- sin kt = —k sin kt      (6) 2 m dt ²        2 m

Й is the Plank’s constant divided by 2 п and — is the mass of the particle that is traveling through space, sin kt is an eigenfunction of the Schrödinger equation, the eigenvalue k ² is the energy. The compact form of the Schrödinger equation is:

where

H T = E T            (7)

2 _d 2

I =---у               (8)

2 m dt

is the energy operator,

E =——k¹

2 m

is the energy eigenvalue or energy whereas T = sin kt is the wave function. The complete solution with boundary conditions is the linear combination of partial solutions; then we have:

T ( t ) =

[2 ^ . пя V L ^^s,n E

Note that n is a quantum number [70]. The mathematical model describing the higher order light beams is a product of Hermite function and Gaussian functions [50].

T —n ( r , t ) =

V ^ 2 ⁿn ! 4л

H mn

From Eqn. (4) we define the phase-space transformation matrix given by:

where

T - (t )=

²⁵ Z sink to - 1 )

— = 1

—

e ² " ²

	^ 2.па 2	2 п^ 2	2-па 2	2 па 2
P =	п	—п	п	— п	(12)
	I 1	1	— 1	— 1 J

After performing some operations on the transformation P then we get the matrix representing the vertices of the tetrahedral graph given by:

Multilevel block partitioning is of interest only if the blocks of the levels exhibit some structure [55]. U , V and W exhibits block structures. U and W have the following block structures:

'+1  +1  +1+Р

R = +1  -1  +1

V+1  +1  -1

( C C )      _

^U = ^ ^c cj; W = ^

— C ) + C V

The column vectors are the vertices of a family of tetrahedrons defined in a 3-dimension real space R ³ . The coordinates of the tetrahedron at the origin and those of the dual tetrahedral graph refer to [52]. Therefore the tetrahedron set of vertices V has the cardinality of 4 ( # V = 4 ) i.e. four vertices and the set of edges E has the cardinality ( # E = 6 ) i.e. six edges. Note that the tetrahedron, the octahedron, and the cube are the only “Platonic” solids that exist in any dimension [53]. For the properties of tetrahedral graph refer to [54]. Each vertex of the tetrahedral graph corresponds the quantum number.

where C is the Temperley-Leib generator given by:

1/ d 1/ d         1  1

= —

V 1/ d 1/ d J   V2 V 1  1 J

For the Ising anyons model, the Kauffman variable n is Z = i e 8 , and the quantum dimension of the spin

1/2 is d = V2

Alternatively, matrices U, V and W can be expressed as follows:

• IV. R esults A nalysis

• A. Spectral Analysis

In this section, we are interested in computing the product of the Matrix P and its transpose as follow:

F = P T x P            (14a)

we get the following matrices:

F = 4 n ² a ⁴ ( uu T ) + n ² ( vv T ) + ( ww T ) (14b)

W = D — A + N — M(17a)

V = D — A+M — N(17b)

V + W = 2 D—2 A = 2 L(17c)

Where

L =

(+ 1

^^^^^e

+ 1

—

—

+ 1

;

D =

■

V

—

+1J

V 0

V

( 0

F = 4n2 a 4U + n 2V + W       (14c)

A =

;

M =

The product of the transformation matrix R and its transpose PT x P indicates that the transformation representing the wavelet transform on a bipartite regular undirected graph. We realize that the product F is a linear combination of three Gram matrices U , V and W , where U = uu^T , V = vv^T and W = ww T

V

0 J

u =

V =

N =

( 0

0 )

;

Q =

V

V

Vv

(+ 1

—

+ 1

' V

—

—

+ 1 )

1   1   1 )

; v =

— 1

+ 1

—

+ 1

+ 1

' V

—

1 J

+ 1

—

+ 1

—

; w =

^^^^^e

+ 1

—

+ 1J

+ 1

—

;

U =

V

—

V

1   1   1 ^J

, W =

(+ 1

+ 1

—

' V

—

+ 1

+ 1

—

—

— 1   — 1 )

— 1

+ 1

— 1

+ 1

+ 1   + 1 ^J

V 0

0 J

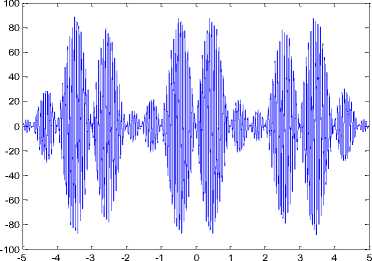
Fig.1. Plot of the wavelet transform in Eqn.(3) for 2 a ² = 230

with L = D - A being the Laplacian matrix, A , the adjacency matrix, D the degree matrix and Q = D + A , the signless matrix of the tetrahedral graph. The eigenvectors corresponding to different eigenvalues are orthogonal and therefore the adjacency A matrix is orthogonally diagnosable. The diagonisation means that there exists a diagonal matrix Л such that:

P l ( д ) = P q ( д ) = ( p I - A ) = X( P - 2) 2     (22a)

The eigenvalues of the Laplacian matrix

P 1 = P 2 = 2; P 3 = P ₄ = 0          (22b)

and we realize that the square of the matrix V_L

where

A = V_AЛ_А V_A ^{- 1} = V_AЛ_А V/     (19)

A AA   A AA

diagonalizing the Laplacian matrix is described by:

V a — 1 = Va^T

U, V, W, D, L e Spect4 = { X e S4+1 Tr(X) = 4} where S4+ is the set of 4 x 4 positive semi-define matrices and Tr(X) is the trace of the matrix X . This means that the matrices U,V,W, D, L and Q having the same trace equal to one and belong to the same spectrahedron of the tetrahedron which is the subject of investigation. The matrices U, V and W, are circulant matrices and we know that circulants are a special type of Toeplitz matrix and have unique properties. Looking at the tetrahedral graph we see that its adjacency matrix is symmetric and we can find its eigenvalues. They are obtained by solving the characteristic polynomial to zero.

P_a ( X ) = ( X I - A ) = ( X - 1)²( X + 1) 2       (20a)

The roots which are eigenvalues having the following values:

X 1 = X 2 = — 1 , X = X = 1         (20b)

The eigenvalues matrix associated with the adjacency matrix A of the tetrahedral graph is:

	' 100 0 л
22	0010	(22c)
LQ	0 10 0
	, 0  0  0   - 1 v

We have the following matrix equations from the tetrahedral graph:

A ² = M ² = N ² = D = I

A x M = M x A = N

A x N = N x A = M

M x N = N x M = A           ₍₂₃₎

Q + M + N = D + A + M + N = U

R T x R = 3 D - A + M + N

M + N = R T x R - 3 D + A

( M + N )² = 2 D + 2 A

^A = ^A K ₄,₄ ^{+ A} C ₄    ^A K ₄            ⁽²⁴⁾

	r- 1	0	0	0
	0	- 1	0	0
л^=
A	0	0	1	0
	. 0	0	0	1

(21a)

The square of the matrix V_A   diagonalizing the

adjacency matrix is described by:

0   0  1 )

A

0   - 1

0 J

(21b)

where A_K , A_C and A_K are the adjacency matrices of the complete bipartite graph, the cyclic graph and the complete graph respectively.

(xi)The degree matrix D is also a product of a Haar transform matrix of order 4 and its transpose, that is,

D = H T H 4                 (25)

B. Generalize Gell-Mann Matrix Basis

In this paper, we will discuss three different bases that can be used to decompose the matrices derived from the t tetrahedral graph. We begin with the generalized Gell-Mann matrices which are higher–dimensional extensions of the Pauli matrices (for qubits) and the Gell-Mann matrices (for qutrits), they are the standard SU ( N ) generators[84]. The six symmetric Gell-Mann matrices of SU (4) are given below:

The vectors of V form an orthonormal basis of R ⁴ .

The Laplacian characteristic polynomial

	' 0 0 10 ^		' 0  0  0  0 '
\ '   =	0  0  0  0	Л 24 =	0  0  0  1
s	1000	s	0  0  0  0
	ч 0  0  0  0 7		( 0  1  0  0 J

		r 0	0	0	1	)		r 0	0	0	0
		0	0	0	0			0	0	1	0
Л 14 =							л 23 =					(25a)
s		0	0	0	0		s	0	1	0	0
		к 1	0	0	0	)		к 0	0	0	0
	r	0	1	0	0 )			0	0	0	0 )
Л =		1	0	0	0		л 334 =	0	0	0	0
s		0	0	0	0		-	0	0	0	1
	к	0	0	0	0 )			0	0	1	0 )

C. Frames and Hadamard-Walsh Transform

In this section we consider the frame

F₂ = V 1 , V 2 , V 3 , V 4 defined by the following vectors:

Let us express the adjacency matrix A of the tetrahedral graph as a function of the generalized Gell-Mann matrices:

V 1 =

'+ Г

+ 1

+ 1

1+1)

—

, V 2 =

к

—

Г+ 1 )

+ 1

	r+ 1 + 1		r+ [ ) — 1
V 3 =	— 1	and V 4 =	— 1
	k— 1 )		k+ 1 )

A = Л-4 + Л23

From Eqn. (23a) and (25a) then the degree matrix D is given by:

12 2        13  2        14 2        23

D = (Л- ) = (Л- ) = (Л- ) + (Л- )

with

Л-4 Л 23 = Л23Л-4 = 0

Since the two matrices are linearly independent. We can see that at the center of the matrix Л 2³ there is the submatrix of adjacency matrix Hamming cube of order one. The consequence of the above statement is that the Laplacian matrix L is given by:

L = D — A = (л23 )2 + (Л-* )2 — (Л23 +Л24)

and therefore, the signless matrix Q is equal to:

Q = D + a = ( л 2³ ) ² + ( Л - ⁴ ) ² + Л 2³ + Л - ⁴ (25f)

(A2 + A2)2 = (A2 + A )2 = Ai2 + A2

M = Л13 + Л24

N /V +Л34

2             2              22

Л24 ) +(Л-3) =(Л-4 ) +(Л23 )

Л 24Л-3 = 0

is a group under component wise multiplication. Any group of order p or p ² , p a prime is necessarily abelian [57]. The matrix W corresponds to the character table of the point group C symmetry where following equations:

E = V = uC2 = V = v i = V = w

^ h = ^V 4

V = V2 x V X V4

V 2 = V 3 x V 4

V 3 = V 2 x V 4

V 4 = V 2 x V 3

Let us consider the matrix W made of the column F ₂

vectors of the frame F ,

WF = F2 Г1 1 1 к1 1 —1 1 —1 1 1 — 1 — 1 1 ^ — 1 — 1 1 ) (29a) WF2 = WTP4 (29b) where r 1      1 1 1) r 0 0  0  1) —1  — 1 1 1 0 0  1  0 WT = and K = —1    1 1 —1 1 000 к1   —1 1 -1 1) к0 1  0  0) are the Walsh transform matrix for a 4x4 image and the permutation of coordinate axes respectively. It is easy to show that:

P ^ = [ H ( " ) ml,.v      (32a)

K2 = N, K3 = M, K4 = D, K5 = A   (29c)   with

H ( m ) =--- £ e "^ H¹, ( m A )     ^(33b)

|det( A) 2 , ^er

Using Eqn. (29c) then Eqns. (17a), (17b) and (17c) become:

V = K 3 + K 4 - K 2 - K 5				(29d)	where A e Zd x d is an expanding dilation matrix. Each polyphaser matrix contains the degree matrix D of the tetrahedral graph and it is expressed in term of matrices
W = K	+ K	- K"	- K	(29e)	in Eqn. (33 f ) as follows:

V + W = 2K4 - 2K5 = 2L      (29f)

From Eqn. (23 d ) and (29c) one can obtain

A = MK2            (29g)

From the result in [71] and Eqn. (25c) we realize that the integration of the cross-product of two Walsh function vectors is the degree matrix of the tetrahedral graph:

D = B_o + B + B + B o + B 1 + B 4      (33c)

The matrix of eigenvalues of the adjacency matrix is given by:

A,   4 B ² - 4 B ²           (33d)

The permutation matrix N is the sum of two matrices 2 B ₂ and 2 B ₂ i.e.

J W(t) WT (t) = (Л4) +(л3 )        (30)

Where [59]

N = 2 B + 2 B        (33e)

The matrix W defined by the frame F contains four Dirac matrices. Reference to Table IV [58] given by M. Karlsson. we can express the matrix W_B in terms of four matrices as follows:

Wf, = i i Djk(31a)

k = 1 j = 1

Equivalently we have:

W = D— + D12 + D21 + D22

W3 = 4 Dn

Therefore, the square of the sum of the Dirac matrices D ₁₂ and D ₂₁ becomes

( D 12 + D 21 ) ² = r W f₂

— WF' - A = 2D + 2D„

4  F233

Now we consider the tight frame characterization of the multiwavelet vector [59] in terms of the polyphaser matrices:

		r 1100 "				r 1    - 1  0	0 "
1		0000		~	1	0  0  0	0
B n =-				, B 0 =
2		0000		2		0  0  0	0
		( 0000 y				( 0  0  0	0 .
		r 0  0  0  0				r 0  0  0	0 )
1		0  0  0  0		~	1	000	0
B =-				, B 1 =-
2		0011		2		001	-1
		( 0  0  0  0				ч 0  0  0	0 J
	r	0  0  0  0 л			r 0 10 0 л
1	0000			1	1000
B7 =-			, B =-				(33 f )
2   2	0001			2	0000
		0010 v			4 0  0  0  0 ,
		0  0  0  0 )				000	0	^
1		1100		~        1		- 11  0	0
B 4 = - 4				, B 4 = -	-
		0000		2		000	0
		0 0 11 ?				0   0   - 1	1	J

Therefore, the square of the matrix diagonalizing the

Laplacian matrix V L = V Q can be written as:

~~

V2 = B + B + A2 A + B + B - 4 B2    (34a)

Using Eqn. (25c) and (33c) one can obtain

22     ^~~~

D = ( л 1⁴ ) + ( Л 2 ²³ ) = B _o + B, + B ₄ + B о + B i + B 4

(34b)

Using Eqn.(25i) and (33e) one can obtain

N = Л12 + Л34 = 2 B2 + 2 B3       (34c)

Using Eqn. (23 d ), (25 b ) and (34 c ) above, one can obtain

M = AN 1 = Л3 + Л24 = (л14 + Л223 )(2B2 + 2B3Г (34 d)

Such that

(Л3 3 )2 = B0 + B0 + Bi + Bi(34e)

~

(Л 24) = B4 + B 4

₂ ~~

(Л34) = Bо + B0 - Bi - Bi + 4B22(34g)

(Л223) = 2 B + 2 B1 + B4 + B 4 - 4 B2'

The matrix W_B of the column vectors of the frame F ₂ is the Hadamard matrix H ₄ of the order 4. The quaternion units D = D ₀₀, iD_i3 , iD ₃₀ and D ₀₁ A link Williamson type and related Hadamard matrices [81].The Hadamard matrix H ₄ can be expressed in terms of the Hadamard matrix second order H as follows:

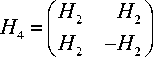
(35a)

The characteristic equation of the Hadamard matrix H ₄

P/ Я ) = ( X I - A ) = ( X - 2)²( Я + 2)²    (35b)

and

Л h4 = 2Л A

(35c)

where Л A is the eigenvalue matrix as defined in Eqn.(21a)

The matrix W of the frame contains the matrix R of F ₂

the vertices of the tetrahedral graph . In the Hadamard matrix of order 4 the first three columns constitute the matrix R defined by the vertices of the tetrahedron.

Hadamard transform finds practical application in many areas such as data encryption, signal processing, quantum information processing and data compression algorithms. The Fast Walsh Hadamard transform (FWHT) is used to obtain local structure of images. FWHT can be considered as a sparse factorization of the transform matrix, and refer to each factor as a stage. The property that relates matrix H with its inverse is given by:

HR" = R ” ( hr ” )^{- i}             (35 d )

where HR" = Radix-R Walsh Hadamard transform; R ” = radix-R factorizations ” = input element.The special aspects of WHT are the saving of time (48% compared with DF) [60]. Sasikala and Neelaveni [61] approached the problem of multimodality medical image with a fundamental concept of correlation coefficient as a matching measure and showed that the FWHT is faster than the Walsh transform (WT) reducing time consumption for medical image registration.

D. Qubits Solution to Yang-Baxter

Yang-Baxter equation has been studied as the master equation in integrable models in statistical mechanics and quantum field theory [54]. Many scientists have found solutions for the Yang-Baxter equation; however, the full classification of its solutions remains an open problem [55]. The problem of finding solutions to the Yang-Baxter equation that are unitary turns out to be surprisingly difficult [56]. Dye H. [57] described all unitary solutions to the Yang–Baxter equation in dimension four.

In this section, we consider the following Yang-Baxter equation:

( R ® I )( I ® R )( R ® I ) = ( I ® R )( R ® I )( I ® R ) (36 a )

where the matrix R is the unitary solution of the Yang-Baxter equation and I denotes the identity operator of order two. The matrix solution R is the universal quantum gate known as the familiar change-of-basis matrix from the standard basis to the Bell basis of entangled states. The above unitary braid matrix can be expressed in terms of the degree matrix and adjacency matrix of the tetrahedral graph as follows.

R = -^ (D + D01A)

where D and A are the degree matrix and the adjacency matrix of the tetrahedral graph respectively. We have the following identities:

(D01A) A = -A ( D01A)

-(VV) A = - A (-VA2VL2)(57b)

(D0i A )(-VA2VL2) = (-Va2Vl2)(D0i A)

,  ,        . Г 0   1 4 Г 01

- VAV2 = DWA =       ®

AL   01  (-10 J(