Quantumchemical calculation of some diols by method MNDO
Автор: Babkin Vladimir Aleksandrovich, Ignatov Alexey Viktorovich, Zakharov Dmitry Sergeyevich, Zaikov Gennady Efremovich, Fomichev Valery Tarasovich, Belousov Andrey Sergeyevich, Gulyukin Mikhail Nikolaevich, Ignatov Alexander Nikolaevich, Titova Evgenia Stanislavovna
Журнал: НБИ технологии @nbi-technologies
Рубрика: Социально-экономические инновации
Статья в выпуске: 2 (9), 2013 года.
Бесплатный доступ
Quantum chemical calculation of the molecules of 3,5-di(cyclo-trialumoxandiol)tetraalumoxantetraol-1,1,7,7and 1,7-di(cyclotrialumoxandiol)tetraalumoxantetraol- 1,3,5,7 is executed for the first time by method MNDO with optimization of geometry on all parameters by standardgradient method. The optimized geometrical and electronic structure of these compounds is received. Acid force of 3,5-di(cyclo-trialumoxandiol) tetraalumoxantetraol-1,1,7,7and 1,7-di(cyclotrialumoxandiol)tetraalumoxantetraol-1,3,5,7 is theoretically appreciated. It is established, that it to relate to a class of very weak H-acids (pKa=14) where pKa-universal index of acidity).
Quantum chemical calculation, метод mndo, method mndo, 5-di(cyclotrialumoxandiol)tetraalumoxantetraol-1, 7-di(cyclotrialumoxandiol)tetraalumoxantetraol-1, acid force
Короткий адрес: https://sciup.org/14968295
IDR: 14968295 | УДК: 547.854.83:544.183.25
Текст научной статьи Quantumchemical calculation of some diols by method MNDO
The Aim of this work is a quantum chemical calculation and theoretically determination of acid force of derivativesdioles3,5-di(cyclotrialumoxandiol) tetraalumoxantetra-ol-1,1,7,7and 1,7-di(cyclo trialumoxan-diol)tetraalumoxantetraol-1,3,5,7 by method MNDO with optimization of geometry on all parameters by standard gradient methodbuilt-in in PC GAMESS [10]. The calculation was executed in approach the insulated molecule in gas phase. Program MacMolPlt was used for visual presentation of models of molecules [9].These compounds can be fragments of polymermodels of optical glasses, such as «low-crownglass» and «heavyflint glass».
Results of the calculation
Optimized geometric and electronic structures, general and electronic energies of molecules3,5-di(cyclotrialumoxandiol)tetra-alumoxantetraol-1,1,7,7and 1,7-di(cyclo-trialumoxandiol)tetraalumoxantetraol-1,3,5,7 were received by method MNDO and are shown on fig. 1,2 and in tabl. 1–3. The universal factor of acidity was calculated for method MNDO by formula: рКа=42.11-147.18qmaxH+[1–8; 11] (where, qmaxH+ “ a maximum positive charge on atom of the hydrogenqmaxH+= 0.19рКа- pKa-universal index of acidity (tabl.1).рКа = 14.
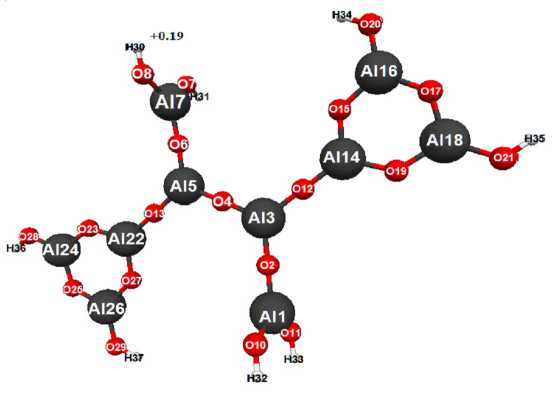
Fig.1. Geometric and electronic structure of molecule of 3,5-di(cyclotrialumoxandiol)tetraalumoxantetraol -1,1,7,7 . (Е0= -651635 kDg/mol, Еel= -3331183 kDg/mol)
Table 1
Optimized bond lengths, valence corners and charges on atoms of the molecul of 3,5-di(cyclotrialumoxandiol)tetraalumoxantetraol-1,1,7,7
|
Length of relations |
R,A |
Valent corners |
Degree |
Atom |
Charges on atoms of a molecule |
|
O(2)-Al(1) |
1.62 |
Al(1)-O(2)-Al(3) |
179 |
Al(1) |
+1.08 |
|
Al(3)-O(2) |
1.64 |
O(2)-Al(3)-O(4) |
120 |
O(2) |
-0.71 |
|
O(4)-Al(3) |
1.63 |
Al(3)-O(4)-Al(5) |
179 |
Al(3) |
+1.15 |
|
Al(5)-O(4) |
1.63 |
O(4)-Al(5)-O(6) |
120 |
O(4) |
-0.74 |
|
O(6)-Al(5) |
1.64 |
Al(5)-O(6)-Al(7) |
174 |
Al(5) |
+1.15 |
|
Al(7)-O(6) |
1.62 |
O(6)-Al(7)-O(8) |
121 |
O(6) |
-0.72 |
|
O(8)-Al(7) |
1.67 |
O(6)-Al(7)-O(9) |
122 |
Al(7) |
+1.07 |
|
O(9)-Al(7) |
1.68 |
O(2)-Al(1)-O(10) |
120 |
O(8) |
-0.55 |
|
O(10)-Al(1) |
1.68 |
O(2)-Al(1)-O(11) |
120 |
O(9) |
-0.56 |
|
O(11)-Al(1) |
1.68 |
O(2)-Al(3)-O(12) |
120 |
O(10) |
-0.56 |
|
O(12)-Al(3) |
1.64 |
O(4)-Al(5)-O(13) |
121 |
O(11) |
-0.56 |
|
O(13)-Al(5) |
1.64 |
Al(3)-O(12)-Al(14) |
179 |
O(12) |
-0.72 |
|
Al(14)-O(12) |
1.62 |
O(12)-Al(14)-O(15) |
126 |
O(13) |
-0.72 |
|
O(15)-Al(14) |
1.68 |
Al(14)-O(15)-Al(16) |
131 |
Al(14) |
+1.07 |
|
Al(16)-O(15) |
1.66 |
O(15)-Al(16)-O(17) |
110 |
O(15) |
-0.71 |
|
O(17)-Al(16) |
1.67 |
Al(16)-O(17)-Al(18) |
129 |
Al(16) |
+1.02 |
|
Al(18)-O(17) |
1.67 |
O(17)-Al(18)-O(19) |
110 |
O(17) |
-0.70 |
|
O(19)-Al(18) |
1.66 |
O(15)-Al(16)-O(20) |
125 |
Al(18) |
+1.02 |
|
O(20)-Al(16) |
1.67 |
O(17)-Al(18)-O(21) |
125 |
O(19) |
-0.70 |
|
O(21)-Al(18) |
1.67 |
Al(5)-O(13)-Al(22) |
179 |
O(20) |
-0.53 |
|
Al(22)-O(13) |
1.62 |
O(13)-Al(22)-O(23) |
126 |
O(21) |
-0.53 |
|
O(23)-Al(22) |
1.67 |
Al(22)-O(23)-Al(24) |
131 |
Al(22) |
+1.07 |
|
Al(24)-O(23) |
1.66 |
O(23)-Al(24)-O(25) |
110 |
O(23) |
-0.70 |
|
O(25)-Al(24) |
1.67 |
Al(24)-O(25)-Al(26) |
129 |
Al(24) |
+1.03 |
|
Al(26)-O(25) |
1.67 |
O(25)-Al(26)-O(27) |
110 |
O(25) |
-0.70 |
|
O(27)-Al(26) |
1.66 |
O(23)-Al(24)-O(28) |
125 |
Al(26) |
+1.02 |
|
O(28)-Al(24) |
1.67 |
O(25)-Al(26)-O(29) |
125 |
O(27) |
-0.71 |
|
O(29)-Al(26) |
1.67 |
Al(7)-O(8)-H(30) |
122 |
O(28) |
-0.53 |
|
H(30)-O(8) |
0.93 |
Al(7)-O(9)-H(31) |
123 |
O(29) |
-0.53 |
|
H(31)-O(9) |
0.93 |
Al(1)-O(10)-H(32) |
124 |
H(30) |
+0.19 |
|
H(32)-O(10) |
0.93 |
Al(1)-O(11)-H(33) |
124 |
H(31) |
+0.19 |
|
H(33)-O(11) |
0.93 |
Al(16)-O(20)-H(34) |
122 |
H(32) |
+0.18 |
|
H(34)-O(20) |
0.93 |
Al(18)-O(21)-H(35) |
122 |
H(33) |
+0.18 |
|
H(35)-O(21) |
0.93 |
Al(24)-O(28)-H(36) |
122 |
H(34) |
+0.19 |
|
H(36)-O(28) |
0.93 |
Al(26)-O(29)-H(37) |
122 |
H(35) |
+0.19 |
Table 2
Optimized bond lengths, valence corners and charges on atoms of the molecule of 1,7-di(cyclotrialumoxandiol)tetraalumoxantetraol-1,3,5,7
|
Length of relations |
R,A |
V alent corners |
Degree |
Atom |
Charges on atoms of a molecule |
|
O(2)-Al(1) |
1.63 |
Al(1)-O(2)-Al(3) |
178 |
Al(1) |
+1.11 |
|
Al(3)-O(2) |
1.63 |
O(2)-Al(3)-O(4) |
121 |
O(2) |
-0.73 |
|
O(4)-Al(3) |
1.64 |
Al(3)-O(4)-Al(5) |
170 |
Al(3) |
+1.10 |
|
Al(5)-O(4) |
1.64 |
O(4)-Al(5)-O(6) |
121 |
O(4) |
-0.74 |
|
O(6)-Al(5) |
1.63 |
Al(5)-O(6)-Al(7) |
175 |
Al(5) |
+1.10 |
|
Al(7)-O(6) |
1.64 |
O(6)-Al(7)-O(8) |
121 |
O(6) |
-0.73 |
|
O(8)-Al(7) |
1.63 |
O(6)-Al(7)-O(9) |
120 |
Al(7) |
+1.11 |
|
O(9)-Al(7) |
1.68 |
O(2)-Al(1)-O(10) |
121 |
O(8) |
-0.70 |
|
O(10)-Al(1) |
1.63 |
O(2)-Al(1)-O(11) |
121 |
O(9) |
-0.56 |
|
O(11)-Al(1) |
1.68 |
O(2)-Al(3)-O(12) |
119 |
O(10) |
-0.70 |
|
O(12)-Al(3) |
1.68 |
O(4)-Al(5)-O(13) |
120 |
O(11) |
-0.56 |
|
O(13)-Al(5) |
1.68 |
Al(1)-O(10)-Al(14) |
178 |
O(12) |
-0.56 |
|
Al(14)-O(10) |
1.62 |
O(10)-Al(14)-O(15) |
126 |
O(13) |
-0.56 |
|
O(15)-Al(14) |
1.68 |
Al(14)-O(15)-Al(16) |
131 |
Al(14) |
+1.08 |
|
Al(16)-O(15) |
1.67 |
O(15)-Al(16)-O(17) |
110 |
O(15) |
-0.71 |
|
O(17)-Al(16) |
1.67 |
Al(16)-O(17)-Al(18) |
130 |
Al(16) |
+1.02 |
|
Al(18)-O(17) |
1.67 |
O(17)-Al(18)-O(19) |
110 |
O(17) |
-0.70 |
|
O(19)-Al(18) |
1.66 |
O(15)-Al(16)-O(20) |
125 |
Al(18) |
+1.03 |
|
O(20)-Al(16) |
1.67 |
O(17)-Al(18)-O(21) |
125 |
O(19) |
-0.70 |
|
O(21)-Al(18) |
1.67 |
Al(7)-O(8)-Al(22) |
177 |
O(20) |
-0.53 |
|
Al(22)-O(8) |
1.62 |
O(8)-Al(22)-O(23) |
125 |
O(21) |
-0.53 |
|
O(23)-Al(22) |
1.67 |
Al(22)-O(23)-Al(24) |
131 |
Al(22) |
+1.08 |
|
Al(24)-O(23) |
1.66 |
O(23)-Al(24)-O(25) |
110 |
O(23) |
-0.70 |
|
O(25)-Al(24) |
1.67 |
Al(24)-O(25)-Al(26) |
130 |
Al(24) |
+1.03 |
|
Al(26)-O(25) |
1.67 |
O(25)-Al(26)-O(27) |
110 |
O(25) |
-0.70 |
|
O(27)-Al(26) |
1.67 |
O(23)-Al(24)-O(28) |
125 |
Al(26) |
+1.03 |
|
O(28)-Al(24) |
1.67 |
O(25)-Al(26)-O(29) |
125 |
O(27) |
-0.71 |
|
O(29)-Al(26) |
1.67 |
Al(5)-O(13)-H(30) |
123 |
O(28) |
-0.53 |
|
H(30)-O(13) |
0.93 |
Al(7)-O(9)-H(31) |
123 |
O(29) |
-0.53 |
|
H(31)-O(9) |
0.93 |
Al(3)-O(12)-H(32) |
123 |
H(30) |
+0.18 |
|
H(32)-O(12) |
0.93 |
Al(1)-O(11)-H(33) |
123 |
H(31) |
+0.18 |
|
H(33)-O(11) |
0.93 |
Al(16)-O(20)-H(34) |
122 |
H(32) |
+0.18 |
|
H(34)-O(20) |
0.93 |
Al(18)-O(21)-H(35) |
122 |
H(33) |
+0.19 |
|
H(35)-O(21) |
0.93 |
Al(24)-O(28)-H(36) |
122 |
H(34) |
+0.19 |
|
H(36)-O(28) |
0.93 |
Al(26)-O(29)-H(37) |
122 |
H(35) |
+0.19 |
Table 3
General energy (Е0), electronic energy (Еel), maximum positive charge on atom of the hydrogen (qmaxH+), the universal factor of acidityderivativesdioles-monomersofcationicpolymerization
|
№ |
Monomer |
Е0kDg/mol |
Е el= kDg/mol |
H+ q max |
рКа |
|
1 |
3,5-di(cyclotrialumoxandiol) tetraalumoxantetraol-1,1,7,7 |
-651 635 |
-3 331 183 |
+0,19 |
14 |
|
2 |
1,7- di cyclotrialumoxandiol) tetraalumoxantetraol -1,3,5,7 |
-651 646 |
-3 399 236 |
+0,19 |
14 |
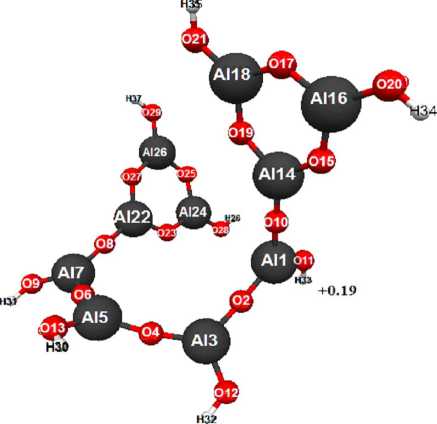
Fig. 2. Geometric and electronic structure of molecule of 1,7-di(cyclotrialumoxandiol) tetraalumoxantetraol-1,3,5,7 (Е0= -651646 kDg/mol, Еel= -3399236 kDg/mol)
Quantum-chemical calculation of molecules 3,5-di(cyclotrialumoxandiol)tetra-alumoxantetraol-1,1,7,7 and 1,7-di(cyclotrialumoxandiol)tetraalumoxantetraol-1,3,5,7 by method MNDO was executed for the first time. Optimized geometric and electronic structures of these compounds were received. Acid power of moleculesterpenes was theoretically evaluated (pKa = 14). These compounds pertain to class of very weak Н-acids (рКа = 14).
Список литературы Quantumchemical calculation of some diols by method MNDO
- Babkin V.A., Andreev D.S., Titova Е.S., Dmitriev V.U., Fomichev V.T., Zaikov G.E. Theoretical Estimation of Acidic Force of Linear Olefins of Cationic Polymerization. N. Y., Nova Publisher, 2011, 65 р.
- Babkin V.A., Andreev D.S. Quantum-chemical calculation of molecule 2-ethylbutene-1 by method MND0. Collection of research paper: Quantum-chemical calculation of unique molecular systems. Volgograd, VolGU publ., 2010, vol. 1, p. 176-185.
- Babkin V.A., Andreev D.S., Fomichev V.T., Dmitriev V.Yu. Quantum-chemical calculation of linear and branchy monomers of cationic polymerization. Volgograd, VolGU publ., 2011, 65 p.
- Babkin V.A., Andreev D.S., Titovav E.S., Sangalov Yu.А., Denisov А.А. Quantum-chemical calculation of alicyclicolefins and their derivations. Volgograd, VolGU publ., 2012, 100 p.
- Babkin V.A., Andreev D.S., Titova Е.S., Potapov S.S., Sangalov Yu.А. Quantum-chemical calculation of isoolefinsanddienes. Volgograd, VolGU publ., 2011, 71 p.
- Babkin V.A., Dmitriev V.Yu., Savin G.A., Zaikov G.E., Rakhimov A.I. Quantum-chemical aspects of mechanism acylation of bicyclophosphits by chloranhydrides of carboxylic acid. Volgograd, VolGU publ., 2011, 91 p.
- Babkin V.A., Fedunov R.G., Minsker K.S. Oxidation communication, 2002, № 1, 25, p. 21-47.
- Bode B.M., Gordon M.S., Mol J. Graphics Mod, 1998, 16, p. 133-138.
- Shmidt M.W., Baldrosge K.K., Elbert J.A., Gordon M.S., Enseh J.H., Koseki N., Matsvnaga K.A. Nguyen S.J. SU, and anothers. J. Comput. Chem. 14, 1993, p. 1347-1363.
- Вabkin V.A., Zaikov G.E. Nobel laureats and nanotechnologgy of the applaed quantum chemistry. USA. N.Y., Nova Science Publisher, 2010, рp. 351
- Babkin V.A., Dmitriev V.Yu., Zaikov G.E. Quantum-chemical calculation of molecule monomer of cationic polymerization hexene-1 by method MNDO. Collection of research paper: Quantum-chemical calculation of unique molecular systems. Volgograd, VolGU publ., 2010, vol. 1, p. 93-104.


