Работа водокольцевого компрессора с пневмопроводом

В качестве ключевого компонента мягких роботов мягкие приводы отвечают за создание движения. Были проведены исследования по поиску эффективных и систематических инструментов проектирования для различных применений мягких приводов. В работе [1] представлен метод проектирования с использованием поля главных деформаций для достижения требуемых форм в мягких исполнительных механизмах. Разработана модель исполнительного механизма, состоящая из пневматической камеры и адаптивной каркасной ограни- чительной конструкции, на основе входных данных исходной и целевой форм в предварительном моделировании. Рамная конструкция ограничивает привод в перпендикулярном направлении относительно направления растяжения в основном поле деформации. Эвристический метод использован для того, чтобы оптимизировать структуру рамки и пневматическое давление для достижения необходимой формы. Два адаптивных захвата изготовлены для проверки эффективности этого метода проектирования [1].

Мягкая робототехника обеспечивает новое решение для процессов автоматизации, которые требуют высокой гибкости и безопасного взаимодействия с человеком или тонкими объектами [2]. Мягкий пневматический привод наиболее распространенный тип приводов в мягкой робототехнике, соответственно на него растет спрос. Однако существующие методы проектирования и производства пневматических приводов часто весьма трудоемки и ресурсоемки. В работе [2] представлен новый метод оптимизации конструкции: компьютерное моделирование с использованием метода конечных элементов и модели для гиперупругого материала. Значение постоянной материала определяется на основе изучения производительности прототипа. Для проверки этого метода были изготовлены, испытаны и смоделированы пневматические приводы с различной геометрией, получены значения постоянной материала [2].

Математическое моделирование широко используется для совершенствования систем пневмотранспорта (см. [3-6] и библ. в них). Объектом изучения в данной статье является транспортная система на базе одноступенчатого водокольцевого компрессора, принципиальная схема которой показана на рис.1. Давление P o на выходе транспортной магистрали равно атмосферному P a (или близко к нему). Предельное давление на выходе водокольцевого компрессора не превышает 250 кПа. Рассматриваем условия, при которых реализуется турбулентный режим течения газа в трубопроводе; область гидравлического сопротивления в трубе - квадратичная.

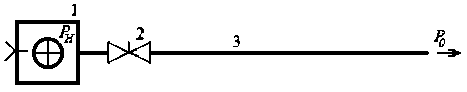
Рисунок 1 - Принципиальная схема нагнетательной системы : 1 - водокольцевой компрессор, 2 -вентиль, 3 - трубопровод

Нагрузочные характеристики водокольцевого компрессора российского производства ВК-3М1 [7] показаны на рис. 2. Приведены следующие параметры: P - абсолютное давление нагнетания кПа;, Q - производительность м³/мин; N - потребляемая мощность, кВт. В техническом паспорте имеется график производительности Q В , приведенной к давлению всасывания. Ее необходимо пересчитать на условия нагнетания. При моделировании работы водокольцевого компрессора полагают процесс сжатия изотермическим:

Q = Q b ■ ^{P 1 P} а .               ⁽¹⁾

Далее будем показывать производительность Q , пересчитанную на условия нагнетания. Экспериментальные точки на рис. 2 могут быть аппроксимированы зависимостями:

N ( P ) = A_o + A ■ P + A₂ ■ P ,

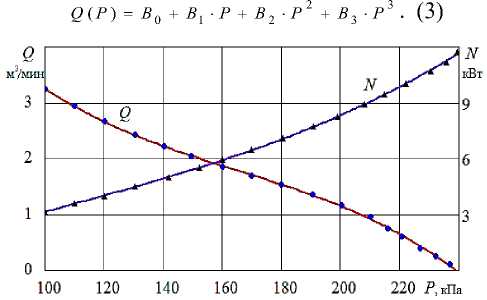
Рисунок 2 - Нагрузочные характеристики компрессора ВК-3М1 : Точки - экспериментальные данные [7], линии - расчет по (2), (3)

Для дальнейших расчетов требуется привести нагрузочные характеристики водокольцевого компрессора к безразмерной форме (рис. 3):

n(p) = v(p) = a о + a i ■ p + a 2 ■ P2 ;(4)

q = f(p) = bо + bi ■ P + b 2 ■ P2 + bз ■ P3;(5)

p = P I PA , q = Q I Qm , n = N I( PA ■ Qm ) ,(6)

где   Qm - подача при давлении нагнетания, равном атмосферному Pa . Значения эмпирических коэффициентов, найденные методом наименьших квадратов для ВК-3М1, ao = 0,378; ai = -0,156; a2 = 0,358; Ьз = -0,44. bo = 3,35; bi = -4,08; b2 = 2,17; Ьз = -0,44. Для других моделей ВКК [3] коэффициенты безразмерных характеристик отличаются незначительно.

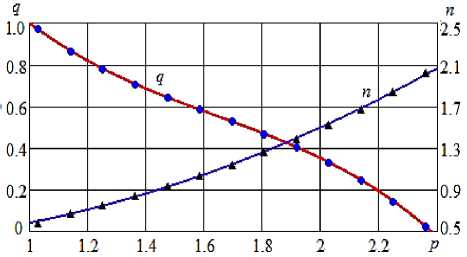
Рисунок 3 - Безразмерные нагрузочные характеристики компрессора ВК-3М1. Точки - экспериментальные данные [7], линии - расчет по (4), (5)

Баланс закачиваемого воздуха водокольцевого компрессора (кг/с):

Gh = Gb + Ge + G g ,       (7)

где    G Н = ρ Н Q Н – массовый расход ВКК;

G E – массовый расход в трубопроводе;

G B – массовый расход в окружающую среду, обусловленный нарушением герметичности;

G g – массовый расход газовыделения. Для перепадов давления, создаваемых водокольцевым компрессором, G g можно пренебречь.

Полагаем газ совершенным с уравнением состояния

P = p- R ■ t ,             (8)

где R – газовая постоянная, равная универсальной газовой постоянной, деленной на молекулярную массу;

Р – давление;

Т – термодинамическая температура газа.

Процесс в водокольцевом компрессоре близок к изотермическому, поэтому (7) можно переписать как равенство газовых потоков, используемое в вакуумной технике:

P„ ■ Q H = Q R ■ ( ^PH - ^РЛ ) + ^РЛ ■ Q F .

H  H   B  H  A   AE

В (9) использована часто применяемая гипотеза (см., например, [8]): массовый расход из-за негерметичности прямо пропорционален разности давлений в камере и окружающей среде.

При моделировании установившегося течения газа в транспортной трубе воспользуемся методом [9]. С учетом постоянства площади поперечного сечения трубы S :

G = G_e I S = p ■ W = p ■ W / ( R ■ T ) = const , W = G / p = GRT / P .         (10)

где ρ, W – средние по сечению трубы плотность и скорость газа, соответственно;

S = πD ²/4, D – диаметр трубы.

Уравнение движения (количества движения):

d W     d PW2

p W ---= ----- X p —,(11)

d X    d X2 где λ – коэффициент гидравлических по- терь на трение.

Так как длина трубы L велика ( L/D >> 100), можно не учитывать эффект начального участка, в квадратичной области сопротивления считать λ = const. Координата X направлена по оси трубы в направлении течения.

Найдем производную по координате выражения (10) с учетом T = const:

dW   GRT dP

.

d X     P2 d X

Подставим (10), (12) в уравнение (11):

^f    G ² RT ) d P     G ² RT X

1 ---= - p2 d XP

V7

Решение дифференциального уравнения

(13) с учетом условий p (0) = p_h , p ( l ) = p _a :

f

G ² RT ■   2 ■ ln

V

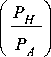
x )

+ —■ L

D

= p H - p A . (14)

где   PН – давление, создаваемое компрессо ром на входе в трубу;

P А – давление на выходе из трубы (атмосферное).

Выразим массовый расход G через объемный расход на выходе из трубы Q E :

p F ■ Q F P ■ Q F q _ ^p E e E _ A e E

S

■ S

RT

Подставим (14) в (13):

)    1   (    f P  IX

.

^P H

- PA² . (16)

V        ^V A ⁷            7

Выразим объемный расход из (15):

Q

E

■

PA

M

Q_M    W_M

S ■ Jrt" w_t ’

W

QM

, W M S

PН

P = ----,

PA

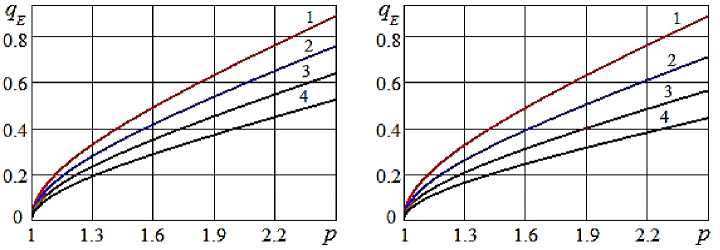
• a)                                              б)

Рисунок 4 - Зависимость безразмерного расхода на выходе из трубы от отношения давлений : а) - число Маха M = 0,5; 1 - Z = 25; 2 - Z = 35; 3 - Z = 50; 4 - Z = 75;

• б)    - коэффициент сопротивления Z = 40; 1 - M = 0,4; 2 - M = 0,5; 3 - M = 0,63; 4 - M = 0,8

Тогда балансовое уравнение (9) можно записать в следующей безразмерной форме:

p H ^{- Ч} H = k ^{- Ч} H ' ⁽ p H ^{- 1} ) +' q E •  ( ²⁰ )

Откуда

Ч е = Ч н ^{- ( (1 - k} ) ' P h + ^k ) = f ⁽ P h ) ^{- ( (1 - k} ) "  P h + ^k )

• (21)

Приравнивая выражения (18) и (21) по-

Ф ⁽ p , P , ^z ) = f ⁽ p ) - (Q - k ) ■ p + k ) • ⁽²²⁾

Решение (22) позволяет численным методом найти давление нагнетания водокольцевого компрессора в установившемся режиме при различных значениях безразмерных параметров Z, M , k . На рис. 5-8 представлены результаты расчетов.

лучим уравнение относительно давления нагне- тания водокольцевого компрессора:

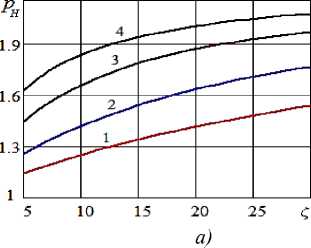
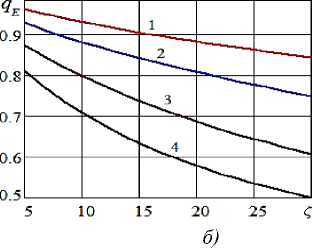
Рисунок 5 - Зависимость безразмерного давления нагнетания водокольцевого компрессора ( a ) и расхода в трубе ( б) от коэффициента гидравлического сопротивления при коэффициенте утечки к = 0,2 и различных значениях числа Маха : 1 - M =0,25; 2 - M =0,35; 3 - M =0,5; 4 - M =0,65

а)                                              б)

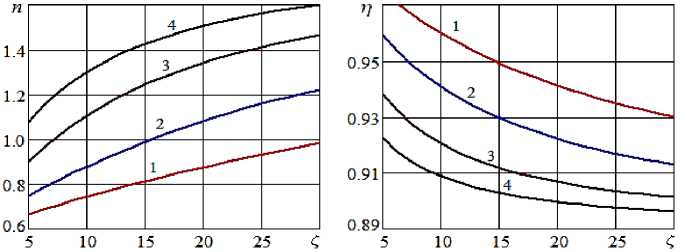
Рисунок 6 - Зависимость безразмерной затраченной мощности водокольцевого компрессора ( a ) и объемного КПД ( б) от коэффициента гидравлического сопротивления при коэффициенте утечки к = 0,2 и различных значениях числа Маха : 1 - M =0,25; 2 - M =0,35; 3 - M =0,5; 4 - M =0,65

Безразмерная затраченная мощность в установившемся режиме найдена по выражению (4): n = ^(рн). Отношение подачи водокольцевого компрессора к расходу газа в трубе (приведенного к условиям нагнетания в техни- ке называют объемным КПД) рассчитано по формуле, следующей из (20):

Ph • Чн ^{- k -} Чн A Ph ^{- 1})   ,   , f,      ¹  )

П = -------------------------------------= 1 - k -11 ------ •

Ph ^- Ч н                   ( Ph J

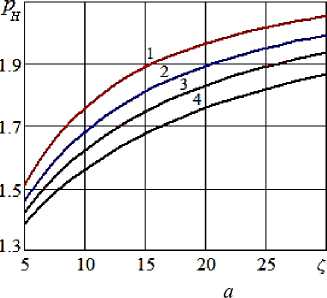
Рисунок 8 - Зависимость безразмерного давления нагнетания водокольцевого компрессора ( a ) и расхода в трубе ( b ) от коэффициента гидравлического сопротивления при числе Маха M = 0,5 и раз-

личных значениях коэффициента утечки: 1 – k = 0; 2 – k = 0,15; 3 – k = 0,3; 4 – k = 0,5

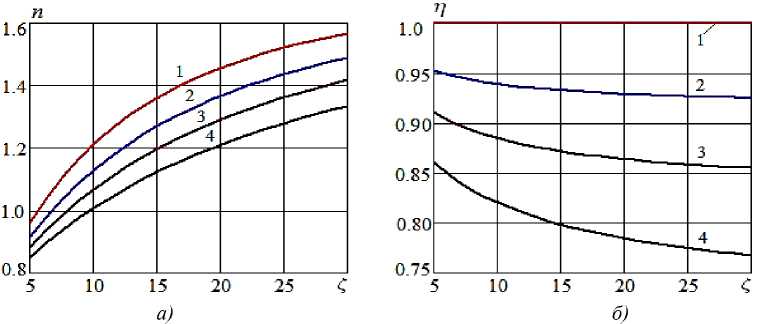
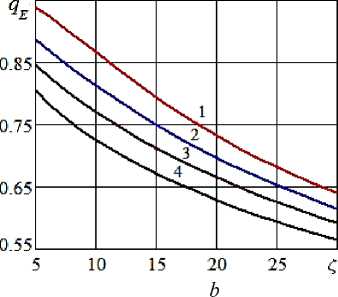
Рисунок 8 - Зависимость безразмерной затраченной мощности водокольцевого компрессора ( a ) и объемного КПД ( б) от коэффициента гидравлического сопротивления при числе Маха M = 0,5 и различных значениях коэффициента утечки: 1 – k = 0; 2 – k = 0,15; 3 – k = 0,3; 4 – k = 0,5

Во всех случаях при увеличении гидравлического сопротивления (в частности, при увеличении длины трубы) происходит повышение давления нагнетания водокольцевого компрессора и, как следствие, снижение расхода подаваемого газа и объемного КПД, повышение затраченной мощности

Как и следовало ожидать, объемный КПД η существенно снижается при увеличении коэффициента утечки k (рис. 8 b ) (в меньшей степени на него влияет изменение числа Маха (рис. 6 b )), при этом расхода подаваемого газа падает (рис. 7 b ).