Рациональный выбор параметров пространственной схемы армирования композитов

Углерод-углеродные композиционные материалы (УУКМ) активно изучаются в последнее время как перспективные материалы для тяжелонагруженных тормозных систем [1,2]. Проектирование узлов трения из УУКМ невозможно без экспериментального моделирования [1], основанного на теории трения и усталостного износа. Вместе с тем для выбора наиболее подходящей для конкретного случая пространственной схемы армирования тормозного диска представляется разумным привлечение вычислительного эксперимента, что особенно важно из-за высокой стоимости УУКМ.

Температура на поверхностях трения и напряженно деформированное состояние (НДС) тормозного диска в тонком приповерхностном слое являются важными факторами, влияющими на интенсивность износа. При упругом контакте микронапряжения £,;, определяемые на масштабном уровне порядка микрона, являются линейными функциями макронапряжений о9:

'fl~ Syfci’Gkl .                                      (1)

Для нахождения функций 8уи должна быть поставлена задача микромеханики с учетом реальной микрогеометрии поверхности и структуры материала на глубине в несколько поперечных размеров волокон. Макронапряжения же ау можно найти из решения осредненной квазистатической задачи термоупругости со сглаженной границей. Нестационарное поле температур вычисляется из численного решения задачи теплопроводности

В данной работе рассматривается тормозной диск из УУКМ с аксиально-радиально-окружной схемой армирования, при которой армирование производится по координатным линиям цилиндрической системы координат. Особенностью данной схемы является то, что объемное содержание арматуры зависит от радиальной координаты, поэтому в качестве параметров схемы взято количество волокон по направлениям в ячейке периодичности на внутреннем радиусе. Эффективные физикомеханические характеристики прогнозируются по свойствам трансверсальноизотропных армирующих волокон и изотропной углеродной матрицы при различных температурах [3] как функции радиальной координаты и температуры. Сравнение термоупругих констант, рассчитанных для ортогонально армированного композита с помощью асимптотического метода осреднения из решения задачи на ячейке периодичности и приближенным методом усреднения жесткостей, показало, что значения модулей Юнга, коэффициентов Пуассона и коэффициентов линейного температурного расширения (КЛТР) практически совпадают, а для модуля сдвига метод усреднения жесткостей дал немного завышенные значения [4]. Поскольку объемное содержание арматуры и ее распределение по направлениям изменяется в зависимости от радиальной координаты, для вычисления эффективных характеристик используем более простой метод усреднения жесткостей [5,6].

В рамках этого метода пространственно армированный композит рассматривается как совокупность однонаправленных расчетных элементов (ОРЭ), представляющих собой прямое волокно, окруженное матрицей. Считается, что объемное содержание волокна в ОРЭ равно объемному содержанию волокна в рассматриваемом объеме. Предполагается, что группы ОРЭ полностью занимают объем композита и не взаимодействуют друг с другом. Свойства отдельного ОРЭ определяются по формулам для однонаправленного волокнистого композита, а затем преобразуются к системе координат, связанной с диском. Таким образом, получаем неоднородную среду с количеством компонентов, равным количеству направлений. Окончательно эффективные характеристики рассчитываются осреднением свойств этой неоднородной среды по правилу смеси, а КЛТР находятся по методике [6].

Решение для тела с эффективными термоупругими и теплофизическими свойствами производилось методом конечных элементов (МКЭ) в осесимметричной постановке с линейными кольцевыми элементами с прямоугольным треугольником в меридиональном сечении. На верхнем и нижнем основаниях диска, где происходит трение, задаются давление и мощность тепловыделения, линейно зависящие от угловой скорости вращения, коэффициента трения, расстояния до оси вращения и давления, остальные поверхности диска считаются свободными, с конвективным теплообменом. В ходе решения на каждом шаге по времени находится нестационарное поле температур, а затем с использованием полученного поля температур решается термоупругая задача в статической постановке. В результате численного решения краевой термоупругости задачи получаем поля макронапряжений и макродеформаций.

Подбор параметров армирования производится путем решения последовательности квазистатических термоупругих задач с одинаковыми граничными условиями, но с различными параметрами схемы армирования.

При сравнении тензоров макронапряжений, полученных в результате решения краевых задач для различных расчетных схем, необходимо иметь какой-то критерий, который бы учитывал зависимость физико-механических свойств УУКМ от схемы армирования в окрестности той точки, где значение критерия оказалось максимальным. Поэтому целесообразно вычислять компоненты тензора напряжений с ° на уровне ОРЭ и сравнивать критериальные выражения, в которые входят именно эти напряжения.

По компонентам тензора деформаций ОРЭ е”. получаемым преобразованием тензора макродеформаций в оси, связанные с ОРЭ, с использованием эффективных свойств ОРЭ, вычисляемым по известным формулам.

В качестве критериев в данной работе выбраны отношения четырех инвариантов НДС для трансверсально изотропного материала к соответствующим прочностям с учетом знака нагрузки, характеризующих нагруженное состояние по различным типам возможного разрушения: Л - на продольный отрыв, Л - на поперечный отрыв, J3 - на продольный сдвиг и Л - на поперечный сдвиг:

ст11 Ст” / „ °22+Сз:

или

2S"'

— или -—, -    -

О] 1         01 1            ^00?

J                J ^ У(<722-Озз)²+4(5У

3           лО         ’    4                лО              ■

°12                       °23

Последовательность задач решается до тех пор, пока не подбирается схема армирования с минимальным значением максимального из инвариантов. В качестве примера, иллюстрирующего данную методику, рассмотрим подбор схемы армирования для диска с высотой Н = 0,02м, внутренним радиусом 7?о=О, 1м и внешним радиусом А1=0,Зм при следующих параметрах нагружения: начальной угловой скоростью <ау=100 с'¹, времени до полной остановки Г=25 с, давлении на поверхнотсь Р = 0,2 МПа и коэффициентом трения // = 0,4. Считается, что диск вращается равнозамедленно На рис. 1-6 изображены зависимости от времени для максимальных по объему значений двух наибольших инвариантов и характерное расположение зон максимальных значений на меридиональном сечении диска при исходной схеме армирования с отношением на внутреннем радиусе 1:1:1 и плотной упаковкой.

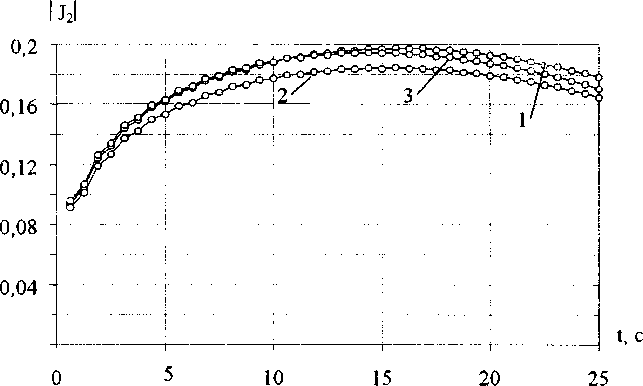
Рис. 1. Максимальные по объему значения инварианта на поперечный отрыв для ОРЭ: 1 - радиального, 2 - аксиального и 3 - окружного направлений

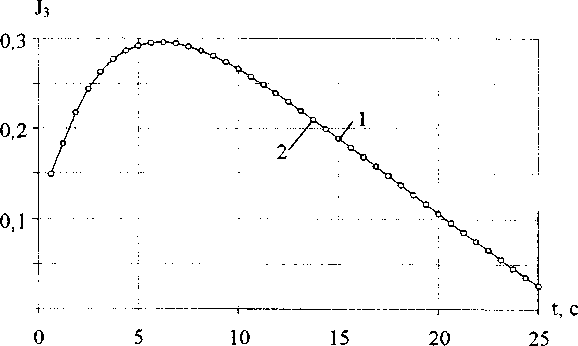
Рис.2. Максимальные по объему значения инварианта на продольный сдвиг для ОРЭ: 1 - радиального, 2 - аксиального напоавлений

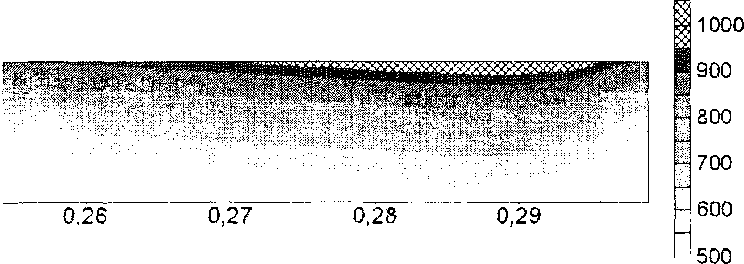
Рис.З. Распределение температуры ио меридиональному сечению диска в момент времени Z=10 с. Изображена верхняя симметричная часть сечения

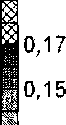
0,26         0,27         0,28         0,29

0,11

0,09

0,07

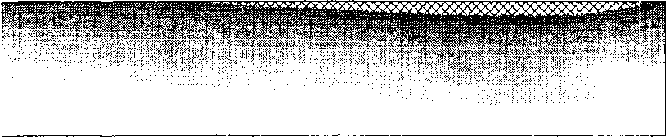
Рис 4 Распределение значений инварианта Л для ОРЭ радиального направления по меридиональному сечению диска в момент времени /= 10 с. Изображена верхняя симметричная часть сечения

0,26         0,27         0,28         0,29

Рис.5. Распределение значений инварианта Л

0,00

для ОГ‘Э радиального направления по меридиональному сечению диска в момент времени /=10 с

Изображена верхняя симметричная часть сечения

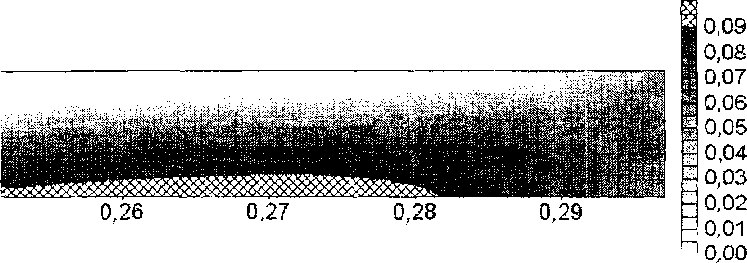
Рис. 6. Распределение значений инварианта J^ для ОРЭ осевого направления по меридиональному сечению диска в момент времени /=10 с Изображена верхняя симметричная часть сечения

Для данного случая из всех опробованных схем наилучшей оказалась схема с отношениями армирования 1:1:24, где первый коэффициент соответствует радиальному направлению, второй окружному, а третий осевому. Кроме отношений армирования существенное влияние на свойства оказывает форма поперечного сечения пучка. Так, пучок из 24 волокон осевого направления может иметь разную форму, что влияет на размеры ячейки периодичности и, следовательно, на объемные содержания волокон и свойства среды. В данном случае подобрано отношение 8:3, где первый коэффициент определяет размер сечения в радиальном направлении, а второй - в окружном. Результаты расчетов по данной схеме даны на рис.7-9. Как видно из графиков, изменением схемы армирования удалось существенно снизить значения рассматриваемых инвариантов.

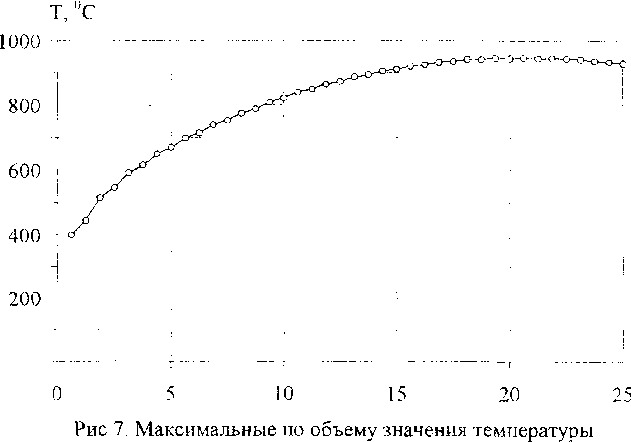
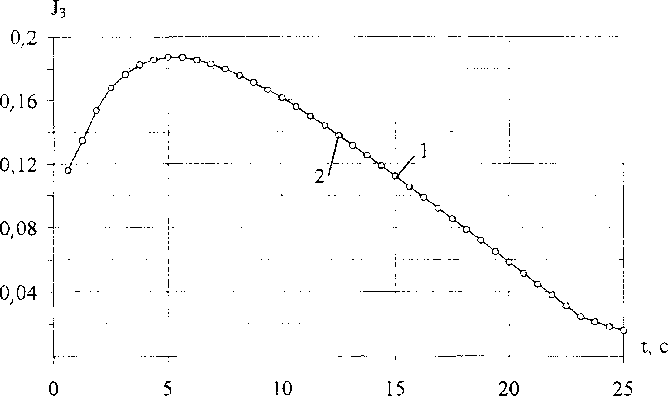
Рис. 8. Максимальные по объему значения инварианта на продольный сдвиг для ОРЭ: 1 - радиального, 2 - аксиального направлений

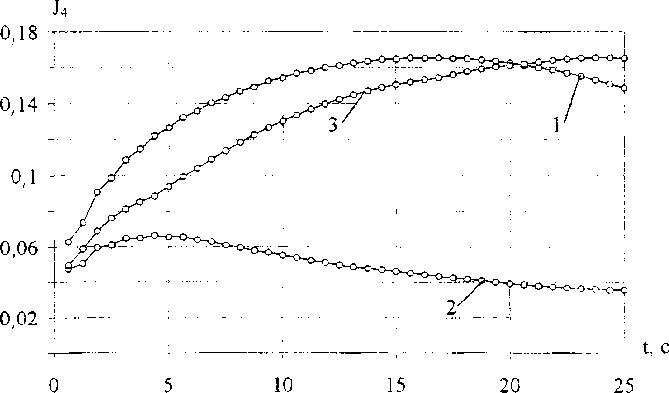
Рис.9. Максимальные по объему значения инварианта на поперечный сдвиг для ОРЭ: 1 - радиального, 2 - аксиального и 3 - окружного направлений

Для анализа влияния режима нагружения были подобраны параметры для диска таких же размеров, но при следующем нагружении: скоростью одг=100 с"¹, временем до полной остановки /=50 с, давлением на поверхность Р = 0,1 МПа и коэффициентом трения ц = 0,4. Этот режим характерен тем, что при нем диском поглощается то же количество энергии, вычисляемое по формуле (2), W=5,45-10⁶ Дж; что и при предыдущем, но максимальная мощность тепловыделения на поверхности по формуле (3) в два раза меньше, в первом случае у_тах = 1,2-10⁶ Вт/м², а во втором у/_тах = 0.6-10⁶ Вт/м²,

Vmax^^PRl- (4)

Для второго случая была подобрана схема армирования со следующими параметрами 1:1:(2:6), где 2:6 - отношение размеров сечения пучка в осевом направлении. Графики для этого случая даны на рис. 10-12.

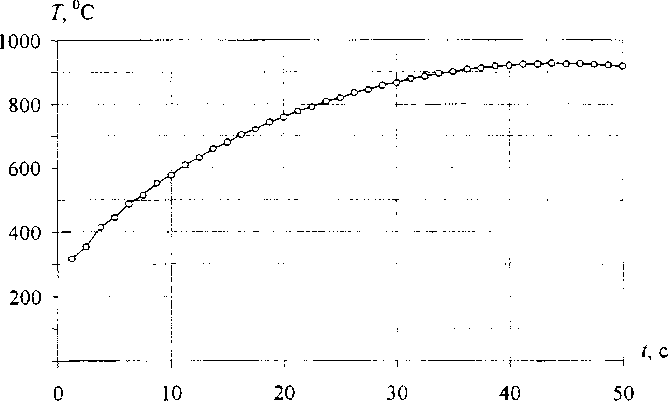
Рис. 10. Максимальные по объему значения температуры

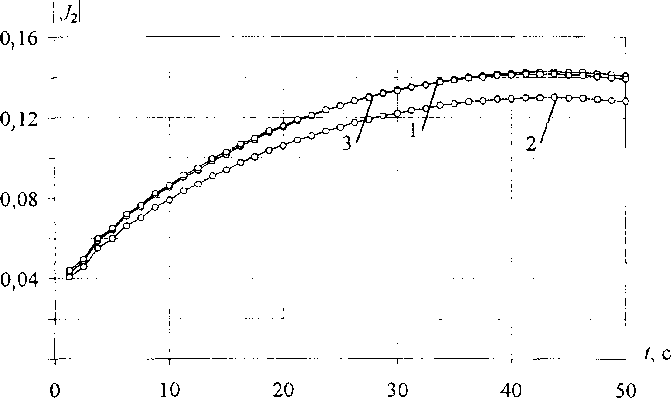
Рис. 11. Максимальные по объему значения инварианта на поперечный отрыв для ОРЭ: 1 - радиального, 2 - аксиального и 3 - окружного направлений

При сравнении двух приведенных случаев подбора схемы армирования для диска можно отметить, что основное влияние на выбор схемы армирования оказывает не температура в диске, а интенсивность процессов тепловыделения на поверхности, при этом определяющим оказывается количество волокон в осевом направлении, так как именно в этом направлении возникают наибольшие тепловые градиенты, а теплопроводность вдоль волокна, как минимум, на порядок превышает теплопроводность матрицы и теплопроводность поперек волокон.

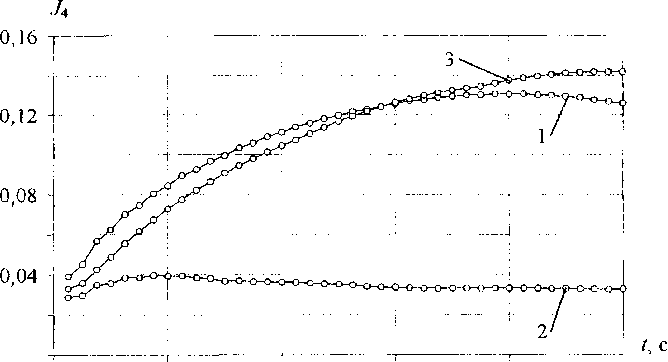
О          10         20         30         40         50

Рис. 12 Максимальные по объему значения инварианта на поперечный сдвиг для ОРЭ: 1 - радиального, 2 - аксиального и 3 - окружного направлений

Работа выполнялась при поддержке РФФИ (грант 98-01-00996) и Министерства образования РФ (грант 98-10-1.1-41 по фундаментальным исследованиям в области транспортных наук).