Рациональный выбор структур и конфигураций неоднородных вычислительных систем при помощи эволюционного поиска

С каждым годом усиливается роль информационно-вычислительных систем в укреплении обороноспособности страны, в решении хозяйственных и научных задач. При этом особое звучание приобретают вопросы совершенствования средств вычислительной техники, автономно решающих задачи в режиме реального времени в сложных условиях функционирования, которые характеризуются как воздействием множества внешних факторов, так и спектром различных режимов функционирования. Таким образом, вычислительные системы (ВС) рассматриваемого класса вынужденно функционируют в меняющихся условиях внешней среды и управляющих воздействий [1].

Современные технологии, связанные с развитием электронной компонентной базы и коммуникационных стандартов, создают предпосылки к совершенствованию архитектуры ВС, а современная элементная база сегодня позволяет осуществлять гибкое управление режимами работы с учетом производительности, энергоемкости, температурного режима и других условий. Поэтому совершенствование ВС связано с конвергенцией их информационно-вычислительных ресурсов в единую много-

функциональную вычислительную систему с единым программным управлением и гибким выбором режимов работы компонентов, обладающую сложной неоднородной иерархической структурой.

Однако традиционные методы анализа и синтеза ВС не позволяют в полной мере реализовывать указанные преимущества. Принципиальные особенности ВС указанного класса требуют учета разнообразия элементов, многообразия их возможных состояний, а также неоднородности связей в системе как на одном, так и на разных уровнях иерархии. Кроме того, классические вероятностные подходы теории надеж- ности и живучести имеют такие недостатки, как сложность учета взаимовлияния воздействующих факторов (ВФ); зависимость оценок от параметров всех ВФ, которые нужно знать априори; характер получаемых оценок, как правило, недостаточно адекватно отражает динамику функционирования системы в конкретных условиях [2].

Подход к моделированию функционирования ВС

Суть ресурсного подхода к построению модели ВС в условиях структурнопараметрической деградации [3], расширяющего понятие ресурса применительно к различным физическим процессам, состоит в следующем. Пусть элемент системы имеет некоторые ресурсы (случайные, детерминированные), позволяющие выдержать определенные виды воздействий и реализовать свое качество. При функциони- ровании ресурсы расходуются, и по израсходовании одного из них наступает отказ. Это время зависит от динамики характеристик ВФ и режимов работы, и от случайной, в общем случае, величины запаса ресурса элемента.

Пусть в момент времени t некоторый элемент системы Zi характеризуется вектором выработанного ресурса ri (t) = < r^1 (t),...,rL)(t)> и запасом ресурса u_ = < ^1,_,uiL) >, любые компоненты которого могут быть стохастическими либо детерминированными. В общем случае запас ресурса может изменяться в процессе dr! (t)

функционирования системы. Расход ресурса элемента---— в данный момент вре- dt --*

мени зависит от его выработанного ресурса r ( t ) , его режима работы с. и воздействия ----*

на него среды (вектора параметров ВФ hi , который задается законами распределения dr(j) (t)            T Г либо является детерминированной величиной): ----— = о(j) r(j),с., h . Соответ- dt ii ii ственно, выработанный элементом Zi ресурс к моменту t + At составит t+A t rj)(t + At) = r(j)(t)+ j 8(j)(r(j)(T), ci (T), w,(T)) dт, а работоспособность элемента можно выразить при помощи функции Хевисайда от si (t) = П>(uj) - rj)(t)).

остаточного ресурса:

Будем считать [3], что элементами структуры ВС являются процессоры, запоминающие устройства и каналы обмена, а связи заданы в виде матрицы смежности. Состояния элементов описываются вектором текущих значений параметров: быстродействия, доступного объема памяти, пропускной способности, потребляемой электрической мощности, интенсивности перемежающихся отказов. Уровни иерархического объединения компонентов описываются в виде множеств и матриц смежности компонентов соответствующего уровня иерархии. Конфигурация ВС определяет множество схем резервирования, режимы работы элементов и матрицу распределения задач. Задано множество задач, решаемых ВС, каждая из которых характеризуется директивным сроком выполнения, множеством необходимых для ее решения элементов структуры и следующими параметрами: объемом вычислений, требуемым объе-

Серия «Сложные системы …». Выпуск 1

мом памяти, объемом данных для обмена с памятью, объемом данных для передачи внешним абонентам. Определены правила формирования схемы решения и оценки качества решения задач, параметры которых определяют ограничения по суммарному быстродействию, пропускной способности и объему памяти элементов.

Необходимо указать, что сложность учета внешних воздействий в различных режимах функционирования элементов системы, а также частных показателей целевого эффекта ведут к существенному усложнению целевой функции, вычисление которой сводится, по сути, к процессу имитационно-аналитического моделирования.

Поиск рациональной структуры ВС

Классический подход при решении задач синтеза ВС состоит в последовательном выборе архитектуры системы на основе качественного анализа существующих вариантов, формализации выбранного типа структуры и параметрического синтеза ее компонентов [4] при помощи известных методов оптимизации. Однако возникающая задача комбинаторной оптимизации имеет ряд сложностей, прежде всего – необходимость поиска глобального экстремума стохастической целевой функции, что ведет к серьезным затруднениям в использовании широко известных математических методов и требует специальных подходов, среди которых выделяются методы эволюционного поиска [5].

Эволюционное моделирование выступает мощным инструментом приближенного решения сложных комбинаторных задач оптимизации. Преимущества методов оптимизации на его основе в сравнении с классическими состоят, прежде всего, в возможности различных способов задания целевой функции и типов переменных оптимизации; одновременном анализе множества вариантов системы из различных областей пространства решений; вероятностных, а не детерминированных, правил поиска и генерации решений. Генетическими алгоритмами [6] называют способы решения задач оптимизации на базе эволюционного моделирования, основанные на использовании аналогий с природными процессами естественного отбора. Они достаточно глубоко развиты, но, тем не менее, значимыми нетривиальными вопросами реализации в конкретных случаях являются построение целевой функции и формализация переменных оптимизации в пространстве возможных решений, что в рассматриваемом случае требует учета особенностей кодирования сложной гетерогенной структуры.

Суть метода обоснования выбора структуры ВС на основе генетического алгоритма состоит в следующем. Задается целевая функция как скалярный показатель качества ВС. Целесообразна фильтрация возможных типов элементов в подмножество с неулучшаемыми значениями их частных показателей качества. Далее проводится формализация структуры ВС и ее кодирование в виде «хромосомы» (пример схематично представлен на рис. 1).

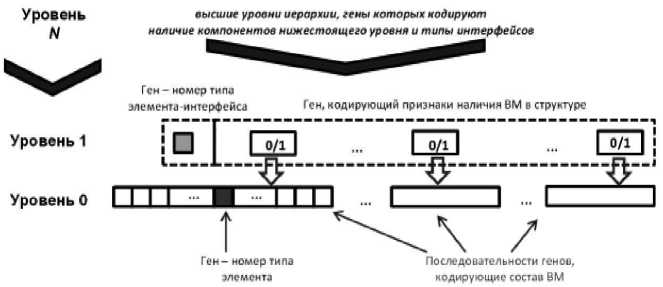
Рис. 1. Схема кодирования вариантов структуры ВС

Затем формируется исходная популяция, содержащая P случайно сгенерированных хромосом и хромосом, соответствующих специфическим точкам пространства решений. Осуществляется настройка параметров поиска: размера популяции P, влияющего на трудоемкость поиска; параметра кроссинговера R, определяющего степень детализации поиска в локальных областях пространства решений; параметра мутации M, определяющего степень исследования в новых областях пространства решений; критерия селекции G, определяющего характер отбора лучших хромосом для формирования нового «поколения». В основе метода лежит итерационная реализа- ция эволюционного поиска, включающего последовательное применение оператора кроссинговера, оператора мутации, нормализацию формального описания генотипа, вычисление fitness-функций Ψ и применение оператора селекции в каждой итерации, соответствующей поколению. Поиск завершается при достижении заданного числа поколений или снижения скорости сходимости алгоритма, а в качестве результата принимается хромосома S из последнего поколения, имеющая максимальное значение fitness-функции Ψ(S).

Приведем до статочно простой пример исследования работы алгоритма. Пусть ВС с архитектурой общей шины может включать до n вычислительных модулей (ВМ) четырех типов с быстродействием ν _i ∈ <25; 12; 15; 20>, энергопотреблением ε _i ∈ <2; 1; 3; 6>, массогабаритным показателем γ _i ^∈ <10; 2; 3; 5> и интенсивностью отказов λ _i ∈ <0,2; 1,0; 0,5; 0,1> в условных единицах ( i – номер типа ВМ). Целевую

Tn

E

n

, ∑ γ _i ≤ g , что соответству- i = 1

функцию определим как Т = JZ v , ( 1 - e ) dt , T = 0 I = 1

n ∑ ε i

i = 1

ет математическому ожиданию объема вычислений, суммарно произведенного ВМ за время исчерпания энергоресурса E при ограничении суммы массогабаритных показателей ВМ из состава ВС величиной g . Процесс работы генетического алгоритма поиска оптимального состава ВС усреднялся по 1000 запускам. Настройка параметров генетического алгоритма R = 0,05; M = 0,5; G = 50% соответствовала «случайнонаправленному» поиску, настройка R = 0,4; M = 0,05; G = 25% – «направленнослучайному», при этом P = 8. Так, пример для n = 20; g = 100 ; E = 200 показал достижение максимума в десятки раз быстрее полного перебора по количеству вычислений целевой функции. Пример для n = 9; g = 50; E = 120 продемонстрировал, что варьирование параметров настройки алгоритма может служить для поиска локальных экстремумов и принятия оптимально-компромиссного решения. В целом статистическое исследование [7] работы алгоритма на относительно простых примерах показало следующее. Целесообразность применения предложенного подхода резко возрастает с ростом размерности задачи: количество вычислений целевой функции для достижения оптимума снижалось в 3-4 раза при n = 10 и в десятки раз при n = 20 по сравнению с полным перебором. Количество вычислений целевой функции, потребовавшееся для достижения ее 85–90% приращения относительно случайного решения и максимума, оказалось ниже еще в 2-3 раза. Настройка параметров генетического алгоритма показала, что их варьирование может служить основой для поиска локальных экстремумов: «направленно-случайные» варианты настройки с высокой вероятностью оператора кроссинговера и низкой вероятностью оператора мутации показали гораздо большую скорость сходимости, однако для ряда наборов исходных данных «случайно-направленные» варианты привели к решениям, более близким к оптимальному по значению целевой функции.

Выбор конфигураций ВС при автономном управлении ее функционирова- нием

Суть функционирования ВС можно представить как расходование ею своих ресурсов в обмен на выполняемую вычислительную работу (целевой эффект) и в резуль-

Серия «Сложные системы …». Выпуск 1

тате внешних воздействий. Таким образом, задача автономного управления сводится к отысканию оптимального в смысле некоторого критерия управления при условии, что известны законы распределения случайного запаса ресурса элементов системы и параметров ВФ [8]. Ключевую роль в декомпозиции и решении данной задачи играет то, что отказы элементов, т.е. скачкообразные изменения характеристик системы, во-первых, происходят в случайные моменты времени, а во-вторых, требуют коррекции управления. Таким образом, задача рационального выбора режима функционирования ВС на некотором интервале заключается в поиске решения с учетом того, что качество функционирования системы на последующих интервалах времени зависит от того, как изменилось состояние системы и какой ресурс выработан на данном интервале.

Под функционально-параметрическим конфигурированием ВС будем понимать определение состава работающих ВМ и комплекса выполняемых задач на основе прогнозирования состояния ее аппаратуры для максимизации целевого эффекта за срок активного существования. Точное решение данной задачи путем динамического программирования может оказаться неприемлемо трудоемким. Поэтому предложим идею решения этой задачи посредством генетического алгоритма. Определяющее достоинство предложенного подхода для построения алгоритмов автономного управления ВС заключается в том, что в условиях высоких требований к оперативности решения задачи управления высокой вычислительной сложности и ограниченных возможностях бортовых вычислительных средств, с учетом необязательности точности и гарантированности достижения экстремума целевой функции он обладает высокой скоростью сходимости алгоритма.

При решении данной задачи в качестве значений «генов» будут выступать переменные, соответствующие режимам функционирования элементов ВС. При этом сложность задачи целесообразно упростить за счет построения детерминированных зависимостей режимов работы элементов вышестоящих уровней от состояний и режимов агрегируемых элементов. Кроме того, задача существенно упрощается в случае бинарного характера работы (например, включен или выключен, активный или пассивный режим и т.п.) элементов ВС.

Заключение

Достоинства предложенного подхода к приближенному решению сложной комбинаторной оптимизационной задачи большой размерности за счет применения аппарата эволюционного моделирования позволяет обосновать рациональный выбор сложных неоднородных структур вычислительных систем и их конфигураций с учетом максимизации целевого эффекта за срок существования. Предложенный способ решения задачи структурно-параметрической оптимизации представляется целесообразным при обосновании технического облика ВС и построения алгоритмов автономного управления их функционированием.