Радиационное давление на включения с заданной амплитудой рассеяния в поле первичных плоских волн

Использование ультразвука получило широкое применение в интересах решения современных научных и прикладных проблем. Одним из важных аспектов применения ультразвука является его использование в вопросах акустического расслоения, где существенную роль играют радиационные силы, приводящие к смещению частиц, взвешенных в среде [1–5 и др.]. Вопросам расчета радиационных сил на частицы, помещенные в поле звуковой волны в идеальной и неидеальной жидкостях, посвящен достаточно обширный круг работ. Сошлемся лишь на некоторые из них [6– 13]. Как правило, рассматривается действие радиационных сил на единичные мелкие частицы с размерами, много меньшими длины волны. В работах [8, 12, 13] рассматриваются силы радиационного давления, действующие на сферически симметричные рассеиватели произвольных размеров. В работе [11] рассматривается продольная сила, действующая на длинный цилиндр малого диаметра, ориентированный параллельно фронту падающей волны. Однако в ряде случаев вследствие таких процессов, как агглютинация, необходимо рассматривать воздействие радиационного давления на произвольно ориентированные конгломераты связанных между собой частиц, суммарный размер которых может быть сравним или больше длины волны, а совокупная форма не обладает сферической либо цилиндрической симметрией [14].

Из всех типов волн, для которых изучается радиационное давление, повышенное внимание уделяется плоским бегущей и стоячей волнам. Связа- но это не только со сравнительной простотой задачи, но и с важностью этих типов падающего поля. Многие типы волн, такие как сферическая, цилиндрическая, гауссов пучок и т. д., в волновой зоне становятся по фронту близкими к плоским. Поэтому важно правильно рассчитывать радиационное давление в плоской бегущей и стоячей волнах, в том числе и на сложных включениях с заданной амплитудой рассеяния.

ПОСТАНОВКА ЗАДАЧИ

В настоящей статье, являющейся обобщением работы [15], рассматриваются силы радиационного давления для идеальной жидкости в поле бегущей и стоячей плоских волн, действующие на конгломераты идентичных, соединенных друг с другом малых по сравнению с длиной волны сферически симметричных частиц. Все компоненты сил радиационного давления рассчитываются через совокупную амплитуду рассеяния конгломерата частиц. Для этого вначале задача решается для включения с амплитудой рассеяния, заданной в общем виде, затем приводятся компактные выражения для сферически симметричных включений и, наконец, получаются выражения для радиационного давления, действующего на конгломераты одинаковых сферических частиц.

РЕШЕНИЕ ПРОБЛЕМЫ

Рассмотрим однородную среду, заполненную идеальной жидкостью с плотностью ρ и скоро- стью звука c . Пусть далее в начале координат находится включение, заданное амплитудой рассеяния f (θ,ϕ) . Рассмотрим гармонические акустические волны с фактором e-i™t, далее опускаемым. Поле акустического давления состоит из суммы произвольной падающей и рассеянной волн p = Рте + Ps. Поле рассеяния в волновой зоне связано с амплитудой рассеяния и определяется выражением

рассеивателя, находящегося внутри этой поверхности интегрирования.

Как видно, квадратичная составляющая силы (3) связана с амплитудой рассеяния. Свяжем и выражение для перекрестной составляющей (2) с амплитудой рассеяния включения. Для этого рассмотрим разложение произвольной амплитуды рассеяния f ( θ , ϕ ) в ряд по сферическим функциям [16]

/ a a f(⁹,ф ) fa          т

P s ( r,9,ф ) = ----- e k ^rkr .            (1)

r

Здесь f ( 9 , ф ) — амплитуда рассеяния в произвольном падающем поле; ( r , θ , ϕ ) — сферические координаты точки наблюдения; рассеиватель находится в начале координат.

Сила радиационного давления в случае произвольного падающего поля в квадратичном приближении может быть представлена в виде суммы двух отличных от нуля слагаемых: перекрестного слагаемого с входящими в него первичным и рассеянным полями, а также слагаемого, квадратичного по рассеянному полю [9]. Рассмотрим вклад обоих слагаемых. Перекрестное слагаемое (индекс is ) определяется выражением [9, 10]

to f (9,Ф) = £

1 = 0

A ⁰ P (cos 9 ) +

l

+ ^ [ A lm cos тф + B lm sin тф J P lm (cos 9 )

m = 1

где коэффициенты равны

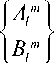
2 1 + 1    ( 1 - m )!

2 n (1 + S o m )( 1 + m )! ^X

π 2π xj 1 f (9, ф)Pim (cos 9)

cos mϕ sin mϕ

sin θ d θ d ϕ .

(4а)

F i⁽ is ) = ^{- Р} 1 ( v n' ^{( x )} (^{А + k 2} ) ф s * ^{(x ) +} к ^.с. ) ^d V =

4 _V

= 7- 1? J Р p in ^(x) ( А + k ² ) P s * ( x ) + к.с. 1 d V ,    (2)

4 pro2 V ( dx,                         J а слагаемое, квадратичное по рассеянному полю (индекс ss ) легко может быть выражено в терминах амплитуды рассеяния в волновой зоне из выражений работы [9]

— ( ss )        1          ,2

F i = -? ^P 1 I v s I cos ⁹ i ^{d 5} =

2 _S

= -1^7 J $\ f ( 9 , Ф )| ² cos 9 , sin 9 d ф d 9 , i = 1,3.   (3)

2 ρc ² _{0 0}

Здесь δ _{0 m} — символ Кронекера.

Известно [17], что вне рассеивателя совершенно идентичное поле может быть создано системой мультиполей, сосредоточенных в одной точке внутри рассеивателя. Свяжем эту систему мультиполей с амплитудой рассеяния. Для этого будем почленно дифференцировать тождество

ikr

(А + k2) — = -5( x )S( y )S( z)(5)

4πr с помощью оператора f Sa da2 da3 )। ।

=      ,,,    a i = a + a + a ; a

(axa' ’aya2 dza3 J      1 1     1     23

натуральные числа; r = ^x2 + y2 + z2 . Из урав нения (5) в результате имеем

Здесь v_i , ϕ — компоненты колебательной скорости и ее потенциал; cos θ_i — направляющий косинус радиус-вектора точки на сфере относительно i -й оси координат cos 9 1 = sin 9 cos ф , cos 9 2 = = sin 9 sin ф , cos 9 ₃ = cos 9 ( i = 1 — x -координата, i = 2 — y -координата, i = 3 — z -координата).

Выражение для квадратичной составляющей в форме (3) является следствием неизменности импульса в любом объеме идеальной жидкости, не включающем рассеиватель. Это позволяет отнести поверхность интегрирования бесконечно далеко от

( А + k ² ) D ^a | e k- | = - D ^a ( S(x)S(y)S(z ) ) = ( 4nr J

= - 5 ^{( a i )} ( x )5 ^{( a} 2 ) ( y )5 ^{( a} 3 ) ( z ).

Здесь - a H ( x ) = - 5 ^{( a 1 )} ( x)S ^{( a} 2 ) ( y)S ^{( a} 3 ) ( z ) — мультиполь порядка α [17], сосредоточенный в начале координат. В получившемся решении D ^а | e ikr- 1 ( 4 nr J будем удерживать только слагаемые с порядком не выше O ( r ^{- 1} ). Тогда, очевидно, дифференцировать нужно только числитель. Введем обозначение

p ( r , 0, ф ) =

D ^н ( e kr )

4 πr

ikr

= ( ik )“ ( sin 0 cos ф ) “1 ( sin 0 sin ф ) “2 cos “ ³ 0-— .   (7)

Здесь (r,0,ф) — сферические координаты точки наблюдения. Таким образом, мультиполь из (6) создает дальнее поле с амплитудой рассеяния fH (0, Ф) =

( ik ) ^н ( sin 0 cos ф ) ^н ( sin 0 sin ф ) “ ² cos “ ³ 0

=                     4 П                   •     (8)

Далее, согласно (9), (10), имеем

( A + к ² ) p_s * ^{( x )} =

= - Z C l *5 ⁽ “ 1- ) ( x ) 5 ^н 2 - ) ( y ) 5 ^н 3 - ) ( z ),        (11)

l = 0

Если теперь в (4) учесть соотношение между присоединенными функциями Лежандра и полиномами Лежандра [16]

P m (cos 0 ) = sin ^m 0

m d P(t) dtml

t = cos 0

а также воспользоваться разложением тригонометрических функций sin mϕ , cos mϕ кратных аргументов через различные степени функций однократного аргумента, то легко видеть, что амплитуда рассеяния (4) может быть представлена в виде суммы (бесконечной в общем случае) взвешенных амплитуд рассеяния вида (8)

откуда из свойств интегрирования производных δ -функций следует, что существенными при интегрировании в (2) будут только такие δ -образные источники справа в (11), в которых отсутствуют производные δ -функций по координатам, отличным от i -й координаты. Это означает, что при вычислении (2) в случае бегущей или стоячей волны, перпендикулярной, например, оси z достаточно вычислять в (4) только коэффициенты Al0 , т. е. существенными будут только члены to ряда Z Al0Pl (cos 0) из разложения (4) функции l=0

f ( θ , ϕ ) . Как видно из (6), (8), этому ряду соответствует система мультиполей

5 | = - 4 п x

[ ^l /2 ]

• Z A 0 Z ( - 1)

l = 0

x 5 ( x ).

n = 0

(2l - 2 n )!     f 1 D )

2 ^ln !( l - n )!( l - 2 n )l ( ik z )

to f (0,ф) = Z Cif\H (0, ф),         (9)

l = 0

Внутренняя сумма в (12) равна р [ — | ;

I ik )

а это означает, что поле (1) формируется системой мультиполей to

5 = -£ Ci§H (x) = l=0

= - Z C l 5 ^н ) ( x ) 5 ^н 2 - ) ( y ) 5 ^н 3 - ) ( z ).        (10)

l = 0

Правомерность замены реального рассеивателя эквивалентной системой мультиполей определяется тем, что интеграл по поверхности, внутри которой находится реальный рассеиватель, определяющий перекрестную составляющую радиационного давления, совершенно идентичен для поля реального рассеивателя и для поля эквивалентной системы мультиполей. Этот интеграл для системы мультиполей сводится к объемному интегралу (2), который тем самым и определяет искомую составляющую радиационного давления.

Проанализируем перекрестную составляющую (2). Во-первых, при зависимости i -й составляющей скорости первичной волны только от одной переменной, как в случае плоской стоячей или бегущей волны, отлична от нуля только продольная составляющая ( i = 3) радиационного давления в (2).

D z =9 1 d z ; [ l /2] — целая часть l / 2.

Для получения конкретных выражений для бегущей и стоячей плоских волн примем следующие условия: p^c = p0eikz — для бегущей волны и Рте = Ро (eik(z+h) + e - ik (z+h)) = 2 p 0 cos k (z + h) — для стоячей волны, p0 = const, h = const. Тогда выражение (1) будем писать в виде

/ А X ^f ( ⁰ , ф ) p_s ( r,0,ф ) = p о -----^e^,kr ,

r

подразумевающем, что f ( 0,ф ) — соответствующая амплитуда рассеяния при p ₀ = 1. Выражение (3) в этом случае принимает вид

( ss )

Fi' =

₂ π 2 π

= -- ^j J f ( 0 , ф )| ² cos 0 , sin 0dф d 0 , i = 1,3.     ⁽¹⁴⁾

2 ρc ² _{0 0}

После подстановки (12) в (2) имеем для бегущей волны

F z⁽is ) =

4n     т л о

=  E у Im A 0 J k I=0

[ [ I /2 ]

S’-1’

(2 I — 2 n )!       I ₍₁₅₎

2 l n !( 1 - n )!( 1 - 2 n )!L     ’

p ²

Здесь E = —⁰— — средняя плотность энергии в 2 ρc ²

падающей бегущей волне. Для выражения в фигурных скобках в (15) справедливо равенство

^[^-             (2 1 - 2 n )!

\ (- 1) n ______-________-_______= 1

^S       2 l n !( I - n )!( I - 2 n )!    ,

следующее из разложения полиномов Лежандра в ряд и их свойства P_t (1) = 1, I = 0,1,2,... Тогда (15) упрощается

— (is) 4п —

Fz = —E^ Im A, 0.(16)

k    ьо‘

Для стоячей плоской волны имеем

( is )       4 π

F z =-- E st x k

to

l„

*Ш ( - 1)

1 = 0

n = 0

! 1 - n

(2 1 - 2 n )! _x 2 ¹n !( 1 - n )!( 1 - 2 n )!

/      „ v <     \ 1 - 2 n

I          - in (1 -2 n) II 1 I x Re A0 e 2      —D

I ¹         A k z J

sin k ( z + h )| _o > .

это выражение вновь в терминах амплитуды рассеяния имеет вид

F_z = E J J| f (е, _Ф )^ ( 1 - cose ) sin ede d ^ , i = i,3. (18) 00

Здесь f ( θ , ϕ ) — амплитуда рассеяния включения в поле плоской волны p^ c ( x ) = e ik . Докажем, что сумма F z⁽'s ) + F z⁽ss ) из (16) и (14) соответственно совпадает с выражением (18). Для этого, очевидно, нужно доказать равенство

F z ⁽ is ) = 4 ⁿ e ^ I_m A 0 = e jJ| f ( e , ф )|² sin e d e d ф , k 1 = 0                ^Jo^Jo'

или после сокращения

^{2 п п}                                       Д.'ТГ to

J J| f ( e , Ф )|²sin e d e d ф = — у Im A 1 °..     (19)

0 0                                   ^k 1 = 0

Стоящий в (19) слева интеграл равен полному поперечному сечению рассеяния включения Q [17]. Имеет место следующая оптическая теорема [17, с. 69], справедливая в том числе и в системах с потерями [18, с. 241]:

2 ππ

Q = J Jl f (e,ф )I 2 sin ededф = -pIm( f (e = o)). 00                    k

Учитывая в (4), что P (1) = 1 и P m (1) = 0 при m = 1,2,..., получаем для Q

Здесь E st = —— — средняя плотность энергии в ρc ²

стоячей волне.

Таким образом, получены формулы для перекрестной составляющей сил радиационного давления для бегущей (выражение (16)) и стоячей (выражение (17)) плоских волн, выраженные через зональные коэффициенты разложения соответствующих амплитуд рассеяния в ряд (4) по сферическим функциям. Для квадратичных составляющих в обоих случаях справедлива формула (14).

Отметим, что в каждом рассматриваемом случае первичного поля фигурирующие в (14) и (16) для бегущей волны и в (14) и (17) для стоячей волны следует различать амплитуды рассеяния f (θ,ϕ) из (13), т. к. поле рассеяния зависит от первичного поля.

Детализируем полученные выражения

Случай плоской бегущей волны

В работе [9] предложено выражение для суммарного радиационного давления, справедливое только в случае падающей плоской бегущей волны. В случае падающей волны вида p i _nc ( x ) = p ₀ e ik

^{2 п п}                                Атт to

Q = J J| ^f >^{( e} , Ф fsin ^{e d e d} Ф = -rS^Im( A ⁰⁾ 0 0                                   k l = 0

и, следовательно, подтверждаем справедливость равенства (19).

Как видно, выражение в (16) просто аннулируется при Im( A₁ ⁰ ) = 0, 1 = 0,1,2,... Можно показать, по крайней мере для сферически симметричных жидких включений без потерь аналогично тому, как это проделано в работе [19, с. 224], что справедливо следующее равенство

2 i δ l

A ⁰ = (2 1 + 1) e ------, 1 = 0,1,2,...

^l                     2 ik ,          ^{, , ,}

Здесь δ_l — действительные числа. Отсюда очевидно, что в общем случае Im( A₁ ⁰ ) ^ 0.

Из (16) видно, что если по каким-либо соображениям оставлять в коэффициентах Al0 только реальные составляющие (т. е. по умолчанию полагать Im(A,0) ^ 0), то выражение (16) будет тождественно равно нулю при любых Re(Al0 ) . Вызвано это тем, что в случае плоской волны слагаемые, соответствующие Re(A,0), I = 0,1,2,..., обнуляют само подынтегральное выражение в (2). Ровно это и произошло в работе [9], из чего и было сделано заключение о непригодности (2) в случае плоской бегущей волны.

Остановимся на анализе квадратичной составляющей (14) в случае бегущей волны. Как видно из сравнения (4а) с (14), компоненты силы F i ) квадратичной составляющей равны с точностью до постоянных множителей коэффициентам A ₁ ⁰ ( i = 3 ), A ,¹ ( i = 1), и B 1¹ ( i = 2) из разложения (4) для функции f ( θ , ϕ ) ² . Следовательно, в общем случае f ( θ , ϕ ) x и y компоненты квадратичной составляющей силы не равны нулю в отличие от перекрестной составляющей. Очевидно, что последние рассуждения в полной мере касаются и случая стоячей первичной волны.

Наконец, в случае азимутальной симметрии амплитуды рассеяния f (9, ф ) = f (9 ) с коэффициентами в разложении (4)      A , ⁰ = A , ,

( A m = 0, B^m = 0, m = 1,2,...) для случая плоской бегущей волны прямыми вычислениями легко получить формулу

F_z (“) = - 4пЕ У ^{2( 1 +} 1) Ref A(A_UX Й.    (20)

= 4 1 ² + 8 / + 3 ^{( 1 ( 1+1} ) )

Остальные компоненты в силу симметрии равны нулю. Таким образом, полная сила в этом случае равна сумме выражений (16) и (20) и направлена вдоль распространения волны

—  4 —

Fz = — Е х

k xfy Im A - k У 2(/ + 1) Ref A0 (A1+,)ll 1=        = 412 + 81 + 3   ( M/   )J   (21)

Случай плоской стоячей волны

Детализируем общие выражения (14) и (17) для сил в стоячей волне для случая конгломерата сферических частиц, образующих единое целое, например, в процессе агглютинации. Пусть амплитуда рассеяния отдельной сферической частицы в поле e^ikz имеет азимутально-симметричный характер f ₀ ( θ ) . Выражение для f ₀ ( θ ) имеет вид [20]

(2/ + 1)

чения; A_t =------ a • Пусть далее f ( 9 , ф ) — диа- ^l       2 ik     ^{l                          1}

грамма направленности дискретной апертуры, совпадающей с центрами сцепленных частиц. Тогда при условии малости вклада многократного рассеяния для конгломерата частиц его амплитуда рассеяния в поле eikz равна f0(θ) f1(θ,ϕ) . Очевидно, что в поле стоячей волны Pnc = P0 (eik(z+h) + e-ik(z+h)) = 2P0 cos к(z + h) амплитуда рассеяния конгломерата, фигурирующая в (13), равна f (9,ф) = (e f, (9) + e-ikhf, (n -9))fX9,Ф). (23)

Упростим выражение (17) в частном случае, когда функция f ₁ ( θ , ϕ ) удовлетворяет свойству

f (9,ф)= f (п - 9, Ф)

(плоскость z= 0 является плоскостью симметрии). Из (22), учитывая свойство полиномов Лежандра р (cos 9) = (-1)P (cos(n - 9)), имеем to f, (п - 9 ) = = (-1) /A/P/(cos9).         (22а)

I = 0

Введем обозначения      f+ (9) = f, (9), f - (9) = f) (n - 9). Тогда (23) перепишется в виде f (9, ф) = (eikhf+ (9) + e-ikhf - (9)) f (9,ф). (23а)

Введем обозначения F ± ( 9 , ф ) = f ± ( 9 ) f 1 ( 9 , ф ). Тогда суммарная амплитуда рассеяния равна f ( 9 , ф ) = e ikh F ⁺ ( 9 , ф ) + e - ^ikhF - ( 9 , ф ). Учитывая свойства функций f ± ( 9 ) , и f1 (9,ф ), имеем f -( 9 ) f 1 ( 9 , ф ) = f ⁺ ( п - 9 ) f 1 (п - 9 , ф ). Тогда из (4) получаем тождество A , ^{0 -}= ( - 1) ^/A_/ ^{0 +} , I = 0,1,2, где A , ⁰ ± коэффициенты разложения вида (4) функций F ± (9,ф ). А учитывая (23а), получаем, что коэффициенты A_l ⁰ для функции f ( θ , ϕ ) из (4) равны

A , ⁰ = At ⁰⁺

2cos kh , I -

2i sin kh, I - четное, нечетное.

Окончательно (17) сводится к виду

”

f > ( 9 ) = mF I ^a / (2 / + 1) Pl (cos 9 ) =

2 ik 1=5

- ( is )    - 4nE st .

F z =------- sin 2 kh x k

to

= I AP ^(cos9 )•

I = 0

to x=Re (A/ o+)J

I = 0

f [* /2 ]

I ( - 1)

n = 0

I - n

(2 / - 2 n )!

2 ^/n !( / - n )!( / - 2 n )

Здесь α_l — постоянные коэффициенты, зависящие от частоты и параметров сферического вклю-

Выражение в фигурных скобках в последнем выражении сворачивается вследствие свойства

Pt (1) = 1:

тальной симметрией:

f (0 ) = A + A 1 cos0 .            (27)

^[ i - n        ^{(2 l} - ^{2 n )!}        = ( - 1) i .

n = 0         2 l n !( l - n )!( l - 2 n )!

Окончательно получаем

F z(-s) = 4 ^{n Es} t sin2 kh ^( - I) l Re ( a ₀ + ) . (24) k          t0        ^{x 7}

Напомним, что A l ^{0 +} — зональные коэффициенты в разложении (4) функции F ⁺ ( 0 , ф ) = = f ⁺ ( 0 ) f₁ (0,ф ). Последнее выражение уже имеет классический вид, как для одиночной мелкой частицы [6, 8, 9].

Выражение (24) максимально упрощается в случае одиночного сферического включения с амплитудой рассеяния (22) с коэффициентами разложения A l , т. е. в случае f (0, ф ) ^ 1:

F z () = ^{4 n Es} t sin 2 kh ^( - 1) l Re ( A ) .    (25)

k        t0

Прямым вычислением (14) получаем для квадратичной составляющей

( ss )

Fz   = -4nEst sin 2kh x xy 2(l + 1) (-1)l I/A (A t0412 + 81 + 3           ( l ( l+1) ),

F ,⁽ss ) = 0, i = 1,2.

Окончательное выражение для полной силы в этом случае таково

Пусть c ₁ и ρ ₁ — скорость и плотность шарика соответственно, n = c / c 1 — показатель преломления, в = P i / P — отношение плотности включения к плотности пространства, k 1 = о / с 1 . Пользуясь техникой, изложенной в [19, задача 82], получаем после несложных вычислений для A_l , l = 0,1:

Re( A o ) =

^Im( A o ) =

Re( A 1 ) =

^Im( A 1 ) =

^{( n 2} - ^в ) ^k ’ ^{a 3} + O ( k'a ’), 3 β

( n ² - в ) ² k ⁵ a ⁶        _{7 8}

+ O ( k ⁷ a ⁸ );

9 β ²

^{( в} - 1) k ^{2 a} 3 + O ( k ⁴ a ⁵ ), (2 в + 1)

( в - 1) ² k ⁵ a ⁶        _{7 8}

—— ----+ O ( k ⁷ a ⁸ ).

3(2 в + 1) ²

Получи м из (18) продольное радиационное давление F z для включения с ампл ит удой рассеяния (27), (28) по старой методике F_z ^' с помощью прямых вычислений, где учитываются только реальные составляющие, и с учетом полученных выше соотно ше ний (21), где вычисления производятся точно F_z ^'' . Окончательно имеем:

4 π

F = —E x z 3

x ( 3Re( A_o ⁰ ) ² + Re( A 1⁰ ) ² - 2Re( A_o ⁰ )Re( A 1⁰ ) ) ,   (29)

Fz =-Est 4n sin 2kh x xJ 1 j (-1)l Re (Al) +

I k l = 0

+f 2⁽ l ⁺ 1) ( - 1) l M A ( Au i ) * )l           (26)

£0 4 1 ² + 8 1 + 3          \ ^{lV l +U} /J

Отметим, что частные выражения для сферических включений (21) и (26) совпадают с полученными в работах [12, 13], представленными, правда, в других обозначениях.

В качестве примера расчетов по полученным выражениям перепроверим классический случай силы радиационного давления на жидкий шарик в поле плоской бегущей волны при условии малости его волновых размеров ka <<  1, где a — радиус шарика. При этих условиях в амплитуде рассеяния необходимо удерживать только монопольный и дипольный моменты, а сама она обладает азиму-

F z = 4nE x

( Im( A ⁰) Im( A ⁰) 2          /лоч)

x I     k ⁺ k " jRe( A ¹⁰ )Re( A 1⁰ ) I .

Сам результат в (29), (30) имеет порядок O ( k ⁴ a ⁶ ) , что следует из (28). Анализ (29), (30) с учетом (28) показывае т, чт о в рассматриваемом примере разность F z - F z имеет порядок F z' - F z' = O ( k ⁸ a ¹⁰ ) и оба результата F z и F z практически тождественны. Это объясняется малостью мнимых составляющих по сравнению с действительными составляющими в данном рассматриваемом случае (28). В общем случае необходимо пользоваться точны м и выражениями (21). Отметим кроме того, что F _z ^' из (29) совпадает с результатами, полученными в [8, 9 и др.].

Подтвердим подмеченный в [10] факт того, что если для включения (27) выполняется одно из равенств A 0 = 0 или A 1 = 0, то квадратичная составляющая радиационного давления равна нулю. Это следует непосредственно из (20).

Далее остановимся на случае стоячей плоской волны. Как следует из выражения (23) для включений с амплитудой рассеяния вида f (0,ф ) = = f (п - 0, ф ), выражение (2) аннулирует все слагаемые, содержащие Im( A_l ⁰ ) , оставляя только слагаемые, содержащие Re( A_l ⁰ ) . Отсюда следует, что перекрестная составляющая радиационного давления на такое включение в поле стоячей плоской волны должна отличаться от аналогичного в бегущей волне пропорционально различиям между реальными Re( A_l ⁰ ) и мнимыми составляющими Im( A_l ⁰ ) . Из (28) сразу следует классический результат: для включения (27) соотношение между силами имеет порядок O (( ka ) ³ ) . Отметим, что это соотношение в работе [10] также из свойств включения было получено иначе.

ВЫВОДЫ

Таким образом, в рамках линейной теории рассеяния получены общие выражения, связывающие продольные и поперечные составляющие сил радиационного давления с амплитудой рассеяния произвольных включений в поле плоской бегущей и стоячей волн. Произведена детализация полученных выражений для различных частных случаев амплитуды рассеяния включения. Эти выражения включают полученные ранее формулы как частный случай.