Радиационные риски заболеваемости раком щитовидной железы, обусловленным облучением ликвидаторов радиоизотопами йода

Известно, что рак щитовидной железы относится к локализациям, имеющим максимальные радиационные риски [12]. Особый научный интерес к этой проблеме появился после аварии на ЧАЭС, когда в начале 90-х годов ХХ века был зарегистрирован существенный рост рака данной локализации среди детей, проживавших на загрязненных радионуклидами территориях [3, 6, 9-11]. Исследована заболеваемость раком щитовидной железы от дозы облучения от изотопов йода и среди взрослого населения [5], у которых за рассматриваемый период наблюдения радиационных рисков не выявлено.

Проблема заболеваемости раком щитовидной железы среди ликвидаторов последствий аварии на ЧАЭС также представлена в публикациях [4, 7, 8]. В работах [7, 8] для оценки риска использовалось сравнение заболеваемости до и после аварии на ЧАЭС и получены значимые значения риска. В работе [4] использован регрессионный анализ заболеваемости от дозы внешнего облучения, который не выявил радиационных рисков. Как следует из этих публикаций, проблема заболеваемости раком щитовидной железы до настоящего времени не решена.

Иванов В . К . – Первый зам . Председателя РНКРЗ , зам . директора по научной работе , член - корреспондент РАМН ; Горский А . И.* – веду щий научный сотрудник , к . т . н .; Максютов М . А . – зав . лабораторией , к . т . н .; Туманов К . А . – научный сотрудник ; Кащеев В . В . – аспирант . МРНЦ РАМН .

Возможной причиной таких противоречивых результатов является отсутствие документированных доз на щитовидную железу от радиоизотопов йода. В данной работе представлена оценка радиационных рисков рака щитовидной железы с использованием физических свойств кривой распада 131I и введением суррогатных доз. Отметим, что такие подходы достаточно широко применяются в эпидемиологической практике.

Материалы и методы

Методы анализа

Облученные versus необлученные . Основная трудность анализа заболеваемости раком щитовидной железы среди ликвидаторов, обусловленным радиоизотопами йода, заключается в том, что дозы у ликвидаторов в щитовидной железе практически неизвестны. Воспользуемся для анализа свойствами облучения ликвидаторов этим изотопом. Известно, что период полураспада ¹³¹I равен 8 суткам (постоянная распада λ =0,087) и динамика распада описывается

N(t) уравнением:

N 0

t

∫ exp( - λ ⋅ τ)dτ , где N 0 – начальная концентрация изотопа.

На рисунке 1 приведена кривая уменьшения относительной концентрации этого изотопа

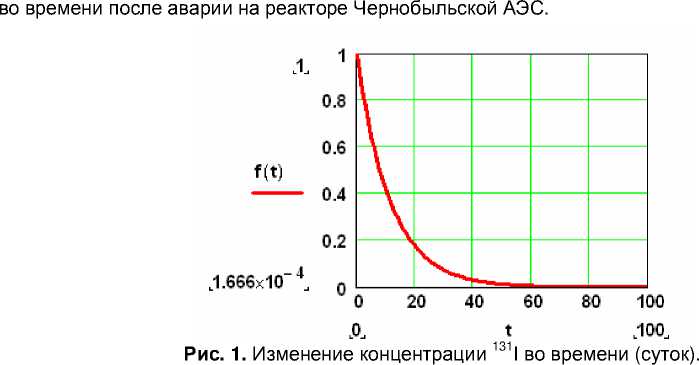
Из рисунка 1 видно, что концентрация этого изотопа практически исчезает через два месяца после его появления.

Будем считать, что источник радиоактивного йода распределен равномерно по зоне облучения. Известно, что было несколько выбросов радионуклидов до 9 мая 1986 г. Для упрощения положим, что весь йод был выброшен в момент аварии 26 апреля 1986 г. и его распад во времени подчиняется распределению, приведенному на рисунке 1.

Разделим всю когорту на две подкогорты: ликвидаторы, которые работали в зоне до июля 1986 г. (65 дней после аварии), в этот момент концентрация йода практически равна нулю, и все остальные. Будем считать, что первая когорта подверглась йодному облучению (облучен- ная когорта), а вторая - нет (необлученная когорта). Так как при таком моделировании отсутствует понятие доза, в анализе использована информация обо всех ликвидаторах, в том числе (и не имеющих документированные дозы) и случаях заболеваний, что является его преимуществом.

Самым простым подходом в рамках выбранной модели облучения является анализ эффекта облучения, который заключается в сравнении числа событий в двух группах: облученных ( к =2, к - индекс группы) versus необлученных ( к =1), методология анализа описана в [1]. Под облучением здесь понимается воздействие ионизирующего излучения или других токсикогенных факторов.

Предположим, что O 1 и O 2 (число событий в группах) - пуассоновские переменные соответственно со средними 6 1 ■ E 1 и 6 2 ■ E 2 . Применение пуассоновского распределения вполне оправдано, так как заболевания раком щитовидной железы являются редкими событиями. Здесь E 1 и E 2 представляют ожидаемые числа событий в группах, а 6 представляет стандартизованное число событий в группах по отношению к стандартизованному числу событий, например, в референтной (контрольной) группе. Тогда отношение 6 2 / 6 1 представляет относительный риск во второй группе при использовании первой группы как референтной.

Если предположить, что 6 = 61, у = у2 = 62 /61 и 6 ■ у = 62, то интересующим нас параметром является относительный риск у (отношения частот событий в сравниваемых груп пах), а параметр 6 играет роль несущественного параметра. Согласно классическим принци- пам статистики, при таких обстоятельствах удобно рассматривать распределение наблюдаемых данных как зависящих только от интересующего параметра [1].

Для получения статистического критерия используется тот факт, что условное распределение двух пуассоновских переменных на их сумму является биномиальным распределением [1].

Плотность этого распределения можно выразить формулой:

pr(O2|O+ ;у) = (°+ ) ■ по2 ■ (1 - яр1, о2

где O + = O i + O 2 ,

П = ly’Ehr, E1 + у ■ E2

или эквивалентно:

п ■ E-.

ψ=      1

.

(1 - П ■ E2

Точный односторонний критерий для проверки нулевой гипотезы у о = 1 (отсутствие эффекта облучения), получаемый из «хвоста» биномиального распределения, имеет вид:

O+ о,

- x

.

P - £ (   ) ■ п0 ■ (1 - п0 ) +

• x - O 2 ^x

В рамках нулевой гипотезы п ₀ - E 2 ■ Первый сомножитель в скобках под знаком суммы ^и   E +

• - число сочетаний из O ₊ по x . На практике обычно пользуются приближенной хи-квадрат статистикой, основанной на разности наблюдаемого числа событий от ожидаемого. В этом случае можно записать двусторонний критерий для проверки нулевой гипотезы [1] – отсутствие эффекта облучения:

(O2 - E;| - 0,5)2   ((O2 - E21- 0,5)2 )

X ² - ^J----- 4------ +----- 4------ ,                    (5)

^E 2                  ^E 1

где E*k - O+ ■ (Ek/E+ ), E+ - E1 + E2 из условия, что £kE*k - £ROk .

Числитель в выражении (5) уменьшен на величину 0,5 для коррекции на непрерывность при асимптотическом переходе к нормальному распределению.

Наличие двух сравниваемых групп дает возможность сделать точечную оценку величины относительного риска. Оценка максимального правдоподобия для относительного риска в рамках модели (4) имеет вид [1]:

V -

O 2 ■ E 1 0 1 ■ E 2 .

Оценка точных 100-(1-a % доверительных интервалов для п производится по формулам [1]:

______________O 2______________

O2 + (01 +1) ■ Ра/2 (2 ■ O1 + 2,2 ■ O2) ’_ - (O2 +1) ■ Ра/2 (2 ■ O2 + 2,2 ■ O1)U O1 + (O2 +1) ■ Fa/2 (2 ■ O2 + 2,2 ■ O1) ’ где Fa/2(v1 ,u2) - обозначает верхний 100a/2 персентиль распределения Фишера с и1 и и2 степенями свободы. Доверительные интервалы для у определяются подстановкой значений, полученных из (7, 8), в уравнение (3).

Чтобы применить изложенную методику, необходимо определить величины Е 1 и Е 2 . Для определения ожидаемого числа случаев можно использовать возрастные национальные показатели заболеваемости и число человеко-лет в рассматриваемых когортах в соответствующих возрастных группах (внешний контроль). Их произведение будет равно ожидаемым случаям. Однако использование внешнего контроля может привести к смещению оценок риска, обусловленных разной выявляемостью заболеваний (ликвидаторы проходят регулярные специализированные осмотры) в когорте ликвидаторов и по данным официальной медицинской статистики. Поэтому для анализа воспользуемся данными исключительно о самой когорте (внутренней стандартизацией).

Методология точечных оценок риска по такой технологии (внутренней стандартизации) описана в [1]. Следует отметить, что и этот подход не лишен недостатков из-за возможного влияния смешивающих факторов, таких как возраст, время и других стратификационных переменных. Тем не менее, этот подход представляется полезным вследствие его относительной простоты и интуитивной очевидности. Расчеты, необходимые для внутренней стандартизации, достаточно просты. Для обобщения предположим, что данные разбиты на J категорий по возрасту и K категорий по уровню облучения.

Представим наши данные в виде таблицы 1.

Таблица 1 Структура таблицы стратификационных данных

Страта ( j )	Параметр	1	2	............	K	Всего
1	Случаи	d 1,1	d 1,2	............	d 1,K	D 1
	Чел.-годы	py 1,1	py 1,2	............	py 1,K	PY 1
2	Случаи	d 2,1	d 1,2	............	d 2,K	D 2
	Чел.-годы	py 2,1	py 1,2	............	py 2,K	PY 2
. . .	. . .	. . .	. . .	............	. . .	. . .
J	Случаи	d J,1	d J,2		d J,K	D J
	Чел.-годы	py J,1	py J,2		py J,K	PY J
Всего	Случаи	O 1	O 2		O K	O +
	Чел.-годы	py +1	py +2		py +K	PY + =py ++

Тогда ожидаемое число случаев для k -го уровня облучения определится из выражения (9), в предположении, что эффект облучения не влияет на интенсивность заболеваний:

JD

E k = I py j,k ■ ^j .                                          (9)

j = 1        ^PYj

Величины Е k нормированы так, что их сумма равна наблюдаемому числу случаев.

Подход с двумя дозовыми группами (облученные versus необлученные) может оказаться приближенным, если сравниваемые группы имеют разные возрастные распределения, так как заболеваемость зависит не только от дозы, но и от возраста, который является смешивающим фактором (confounding factor) [1]. Поэтому более точным является подход со стратификацией данных по смешивающему фактору (в данном случае возрасту). Произведем группировку данных по возрасту на I страт, оставаясь в рамках двухгрупповой (облученные ( K =2) versus необ-лученные ( K =1)) модели.

Представим стратифицированные данные в виде серии таблиц 2х2 (таблица 2).

Таблица 2

Иллюстрация таблицы 2 х 2

	Облученные	Необлученные
Случаи	a i	b i	n 1i
Когорта	c i	d i	n 0i
	m 1i	m 0i	N i

В практике эпидемиологии онкологических заболеваний для определения относительного риска для таких стратифицированных данных широко используется подход, имеющий название оценка «Mantel-Haenszel» (MH) [1], который достаточно прост, но позволяет давать устойчивые оценки, альтернативные и близкие к оценкам максимального правдоподобия.

Оценка относительного риска в рамках этого подхода имеет вид:

I

2 a i ■ d i /N i

уmh = iT^           ■                                                          (10)

2 bi- Ci/Ni i=1

Надчеркивание над У означает оценку риска. Фактически это взвешенное среднее относительных рисков в стратах с весами, которые представляют приближенную обратную дисперсию отдельных оценок.

Приближенные доверительные интервалы оцениваются из решения следующих уравнений.

Нижний:

I ∑ a i i = 1

I

- 0,5 - 2 vl ■ i=1

(a i ⁺ b i ) ' c i (d i + Vl • C i )

I

= Z a / 2 "  ⁽ 2 ^VL "  i = 1

(a i ⁺ b i ) ' c i ' d i ) 0 , 5 (d i + V L C i ) ²       .

Верхний:

II

2 a i ^{+ 0 , 5 -} 2 ^y U "  i = 1                i = 1

(ai + bi)' ci _ 7               (ai + bi)" ci " di )0, 5

= ^- Z a/ 2 "  I 2 ^y U              "2"" )

^(di ^{+ y} U "  c i )             i = 1       (d i + V u C i )

где Z _{a /} 2 100(1- a ) - персентиль стандартного нормального распределения.

Тест значимости на проверку нулевой гипотезы *f=1 имеет вид:

(

Л 1 =

II

2 (ai+ b) - 2

i = 1                  i = 1

c i " d i " (a i ⁺ b i ) c i ⁺ d i

- 0, 5 ))

у ci • di • (ai + bi )

² (C i + d i ))

Для контроля точности оценки относительного риска в рамках модели MH можно вос- пользоваться оценкой максимального правдоподобия (MLE), решив уравнение:

II

2 (a i + b) = 2

i = 1                   i = 1

(a i + b i ) ■ C i ■ у d i + V ■ C i )

Основным предположением в рамках двухгрупповой модели облучения, лежащим в основе оценки для общего относительного риска по модели MH и других подходов со стратификацией данных, является равенство относительного риска во всех используемых стратах (возраст, календарное время, пол и т.д.).

Для проверки этого предположения разработан специальный тест (тест на гетерогенность относительного риска – эффект модифицирующих факторов) [1].

)

) ψ ⋅ c                  )             )

Положим π = ⁱ , обозначим c = (a + b ) ⋅ π – ожидаемое число заболе- ⁱ (d i + ψ ⋅ c i )                       ^{i i i i}

)

ваний среди облученных, для необлученных – d_i = (a_i + b_i) ⋅ ( 1 - π ⁾ _i ) .

Тогда тест на гетерогенность имеет вид:

2         (di - di)    (ci -ci)

χI-1 = ∑ (    )     +    )

i = 1         ^di                ^ci

Тест на тренд относительного риска по возрасту выразится уравнением:

2 ^χ 1 ⁼

I

(∑i⋅(ci - c)i))2

i = 1

I ∑ i ² i = 1

)

⋅ ci ⋅ di /(ai + bi)-

I )

(∑i⋅c)i ⋅di/(ai + bi))2

i = 1

)

(ci ⋅ di /( ai + bi ))

Если число облученных групп более двух ( к =2,..., K ), применяется аналогичный подход, только в этом случае оценка MH рассчитывается для каждого уровня облучения относительно контрольного. Для теста значимости эффекта облучения для каждого уровня облучения используется статистика (13).

Для глобального теста, проверяющего равенство наблюдаемых и ожидаемых чисел событий группированных (стратифицированных) данных, используется критерий [1]:

χk2=(O-E)T⋅V-⋅(O-E),

где (обозначения приведены в таблице 1) O = (O 1 , O 2 ,…, O K ) и E = (E 1 , E 2 ,…, E K ) – векторы наблюдаемых и ожидаемых чисел событий в K -дозовых группах, T – знак транспонирования,

• V ^- – обратная ковариационная матрица V = ∑ V_i . На практике она заменяется обратной

(K- 1 ) × (K- 1 ) ковариационной матрицей.

Ожидаемое число событий в k -й дозовой группе рассчитывается по формуле (9).

Элементы ковариационной матрицы ( k , l ) определяются из выражения:

• V i    _k,l = py i,k ⋅ (PY i - py i,k ) ⋅ _P ^D _Y ⁱ _{i 2} , если k = l ;

  V_{i k,l} = - py_i,k ⋅ py_i,l ⋅ _PY ⁱ _{i 2} ,

  
  

  если k ≠ l .

  
  
  
  

Тест для тренда относительного риска по дозе облучения записывается в виде [1]:

χ1 =

K

где ei,k =

K

( ∑xk ⋅ (Ok - Ek))2 k=1

∑xk2⋅Ek-∑ k=1

k = 1

pyi,k ⋅ Di PYi