Радиальные распределения величины магнитного поля в солнечной короне, полученные с использованием сведений о быстрых ГАЛО-КВМ
Автор: Файнштейн В.Г., Егоров Я.И.
Журнал: Солнечно-земная физика @solnechno-zemnaya-fizika
Статья в выпуске: 1 т.4, 2018 года.
Бесплатный доступ
В последние годы для измерения магнитного поля в солнечной короне используют сведения о расстоянии между телом быстрого коронального выброса массы (КВМ) и связанной с ним ударной волны. Во всех случаях этот подход применялся для нахождения радиальных распределений поля B(R) для направлений, почти перпендикулярных лучу зрения. Мы модифицировали этот метод для получения распределений B(R) поля вдоль направлений, близких к оси Солнце-Земля. Для этого с использованием модели ice-cream cone для КВМ по данным коронографов LASCO находились трехмерные характеристики быстрых КВМ типа гало и связанных с ними ударных волн, движущихся почти вдоль оси Солнце-Земля. С помощью этих данных удалось получить распределения B(R) QUOTE до расстояния от центра Солнца ≈43 радиуса Солнца, что примерно в два раза дальше, чем в предыдущих работах, в которых использовались данные LASCO. Полученные результаты оказались в хорошем согласии с результатами предшествующих работ для расстояний до 20 радиусов Солнца. Сделан вывод о том, что для повышения точности такого метода нахождения поля в короне необходимо разработать способ выделения участков КВМ, движущихся в медленном и в быстром солнечном ветре. Предложен способ отбора КВМ, центральная (приосевая) часть которых действительно движется в медленном ветре.
Квм, ударные волны, солнечный ветер, магнитное поле
Короткий адрес: https://sciup.org/142220274
IDR: 142220274 | УДК: 523-98 | DOI: 10.12737/szf-41201801
Текст научной статьи Радиальные распределения величины магнитного поля в солнечной короне, полученные с использованием сведений о быстрых ГАЛО-КВМ
Корональная плазма погружена в неоднородное и анизотропное магнитное поле. Структура короны, а также протекающие в ней взрывные, эруптивные процессы тесно связаны с характеристиками магнитного поля на различных пространственных масштабах. В связи с этим разработка надежных и точных методов определения магнитного поля в солнечной короне — одна из ключевых задач, стоящих перед исследователями Солнца.
Регулярные измерения магнитного поля в солнечной короне не ведутся; проводились лишь от- дельные измерения, опирающиеся на эффекты Зеемана (в инфракрасном диапазоне) [Lin et al., 2000], Ханле [Sahal-Brechot et al., 1986], Фарадея [Pätzold et al., 1987; Spangler, 2005], а также на измерения солнечного радиоизлучения [Lee, 2007; Bogod, Yasnov, 2016]. Магнитное поле в короне может быть восстановлено в рамках различных приближений, опираясь на измерения фотосферного поля: в потенциальном приближении (см. [Rudenko, 2001] и цитируемую там литературу), в бессиловом приближении [Wiegelmann, 2008; Rudenko, Myshyakov, 2009]. Отдельные оценки магнитного поля в короне были
Таблица 1
|
Дата, д.м.г. |
Время |
Скорость, км/с |
Координаты вспышки |
Класс вспышки |
|
18.11.03 |
8:50:05 |
1660 |
N00E18 |
M3.9 |
|
06.04.04 |
13:31:43 |
1368 |
S18E15 |
M2.4 |
|
03.11.04 |
16:54:05 |
1759 |
N09W17 |
X2.0 |
|
07.11.04 |
16:54:05 |
1759 |
N09W17 |
X2.0 |
|
15.01.05 |
23:06:50 |
2861 |
N15W05 |
X2.6 |
|
17.01.05 |
9:30:05 |
2094 |
N13W19 |
X2.2 |
|
30.07.05 |
6:50:28 |
1968 |
N12E60 |
X1.3 |
|
05.09.05 |
19:48:05 |
2257 |
источник за лимбом |
– |
|
13.09.05 |
20:00:05 |
1866 |
S09E10 |
X1.5. |
сделаны с учетом связи поля с различными характеристиками корональной плазмы, которые находились независимо, например параметр β, гирочастота, альфвеновская скорость (см. монографию [Schwenn, Marsch, 1990] и цитируемую там литературу).
В работах [Gopalswamy, Yashiro, 2011; Kim et al., 2012] предложен и протестирован новый метод нахождения значений магнитного поля в солнечной короне. Метод опирается на существование связи между нормированным расстоянием (normalized standoff distance в англоязычной литературе) от наиболее удаленной от Солнца части КВМ (от «носа» КВМ) до связанной с КВМ ударной волны (УВ) и альфвеновским числом Маха M [Russell, Mulligan, 2002], а как следствие, и альфвеновской скоростью. В работе [Kim et al., 2012] для нахождения M использовалась также связь числа Маха с величиной скачка плотности на фронте УВ [Ландау, Лифшиц, 1988]. Метод [Gopalswamy, Yashiro, 2011; Kim et al., 2012] был применен для нахождения радиальных распределений магнитного поля B(R) в плоскости неба на расстояниях примерно до 20RS (RS — радиус Солнца) по данным коронографов COR2, входящих в комплекс инструментов Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI) [Howard et al., 2008] на борту миссии Solar Terrestrial Relations Observatory (STEREO) [Kaiser et al., 2008], и телескопов С2 и С3 Large Angle and Spectrometric Coronagraph (LASCO) [Brueckner et al., 1995] на борту миссии Solar and Heliospheric Observatory (SOHO). Для нахождения B(R) в этом случае анализировались «лимбовые» КВМ, т. е. выбросы массы, источники которых находятся относительно близко к солнечному лимбу. Этот метод в работе [Poomvises et al., 2012] был применен для расстояний до ≈120 RS с использованием данных SOHO/LASCO и телескопов Heliospheric Imager 1, входящих в группу инструментов SECCHI. В работе [Schmidt et al., 2016] для КВМ, зарегистрированного 29 ноября 2013 г., были сопоставлены радиальные распределения магнитного поля, полученные с использованием метода [Gopalswamy, Yashiro, 2011] и магнитогидродинамических трехмерных расчетов движения модельного КВМ, связанного с ударной волной. Сделан вывод о хорошем согласии полученных двумя способами радиальных распределений магнитного поля на расстояниях (1.8–10)RS.
В настоящей работе метод нахождения величины магнитной индукции во внешней короне, предложенный [Gopalswamy, Yashiro, 2011] , применен для быстрых корональных выбросов массы типа гало (ГКВМ) с источниками большинства из них вблизи центра солнечного диска. Такие КВМ движутся под небольшим углом к оси Солнце—Земля [Fainshtein, 2006] . Поэтому для нахождения кинематических характеристик тела КВМ и УВ, необходимых для определения распределения магнитного поля вдоль направления движения таких КВМ, нужно проводить расчеты характеристик КВМ в трехмерном пространстве. Для нахождения положения и скорости границы тела ГКВМ и связанной с ним УВ в трехмерном пространстве мы использовали ice-cream cone model, рассмотренную в работе [Xue et al., 2005] . Полученные с использованием характеристик ГКВМ радиальные распределения магнитного поля были сопоставлены с распределениями поля по данным наблюдений лимбовых КВМ из работы [Kim et al., 2012] . И, наконец, в работе обсуждается проблема установления типа (быстрый или медленный) солнечного ветра (СВ), в пределах которого движется та или иная часть тела КВМ. В качестве первого шага решения этой проблемы в работе предлагается способ отбора КВМ, центральная часть которых двигается в медленном СВ.
ДАННЫЕ И МЕТОДЫ ИССЛЕДОВАНИЯ
Выбранные для анализа быстрые ГКВМ приведены в табл. 1. Для каждого события указаны дата и время первой регистрации ГКВМ в поле зрения коронографа LASCO C2, линейная проекционная скорость КВМ, координаты и рентгеновский балл связанной с ГКВМ вспышки из каталога [].
Для нахождения трехмерных (3D) параметров ГКВМ (положение оси ГКВМ в пространстве, или, что то же самое, направление движения выброса массы, угловой размер ГКВМ 2αCME, положение r p и скорость v p внешней границы ГКВМ на оси модели в зависимости от времени) мы использовали метод, предложенный в работе [Xue et al., 2005] , в которой
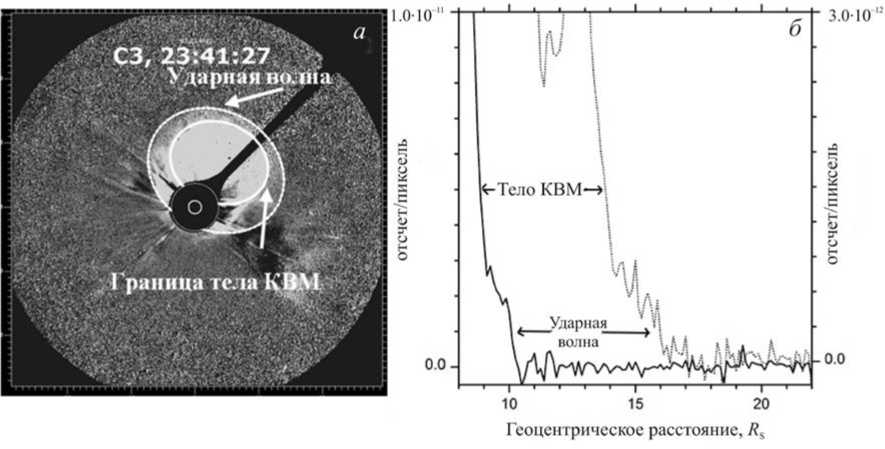
Рис. 1 . Панель а — ГКВМ, зарегистрированный 15.01.2005 в 23:41:27. Белыми эллипсами показаны границы тела выброса массы (яркая внутренняя область) и ударной волны (граница внешней диффузной области). Панель б — распределения яркости вдоль направления на западном лимбе под углом к экватору 30° северной широты для двух моментов времени ( t 1=23:17:25 и t 2=23:41:27). Отчетливо выделяются скачки яркости, указанные стрелками от слов «ударная волна», с пространственным размером (1–2)δ R , где δ R ≈0.125 R S — пространственное разрешение коронографа LASCO C3. Предполагается, что это бесстолкновительная ударная волна. Данные на левой вертикальной оси на панели б относятся к левой кривой, данные на правой вертикальной оси — к правой кривой
в качестве модели выброса массы использовалась так называемая ice-cream cone model. В этой модели КВМ представляется в виде конуса с вершиной в центре Солнца, опирающегося на часть сферической поверхности с радиусом, равным длине образующей конуса. Направление движения ГКВМ определяется положением в пространстве оси модельного конуса, которое описывается двумя углами: θ 0 и φ 0 . Угол θ 0 (коширота, θ 0=[0°–180°]) отсчитывается по часовой стрелке от положительного направления оси, проходящей через центр Солнца и перпендикулярной плоскости эклиптики (или плоскости солнечного экватора). Как и в работе [Xue et al., 2005] , мы пренебрегали различием между плоскостью эклиптики и плоскостью солнечного экватора. Долготный угол φ 0 отсчитывается в плоскости эклиптики от центрального меридиана против часовой стрелки: φ 0 =[0°–360°].
Отметим новые подходы, использованные нами для расчетов параметров ice-cream cone model. В отличие от работы [Xue et al., 2005] в настоящей работе: а) параметры модельного КВМ в трехмерном пространстве рассчитывались отдельно для тела КВМ и связанной с ним УВ; б) рассчитывались не только скорости указанных структур, но и их положения вдоль направления движения модельного КВМ в трехмерном пространстве в разные моменты времени; в) граница проекции тела реального КВМ и УВ на плоскость неба выделялась не только дискретным набором точек на этих структурах, но и путем аппроксимации этих структур эллипсами или участками эллипсов.
На первый взгляд, модель ice-cream cone — очень простая модель КВМ и для решения поставленной задачи стоило бы использовать более реалистичные модели КВМ. В работе [Michalek, 2006]
использовалась считающаяся более реалистичной коническая модель КВМ с эллиптической формой основания модельного конуса. В работе [Thernisien et al., 2006] использована еще более реалистичная модель КВМ в виде магнитоплазменного жгута. Одним из оснований использования для расчетов 3D-параметров КВМ и связанной с ним УВ конической модели, предложенной в [Xue et al., 2005] , являются результаты работы [Kim et al., 2011] , в которой показано, что радиальные скорости КВМ, рассчитанные с использованием моделей КВМ, предложенных [Michalek, 2006; Thernisien et al., 2006] , очень близки (коэффициент корреляции оказался более 0.95) к скоростям, рассчитанным с помощью метода [Xue et al., 2005] .
Наша реализация метода, предложенного в [Gopalswamy, Yashiro, 2011] , заключается в следующем:
-
1. Для каждого рассмотренного ГКВМ в различные моменты времени его движения в поле зрения коронографа LASCO C3 с использованием метода [Xue et al., 2005] рассчитывается расстояние между УВ и телом КВМ Δ R вдоль оси модельного выброса массы, а также радиус кривизны границы тела КВМ R C. Напомним, что, в отличие от работы [Xue et al., 2005] , где для расчетов 3D-параметров модельного КВМ использовались координаты дискретного набора точек на УВ в плоскости неба, в настоящей работе использовалась обводка как УВ, так и тела КВМ участками эллипсов (рис. 1).
-
2. Из соотношения [Russell, Mulligan, 2002]
-
3. Из формулы M= ( V sh –V SW)/ V A находится альфве-новская скорость V A. Здесь V sh — скорость ударной волны, V SW — скорость солнечного ветра, по которому распространяется УВ. Как и в работе [Gopalswamy, Yashiro, 2011] , мы полагали, что значительная часть КВМ движется в области медленного СВ, скорость которого находилась из соотношения [Sheeley et al., 1997]
-
4. Из формулы V A = 2.18·106 Bn –1/2 [Gopalswamy, Yashiro, 2011] находится магнитная индукция B (в Гс). Здесь n — концентрация частиц (в см–3) в коро-нальной плазме, которая приближенно полагалась равной концентрации электронов и находилась с помощью соотношения [Leblanc et al., 1998]
Δ R/R C = 0.81[(γ–1) M 2 + 2]/[(γ + 1) (M 2 – 1)]
находится альфвеновское число Маха М (считалось, как и в работе [Kim et al., 2012] , с результатами которой мы сравнили полученные результаты, что показатель адиабаты γ=4/3).
( V SW )2 = 1.75·105(1–exp(–( R –4.5)/15.2)).
n ( R ) = 3.3·105 R –2+4.1·106 R –4+8.0·107 R– 6, где R — расстояние из центра Солнца до точки наблюдения в радиусах Солнца.
РЕЗУЛЬТАТЫ
На рис. 1 показан ГКВМ в поле зрения коронографа LASCO C3 с обводками участками эллипса границы тела КВМ и УВ. Заметим, что обводка указанных структур не всегда производилась с их полным охватом по широте в пределах 360°. Мы обводили только те участки структур, которые могли надежно идентифицировать как тело ГКВМ или ударную волну. Анализ показал, что различие трехмерных параметров, рассчитанных для одних и тех же событий с неполной и полной (360°) обводками, относительно невелико.
Граница диффузной области впереди тела КВМ (или фронтальной структуры КВМ) считалась УВ, поскольку скорость этой границы относительно окружающего медленного СВ превышала альфве-новскую скорость (впервые эта идея сформулирована в работе [Sheeley et al., 2000]) и на отдельных участках этой границы на сканах яркости вдоль направлений, перпендикулярных границе, удается обнаружить скачки яркости с пространственным размером (1–2)δR (рис. 1, б), где δR≈0.125RS — пространственное разрешение коронографа LASCO C3. Такие УВ называют бесстолкновительными [Арцимович, Сагдеев, 1979], поскольку ширина их фронта во много раз меньше средней (приблизительно одинаковой) длины свободного пробега протонов и электронов при столкновениях с протонами в корональ-ной плазме LC (LC≈(1–3)RS в поле зрения коронографа LASCO C3). Реальная ширина фронта бесстолкновительной УВ, согласно [Арцимович, Сагдеев, 1979], с учетом характеристик корональной плазмы и магнитного поля во много раз меньше δR. В качестве примера оценим ширину фронта перпендикулярной (т. е. распространяющейся перпендикулярно магнитному полю) бесстолкновительной УВ. В этом случае ширина фронта УВ ∆ sh~ri, где ri — ларморовский радиус ионов. Оценку ∆sh проведем для расстояния R=23.82RS. На этом расстоянии, согласно нашим расчетам, B=6.39· 10–3 Гс. Оценку сделаем для преобладающего в корональной плазме типа ионов — протонов. Вполне разумной оценкой тем- пературы протонов Tр на выбранном расстоянии является значение Tр=5 · 105 К. Отсюда следует, что ∆sh~ri=1.02(Tр/11605)1/2/B=1.02(5·105/11605)1/2/ (6.39·10–3)≈1048 м << δR≈0.125RS≈87 000 000 м.
Для событий из табл. 1 результаты расчетов положения R / R S и скорости УВ V sh в 3D-пространстве в разные моменты времени, а также скорости медленного СВ V sw , альфвеновской скорости V A , параметра ∆ R / R C, альфвеновского числа Маха M и значения магнитного поля B (без указания событий, к которым каждое указанное значение параметра относится), приведены в табл. 2. Значения параметров из этой таблицы использовались для построения графиков на рис. 2–4.
На рис. 2 приведены результаты расчетов магнитного поля, полученные с использованием расчетов 3D-параметров ГКВМ. Из этого рисунка следует, что полученная зависимость B ( R ) (белые кружки) вполне удовлетворительно согласуется с ожидаемыми значениями магнитного поля в медленном СВ, показанными сплошной линией на рис. 2, а . Эта линия — график функции
B R = 11.1·10–5(215.5/( R / R S ))2 [Гс], где 11.1·10–5 — величина B R в горизонтальном, т. е. параллельном плоскости солнечного экватора, участке медленного СВ на орбите Земли, 215.5 — расстояние от Солнца до орбиты Земли в радиусах Солнца. Можно привести аргументы, что как в быстром, так и в медленном СВ радиальная компонента поля B R , начиная с R ≈3 R S , меняется обратно пропорционально квадрату расстояния (для межпланетного пространства (см. рис. 4.1 на с. 186 в работе [Schwenn, Marsch, 1990] ). Но для медленного СВ нужно сделать оговорку. При относительно больших расстояниях от Солнца, в том числе вблизи орбиты Земли, это справедливо только для горизонтальных, т. е. параллельных плоскости солнечного экватора, участков медленного СВ. Причина этого заключается в существовании взаимодействия быстрых и медленных потоков СВ в случае, если участок медленного СВ наклонен под относительно большим углом к плоскости солнечного экватора [Schwenn, Marsch, 1990; Fainshtein, 1991] . Это взаимодействие приводит к существенному изменению магнитного поля в области наклоненных участков медленного СВ по сравнению с его горизонтальными участками. Поэтому, если мы хотим оценить величину B R в короне, опираясь на значения этой компоненты поля на орбите Земли, нужно использовать значения B R на орбите Земли только в горизонтальных участках медленного СВ. Этот вопрос подробно обсуждается в работе [Fainshtein, 1991] , там же приводятся характерные значения магнитного поля и плотности протонов в некоторых горизонтальных участках медленного СВ на орбите Земли.
Нетрудно убедиться, что в диапазоне одних и тех же расстояний (9–15) R S, для которых проводились расчеты магнитного поля как в нашей работе, так и в работе [Kim et al., 2012] , различие результатов относительно невелико: полученное нами среднее за указанный период времени значение поля < B >=0.02 Гс, в работе [Kim et al., 2012] — < B >=0.019 и 0.015 Гс.
Таблица 2
|
R / R S |
V sh |
V SW |
V A |
∆ R / R C |
M |
B |
|
9.3 |
2121.6 |
217.9 |
1018 |
0.4 |
1.9 |
0.031 |
|
11.8 |
1646.9 |
258.4 |
1009.8 |
0.2 |
1.4 |
0.023 |
|
13.4 |
1956.5 |
278.4 |
569.2 |
0.3 |
2.9 |
0.011 |
|
13.8 |
2382.5 |
282.7 |
1528.3 |
1.1 |
1.4 |
0.03 |
|
14.1 |
2079.9 |
286.5 |
448.4 |
0.2 |
4 |
0.009 |
|
15.2 |
2997 |
297.1 |
1120.3 |
0.3 |
2.4 |
0.02 |
|
15.2 |
1573.1 |
297.3 |
873.8 |
0.2 |
1.5 |
0.016 |
|
16.4 |
1579.4 |
308.6 |
803.3 |
0.8 |
1.6 |
0.0131 |
|
16.5 |
1830.7 |
309 |
951.6 |
0.8 |
1.6 |
0.016 |
|
18.6 |
1992.6 |
325.1 |
620.8 |
0.2 |
2.7 |
0.009 |
|
21 |
2205 |
340.6 |
1399.7 |
1.2 |
1.3 |
0.0178 |
|
21.1 |
1534.7 |
340.9 |
735.1 |
0.7 |
1.6 |
0.009 |
|
21.5 |
2990.3 |
343 |
969.7 |
0.2 |
2.7 |
0.012 |
|
21.8 |
1604.4 |
345 |
858.5 |
0.8 |
1.5 |
0.011 |
|
23.3 |
1817.3 |
352.5 |
739.1 |
0.6 |
2 |
0.008 |
|
23.4 |
2135.9 |
352.8 |
934 |
0.4 |
1.9 |
0.011 |
|
23.8 |
2082.1 |
354.8 |
570.8 |
0.2 |
3 |
0.006 |
|
25.2 |
2554.8 |
360.7 |
963.2 |
0.6 |
2.3 |
0.01 |
|
28.2 |
2050.3 |
371.8 |
1277.4 |
1.2 |
1.3 |
0.012 |
|
29.7 |
1621.1 |
376.3 |
826.6 |
0.8 |
1.5 |
0.007 |
|
30.5 |
1804.4 |
378.7 |
556.7 |
0.4 |
2.6 |
0.005 |
|
31.7 |
2141.4 |
381.8 |
854.2 |
0.4 |
2.1 |
0.007 |
|
33.5 |
2816.4 |
386.1 |
1048.5 |
0.3 |
2.3 |
0.008 |
|
34.6 |
2558.3 |
388.3 |
805.2 |
0.3 |
2.7 |
0.006 |
|
42.7 |
2455.9 |
401 |
514.9 |
0.2 |
4 |
0.003 |
|
43.6 |
2619.4 |
402 |
861.8 |
0.3 |
2.6 |
0.005 |
Здесь первое значение относится к расчетам поля, выполненным с использованием для нахождения альфвеновского числа Маха M как параметра ∆R/RC, так и ρd/ρu — скачка плотности на фронте УВ (ρd — плотность плазмы за фронтом, ρu — перед фронтом УВ [Kim et al., 2012]). Второе значение среднего поля относится к расчетам поля с использованием для нахождения M только параметра ∆R/RC, как это делалось в нашей работе. Различие средних значений магнитного поля, полученных нами и в работе [Kim et al., 2012], обусловлено главным образом использованием в нашей работе упрощенной модели КВМ в трехмерном пространстве, включающей в себя такие упрощающие предположения, как радиальность движения КВМ, неизменность углового размера КВМ при движении, сферическая форма внешней границы тела КВМ и связанной с ним УВ и др. В то же время заметим, что это различие находится в пределах погрешности, с которой предложенный [Gopolswamy, Yashiro, 2011] метод в принципе позволяет определить величину магнитного поля в короне. На точность определения В влияет много факторов, включая используемые прибли- женные значения скорости медленного СВ, соотношения, позволяющие определить M (M связывается с параметром ∆R/RC или со скачком плотности плазмы на фронте УВ ρd/ρu), использование для всех событий одной и той же зависимости плотности плазмы от расстояния и т. д. Например, из рис. 2, б следует, что значения магнитного поля, рассчитанные с использованием связи числа Маха с параметром ∆R/RC, существенно меньше, чем значения B(R), полученные с использованием зависимости M от ρd/ρu.
На рис. 3, a показано рассеяние значений V A , полученных по данным наблюдений ГКВМ, а на рис. 3, б для сравнения показана зависимость V A от положения УВ из работы [Kim et al., 2012] . На рис. 3, в изображены зависимости от расстояния альфвенов-ской скорости V A , рассчитанные нами для медленного (нижняя полоса) и быстрого СВ (верхняя полоса) с использованием значений магнитного поля и концентрации протонов на орбите Земли и определенных зависимостей их изменения с расстоянием. Мы полагали, что в диапазоне расстояний 5 R S –1 а.е. (расстояние от Солнца до орбиты Земли) радиальная
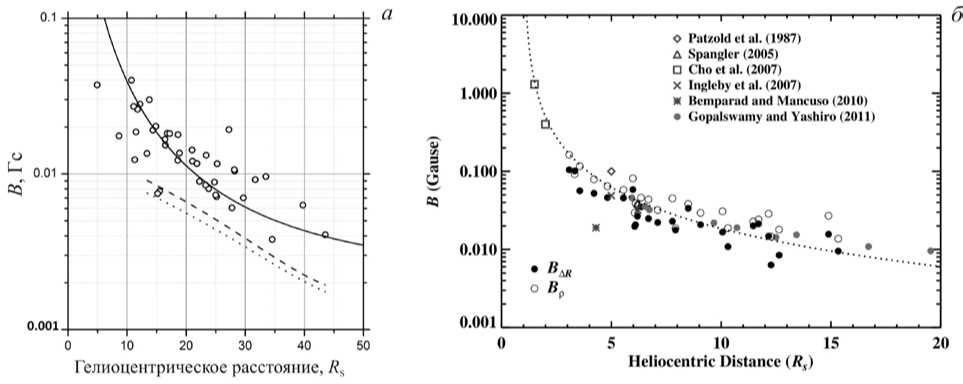
Рис. 2 . Панель а — значения магнитного поля B ( R ), полученные с помощью расчетов 3D-параметров ГКВМ в разные моменты времени для каждого рассмотренного события (кружки). Сплошная линия ( B R=11.1·10–5(215.5/( R / R S))2 Гс) — зависимость радиальной компоненты магнитного поля в горизонтальном участке медленного СВ от расстояния (детали см. в тексте в описании рис. 2). Две линии ниже — расчеты поля в предположении, что приосевая область КВМ движется в быстром СВ, скорость которого V SW=600 км/с (штрихи) и 800 км/с (пунктир) независимо от расстояния и с зависимостями концентрации протонов и радиальной компоненты магнитного поля от расстояния, характерными для быстрого СВ: n p=3(215.5/( R / R S))2 см–3, B R=3·10–5(215.5/( R / R S))2 Гс. Здесь приведены только линии регрессии. Панель б — рис. 8 из работы [Kim et al., 2012] (© AAS. Reproduced with permission): черные кружки — значения B ( R ), полученные из соотношения, связывающего число Маха с Δ R / R C, белые кружки — с отношением плотности на фронте УВ. Прочими символами показаны значения магнитной индукции, полученные другими методами разными авторами (см. [Kim et al., 2012] и цитируемую там литературу)
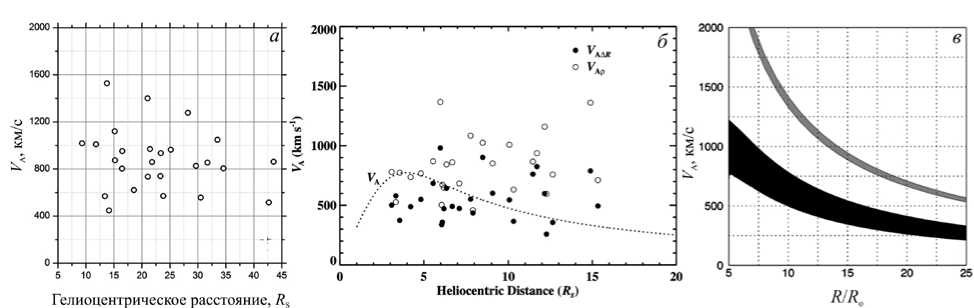
Рис. 3 . Панель a — рассеяние значений альфвеновской скорости V A (кружки) в зависимости от расстояния, полученных в 3D-пространстве по данным наблюдений ГКВМ. Панель б — рис. 7 из работы [Kim et al., 2012] (© AAS. Reproduced with permission): пунктир — зависимость V A( R ) из работы [Mann et al., 1999] ; черные кружки — значения B ( R ), полученные из соотношения, связывающего число Маха с Δ R / R C, белые кружки — с отношением плотности на фронте УВ. Панель в — зависимость V A( R ), полученная для медленного (черная полоса) и быстрого СВ (серая полоса) с использованием значений магнитного поля и концентрации протонов на орбите Земли и определенных зависимостей их изменения с расстоянием (см. [Fainshtein, Egorov, 2017] )
компонента магнитного поля B R ~1/ R 2 как в быстром, так и в медленном СВ, плотность протонов n p ~1/ R 2 в быстром СВ, а в медленном СВ меняется с расстоянием по закону, полученному для изменения концентрации электронов n e ( R ) в работе [Leblanc et al., 1998] . Детали построения зависимостей V A( R ) на рис. 3, в описаны в нашей работе [Fainshtein, Egorov, 2017] . Зависимости на рис. 3, в приведены для сравнения с рассеяниями точек на рис. 3, а , б потому, что зависимости на рис. 3, в являются, с нашей точки зрения, наиболее точными оценками V A( R ), сделанными к настоящему времени. Из рис. 3 следует, что в диапазоне расстояний (9– 15) R S среднее значение альфвеновской скорости
< V A >, полученное нами по данным наблюдений ГКВМ, составляет 938 км/с, а по данным работы [Kim et al., 2012] < V A >=709 км/с (559 км/с). В то же время на графике, построенном по данным наблюдений ГКВМ, более отчетливо наблюдается уменьшение альфвеновской скорости с расстоянием. Заметим также, что разброс значений V A для каждого положения УВ в диапазоне расстояний до 15 R S , полученный как в наших расчетах, так и в работе [Kim et al., 2012] , существенно больше по сравнению с расчетами альфвеновской скорости по данным измерений магнитного поля и плотности плазмы на орбите Земли (рис. 3, в ). Мы предполагаем, что это свидетельствует о более низкой точности расчетов
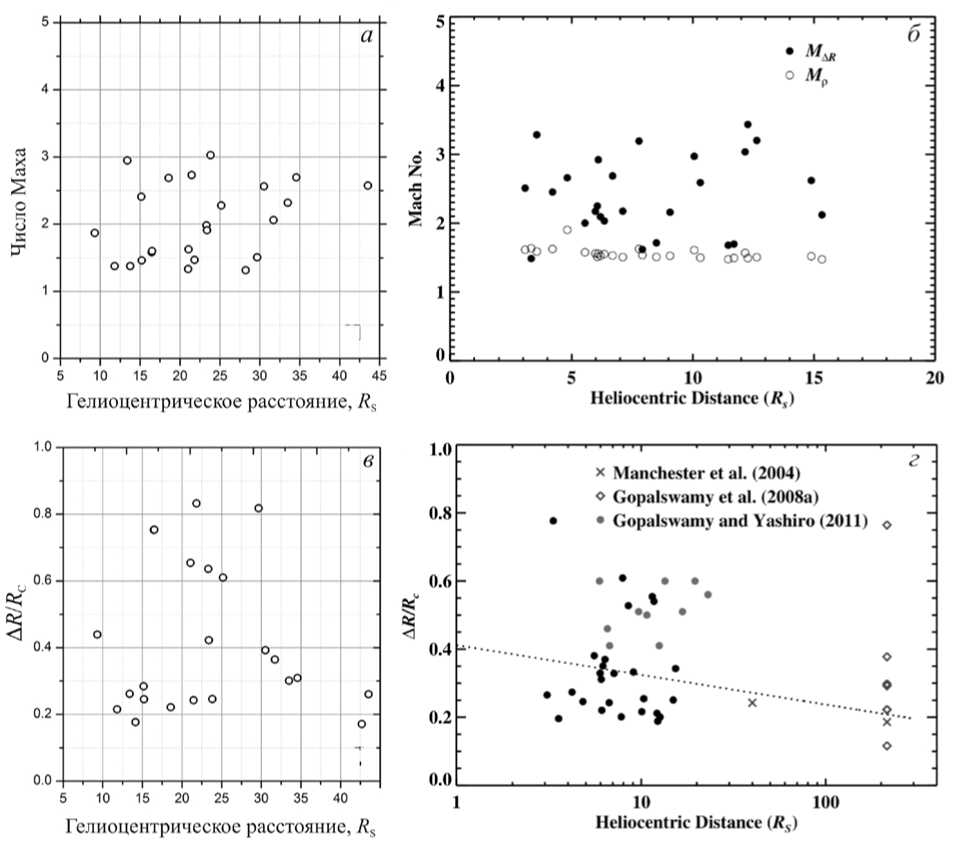
Рис. 4 . Панель а — рассеяние полученных нами значений числа Маха для различных положений УВ. Панель б — рис. 6 из работы [Kim et al., 2012] (© AAS. Reproduced with permission). Панель в — рассеяние полученных нами значений Δ R / R C, панель г — рис. 2 из [Kim et al., 2012] (© AAS. Reproduced with permission)
альфвеновской скорости с использованием методов, предложенных в работах [Gopalswamy, Yashiro, 2011; Kim et al., 2012] .
На рис. 4, а показано рассеяние полученных нами значений альфвеновского числа Маха M для различных положений УВ. На рис. 4, б показан аналогичный результат из работы [Kim et al., 2012] . Видно, что в диапазоне расстояний (9–15) R S разброс значений и среднее значение числа Маха М для двух типов расчетов близки: < M >=2.21 по нашим расчетам и < M >=2.03 (2.55) по результатам работы [Kim et al., 2012] . Напомним, что величина 2.55 получается при усреднении значений М , полученных с использованием только параметра ∆ R / R C , а величина 2.03 — с использованием как параметра Δ R / R C , так и скачка плотности плазмы ρ d /ρ u на фронте ударной волны.
На рис. 4, в показано полученное нами рассеяние значений ∆ R / R C для разных положений УВ, а на рис. 4, г — рассеяние того же параметра из работы [Kim et al., 2012] . В диапазоне расстояний (9–15) R S по нашим расчетам < ∆ R / R C >=0.39, по данным [Kim et al., 2012] < ∆ R / R C >=0.31.
ВЛИЯНИЕ СКОРОСТИ СОЛНЕЧНОГО ВЕТРА НА РАСЧЕТ ВЕЛИЧИНЫ МАГНИТНОГО ПОЛЯ
Как и работе [Gopalswamy, Yashiro, 2011], при проведении расчетов величины магнитного поля нами неявно предполагалось, что приосевые участки всех КВМ, свойства которых использовались для нахождения величины магнитного поля, движутся в области медленного СВ. Именно поэтому в качестве скорости СВ, по которому распространяется УВ, использовалась скорость медленного СВ с зависимостью от расстояния из работы [Sheeley et al., 1997]. В действительности для многих КВМ довольно сложно определить, какие части КВМ движутся в медленном СВ. Более того, в некоторых случаях весь КВМ может в поле зрения коронографа LASCO C3 двигаться в быстром СВ. При достаточно больших скоростях (например, больших 1500 км/с) впереди него может существовать УВ. Предположив, что во всех рассмотренных событиях КВМ движется в быстром СВ, мы с помощью метода [Go- palswamy, Yashiro, 2011] нашли радиальное распределение магнитного поля. Линии регрессии для зависимости магнитной индукции от положения УВ показаны на рис. 2. Видно, что в этом случае магнитное поле существенно меньше, чем в медленном СВ.
Отсюда следует, что расчетам радиальных распределений магнитного поля методом [Gopalswamy, Yashiro, 2011] должно предшествовать либо выяснение, какой участок КВМ движется в медленном СВ, а какой — в быстром, либо доказательство того, что весь КВМ движется в быстром СВ. Мы планируем, используя расчеты магнитного поля в потенциальном приближении и изображения белой короны по данным LASCO C2, C3, предложить возможный вариант решения этой задачи в нашей следующей работе. В частности, как отдельная группа будут рассмотрены КВМ, центральная часть которых движется вдоль участка пояса стримеров, приблизительно перпендикулярного плоскости неба, или, что то же самое, параллельного плоскости солнечного экватора (такие участки пояса стримеров или медленного СВ мы будем называть, как и в данной работе, горизонтальными участками). Участки пояса стримеров такого типа наблюдаются в поле зрения коронографа как яркие лучи, и в этом случае определение участка КВМ, движущегося в медленном СВ, не вызывает трудностей. Мы предлагаем также использовать еще один способ выделения лимбовых КВМ, центральная часть которых движется вдоль стримера, т. е. в области медленного СВ. Известно, что конфигурация пояса корональных стримеров в пространстве с хорошей точностью совпадает с конфигурацией нейтральной линии (НЛ) магнитного поля на поверхности источника, которая получается из расчетов поля в потенциальном приближении [Schwenn, Marsch, 1990] . Обычно радиус поверхности источника варьирует в расчетах поля в диапазоне (1.6–3.25) R S. Отсюда следует, что участкам пояса стримеров, примерно перпендикулярным плоскости неба, соответствуют участки НЛ, приблизительно параллельные плоскости экватора. Если в момент наблюдения КВМ в поле зрения коронографа LASCO C2 над соответствующим лимбом окажется близкий к середине участок НЛ, приблизительно параллельный плоскости экватора, а ось КВМ при этом будет близка по широте к широте этого участка, можно быть уверенными, что значительная часть КВМ будет двигаться в медленном СВ.
На рис. 5 показаны рассчитанная в WSO [http://wso. ] НЛ с участками, расположенными под малыми углами к плоскости солнечного экватора (т. е. почти параллельными этой плоскости), и КВМ, движущийся вдоль яркого стримера, соответствующего одному из таких участков, а значит, центральная его часть движется в области медленного СВ. Заметим, что этот подход для выделения КВМ, большая часть которого движется в медленном СВ, можно применить и для КВМ, летящих в направлениях, близких к оси Солнце—Земля. В этом случае, используя, например, модель ice-cream cone для КВМ, найдем направление движения модельного КВМ и сравним широту этого направления с широтой рассчитанного в потенциальном приближении горизонтального участка НЛ на поверхности источника в день наблюдения КВМ (если такой участок существует!). Если широта направления движения КВМ и широта горизонтального участка НЛ близки, то все выводы, которые мы сделали для лимбового события на рис. 5, справедливы и в этом случае: большая часть такого КВМ будет двигаться в медленном СВ.
ВЫВОДЫ
-
1. С использованием метода, предложенного [Gopalswamy, Yashiro, 2011] , а затем развитого в [Kim et al., 2012] , получено пространственное распределение магнитного поля B ( R ) приблизительно вдоль оси Солнце—Земля. Для этого использовались данные о гало-КВМ (ГКВМ), источники большинства которых были расположены вблизи центра солнечного диска.
-
2. Необходимые для расчета величины магнитного поля параметры ГКВМ в трехмерном пространстве находились с помощью модели ice-cream cone для КВМ [Xue et al., 2005] .
-
3. Были использованы новые подходы для расчетов параметров модели ice-cream cone. В отличие от работы [Xue et al., 2005] в настоящей работе: а) параметры модельного КВМ в трехмерном пространстве рассчитывались отдельно для тела КВМ и связанной с ним УВ; б) рассчитывались не только скорости указанных структур, но и их положения вдоль направления движения модельного КВМ в трехмерном пространстве в разные моменты времени; в) граница проекции тела КВМ и УВ на плоскость неба выделялась не только дискретным набором точек на этих структурах, но и аппроксимацией этих структур эллипсами или участками эллипсов.
-
4. С помощью таких расчетов поля нам удалось удвоить максимальное расстояние, по сравнению с работами [Gopalswamy, Yashiro, 2011; Kim et al., 2012] , до которого было найдено распределение магнитного поля B ( R ): примерно с 21 R S до 43 R S .
-
5. Показано, что полученное нами распределение B ( R ) в среднем близко к зависимости от расстояния радиальной компоненты поля, меняющейся по закону B R = B RE (215.5/( R / R S ))2, где B RE =11·10–5 Гс — возможное значение B R в горизонтальном участке медленного СВ на орбите Земли (о горизонтальных участках медленного СВ см. в работе [Fainshtein, 1991] ).
-
6. Относительно близкими (с различием в пределах ~5–26 %) оказались полученные в настоящей работе и в статье [Kim et al., 2012] в интервале (9–15) R S средние значения магнитного поля B , аль-фвеновской скорости V A, альфвеновского числа Маха М и параметра ∆ R / R C . При этом рассчитанные нами значения B , V A и М сравнивались с суммарными результатами [Kim et al., 2012] , полученными с использованием соотношений между числом Маха и параметрами как ∆ R / R С , так и ρ d /ρ u .
-
7. Распределения B ( R ), найденные предложенным нами способом вдоль направления, близкого к оси Солнце—Земля, могут быть использованы: а) для оценок магнитного поля на орбите Земли по солнечным данным для каких-то характерных интервалов времени (например, для разных фаз солнечной актив-
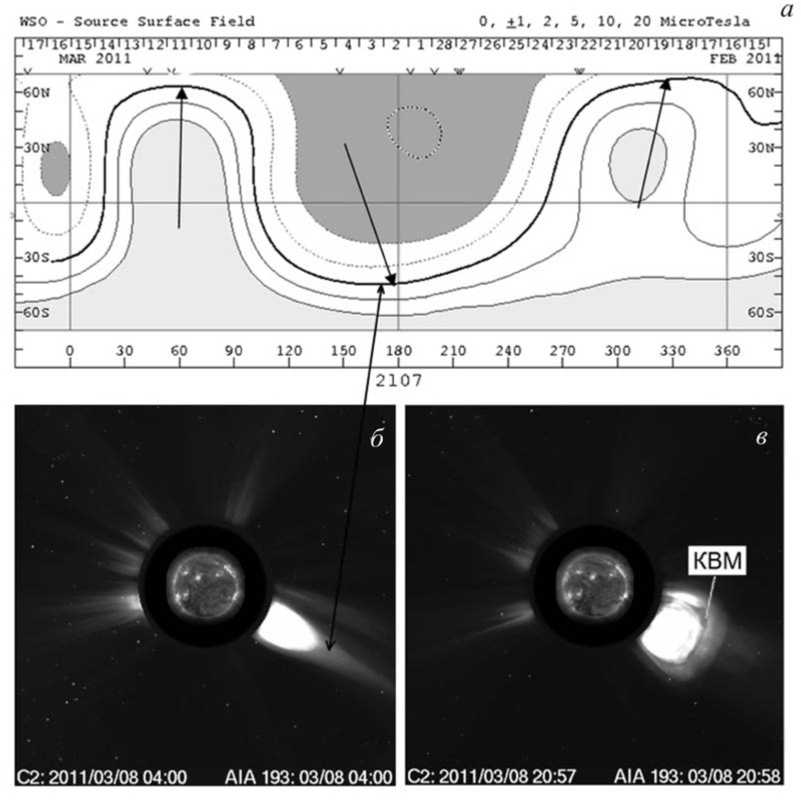
Рис. 5. Панель a — распределение магнитного поля на поверхности источника (2.5RS) по данным расчетов поля в потенциальном приближении в WSO []. Стрелками указаны участки НЛ, расположенные под малыми углами к плоскости солнечного экватора. Воздействие КВМ на стример привело к уменьшению его яркости впереди КВМ. Изображения белой короны по данным LASCO C2 (б, в): б — корональный стример до появления КВМ (указан стрелкой) и соответствующий этому стримеру участок НЛ; в — КВМ, средняя часть которого движется по корональному стримеру, показанному на панели б
ности); б) для сравнения с радиальными распределениями поля, полученными с использованием МГД-расчетов. И, наконец, заметим, что вполне удовлетворительное согласие наших расчетов магнитного поля с расчетами [Kim et al., 2012] является дополнительным основанием считать, что модель icecream cone для КВМ позволяет вполне адекватно находить как характеристики самого КВМ, так и характеристики его движения в трехмерном пространстве.
-
8. Полученные нами и в работе [Kim et al., 2012] радиальные распределения V A ( R ) были сопоставлены с радиальной зависимостью альфвеновской скорости в медленном СВ из работы [Fainshtein, Egorov, 2017] , которую авторы считают наиболее точной (в пределах погрешности определения V A ( R )) из известных зависимостей (например, по сравнению с популярной у исследователей зависимостью V A( R ) из работы [Mann et al., 1999] ). Сделан вывод, что наибольшие значения V A , найденные как в данной работе, так и в работе [Kim et al., 2012] , завышены по сравнению с реальными значениями альфвеновской скорости.
-
9. Предложен способ выделения КВМ, значительная часть которых движется в области медленного СВ.
Авторы благодарны команде LASCO за возможность свободного использования данных коронографа. Работа выполнена в рамках Плана НИР ИСЗФ СО РАН на 2016–2018 гг. II.16.1.6. «Геоэффективные процессы в хромосфере и короне Солнца» (базовый проект) и при частичной поддержке грантов РФФИ № 15-02-01077-а и № 16-32-00315.
Список литературы Радиальные распределения величины магнитного поля в солнечной короне, полученные с использованием сведений о быстрых ГАЛО-КВМ
- Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков. М.: Атомиздат, 1979. 320 с.
- Ландау Л.Д., Лифшиц В.М. Гидродинамика. М.: Наука, 1988. 733 с.
- Bemporad A., Mancuso S. First complete deter-mination of plasma physical parameters across a coronal mass ejection-driven shock//Astrophys. J. 2010. V. 720. P. 130-143 DOI: 10.1088/0004-637X/720/1/130
- Brueckner G.E., Howard R.A., Koomen M.J., et al. The Large Angle Spectroscopic Coronagraph (LASCO)//Solar Phys. 1995. V. 162. P. 357-402 DOI: 10.1007/BF00733434
- Bogod V.M., Yasnov L.V. Determination of the structure of the coronal magnetic field using microwave polarization measurements//Solar Phys. 2016. V. 291. P. 3317-3328.
- Cho K.-S., Lee J., Gary D.E., et al. Magnetic field strength in the solar corona from type II band splitting//Astrophys. J. 2007. V. 665, N 1. P. 799.
- Fainshtein V.G. The interaction effect of fast and slow solar wind streams in interplanetary space on wind characteristics at the Earth’s orbit//Solar Phys. 1991. V. 136. P. 169-189
- DOI: 10.1007/BF00151702
- Fainshtein V.G. Method for determining the parameters of full halo coronal mass ejections//Geomagnetism and Aeronomy. 2006. V. 46, iss. 3. P. 339-349. 9320603008X
- DOI: 10.1134/S00167
- Fainshtein V.G., Egorov Ya.I. Origin of a CME-related shock within the LASCO C3 field-of-view//Eprint arXiv. 2017. arXiv:1712.09051.
- Gopalswamy N., Yashiro S. The strength and radial profile of the coronal magnetic field from the standoff distance of a coronal mass ejection-driven shock//Astrophys. J. Lett. 2011. V. 736, article id. L17. 5 p
- DOI: 10.1088/2041-8205/736/1/L17
- Gopalswamy N., Akiyama S., Yashiro S., et al. Solar sources and geospace consequences of interplanetary magnetic clouds observed during solar cycle 23//J. Atmos. Solar-Terr. Phys. 2008. V. 70. P. 245.
- Howard R.A., Moses J.D., Vourlidas A., et al. Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI)//Space Sci. Rev. 2008. V. 136, iss. 1-4. P. 67-115. 10.1007/s11214-008-9341-4
- DOI: :10.1007/s11214-008-9341-4
- Ingleby L.D., Spangler S.R., Whiting C.A. Probing the Large-scale plasma structure of the solar corona with Faraday rotation measurements//Astrophys. J. 2007. V. 668. P. 520.
- Kaiser M.L., Kucera T.A., Davila J.M., et al. The STEREO mission: an introduction//Space Sci. Rev. 2008. V. 136. P. 5-16
- DOI: 10.1007/s11214-007-9277-0
- Kim T., Moon Y., Na H. Comparison of CME radial velocities from a flux rope model and an ice cream cone model//American Geophysical Union, Fall Meeting 2011, abstract #SH51A-1992.
- Kim R.-S., Gopalswamy N., Moon Y.-J., et al. Magnetic field strength in the upper solar corona using white-light shock structures surrounding coronal mass ejections//Astrophys. J. 2012. V. 746, article id. 118. 8 p. 10.1088/0004-637X/746/2/118
- DOI: :10.1088/0004-637X/746/2/118
- Leblanc Y., Dulk G.A., Bougeret J.-L. Tracing the electron density from the corona to 1 au//Solar Phys. 1998. V. 183. P. 165-180
- DOI: 10.1023/A:1005049730506
- Lee J. Radio emissions from solar active regions//Space Sci. Rev. 2007. V. 133. P. 73-102
- DOI: 10.1007/s11214-007-9206-2
- Lin H., Penn M.J., Tomczyk S. A new precise measurement of the coronal magnetic field strength//Astrophys. J. 2000. V. 541. P. L83-L86
- DOI: 10.1086/312900
- Manchester W.B., Gombosi T.I., Roussev I., et al. Modeling a space weather event from the Sun to the Earth: CME generation and interplanetary propagation//J. Geophys. Res.: Space Phys. 2004. V. 109, A02107.
- Mann G., Klassen A., Estel C., Thompson B.J. Coronal transient waves and coronal shock waves//8th SOHO Workshop "Plasma dynamics and diagnostics in the solar transition region and corona": Proc. Paris, 1999. P. 477-481.
- Michalek G. An asymmetric cone model for halo coronal mass ejections//Solar Phys. 2006. V. 237, iss. 1. P. 101-118
- DOI: 10.1007/s11207-006-0075-8
- Pӓtzold M., Bird M.K., Volland H., et al. The mean coronal magnetic field determined from HELIOS Faraday rotation measurements//Solar Phys. 1987. V. 109. P. 9-105. 10.1007/BF00167401
- DOI: :10.1007/BF00167401
- Poomvises W., Gopalswamy N., Yashiro S., et al. Determination of the heliospheric radial magnetic field from the standoff distance of a CME-driven shock observed by the STEREO spacecraft//Astrophys. J. 2012. V. 758, article id. 118. 6 p
- DOI: 10.1088/0004-637X/758/2/118
- Rudenko G.V. Extrapolation of the solar magnetic field within the potential-field approximation from full-disk magnetograms//Solar Phys. 2001. V. 198. P. 5-30. 10.1023/A:1005270431628
- DOI: :10.1023/A:1005270431628
- Rudenko G.V., Myshyakov I.I. Analysis of reconstruction methods for nonlinear force-free fields//Solar Phys. 2009. V. 257. P. 287-304
- DOI: 10.1007/s11207-009-9389-7
- Russell C.T., Mulligan T. On the magnetosheath thicknesses of interplanetary coronal mass ejections//Planet. Space Sci. 2002. V. 50. P. 527-534. ) 00031-4
- DOI: 10.1016/S0032-0633(02
- Sahal-Bréchot S., Malinovsky M., Bommier V. The polarization of the O VI 1032 Å//Astron. Astrophys. 1986. V. 168. P. 284-300.
- Sheeley N.R., Jr., Wang Y.-M., Hawley S.H., et al. Measurements of flow speeds in the corona between 2 and 30 R//Astrophys. J. 1997. V. 484. P. 472-478
- DOI: 10.1086/304338
- Sheeley N.R., Hakala W.N., Wang Y.-M. Detection of coronal mass ejection associated shock waves in the outer corona//J. Geophys. Res. 2000. V. 105.P. 5081-5092
- DOI: 10.1029/1999JA000338
- Schmidt J.M., Cairns I.H., Gopalswamy N., Yashiro S. Coronal magnetic field profiles from shock-CME standoff distances//J. Geophys. Res.: Space Phys. 2016. V. 121. P. 9299-9315
- DOI: 10.1002/2016JA022956
- Schwenn R., Marsch E. (Eds.) Physics of the Inner Heliosphere I. Large-Scale Phenomena. Springer-Verlag, 1990. 293 p
- DOI: 10.1007/978-3-642-75361-9
- Spangler S.R. The strength and structure of the coronal magnetic field//Space Sci. Rev. 2005. V. 121. P. 189-200
- DOI: 10.1007/s11214-006-4719-7
- Thernisien A.F.R., Howard R.A., Vourlidas A. Modeling of flux rope coronal mass ejections//Astrophys. J. 2006. V. 652. P. 763-773
- DOI: 10.1086/508254
- Wiegelmann T. Nonlinear force-free modeling of the solar coronal magnetic field//J. Geophys. Res. 2008. V. 113. A03S02
- DOI: 10.1029/2007JA012432
- Xue X.H., Wang C.B., Dou X.K. An ice-cream cone model for coronal mass ejections//J. Geophys. Res.: Space Phys. 2005. V. 110, iss. A8, A08103
- DOI: 10.1029/2004JA010698
- URL: https://cdaw.gsfc.nasa.gov/CME_list/HALO/halo.html (дата обращения 16 сентября 2017 г.).
- URL: http://wso.stanford.edu/synsourcel.html (дата обращения 16 сентября 2017 г.).
- URL: http://wso.stanford.edu/synoptic/WSO-S.2107.gif (дата обращения 16 сентября 2017 г.).
- Artsimovich L.A., Sagdeev R.Z. Fizika plazmy dlya fizikov . Moscow, Atomizdat. 1979, 320 p..
- Bemporad A., Mancuso S. First complete determination of plasma physical parameters across a coronal mass ejection-driven shock. Astrophys. J. 2010, vol. 720, pp. 130-143
- DOI: 10.1088/0004-637X/720/1/130
- Brueckner G.E., Howard R.A., Koomen M.J., Korendyke C.M., Michels D.J., Moses J.D. The Large Angle Spectroscopic Coronagraph (LASCO). Solar Phys. 1995, vol. 162, pp. 357-402
- DOI: 10.1007/BF00733434
- Bogod V.M., Yasnov L.V. Determination of the structure of the coronal magnetic field using microwave polarization measurements. Solar Phys. 2016, vol. 291, pp. 3317-3328.
- Cho K.-S., Lee J., Gary D.E., Moon Y.-J., Park Y.D. Magnetic field strength in the solar corona from type II band splitting. Astrophys. J. 2007, vol. 665, p. 799.
- Fainshtein V.G. The interaction effect of fast and slow solar wind streams in interplanetary space on wind characteristics at the Earth’s orbit. Solar Phys. 1991, vol. 136, pp. 169-189
- DOI: 10.1007/BF00151702
- Fainshtein V.G. Method for determining the parameters of full halo coronal mass ejections. Geomagnetism and Aeronomy. 2006, vol. 46, iss. 3, pp. 339-349. 0603008X
- DOI: 10.1134/S00167932
- Fainshtein V.G., Egorov Ya.I. Origin of a CME-related shock within the LASCO C3 field-of-view. Eprint arXiv.2017. arXiv:1712.09051.
- Gopalswamy N., Yashiro S. The strength and radial profile of the coronal magnetic field from the standoff distance of a coronal mass ejection-driven shock. Astrophys. J. Lett. 2011, vol. 736, article id. L17, 5 p. 1/L17
- DOI: 10.1088/2041-8205/736/
- Gopalswamy N., Akiyama S., Yashiro S., Michalek G., Lepping R.P. Solar sources and geospace consequences of interplanetary magnetic clouds observed during solar cycle 23. J. Atmos. Solar-Terr. Phys. 2008, vol. 70, p. 245.
- Howard R.A., Moses J.D., Vourlidas A., et al. Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI). Space Sci. Rev. 2008, vol. 136, iss. 1-4. pp. 67-115. 10.1007/s11214-008-9341-4
- DOI: :10.1007/s11214-008-9341-4
- Ingleby L.D., Spangler S.R., Whiting C.A. Probing the large-scale plasma structure of the solar corona with Faraday rotation measurements. Astrophys. J. 2007, vol. 668, p. 520.
- Kaiser M.L., Kucera T.A., Davila J.M., St. Cyr O.C., Guhathakurta M., Christian E. The STEREO mission: an introduction. Space Sci. Rev. 2008, vol. 136, pp. 5-16. 10.1007/s11214-007-9277-0
- DOI: :10.1007/s11214-007-9277-0
- Kim T., Moon Y., Na H. Comparison of CME radial velocities from a flux rope model and an ice cream cone model. American Geophysical Union, Fall Meeting 2011, abstract #SH51A-1992.
- Kim R.-S., Gopalswamy N., Moon Y.-J., Cho K.-S., Yashiro S. Magnetic field strength in the upper solar corona using white-light shock structures surrounding coronal mass ejections. Astrophys. J. 2012, vol. 746, article id. 118, 8 p. 10.1088/0004-637X/746/2/118
- DOI: :10.1088/0004-637X/746/2/118
- Landau L.D., Lifshitz E.M. Gidrodinamika . 1988, 733 p..
- Leblanc Y., Dulk G.A., Bougeret J.-L. Tracing the electron density from the corona to 1 au. Solar Phys. 1998, vol. 183, pp. 165-180
- DOI: 10.1023/A:1005049730506
- Lee J. Radio emissions from solar active regions. Space Sci. Rev. 2007, vol. 133, pp. 73-102
- DOI: 10.1007/s11214-007-9206-2
- Lin H., Penn M.J., Tomczyk S. A new precise measurement of the coronal magnetic field strength. Astrophys. J. 2000, vol. 541, pp. L83-L86
- DOI: 10.1086/312900
- Manchester W.B., Gombosi T.I., Roussev I., Ridley A., de Zeeuw D.L., Sokolov I.V., Powell K.G., Tóth G. Modeling a space weather event from the Sun to the Earth: CME generation and interplanetary propagation. J. Geophys. Res.: Space Phys. 2004, vol. 109, A02107.
- Mann G., Klassen A., Estel C., Thompson B.J. Coronal transient waves and coronal shock waves. 8th SOHO Workshop "Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona": Proc. Paris, 1999, pp. 477-481.
- Michalek G. An asymmetric cone model for halo coronal mass ejections. Solar Phys. 2006, vol 237, iss. 1, pp. 101-118
- DOI: 10.1007/s11207-006-0075-8
- Pӓtzold M., Bird M.K., Volland H., Levy G.S., Seidel B.L., Stelzried C.T. The mean coronal magnetic field determined from HELIOS Faraday rotation measurements. Solar Phys. 1987, vol. 109, pp. 9-105. 10.1007/BF00167401
- DOI: :10.1007/BF00167401
- Poomvises W., Gopalswamy N., Yashiro S., Kwon R.-Y., Olmedo O. Determination of the heliospheric radial magnetic field from the standoff distance of a CME-driven shock observed by the STEREO spacecraft. Astrophys. J. 2012, vol. 758, article id. 118, 6 p
- DOI: 10.1088/0004-637X/758/2/118
- Rudenko G.V. Extrapolation of the solar magnetic field within the potential-field approximation from full-disk magnetograms. Solar Phys. 2001, vol. 198, pp. 5-30. 10.1023/A:1005270431628
- DOI: :10.1023/A:1005270431628
- Rudenko G.V., Myshyakov I.I. Analysis of reconstruction methods for nonlinear force-free fields. Solar Phys. 2009, vol. 257, pp. 287-304
- DOI: 10.1007/s11207-009-9389-7
- Russell C.T., Mulligan T. On the magnetosheath thicknesses of interplanetary coronal mass ejections. Planet. Space Sci. 2002, vol. 50, pp. 527-534. ) 00031-4
- DOI: 10.1016/S0032-0633(02
- Sahal-Bréchot S., Malinovsky M., Bommier V. The polarization of the O VI 1032 Å. Astron. Astrophys. 1986, vol. 168, pp. 284-300.
- Sheeley N.R., Jr., Wang Y.-M., Hawley S.H., et al. Measurements of flow speeds in the corona between 2 and 30 R. Astrophys. J. 1997, vol. 484, pp. 472-478
- DOI: 10.1086/304338
- Sheeley N.R., Hakala W.N., Wang Y.-M. Detection of coronal mass ejection associated shock waves in the outer corona. J. Geophys. Res. 2000, vol. 105, pp. 5081-5092
- DOI: 10.1029/1999JA000338
- Schmidt J.M., Cairns I.H., Gopalswamy N., Yashiro S. Coronal magnetic field profiles from shock-CME standoff distances. J. Geophys. Res.: Space Phys. 2016, vol. 121, pp. 9299-9315
- DOI: 10.1002/2016JA022956
- Schwenn R., Marsch E. (Eds.) Physics of the Inner Heliosphere I. Large-Scale Phenomena. Springer-Verlag, 1990, 293 p
- DOI: 10.1007/978-3-642-75361-9
- Spangler S.R. The strength and structure of the coronal magnetic field. Space Sci. Rev. 2005, vol. 121, pp. 189-200
- DOI: 10.1007/s11214-006-4719-7
- Thernisien A.F.R., Howard R.A., Vourlidas A. Modeling of flux rope coronal mass ejections. Astrophys. J. 2006, vol. 652, pp. 763-773
- DOI: 10.1086/508254
- Wiegelmann T. Nonlinear force-free modeling of the solar coronal magnetic field. J. Geophys. Res. 2008, vol. 113, A03S02
- DOI: 10.1029/2007JA012432
- Xue X.H., Wang C.B., Dou X.K. An ice-cream cone model for coronal mass ejections. J. Geophys. Res.: Space Phys. 2005, vol. 110, iss. A8, CiteID A08103
- DOI: 10.1029/2004JA010698
- URL: https://cdaw.gsfc.nasa.gov/CME_list/HALO/halo.html (accessed September 16, 2017).
- URL: http://wso.stanford.edu/synsourcel.html (accessed September 16, 2017).
- URL: http://wso.stanford.edu/synoptic/WSO-S.2107.gif (accessed September 16, 2017).


