Радиобиологическая модель расчёта вероятности гибели клеток млекопитающих при облучении их ионизирующим излучением с разной линейной потерей энергии

Одной из фундаментальных проблем радиобиологии является прогнозирование вероятности возникновения радиационно-индуцированных эффектов у биологических объектов в результате воздействия на них произвольно заданным ионизирующим излучением (ИИ) в произвольно заданных условиях (вид ионизирующих частиц (ИЧ), их энергия, временной режим, наличие модифицирующих факторов) [1-9].

Целью данной работы является решение частной задачи общей проблемы: разработка математической модели вероятности гибели клеток млекопитающих в зависимости от дозы ИИ с произвольно заданными линейными потерями энергии (ЛПЭ), при однократном облучении этих клеток in vitro . Для решения поставленной задачи использованы микродозиметрические подходы, основанные на теории дуального действия радиации.

Формально задача ставится следующим образом. Считается известной экспериментально определённая вероятность гибели клеток млекопитающих в зависимости от дозы облучения их заданным одним видом ИЧ, например, гамма-квантами с энергией 250 кэВ. Требуется теоретически рассчитать вероятность гибели выбранных клеток в зависимости от дозы ИИ с произвольно заданными ЛПЭ.

Такая задача была поставлена в начале прошлого века, но до сих пор остаётся не решённой. В работе предлагается и обосновывается модель действия ИИ разного качества, позволяющая прогнозировать вероятность гибели клеток млекопитающих в зависимости от дозы при однократном облучении их in vitro . Качество излучения задаётся ЛПЭ – потерей энергии ионизирующей частицы на единицу длины пробега (линейной потерей энергии). В предложенной модели удалось разделить биологические параметры, ответственные за появление радиационно-индуцированного эффекта, от радиационных характеристик условий облучения и, таким образом, решить поставленную задачу.

Для обоснования модели авторы специально использовали классические радиобиологические данные, лежащие в основе рекомендаций МАГАТЭ по определению относительной биологической эффективности (ОБЭ) ИИ разного качества.

Материалы и методы

В работе в качестве радиационно-индуцированного эффекта рассматривается гибель клеток. Для решения поставленной задачи использован подход, предложенный A.M. Kellerer и H.H. Rossi [1-3] при разработке микродозиметрических моделей, в частности, теории дуального действия.

Описание и проверка модели

Основные положения модели. Считается, что в клетке имеется область поражения (ОП) – шар с диаметром L. Область поражения не является однородной. Считается, что в ОП имеются чувствительные объёмы (ЧО), повреждение которых может привести к наблюдаемому радиационно-индуцированному эффекту (гибели клетки). Вероятность гибели клетки зависит от числа повреждённых ЧО. Вероятность повреждения ЧО зависит от энергии, поглощённой в нём. В предлагаемой модели считается, что все ЧО одинаковы по всем показателям.

Для расчёта энергии, поглощённой в ЧО, использовалась достаточно простая модель взаимодействия ИЧ с веществом: частицы двигаются по прямой, ЛПЭ частицей совпадают с линейной энергией, поглощаемой в веществе (не учитывается структура трека ИЧ).

В предлагаемой модели считается, что: источник ИЧ находится вне ОП на расстоянии большем, чем в 3 диаметра ОП; ИЧ двигается по прямой; ЛПЭ не меняется при прохождении ИЧ через ОП; число поражённых ЧО пропорционально длине пробега ИЧ в ОП; пробег ИЧ много больше размеров ОП (ИЧ не останавливается в ОП).

При одном событии поглощения энергии в ОП может поражаться разное число ЧО. Если ЧО распределены по объёму ОП равномерно, то число поражённых ЧО пропорционально длине пробега частицы ( x ) в ОП. Количество поражённых в одном событии поглощения энергии в ЧО ( K 11 ) зависит от распределения длин пробегов ИЧ ( µ ( x )) в ОП.

K_ii = ах ]^^максд(х) xxdx = axx ,                                            (1)

где a =const не зависит от характеристик поля излучения; X - средняя длина пробега ИЧ в ОП.

Отсюда следует, что в случае одинакового распределения длин пробегов ИЧ разного вида и разной энергией в ОП K 11 будет одинаковым.

Формализация модели. Считается, что вероятность гибели клетки η (D) однозначно связана со средним числом повреждённых ЧО и представляется функцией (2):

^(D) = I-exp(-A xK_p(D)) ,                                               (2)

где η (D) – вероятность гибели клетки при дозе D ; K p (D) – среднее число повреждённых ЧО в ОП клетки, определяется выражением (3); А =const и не зависит от характеристик поля излучения.

K_p(D) = Z” i P i (D) Т^Кц х S j ) ,                                                (3)

где P i (D) – вероятность того, что в ОП произойдёт i событий при дозе D ; K ij – среднее число поражённых ЧО (не обязательно повреждённых), в которых произошло j событий, если в ОП произошло i событий; S j – вероятность повреждения ЧО, если в нём произошло j событий поглощения энергии.

Так как по предположению события в ОП происходят независимо друг от друга, P i (D) подчиняется закону Пуассона [1, 2]:

Pt(D) = (иоп/Д! х exp(-non),(4)

где и_ОП - среднее число событий в ОП.

поп = D/z1oп, где D - доза; z10П - средняя удельная энергия, поглощённая в ОП в одном событии [2, 3].

гюп^^^ЛПЭх^ср^ЛПЭ/а,(6)

М0П          МОП где ё1ОП - средняя поглощённая энергия в ОП клетки при одном событии поглощения энергии, произошедшем в ОП; MОП – масса ОП; Lср – средний пробег ИЧ в ОП.

Величина z_10П зависит от размеров ОП, который неизвестен, и от ЛПЭ.

и_0П = aD/ЛПЭ .                                                                    (7)

При заданных условиях облучения α =const, не зависит от радиационных характеристик и является свободным параметром, учитывающим геометрические параметры и плотность ОП. K ij – среднее число поражённых ЧО, в которых произошло j событий, если в ОП произошло i событий. По определению при прохождении одной ИЧ через ОП среднее число поражённых ЧО равно среднему числу событий в ЧО. K 11 – среднее число событий в ЧО при одном событии в ОП. При одном событии в ОП может поражаться несколько ЧО. J 1 – среднее число событий в ЧО при одном событии в ОП.

K ii=h .                                                                              (8)

Если в ОП произошло i событий, то среднее суммарное число событий в ЧО:

J t = ixJ i .                                                                                      (9)

Так как в отдельных ЧО может произойти 1, 2, …, i событий, то, учитывая (8) и (9):

^Ку — ^{J х Г}у — ' ^{х Г}у ^{х К}и >                                                    ⁽¹⁰⁾

где r y - вероятность j событий в одном ЧО, если в ОП произошло i событий.

Так как по предположению события в ОП происходят независимо друг от друга, то приходим к стандартной задаче распределения бросаемых шариков по лункам, решением которой является биноминальное распределение:

r_t) — с ' х r i х (1 - г) ' ^- ' ,                                                                      (11)

где r - вероятность события в заданном ЧО, r =const, т.к. все ЧО считаются одинаковыми; С ' - коэффициенты разложения бинома Ньютона.

Преобразование выражения (3) с учётом (5), (10) приводит к следующему выражению:

K_P(D) — T^i P^D^ i Ri j S j — Е Г=1 й оп' /'! х ехр(-й_оп) х Е’^К^

= ехр(-й оп ) х Z” 1 {^ х E ‘=i [i х Иц х C ' х г ' х (1- г) ' ^- ' х S_y]} .                     (12)

Учитывая, что C 1 =1; C 1 =2; C 2 =1 и разложение функции ехр(-й_оп) в ряд:

ехр(-й оп ) — 1-^+1/2х (  ) ² -_,                                     (13)

получаем:

^(D) —[1-^- + 1х(^-)2--]хгх{ z   о pV 7 L    Z1on   2   kZ1on/       J          J ( D у

I V Z1on/

х К 11 5 1 +

^ЮП х K11((1 — r)51 + r52) + "-

} •      ⁽¹⁴⁾

Известно, что экспериментальная зависимость вероятности гибели клеток млекопитающих от дозы хорошо описывается линейно-квадратичной моделью (LQ-модель) [3, 6-9], которая имеет вид:

p(D) — 1 - ехр(-а₁ х D - а₂ х D²) ,

где n (D) - вероятность гибели клетки при дозе D ; a i , а г - биологические параметры модели, связывающие вероятность радиационно-индуцированного эффекта (гибели клетки) с дозой облучения.

Сравнение (1) и (15) показывает, что:

Л х K_p(D) — а₁ х D + а₂ х D² .

Отсюда следует, что в выражении (3) можно ограничиться только членами, содержащими D и D² . Формально это означает, что можно рассматривать только ЧО, в которых произошло одно или два события поглощения энергии.

Перемножив многочлены в выражении (16) и ограничиваясь членами, содержащими D и D² , получим (17):

K p (D) — (Иц х 5 1 /Z 1on ) х rD + Иц х г²($ 2 - 5 1 )/ z^ n х D².

Отсюда следует, что:

I

— АхК11 х51 х^- z1on

— Ах К_Х1 х 5, х г² х (—

'51

-

^1)/z 1on

или

{

5i — К1 х z1on

3 2 — ~ х Г Н² - 1)

^z 1on      V^S1     /

где K i =A х K 11 x r - свободный параметр модели; S i - вероятность того, что при одном событии поражения ЧО будет повреждён; S 2 – вероятность того, что при двух событиях в нём ЧО будет повреждён; z_10n - средняя удельная энергия, поглощённая в ОП в одном событии.

Выражения (19) для а 1 и а 2 являются формальным представлением предлагаемой модели.

Вероятность повреждения чувствительного объёма. S j – вероятность повреждения ЧО, если в нём произошло j событий поглощения энергии. В данной работе считается, что вероятность возникновения повреждения ф ( е ) зависит от поглощённой энергии е и для всех ЧО фе ) одинакова. В этом случае:

Sj = j^tofjtodE,(20)

где f j (е) d £ - вероятность того, что в результате j событий в ЧО поглотится энергия [ е, е + d£ ]; ф(е) - вероятность того, что при поглощении энергии е ЧО будет повреждён.

Некоторые свойства функций f j ( e ) , которые будут использованы дальше [3]:

;0”/у(е)4Е = 1для j=1,2 (21)

fj(£) = /о” fj-i(t)fi(£ — t)dt.(22)

Физические характеристики модели (поглощение энергии при прохождении ИЧ через ОП и ЧО). Физическими характеристиками предлагаемой модели (19) являются z_10n , f i ( e ) и f 2 ( e ) . В [4] показано, что в рамках принятых упрощений распределение длин пробегов в шаре p (x) = C i x x , где 0< x < Х макс , c i =const, а также, что e = C 2 x x .

Отсюда следует, что для ЧО с учётом нормировки:

/ 1 (е) = {

'^{2 x}          при ⁰ <  ^£ <  ^£ _MaKC

^Е макс

0         £ < о И Е> Емакс где емакс - верхняя оценка максимальной энергии, поглощённой в ЧО, при прохождении одной частицы.

Е макс = y x l ,                                                                                           (24)

где y =ЛПЭ; l – диаметр ЧО.

От ЛПЭ зависит z_10n - удельная энергия, поглощённая в ОП в результате одного события.

z ,       '„ v ^x '_i;    V ^х ».                                                                                  (25)

где Е ср - средняя энергия, поглощённая в ОП; M - масса ОП ( M = п х р х L 3 /6), р =1 г/см 3 - плотность вещества в клетке; L ср – средний пробег ИЧ в ОП. В принятых предположениях распределение длин пробегов ИЧ в ОП является треугольником, поэтому    L ср =2/3 х L   [3].

B =2/3 х L / M =4/( п х р х L ²)=const и не зависит от ЛПЭ.

Если f i (е) представляется (23), то, учитывая (21):

f 2 (E)= j £ ^{м к} / 1 (t)/ i (Е - t)dt + j^ / 1 (t)f i (е - t)dt .                                     (26)

^{о                               Е Е} макс

Если взять интегралы, то получим:

f 2 (E) =

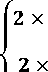
Зе ⁴

ЭЕмакс бЕмаксХЕ—Е3—4Емакс

3£ 4

^ЭЕ макс

I о

о < Е < Е макс

^Е макс <  ^Е <  ^2Е макс

Е < 0; Е>2Е макс

Биологические параметры модели (вероятности повреждения ЧО). В предлагаемой модели основной биологической характеристикой является функция ϕ ( ε ) , которая задаёт чувствительность клетки к облучению. Предполагается, что она обладает следующими свойствами:

^ (0)=0; ^ (”)=1; ф ( е ) - возрастающая функция.

Чтобы определить вид функции ф ( е ) , используется зависимость ОБЭ от ЛПЭ - линейной потери энергии ИЧ. ОБЭ определяется из равенства вероятности эффектов:

n (D i ) = n D) ,

где Di - доза образцового излучения, приводящая к заданному эффекту; Dx - доза произвольно заданного излучения, приводящая к этому же эффекту. Индекс 1 относится к образцовому, а x - исследуемому излучению.

По определению ОБЭ = D i /D x . В рамках LQ-модели:

ОБЭ = 2а2х

xD i /

(J ^a ix + ^4а 2х х (ап х D 1 + а_м х D²)

—

ап) .

Если а 2x =0, то:

ОБЭ = a ix /(a ii + a₂₂xD i ) ,                                                                  (30)

где a ii , a 2i - параметры образцового излучения; a ix , а 2х - параметры исследуемого излучения.

Из радиобиологических экспериментов известно, что зависимость ««ОБЭ - ЛПЭ» для гибели клеток имеет максимум при известном значении ЛПЭ м . Также из экспериментов известно, что для тяжёлых заряженных частиц, имеющих ЛПЭ, близкую к ЛПЭ м , а 2 =0. Отсюда следует, что ОБЭ представляется выражением (30). В этом выражении член ( а 11 +а 22 × D 1 ) задаёт уровень эффекта (значение вероятности гибели клеток).

В работе рассматривается 3 варианта модельных функций: пороговая, кусочно-линейная и линейно-квадратичная. Оценка вариантов проводилась по дополнительному критерию наличия в расчётной зависимости «ОБЭ - ЛПЭ» максимума.

Первый вариант: ф ( е ) - пороговая функция ( е о - порог), т.е.:

^(е)^1’    £^£°

(°’      е < е°                                                                                   ''

Учитывая (12) и (18), получим, что:

S   рак^ (е)йе = 1— -^-=1 — Етг.(32)

• 1    j°0                           Е^акс

В рамках сделанных предположений с учётом (19), (23) зависимость ОБЭ от у (ЛПЭ) будет:

ОБЭ = С х at = CxKl^L = ^1xj1— Д).(33)

1             1 Х1ОП    у/

Для первого варианта параметрами модели будут: L - размер ОП; l - размер ЧО; C i =const

• - не зависит от y .

Из радиобиологических экспериментов [5, 10-12] известно, что для кривых выживаемости клеток Т1 почки человека ОБЭ имеет максимум по ЛПЭ при у т =110 кэВ/мкм. Чтобы найти Ь= е о /1 , продифференцируем (33) по у , приравняем производную dОБЭ/dy при у = у т к нулю и получим, что b = у т / V3 = 70 кэВ/мкм.

Отсюда следует, что в принятых предположениях вариант 1 может быть использован только для ИЧ с ЛПЭ>70 кэВ/мкм, т.к. при меньших ЛПЭ ОБЭ будет отрицательным. Это противоречит имеющимся экспериментальным данным. Следует отметить, что максимум зависимости ОБЭ от ЛПЭ для пороговой функции ф ( е ) существует.

Второй вариант: ф ( е ) - кусочно-линейная функция,

Р(е") = 1 - ехр(-Ь х е) = 1 - ехр(-° х ху),(34)

где 0< x < l .

Подставив (23) и (34) в (20), и учитывая, что A =2/ Е ма _кс , получим:

S₁ = /^Емакс А х е(1 - ехр(-Ь х е))^е = 1 - А /^Емакс е х ехр(-° х е) ^е =

= 1 -  2 Л +    --7 х ехР(-Ь х Емакс) +  2 Л х ехР(-° х Емакс)

(° ^хЕ макс )     ⁽ ° ^хЕ макс )                              (° ^хЕ макс )

Учитывая, что £ макс =у х l и 0 =b х l , получим зависимость S 1 от у=ЛПЭ:

2         22

• ^S 1 = ^1- (д т ху) + их?) ^{х ехр(-} ^ ^{х у) +} (^ху) ^{х ехр(-} ^ ^{х у);}

S1

ОБЭ = К х =-!- = z1Qn (12   22

• ; - XX?+    х ехр(-д х у) + XX5 х ехр(-д х у)).

Чтобы найти в , продифференцируем (36) по у , приравняем производную dОБЭ/dy при у = у т к нулю и получим уравнение (37), из которого найдём значение искомого параметра в .

t2 х (1+2exp(-t))+6tx exp(-t) = 6 х (1-exp(-t)),(37)

где t= ex у т .

Уравнение (30) имеет только один корень t =0. Это возможно только при 0 =0. Таким образом, для данного вида функции ф ( е ) максимум зависимости ОБЭ от ЛПЭ отсутствует. Этот результат противоречит имеющимся радиобиологическим данным, поэтому данный вариант не может быть использован в предлагаемой модели.

Третий вариант:

Ф ( е ) = 1-exp(-b i x£ -b 2 * £ ²) = 1-exp(- 0 1 х у- 0 2 х у²) .                                        (38)

В этом варианте в функции ф ( е ) введён линейный член и появился ещё один параметр в 1 . В данном варианте не удаётся получить аналитическую зависимость ОБЭ от ЛПЭ. Модельные расчёты показали существование максимума ОБЭ от ЛПЭ. В этом варианте значения в 1 и 0 2 считаются свободными параметрами. Следует отметить, что S 1 и S 2 не зависят от размеров ЧО.

Данный вариант использован для расчёта теоретических зависимостей вероятности гибели клеток от дозы для ИЧ с разной ЛПЭ и сравнения их с экспериментальными зависимостями.

Анализ вариантов требует введения ещё одного условия: функция ф ( е ) должна иметь порог или по крайней мере квазипорог. Это требование может быть важным при экстраполяции вероятности возникновения радиационно-индуцированных эффектов в область малых доз облучения.

Значения свободных параметров модели

Для поиска значений свободных параметров в работе в качестве радиационно-индуцированного эффекта рассматриваются вероятности гибели клеток Т1 почки человека в зависимости от дозы n (D) при облучении их однократно и мгновенно ионизирующими частицами с разными ЛПЭ. Выбор эффекта и вида клеток обусловлен наличием достаточного количества экспериментальных данных, представленных в [5, 10-21]. Обработанные экспериментальные радиобиологические данные взяты из [5].

Для расчёта а 1 и а 2 предлагаемой модели необходимо найти значения свободных параметров L , K 1 , r , β 1 и β 2 для конкретных данных. Формально задача определения параметров ставится следующим образом:

• -    имеются функции η экс i (D) , полученные в результате радиобиологических экспериментов ( i =1, 2, …, n – число экспериментов) для ИЧ с заданным ЛПЭ;

• -    функция η расч (D) определяется на основе расчётов по предлагаемой модели с заданными значениями свободных параметров;

• -    оптимальные значения параметров определяются из условия, чтобы

Л = £ . £_О|П экс. (О)-П расчИ .                                                      (39)

было минимальным.

Предполагается, что значимость (вес) всех экспериментальных данных одинакова, независимо от дозы и качества излучения. В качестве базового набора использовались экспериментальные данные, представленные в табл. 1.

Таблица 1

Значения относительного отклонения значений вероятности гибели клеток Т1 почки человека, полученные в разных экспериментах [5, 15-21], при разных дозах (0,1-5 Гр)

Излучение	ЛПЭ, кэВ/мкм	Эксперимент		Образцовая функция		D , Гр
		а 1 , Гр-1	а 2 , Гр-2	а 1 , Гр-1	а 2 , Гр-2	0,1	1	2	5
Х, 250кэВ 9	2	0,126	0,066	0,22	0,049	0,69	0,35	0,17	0,01
Х, 250кэВ 8	2	0,213	0,0361	0,22	0,049	0,04	0,07	0,08	0,05
Х, 250кэВ 7	2	0,293	0,067	0,22	0,049	0,25	0,22	0,18	0,06
Х, 250кэВ 6	2	0,22	0,0493	0,22	0,049	0	0	0	0
Х, 250кэВ 5	2	0,215	0,0325	0,22	0,049	0,03	0,08	0,10	0,06
Х, 250кэВ 4	2	0,278	0,0405	0,22	0,049	0,20	0,13	0,08	0,01
Х, 250кэВ 3	2	0,172	0,043	0,22	0,049	0,27	0,22	0,17	0,06
Х, 250кэВ 2	2	0,204	0,0304	0,22	0,049	0,09	0,13	0,15	0,09

В результате решения поставленной задачи (минимум H ) для варианта 3 получены следующие значения параметров модели вероятности гибели клеток Т1 почки человека: L =5,4 мкм; К 1 =1,8; r =0,001; β 1 =0,0012 мкм/кэВ; β 2 =0,00012 мкм²/кэВ².

Результаты и обсуждение

Для обоснования модели использовались классические радиобиологические данные по вероятности гибели клеток Т1 почки человека, лежащие в основе рекомендаций МАГАТЭ по определению ОБЭ ИИ разного качества. В работе представлены результаты расчётов по предлагаемой модели и их сравнение с экспериментальными данными, полученными различными радиобиологическими лабораториями.

В качестве предлагаемой используется LQ-модель с параметрами а 1 и а 2 , определяемыми выражениями (18) и (19). Расчёт значений S 1 и S 2 проводится с использованием:

• -    функций f 1 ( ε ) и f 2 ( ε ) , задаваемых (22, 23) и (26, 27);

• -    представления ϕ ( ε ) (38);

• -    следующими значениями параметров L =5,4 мкм; К 1 =1,8; r =0,001; β 1 =0,0012 мкм/кэВ; β 2 =0,00012 мкм²/кэВ².

В данной работе в качестве критерия для сопоставления расчётных и экспериментальных данных используются значения относительного отклонения ( P ).

Р = |П экс (О,У) - П расч (О,У)|/П экс ⁽ О,У) ,                                                   (40)

где п экс (О,У) и П расч (О,у) — результаты радиобиологических экспериментов и расчётов, у =ЛПЭ.

Результаты расчётов и их сопоставление с экспериментальными данными представлены в табл. 2 и 3 и на рис. 1. Максимальное относительное отклонение (40) расчётных кривых вероятности гибели клеток Т1 почки человека от экспериментальных при дозах выше 0,1 Гр и ЛПЭ выше 2 кэВ/мкм до 200 кэВ/мкм не превышает 32%. Максимум ОБЭ достигается при ЛПЭ, равном 123 кэВ/мкм.

Таблица 2 Тест 1. Экспериментальные [5, 10-12] и расчётные значения параметров LQ-модели и максимальное относительное отклонение (40) при различных дозах

Излучение	ЛПЭ, кэВ/мкм	Эксперимент		Расчёт		D , Гр
		a i , Гр-1	а г , Гр-2	a i , Гр-1	а г , Гр-2	0,1	1	2	5
Х, 250кэВ	2	0,210	0,030	0,243	0,023	0,15	0,09	0,05	0,00
Х, 200кэВ	2,5	0,25	0,030	0,251	0,019	0,00	0,03	0,05	0,05
d,14,9МэВ	5,6	0,30	0,040	0,300	0,012	0,01	0,07	0,10	0,09
d, 6,3 МэВ	11	0,315	0,053	0,384	0,009	0,20	0,06	0,03	0,07
d, 3,5 МэВ	17,4	0,36	0,043	0,480	0,008	0,31	0,16	0,07	0,02
Не-4, 26,8 МэВ	24,6	0,43	0,086	0,584	0,007	0,32	0,11	0,00	0,03
Li	55	0,80	0,015	0,948	0,004	0,17	0,10	0,05	0,005
Не-4, 8,3 МэВ	60,8	1,00	0,069	1,000	0,004	0,01	0,04	0,03	0,005
Не-4, 5,2 МэВ	85,8	1,57	0,008	1,162	0,002	0,25	0,13	0,06	0,003
He-4, 4,0 МэВ	110	1,75	0,000	1,228	0,001	0,28	0,14	0,06	0,002
Не-4, 3,6 МэВ	123	1,56	0,000	1,234	0,001	0,20	0,10	0,04	0,002
Не-4, 3,1 МэВ	141	1,60	0,000	1,218	0,001	0,22	0,12	0,05	0,002
Не-4, 2,5 МэВ	166	1,50	0,000	1,165	0,000	0,21	0,11	0,05	0,002
Не-4, 1,8 МэВ	200	1,00	0,000	1,067	0,000	0,06	0,04	0,02	0,002

В набор экспериментальных данных Тест 2 [5, 13, 14] вошли эксперименты с теми же ионизирующими частицами (фотоны, дейтоны, α -частицы), что и для Теста 1. Из 10 экспериментов относительное отклонение (P) более 30% наблюдалось в 3 экспериментах (Х, 50 кэВ 1, d, 14,9 МэВ, Не-4, 26,8 МэВ) (табл. 3).

Таблица 3

Тест 2. Экспериментальные [5, 13, 14] и расчётные значения параметров LQ-модели и максимальное относительное отклонение (40) при различных дозах

Излучение	ЛПЭ, кэВ/мкм	Эксперимент		Расчёт		D , Гр
		a i , Гр-1	а г , Гр-2	a i , Гр-1	а г , Гр-2	0,1	1	2	5
Х, 250кэВ	2	0,21	0,03	0,243	0,023	0,15	0,09	0,05	0,00
Х, 50кэВ 1	4,5	0,175	0,046	0,283	0,014	0,57	0,29	0,11	0,05
Х, 50кэВ 2	4,5	0,212	0,036	0,283	0,014	0,31	0,17	0,07	0,04
d, 14,9 МэВ	5,6	0,2	0,039	0,300	0,012	0,47	0,26	0,12	0,03
d, 3,0 МэВ	20	0,51	0,014	0,519	0,008	0,02	0,00	0,00	0,01
Не-4, 26,8 МэВ	24,5	0,382	0,02	0,583	0,007	0,51	0,35	0,22	0,05
Не-4, 8,3 МэВ	61	1,04	0,03	1,002	0,004	0,04	0,03	0,02	0,003
Не-4, 5,1 МэВ	85	1,24	0,069	1,158	0,002	0,07	0,06	0,04	0,003
Не-4, 4,0 МэВ	110	1,74	0,008	1,228	0,001	0,28	0,14	0,06	0,002
Не-4, Ро-210	140	1,5	0	1,219	0,001	0,18	0,09	0,04	0,002
Не-4, 2,5 МэВ	166	1,5	0	1,165	0	0,21	0,11	0,05	0,002

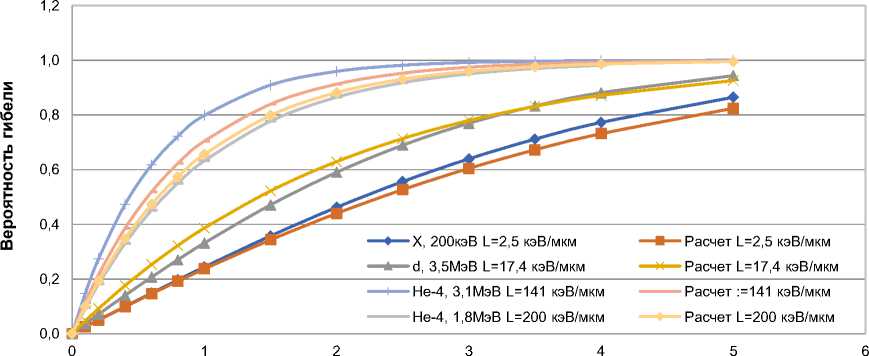
Доза, Гр

Рис. 1. Экспериментальные и расчётные кривые вероятности гибели клеток Т1 почки человека в зависимости от дозы при облучении их ионизирующими частицами с разными ЛПЭ (L, кэВ/мкм). Тест 1. Набор экспериментов [5, 10-12].

Из представленных результатов можно сделать вывод, что предлагаемая модель хорошо описывает тестовый набор экспериментальных данных.

Таким образом, удалось подтвердить правильность представлений о процессах поражения и гибели клеток. Предложенная модель может быть использована для решения широкого круга задач количественной оценки вероятности выхода радиационно-индуцированных эффектов. Например, модель может быть использована для оценки биологического эффекта при облучении клеток частицами, имеющими разные ЛПЭ, в частности, при гамма-захватной лучевой терапии. При этом используются свойства модели, которые следуют из того, что биологические параметры модели не зависят от ЛПЭ.

Подходы, использованные при разработке предложенной модели, могут быть использованы для оценки биологического эффекта при длительном, например, фракционированном облучении.

В основе модели лежит и считается доказанным утверждение, что вероятность выхода эффекта однозначно связана с числом повреждений в клетке. Для того, чтобы учесть репарационные процессы при длительном облучении, в модель можно и достаточно ввести изменение числа повреждений во времени.

Выводы

В рамках реализации концепции «идеальной» радиобиологической модели предложена модель, позволяющая проводить расчёты вероятности гибели клеток при облучении их ионизирующими частицами с разными ЛПЭ, используя радиобиологические экспериментальные данные при облучении клетки млекопитающих ионизирующими частицами с одной ЛПЭ.

На примере экспериментальных данных по облучению клеток Т1 почки человека в данной работе показано, что разработанная модель позволяет рассчитать вероятность гибели клеток в зависимости от дозы ИИ с произвольно заданными ЛПЭ для фотонов, электронов, α -частиц с ЛПЭ от 0,4 до 200 кэВ/мкм. Из представленных результатов можно сделать вывод, что предлагаемая модель хорошо описывает тестовый набор экспериментальных данных.

С формальной точки зрения предложенная модель устанавливает способ определения параметров LQ-модели и таким образом является её развитием. В предложенной модели удалось разделить биологические параметры, ответственные за появление радиационно-индуцированного эффекта, от радиационных характеристик условий облучения. Таким образом, косвенно удалось подтвердить правильность представлений о процессах поражения и гибели в данном случае клеток млекопитающих.

Из предложенной модели следует, что линейно-квадратичная зависимость вероятности гибели клеток млекопитающих может возникать не только при повреждении ДНК, но и других биологически важных молекул. При этом квадратичная зависимость эффекта от дозы объясняется особенностями поражения клетки: для повреждения некоторых биологически важных молекул (не обязательно ДНК) требуется попадания в неё двух частиц.

Рассмотрение зависимости вероятности повреждения чувствительных объёмов в предложенной модели показало возможность анализа вероятности появления радиационно-индуцированных эффектов при малых дозах. Использование данной модели может быть расширено для прогнозирования не только вероятности гибели клеток, но и для других радиационно-индуцированных эффектов, а также вероятности возникновения радиационно-индуцированных эффектов при различных временных режимах облучения.

Предлагаемая модель может быть использована при выборе оптимальных курсов нейтрон-и фотон-захватной лучевой терапии.