Радиолиния управления, работающая с ЧМ-АМ-ФТ сигналами
Автор: Ашимов Наиль Мударисович, Синицын Роман Владимирович, Апарина Юлия Петровна, Бирюков Андрей Николаевич
Журнал: Спецтехника и связь @st-s
Статья в выпуске: 2, 2011 года.
Бесплатный доступ
Рассматривается помехоустойчивость и помехозащищенность системы, в которой широкополосный сигнал формируется путем широкополосной частотной модуляции, а двоичный сигнал передается на поднесущей путем амплитудной модуляции
Широкополосная частотная модуляция, широкополосный сигнал, фазоманипулированный сигнал
Короткий адрес: https://sciup.org/14967025
IDR: 14967025
Текст научной статьи Радиолиния управления, работающая с ЧМ-АМ-ФТ сигналами
Ш ирокополосные сигналы (ШПС) представляют большой интерес для применения в радиотехнических системах (РТС) передачи дискретных сообщений благодаря ряду преимуществ, которыми они владеют по сравнению с узкополосными сигналами. Широкополосными принято считать сигналы, база которых превышает 50…100. Под базой сигнала понимается отношение ширины спектра радиосигнала к ширине спектра видеосигнала, содержащего передаваемую информацию, B = Δf / ΔF .
Отметим следующие два преимущества ШПС:
-
1) ШПС способны противостоять мощным преднамеренным (специально организованным) помехам, создаваемым в целях радиоэлектронного подавления сигналов;
-
2) ШПС имеют повышенную скрытность благодаря распределению мощности сигнала в широкой полосе частот, равной ширине спектра ШПС.
ШПС целесообразно применять в условиях активного ведения радиоэлектронной борьбы (РЭБ), когда имеет место фактически дуэльная ситуация «постановщик помех - РТС», и известна (задана) мощность преднамеренных помех. Узкополосные же сигналы следует применять, когда известна (задана) спектральная плотность мощности (напряжения) помех.
Существуют различные способы формирования ШПС. В данной работе рассматриваются РТС, работающие с дво- ичными фазоманипулированными сигналами, в которых широкополосность и необходимая величина базы ШПС достигаются благодаря использованию широкополосной частотной модуляции (ЧМ). Двоичная информация содержится в поднесущей, в которой ЧМ-колебания модулируются по амплитуде. Таким образом, в данном случае мы имеем дело с колебаниями, модулированными как по частоте с большим индексом модуляции, так и по амплитуде.
Структурная схема приема и обработки сигнала приводится на рис. 1 .
Схема содержит полосовой фильтр Ф, квадратичный детектор огибающей КД, полосовой фильтр Ф1 и далее демодек ДМ (демодулятор плюс декодер фазоманипулированного сигнала).
Структурная схема демодека ДМ представлена на рис. 2 .

Рис. 1. Структурная схема приема и обработки сигнала


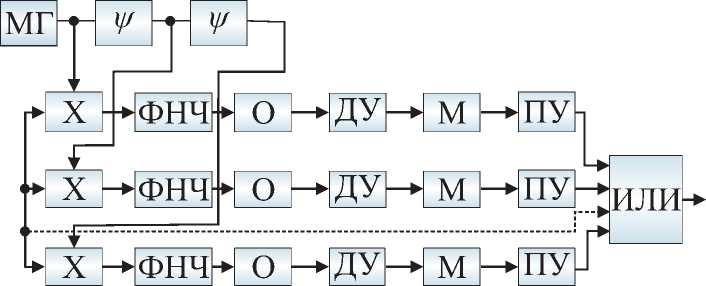
Рис. 2. Структурная схема демодека
Схема содержит N каналов приема и обработки, в каждом из которых имеется перемножитель сигналов X, фильтр нижних частот ФНЧ, двухсторонний ограничитель, декодирующее устройство ДУ, вычислитель модуля М и пороговое устройство ПУ, а также местный генератор МГ, блок фазовращателей Ψ и элемент логического сложения «ИЛИ», которые являются общими для всех каналов.
Полосовой фильтр Ф настроен на среднюю частоту принимаемого ШПС. Полоса пропускания фильтра Ф, амплитудно-частотная характеристика (АЧХ) которого близка по форме к прямоугольной, практически совпадает по величине с шириной спектра Δf ШПС. На выходе квадратичного детектора КД выделяется огибающая АМ-сигнала. Полосовой фильтр Ф1 настроен на частоту поднесущей и согласован с символом ФМ-сигнала.
Местный генератор МГ вырабатывает колебания, совпадающие по частоте с поднесущей или близкие к ней. Колебания местного генератора поступают на соответствующие входы перемножителей сигналов со сдвигом по фазе, равным 2π/N , где N – число каналов.
На практике можно обходиться тремя – четырьмя каналами, при этом достигается достоверность приема n -разрядного двоичного сигнала, соответствующая когерентному приему ФМ-сигнала с известной начальной фазой.
Ограничитель О выполняет роль решающего элемента при приеме символов двоичной комбинации и является признаком поэлементной обработки сигнала. Вычислитель модуля М служит для устранения многозначности (двузначности) входного ФМ-сигнала. Пороговое устройство ПУ выполняет роль решающего элемента при приеме всей двоичной комбинации. Сигнал на выходе порогового устройства возникает, если правильно приняты не менее n – s символов из n , т.е. допускается не более s ошибок в приеме символов двоичной комбинации. Сигнал на выходе схемы появляется, если он принят хотя бы в одном из каналов.
Предполагается, что на входе схемы действует сумма широкополосного сигнала
8(0 = У,Л1>СО^О)01 + ф(^
и белого шума. На выходе полосового фильтра Ф будем иметь сумму того же сигнала и узкополосного шума
.xU) = A(f) • cos 69О/ - В^ ■ sin aot.
Здесь ϕ(t) – мгновенная фаза, формирующая широкополосный сигнал, A(t) и B(t) – низкочастотные шумовые процессы с нулевой средней и нормальным распределением. Мощность их по величине совпадает с мощностью узкополосного шума
A4tVB4t^x4tVo".
Амплитудно-модулированные колебания описываются выражением s^f) = Ут^1 + М • cos Q?) ■ cos [®/ + <р(0], (1)
где M – коэффициент (глубина) модуляции, Ω - частота поднесущей.
Для того чтобы исключить влияние пик-фактора на достоверность приема сигнала и помехоустойчивость, примем
5(0 = y^^-(7 + M -cosQz)-cos[cof/ + ^(0]. (2)
Далее принимается М = 1,0 , следовательно, имеем
SV) = -^(V + cosQz) -cos[tt>0Z + (p(0]. (3)
На выходе квадратичного детектора получаем
Z(0 = [5(0 + x(0]‘ = 52 (/ ) + 2 • 5(0 • x(0 + X2 (0-
Первый член этого выражения образует СС-составляющую, полученную путем взаимодействия сигнала с самим с собой в квадратичном детекторе, второй член дает СХ-составля-ющую, образованную взаимодействием сигнала с шумом, третий член соответствует ХХ-составляющей, образованной взаимодействием шума с самим с собой. Выражение для СС-составляющей на выходе квадратичного детектора и на выходе полосового фильтра Ф1 после отбрасывания высокочастотных составляющих имеет вид

s"(0 = ^--cos£lt, (4)
а для СХ- и ХХ-составляющих на выходе квадратичного детектора огибающей соответственно получаем
2 • s(t) • x(t) = Vm • (7 + cosQz) • ×
× [ Л(0 cos
sin (/)],
(5)
x40-A2(0 + B2(ty Мощность сигнала на выходе фильтра Ф1 будет равна p = —— c 8 " Определим суммарную мощность СХ- и ХХ-составляющих шума в полосе фильтра Ф1. С этой целью вначале определим автокорреляционные функции с СХ- и ХХ-составляющими шума на выходе квадратичного детектора и по формуле Ви-нера-Хинчина найдем спектральные плотности шума на частоте поднесущей и мощность шума в полосе фильтра Ф1. Автокорреляционная функция (АКФ) СХ-составляющей шума на выходе квадратичного детектора описывается выражением Поскольку полоса пропускания фильтра Ф1, согласованного с символом двоичного сигнала, во много раз меньше полосы пропускания фильтра Ф (ширины спектра ШПС), мощность шума в полосе фильтра Ф1 можно определить по упрощенной формуле cy;.=^Q).A/, = V’5^ , (11)
где
m = Δf /Δf1
- отношение полос пропускания фильтров Ф и Ф1.
Спектральная плотность мощности ХХ-составляющей шума на выходе квадратичного детектора определяется выражением ~ sin2 £2 ^/
Wxx (co) = 16
• <74 f------
°-—г
cos
coOdO.
- («»%)
На частоте
ω = Ω = Ω0 /4
имеем
W(£l) =
-----. (12)
Мощность ХХ-составляющей шума в полосе фильтра Ф1 бу- дет равна -, 6-a4 =---- m.
ВсДО) = У^2 + ^0>В2(О\
(7)
Определим отношение сигнал/шум (с/ш) в полосе фильтра Ф1
где
R(θ)
- АКФ процесса
A(t)
или
B(t)
. Здесь имеется в виду, что спектр ШПС и АЧХ фильтра Ф прямоугольной формы. Следовательно, имеем
4i2 = qA • m}
^+^i
ISq^n’
где
4x=KI2^
тра Ф.
- отношение сигнал/шум в полосе филь-
где
Ω0 = 2π·Δf
- ширина спектра ШПС,
σ2
- мощность шума в полосе фильтра Ф.
Автокорреляционная функция ХХ-составляющей шума на выходе квадратичного детектора равна RJ6^4-R2(0y Спектральная плотность мощности СХ-составляющей шума в соответствии с формулой Винера-Хинчина определяется выражением
Вычислив интегралы и приняв
ω=
Ω
=
Ω
0 /4
, получаем
Wcx(^ = 4,5-V2-a2 JI ^^. ^-^^1
Рассматривается РТС, в которой факт посылки сигнала на приемной стороне заранее неизвестен и в которой применяется статистический критерий оптимального обнаружения – критерий Неймана-Пирсона, а приемно-декодирующая аппаратура не обслуживается человеком и работает автоматически. В соответствии с критерием Неймана-Пирсона вначале обеспечивается заданная и достаточная малая вероятность ложного приема сигнала
Рл = const
, а затем принимаются все меры для получения максимальной вероятности правильного приема сигнала
Рк = max
.
Помехоустойчивость широкополосной РТС будем оценивать по величине коэффициента помехоустойчивости
Кпу
, за который принимается отношение напряжения помехи
Vп
, взятой в полосе 1 кГц, к напряжению сигнала
Vc
на входе приемника, соответствующее вероятности
Рк = 0,5
. Коэффициент определяется при условии непревышения вероятности ложного приема заданной величины
Рл
за промежуток времени, равный
Та
.
За коэффициент помехозащищенности
Кпз
принимается то же отношение
Vn / Vc
, при котором
Рк = 0,5
, но напряжение помехи берется не в полосе 1 кГц, а в полосе фильтра Ф, равной ширине спектра ШПС. Следовательно, коэффициент помехозащищенности будет связан с коэффициентом помехоустойчивости соотношением
где
Δf
– ширина спектра ШПС в кГц.
Число ошибок в приеме символов двоичной комбинации, как случайная величина, имеет биномиальное распределение р^с^рги-р)5. Положив в (20) Рк = 0,5, приходим к выражению для вероят- ности правильного приема символа где Рэ – вероятность правильного приема символа двоичной комбинации, - число сочетаний из n по s, равное п\ s !• (/7 — 5)! В нашем примере имеем
Р
э
= 0,707
.
Вероятность ложного приема сигнала определяется по фор- муле где s – допустимое число ошибок в приеме символов, при котором еще обеспечивается заданная вероятность ложно- го приема сигналов. При достаточно большой разрядности кода можно перейти от дискретного биномиального распределения к непрерыв- ному гауссовскому (нормальному) распределению. Воспользуемся такой возможностью и применив метод нормального приближения по формуле Муавра-Лапласа получим
В схеме
рис. 1
прием фазоманипулированного сигнала на поднесущей частоте может быть назван псевдокогерент-ным, т.к. в ней достигается практически такой же результат, как и при когерентном приеме. Следовательно, имеем
РЭ=Ф(Я1-^,
В нашем примере получаем
q1
= 0,385.
Вернемся к формуле (14), которая приводится к биквадратному уравнению т, • q4 —18 • q] • q2 —12 • q2 = 0, где Ф(х) – интеграл вероятности Лапласа, равный решив которое получаем Р„ ^к т
Здесь
Tk = n·Tэ
- длительность
n-
разрядного двоичного сиг-
m. нала. Из (16) следует JnF(l-P)2
где
F(x)
– функция, обратная интегралу вероятности Лапласа.
Рассмотрим конкретный пример и определим показатели помехоустойчивости и помехозащищенности при следующих исходных данных:
♦
заданная вероятность ложного приема сигнала
Р
л
= 10
5
за время
Та = 8,64·105
с;
♦
разрядность кода
n = 256
;
♦
скорость передачи двоичной информации
С
=
100
бит/с;
♦
длительность
n
-разрядного двоичного сигнала
Т
к
= 2,56
с;
♦
ширина спектра ШПС
Af
=
120
кГц;
♦
отношение полос пропускания фильтров Ф и Ф1
m
1
= 1200
.
В нашем примере, пользуясь соотношением Милса, имеем
F(1 – P) = 6,6
.
Тогда, в соответствии с (18), получим
s
=
75
.
Вероятность правильного приема
n
-разрядного двоичного сигнала определяется выражением
2=0 По формуле Муавра-Лапласа имеем
В нашем примере
m1
= 1200,
q1
= 0,385. В соответствии с (23) отношение сигнал /шум в полосе фильтра Ф будет равно
q
= 0,199.
Коэффициент помехоустойчивости системы определяется по формуле где полоса пропускания фильтра Ф берется в кГц. Для при- веденных выше исходных данных в нашем примере получаем Kny = 0,458.
Коэффициент помехозащищенности определим по формуле (14)
K
nз
=
5,017
.
Радиотехнические системы, работающие с широкополосными сигналами, по уровню обработки ШПС можно разбить на три категории:
♦
РТС, которые работают с широкополосными фазомани-пулированными сигналами и в которых осуществляется когерентный (квазикогерентный) прием радиосигнала или прием на полосовой согласованный фильтр с последующим додетекторным декодированием;
♦
РТС, в которых осуществляется согласованная додетек-торная фильтрация ШПС;
♦
РТС, в которых согласованная фильтрация осуществляется после детектирования ШПС.
В РТС первой категории приемник представляет собой линейное устройство, и в нем отсутствует подавление сигна- ла помехой. Поэтому в РТС первой категории достигаются максимально возможные уровни помехоустойчивости и помехозащищенности. Однако для этого требуется высокая стабильность частоты радиосигнала и чрезвычайно высокое быстродействие цифровых устройств обработки ШПС, которые на практике не всегда возможно реализовать. В РТС второй категории требования, предъявляемые к стабильности частоты сигнала и быстродействию цифровых устройств обработки сигнала, существенно снижаются, но помехоустойчивость и помехозащищенность РТС второй категории будет значительно ниже.
Рассмотренная в данной работе РТС, работающая с широкополосными ЧМ-сигналами, относится к РТС третьей категории, в которой широкополосный сигнал непосредственно поступает на вход детектора. Из-за сильного подавления сигнала помехой в детекторе помехоустойчивость РТС оказывается значительно более низкой, чем при работе в тех же условиях с узкополосными сигналами. Например, РТС, работающая с узкополосными ЧТ-сигналами, при некогерентном приеме и приведенных выше исходных данных будет иметь коэффициент помехоустойчивости
Kny
=
3,0
. Ширина преднамеренной сосредоточенной помехи в этом случае будет равна
Δf1
или шире. Это означает, что коэффициент помехозащищенности будет равен коэффициенту помехоустойчивости или превышать его.
Преимущество рассмотренной РТС, прежде всего, заключается в энергетической скрытности передаваемых сигналов, что снижает вероятность самого появления преднамеренной помехи в канале связи. Поэтому она может быть рекомендована для применения в условиях, когда существует активное радиопротиводействие со стороны противника, несмотря на серьезное снижение помехоустойчивости. Другое важное достоинство рассмотренной РТС заключается в том, что она способна противостоять мощным сосредоточенным в узкой полосе частот помехам. Действительно, сосредоточенная преднамеренная помеха появится в полосе фильтра Ф1 и нарушит нормальную работу РТС только в том случае, если в полосе фильтра Ф сосредоточенной помехой будет поражена одна из составляющих АМ-сигнала. Вероятность же такого события является достаточно низкой. К отмеченному выше следует добавить то обстоятельство, что рассмотренная широкополосная система отличается простотой технической реализации и не требует больших аппаратных затрат. Требуемая стабильность частоты в данном случае определяется по формуле
А/
0,1
Jo Jo где f0 – частота поднесущей. В нашем примере f0 = 30 кГц, Тk = 2,56 с. Следовательно, получаем ^<1,3 X10"6. Jo Если каждый символ двоичной комбинации будет представлен N = 10 отсчетами, максимальная тактовая частота в цифровом декодирующем устройстве в соответс- твии с формулой fmax = N·n·C в нашем примере составит fmax = 2,56 МГц. Таким образом, требования к стабильности частоты и быстродействию цифровых устройств здесь являются весьма умеренными. Выводы
1. Широкополосные сигналы целесообразно применять, когда известна мощность помехи, т.е. когда имеет место дуэльная ситуация «постановщик помех - РТС», а узкополосные сигналы – когда известна спектральная плотность мощности помехи.
2. По уровню обработки ШПС радиотехнической системы могут быть разбиты на три категории. В РТС первой категории применяется когерентный прием или прием на ПСФ, а приемник представляет собой линейное устройство. В РТС второй категории осуществляется додетектор-ная согласованная фильтрация ШПС, в РТС третьей категории – последетекторная согласованная фильтрация.
3. Наиболее высокие показатели помехоустойчивости и помехозащищенности достигаются в РТС первой категории, а самые низкие показатели – в РТС третьей категории, к которой относится рассмотренная в данной работе РТС, работающая с широкополосными ЧМ-сигналами.
4. Недостатком данной РТС является низкая помехоустойчивость и невысокая помехозащищенность по отношению к широкополосной (заградительной) помехе.
5. Достоинство рассмотренной РТС заключается в высокой скрытности сигналов и ее способности противостоять мощной сосредоточенной в узкой полосе частот помехе, а также в сравнительной простоте технической реализации устройств формирования и обработки ШПС ■
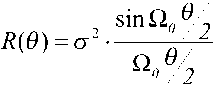
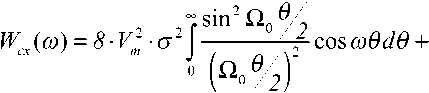
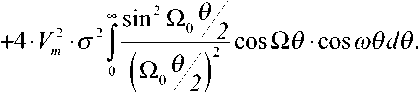
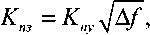

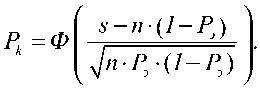
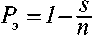
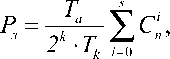
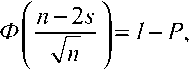
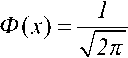
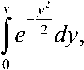
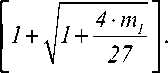
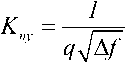
Список литературы Радиолиния управления, работающая с ЧМ-АМ-ФТ сигналами
- Шумоподобные сигналы в системах передачи информации./Под. ред. проф. В.Б. Пестрякова. М.: Сов. радио, 1973. -423 с.
- Л.Е. Варакин. Системы связи с шумоподобными сигналами. -М.: Радио и связь, 1985. -383 с.
- Справочник по теории вероятностей и математической статистике. -М.: Наука, 1985. -643 с.
- Ашимов Н.М. Помехоустойчивость и помехозащищенность радиолиний управления. М.: Изд. ВИУ, 2000. -375 с.


