Радиус кривизны Вселенной значительно меньше, чем считают астрономы

Сейчас астрономы считают, что радиус кривизны Вселенной много больше видимой Вселенной. Опираются они на некоторые наблюдения, считая их верными, и делают соответствующий вывод. Эти наблюдения зависят от модели рассматриваемой Вселенной. То есть астрономы считают, что Вселенная плоская и вводят параметры для плоской Вселенной и получают, естественно, плоскую Вселенную. Здесь я показываю, что их расчёты должны иметь на самом деле сильную зависимость от радиуса кривизны.

Для начала вспомним, что все способы измерения больших расстояний калибруется параллаксом. Даже сама единица расстояния – парсек измеряется с помощью параллакса, и название ПАРСЕК состоит из слов ПАР аллакс и СЕК унда. Поэтому все погрешности измерения на малых расстояниях связаны с погрешностями измерения с помощью параллакса, как наиболее точного на малых расстояниях. Этот вопрос специально обсуждался на «Астрофоруме» с компетентными астрономами. Они согласились, что есть много способов измерения малого расстояния, но способ параллакса наиболее точный. Точность измерения - до десятимиллионной секунды, то есть до ¹⁰ .

Сейчас астрономы придерживаются мнения, что радиус кривизны Вселенной много больше видимой части вселенной, тогда Вселенную можно считать плоской. При этом «доказывают» своё утверждение либо зависящим от модели способом измерения. То есть считают пространство плоским и вводят параметры плоского пространства и получают, естественно, плоское пространство – даже смешно. Либо доказывают, что на больших расстояниях параллаксы становятся равны нулю. Но последнее от

Доклады независимых авторов 2014 выпуск 26 непонимания неевклидовой геометрии. Для простоты рассуждения будем, например, считать геометрию Вселенной – геометрией Лобачевского.

Будем пока считать метод параллакса абсолютно точным и посмотрим, как на результат влияет кривизна пространства. И будет ли результат измерения параллаксов на больших расстояниях равен нулю при правильном измерении. Понятно, что при определении углов используются удалённые квазары. И углы оределяются относительно этих квазаров и только потом они (углы) сводятся к углам относительно плоскости орбиты. При этом плоскость орбиты - некая расчётная плоскость, так как реальная орбита только в первом приближении плоская. Но это всё трудности астрономов, которые они пока не преодолели. Нам же интересен вклад кривизны в эти погрешности, поэтому будем считать, что астрономам удалось рассчитать положение квазаров относительно плоской орбиты и соответственно получить необходимые углы относительно этой плоской орбиты.

На рис.1 две точки 1 и 2 – точки Земной орбиты. Точка 3 – исследуемая звезда. Отрезки (31) и (32) – путь световых сигналов от звезды на Землю. Считаем, что пространство искривлённое, например Лобачевского для определённости. Рассматриваем плоскость Лобачевского. Фигура, напоминающая эллипс и обозначенная W – это орицикл на плоскости, который содержит точки 1, 2, 3 и он перпендикулярен орбите Земли. Прямая (12) – прямая Лобачевского, проходящая через точки (12). Орицикл же изображает евклидову прямую на плоскости Лобачевского и тоже проходит через точки 1 и 2. Угол в точке между орициклом и световым сигналом определяют, как угол между касательной к орициклу, их две: a и b и пути световых сигналов, соответственно их два (31) и (32).

Понятно, что углы, которые измеряют астрономы, отличаются от правильных углов для параллакса, которые надо измерять. Астрономы измеряют углы между (а и прямой (13)) и (в и прямой (32)), так как считают пространство плоским, тогда они считают, что прямая, соединяющая точки 1 и 2, идёт по орициклу. А для параллакса, естественно, надо измерять углы между прямыми ((13) и (12)) и между ((32) и (12)).

Понятно, что на малых расстояниях погрешность измерения намного больше вклада в результат, получаемый от кривизны. Но на расстояниях значительных вклад от кривизны будет уже значительный, так как при удалении растёт и вклад в погрешность. И как здесь мы уже отметили: этот результат не зависит от способа измерения, так как калибровка малых расстояний проводится параллаксом, а затем эта калибровка распорстраняется на большие расстояния. То есть все большие расстояния измеренные с помощью la, или другими методами фоктически прокалиброваны с помощью параллакса и каждый парсек этого расстояния содержит погрешность от кривизны Вселенной.

Посмотрим, какую погрешность даёт кривизна.

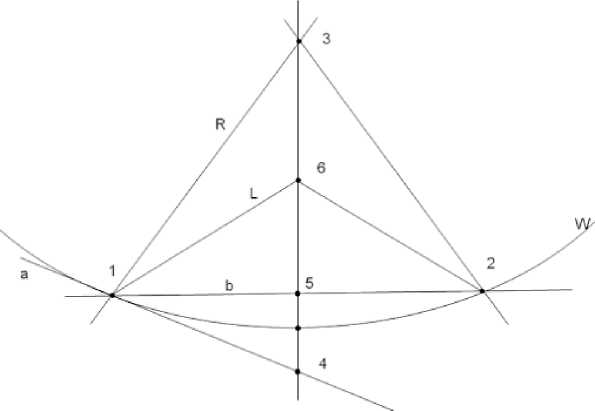
Рис. 2.

На Рис. 2. Изображена плоскость Лобачевского, точки 1 и 2 – точки Земной орбиты. Всё по-аналогии с Рис 1, кривая W – орицикл, который изображает евклидову прямую, которую астрономы считают за прямую соединяющую точки 1 и 2. Но мыто знаем, что это не так и прямая (соединяющая точки 1 и2) – это совсем другая линия. Эта прямая - a. Точка (звезда) 3 расположена на расстоянии равному радиусу кривизны Вселенной R от точки 1. Точка (звезда) 6 расположена на расстоянии в 1 парсек от точки 1. Повторяю, что считаем пока погрешность измерения =0.

Будем считать углы.

b

П _ arcsin b или угол(315)= 2 К или

• 1)    Угол (531)= ^К b

угол(514) = arcs'" К

L

arccos

• 2)    Угол (615)= ^b , угол(614)=угол(615)+угол(514), или

• L .         . b

(614)= ^arcco^s b + ^arc^sin к

• 3)    Надо найти во сколько раз увеличивается угол(615), если пространство считать плоским. То есть надо найти отношение:

b

угоЛ6140 _ t arcs'" К"=уголя^1*^

И = 1 + b

Понятно, что в первом приближении ^К , считаем удаление ^L = ¹ парсек, при этом, считая ^К = 10 пк, а ^b = 10 пк, то формула даёт погрешность ( или отличие «n» от единицы) из-за

- 14

.

кривизны примерно ¹⁰

Естественно, сравнивая эту погрешность измерения парсека, и погрешность из-за кривизны последняя считается малой. Но так же понятно, что эта погрешность для 10 Мпк будет сравнима с погрешностью измерения. А на расстоянии в 10 000 Мпк – погрешность будет очень значительная. Повторяю, что не важно, каким методом измеряли расстояние, так как калибровка проводилась параллаксом. И при этом смешно читать, что угол параллакса на больших расстояниях равен нулю. Если учитывать, что как раз на больших расстояниях увеличивается вклад от кривизны пространства Вселенной и астрономы бы не писали глупость, если бы понимали, как влияет кривизна. А на расстоянии в 4 000 Мпк – основная погрешность была бы от кривизны пространства Вселенной, если бы астрономы использовали правильные углы между плоскостью орбиты и направлением на звезду. А так как используются не верные направления (верные пока астрономы использовать не в состоянии – нехватает точности измерения), то теряется погрешность от кривизны и остаётся случайная погрешность, которая приводит к результату нулевого параллакса.

Замечу, что для расстояния равного R, от Земли, естественно, астрономы получают нулевой параллакс, так как измеряют угол между траекторией светового сигнала от исследуемой звезды и теоретически рассчитанной «прямой» геометрии Евклида (эта прямая соединяет точки на орбите Земли), которая является орициклом. Это примерно так же, как измерять угол между радиусом окружности и этой окружностью, а надо измерять угол между хордой и радиусом окружности. И понятно, что нулевые параллаксы станут совсем не нулевыми на больших расстояниях. При этом на средних расстояниях параллаксы могут быть около нуля, так как плоское пространство даёт нулевые параллаксы, а параллаксы с поправкой на кривизну тоже дают ноль, так как вклад кривизны ещё слишком мал.

Теперь, если прикинуть - какой радиус кривизны может быть у Вселенной, то получим, что может быть от 1000 до 10000 Мпк. При этом, напоминаю, другие методы зависят от рассматриваемой модели Вселенной и пытаться найти кривизну, изначально положив её равной нулю, просто глупо.