Радоновые свойства пределных множеств

Уточнённый порядок играет важную роль в теории роста субгармонических функции, в ряде других разделов математики.

Абсолютно непрерывная функция ^С’. на полуоси ^^ называется уточнённым порядком, если выполняются следующие два условия :

_ 1йпр(г:' = р(эс) = ;?е1-^л-:■

• 1)    существует предел 7—-=                       ,

hm г Ьгр'Сг :■ = о

• 2)                   .

В приложениях чаще всего используется не сам уточнённый порядок ^(■’. , а функ-ция           . Отметим следующее свойство уточнённого порядка.

Теорема 1. для любого г > С1 существует предел lira

= f

и этот предел равномерный на любом сегменте

Если ^С’. – уточнённый порядок, то существует дифференцируемый, и даже анали-тический, уточнённый порядок £ (■. такой, что

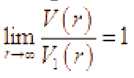
КИ=^' ' где

Поэтому предположение о дифференцируемости уточнённого порядка часто не ограничивает общности рассуждений. В дальнейшем мы будем предполагать, что функ-ция ^С’. является непрерывно дифференцируемой на полуоси .

Рост произвольной функции f(-. сравнивается с ростом функции вида РИ.

Множество функций вида – это более широкое множество, чем множество степеней ,            , или множество функций вида

A‘|>r)\hv^-4^ ГПР где

– вещественные числа, а – это -тая итерация логарифма. Например,         .

. Порядком

Пусть – положительная функция на полуоси функции называется число

р = Inn-----

,—= In г

Важность понятия уточнённого порядка в теории роста функций можно усмотреть из следующей теоремы.

Положительная на полуоси функция называется регулярно меняющейся в смысле Караматы, если для любого существует конечный предел

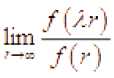
Пусть р ( t ) - некоторый уточнённый порядок. На пространстве R c определяется одно-параметрическое семейство преобразований Азарина At : R c ^ R c , t e ( 0 ,^ ), согласно формулам

р (tE)

& At^р’^рt ⁽ E ) v ( t ) ’

Для любого борелевского множества E .

Пусть ф e Ф ( R n ) . Формула переменных даёт

J ф ⁽ x ) ^dP_t ⁽ x ) = 1Д л J Ф ( x ) dP ⁽ t ) • (4-¹)

R П                         V ⁽ t ) R П t

Пусть множество ve RC:v = lim Атр, lim tm=+” будем называть m→∞     m→∞ предельным множеством Азарина для меры ри обозначим через Fr [ р ].

В случае вещественных радоновых мер наряду с предельным множеством Азарина Fr [ р ] важными асимптотическими характеристиками меры р являются её верхняя конусная плотность Д ( E ) и нижняя конусная плотность Д ( E ), а также верхняя плотность N ( а,Е ) и нижняя плотность N ( а,Е ) . Пусть r о ^{> 0} - некоторое фиксированное число, E - борелевское подмножество единичной сферы S n - 1 в пространстве R n , f ⁽ r,E ) = р ( ( r о ,r ] ^E ).

Тогда указанные высшие величины определяются следую щим образом

Д ( E ) = lim L ^{f (} r’E ) ’Д ( E ) = lim L f i r’E l ,LL r^ V ( r )    ^v         r^ V ( r )

f ( r + ar,E ) - f ( r,E )                     f ( r + ar ,E ) - f ( r ,E )

N(a,E)=lim L —----- ' ■ —-,N(a,E) = lim L —----- ' ■ —-• (4.2)ll r→ ∞                                      r→ ∞

Заметим, что величины △ ( E ) и △ ( E ) имеет смысл определить только в случае, если уточнённый порядок р ( r ) таков, что ^р = l™ ' ^{( r )> 0} . Это особенно наглядно для случая положительной меры. В случае р >0 величины А ( E ) и А ( E ) не зависят от выбора числа ^r 0 .

Заметим, что величины N ( а,Е ) и N ( а,Е ) не зависят от ^r о для любых уточнённых порядков р ( r ). Эти величины имеют смысл рассматривать для любых уточнённых поряд-ков. Эти величины являются важными характеристиками мер, как в случае р >0 , так и в случае р< 0 .

В общем случае, когда нет связи между мерой μ и уточнённым порядком р ( r ) каждая из четырёх величин является элементом расширенного множества вещественных чисел [ - ^ж,^ж ] . Обычно величины N ( а,Е ) и N ( а,Е ) рассматривают как функции на полу-оси α ≥ 0 . Однако, иногда удобно считать эти величины функциями на полуоси а >-1 .

Из свойств пределов и уточнённого порядка р (r) вытекают следующие соотношения

N ( а + в,Е ) ( a,E ) + ( 1 + а

N ( а + в,Е ) >N ( a,E ) + ( 1 + а

N ( а + в,Е ) ( a,E ) + ( 1 + а

N ( а + в,Е ) ( a,E ) + ( 1 + а

) ' ^N ( 1h’^E ) - ^{( 4}-3)

• ' N ( ih-EE K ) >  ' N ( -^-E У4-⁵ •

> ' N ( ih-E ) ’ ⁽ 4.6 •

_где р = р ⁽ ^ ) = lim р ⁽ r ) r→∞

Определение 4.1. Пусть – произвольный уточнённый порядок Обозначим через           множество мер          таких, что для некоторого для верхней плот-ности меры относительно уточнённого порядка выполняется неравенство .

Заметим, что если             , то неравенство выполняется для любого . Теперь из неравенства (4.17), применённого к мере и локальной конеч-ности этой меры следует, что неравенство

| w 11 | г, (г + а )г ] X S^ ) <  MV (Г)

с некоторой постоянной           выполняется для всех . Таким

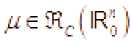
г              Mjp(H)

совпадает с множеством тех мер

образом, множес-тво для которых для любого величина

J($) = SUp конечна. Из локальной ограниченности меры “ следует такие конечность величины

^слл )= sup

^. > 0

(4.18)

при -

Определение 4.2. Пусть ^C’. – произвольный уточнённый порядок

Обозначим через M (P^)) существует a > 0 такое, что

множество мер

АбМ (p(r)i

, для которых

Напомним, что функция p определяется формулой (4.7).

состоит из

Справедливо следующее утверждение. Множество тех мерре M , для которых для любого c ■ величина

B[q )= sup конечна.

Из соотношения легко следует, что положительная полутраектория P (множество {p, .t e[L x ) является компактным множеством. Сформулируем это утверж-дение в виде отдельной леммы.

Лемма 1. Пусть pC’ . – произвольный уточнённый порядок, /zeM _B(p(r))

Тогда полутраектория P,г > 1 , есть компактное множество радоновских мер

Доказательство.

и ^^/(OH?)

Пусть 0 < ж p < ^ . Используя неравенства(4.18)

, получаем оценку

Ик*м.,) ■ *^p

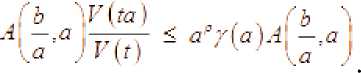
Теперь утверждение леммы следует из теоремы 3.4. Лемма доказана.

Далее наша задача состоит в описании свойств предельных множеств мер из класса м JpC’l . Вначале мы сформулируем теорему, которая позволяет свести эту задачу к более простому случаю, когда .

Теорема 2. Пусть p. ( ■’. и Pi 0’ – уточнённые порядки такие, что lim p- (r) = lim p ( r) = p             де M .

-::          -::         . Пусть ■     ~ i ж " a Mepa z определяется равенством

Тогда

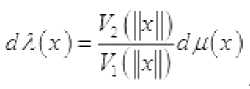
и соотношения ■ "

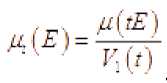
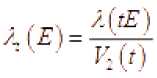
эквивалентны. Здесь

г(п=/

Доказательство. Имеем

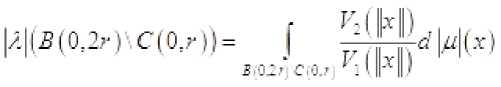
Из теоремы 2.1 легко следует, что р.||5(0:2г) CWli —ИШ2Н C(OrHi шп-----------------= lim-----------------

■'-=      ^(Н                  ^0')

Из того, в свою очередь, следует, что ze М ДлО'))

Пусть Я, 1 , (Рё Ф . Имеем

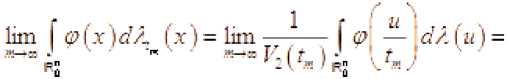
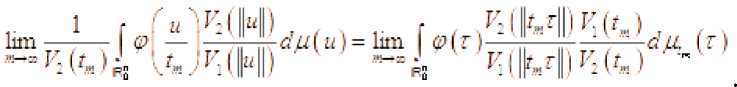
Так как последовательность

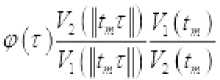
Сходится в пространстве Ф к функции ^ и ■L-    , то следует, что lim |й>(х)б'л,    = [<р(г)Л'(г)

Ж^д •        4   ‘        ГТ 4   ’       »       4   •             *

Fq                       “S                 .

Тем самым мы доказали, что ^   . В доказанном утверждении можно поменять местами и^ . Теорема доказана.

Отображение , 4а= д , в случае, когда р^-)^р мы будем обозначать или F. I j . В следующей теореме приводится ряд свойств предельного множества .

Теорема 3. Пусть ^С’. – произвольный уточнённый порядок

AGM Jp(r)i

. Тогда справедливы следующие утверждения:

• 1)    ^^г[р] есть непустой компакт,

2 [/^1                                                                                     I'^'Cs^J

• 2)    есть связное множество в метрическом пространстве ,

• 3)    множество ' [^a] инвариантно относительно преобразования , более того есть взаимно однозначное отображение множества " [^] на себя.

Доказательство. Как следует из теоремы 4.3, не ограничивая общности, можно считать, что Р1»/>. По лемме 4.5 полутраектория “: ,’ > 1 , является компактным множеством. На языке динамических систем это утверждение переформулируется так. Движение положительно устойчиво по

Л- в широкая сходимость сходимости в метрическом

Лагранжу. На компактных множествах последовательности эквивалентна пространстве совпадает с

пространстве

I9WI                             м

. Поэтому предельное множество Азарина a -предельным множеством траектории в метрическом

I JL ^ I

. Теперь мы можем использовать достаточно развитую теорию динамических систем в метрических пространствах. Теорема 10, глава 5, § 3 из книги [6] утверждает, что ^[^] есть непустой компакт, который отображение “: взаимно однозначно отображает на себя, а теорема 14 из этой книги утверждает, что ^^] есть связное множество. Теорема доказана.